大话数据结构-图的深度优先遍历和广度优先遍历
4 图的遍历
图的遍历分为深度优先遍历和广度优先遍历两种。
4.1 深度优先遍历
深度优先遍历(Depth First Search),也称为深度优先搜索,简称DFS,深度优先遍历,是指从某一个顶点开始,按照一定的规则,访问并记录下一个未访问顶点。对于非连通图,则是按连通分量,采用同一规则进行深度优先遍历的方式,以以下图为例:
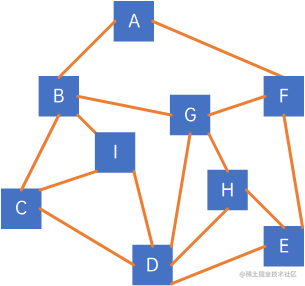
我们使用visited[vertexSize]来记录已访问的顶点,先从A开始,并把A加入到visited中,访问规则是“下一个访问的顶点是最右手边的那个顶点”,注意,图上的小人是面向我们,从上往下走的,此时visited = {A}:
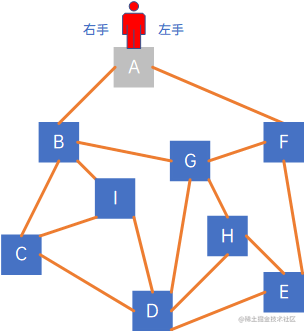
接下来,依附于顶点A的边有(A,B)、(A,F),小人右手边的边是(A,B),因此延着(A,B)走,visited = {A, B}:
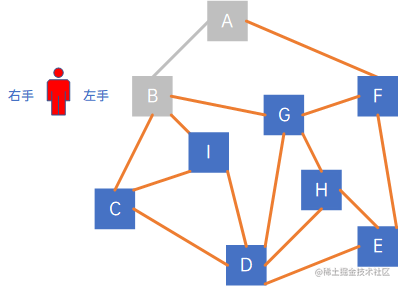
依附于顶点B的边有(B,C)、(B,I)、(B,G),小人右手边且没被走过的边是(B,C),于是延着边(B,C)走,visited = {A, B, C}:
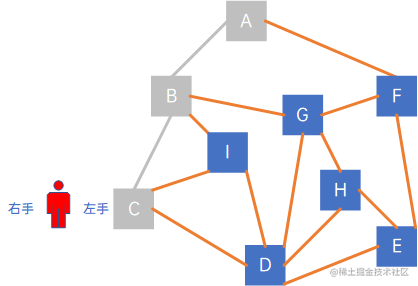
按照这个规则走,走到F时,visited = {A, B, C, D, E, F}:
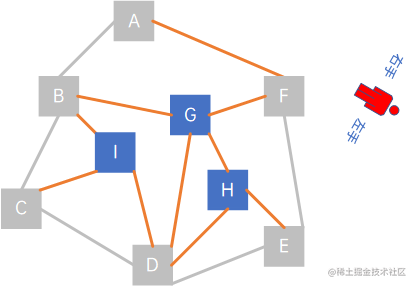
这时,小人的右手边有几条路,从右至左依次是(F,A)、(F,G)、(F、E),但顶点A在visited中,表示顶点A已经被访问过了,所以排除(F,A),延着(F,G)走,visited = {A, B, C, D, E, F, G}:
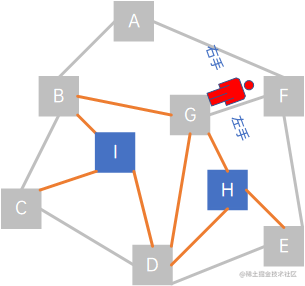
这时,相对于顶点G,小人可走的路从右到左依次是(G,B)、(G,D)、(G,H),B和D已经在visited中,因此跳过,延着(G,H)走,visited = {A, B, C, D, E, F, G, H}:
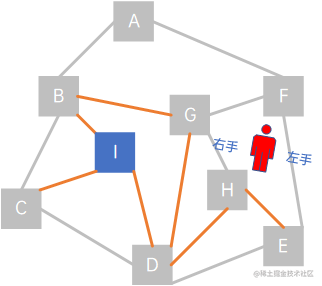
这是,相对于顶点H,小人可走的路从右到左依次是(H,D)、(H、E),但D和E都在visited中了,这时,让小人延原路返回,即延着(H,G)走:
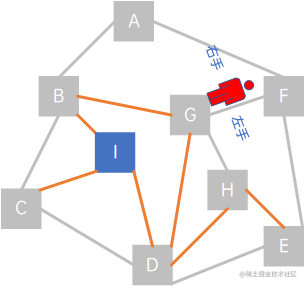
但相对于顶点G,可走的路(G,B)、(G,D)和(G,H)三条路对应的顶点B、D、H也都在visited中了,无路可走了,继续原路返回,到顶点F,仍然无路可走,继续返回E,仍无路可走,继续返回D:
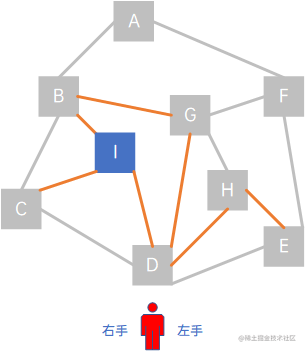
这时,发现了(D,I)这条路还没走过,于是延着(D,I)走,visited = {A, B, C, D, E, F, G, H, I}:
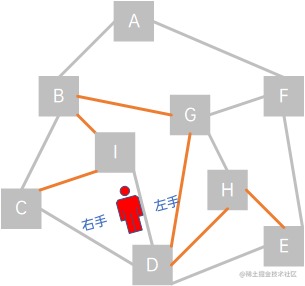
又无路可走了,于是原路返回,直到返回顶点A,也就是开始的那个顶点,表示图已遍历完。
再来总结一下深度遍历优先的过程:
(1) 先定一个规则,比如“延着依附于当前顶点中,最左侧的,未被访问的边进行迭代”;
(2) 从某一个顶点开始按定义的规则迭代;
(3) 若有符合规则的边,则继续往下迭代,若无符合规则的边,则一步一步原路返回,查找可迭代的边;
(4) 当原路返回到最开始的那个顶点时,迭代完毕;
实际上整体上是一个递归调度的过程,主要就是找到“下一条边”。
注意,深度优先遍历的规则并不是固定不变的,只要最终结果遵循“按一定规则,逐步访问结点的下一个邻边”即可。
4.1.1 邻接矩阵的深度优先遍历
我们举几个例子:
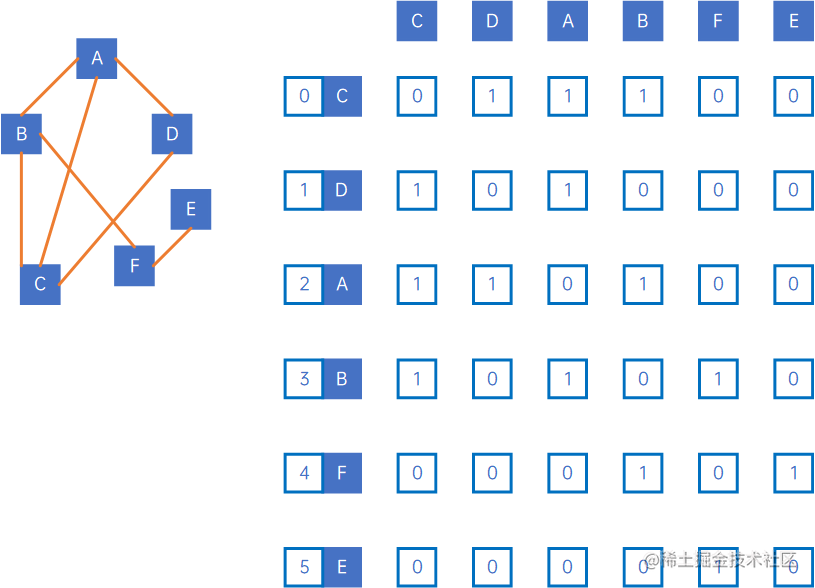
对这些图使用深度优先遍历时,找“下一条未被访问边”的方式是:
(1) 从第一个顶点开始,访问arc[0][1]、arc[0][2]…arc[0][n],找到第一个未被访问的边,边的判断是,如果为图,则值为1表示存在边,如果为网,则值不为无穷大且arc[i][j]中i不等于j表示存在边;
(2) 找到这个边后,访问它,假设这个边为arc[0][x];
(3) 然后继续访问arc[x],找到x的未被访问的边,即递归第(1)、(2)步,直到所有关联的边都访问完;
(4) 若此时,结点还未迭代完,则从第二个“未被访问的顶点”开始,继续迭代;
因此如上无向图的遍历过程如下所示:
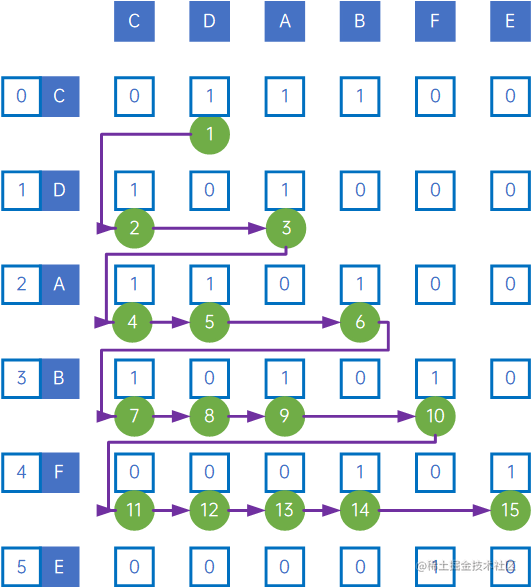
过程为:
(0) iterate C;
(1) 遍历arc[0][j],寻找C相关的顶点,找到(C,D),visit C,visit D;
(2) 遍历arc[1][j],寻找D相关的顶点,找到(D,C),两个顶点都被访问过,跳过;
(3) 找到(D,A),visit A;
(4) 遍历arc[2][j],寻找A相关的顶点,找到(A,C),两个顶点都被访问过,跳过;
(5) 找到(A,D),两个顶点都被访问过,跳过;
(6) 找到(A,B),visit B;
(7) 遍历arc[3][j],寻找B相关的顶点,找到(B,C),两个顶点都被访问过,跳过;
(8) 找到(B,D),值为0,不相关,跳过;
(9) 找到(B,A),两个顶点都被访问过,跳过;
(10) 找到(B,F),visit F;
(11) 遍历arc[4][j],寻找F相关的顶点,找到(F,C),值为0,不相关,跳过;
(12) 找到(F,D),值为0,不相关,跳过;
(13) 找到(F,A),值为0,不相关,跳过;
(14) 找到(F,B),两个顶点都被访问过,跳过;
(15) 找到(F,E),visit E,此时所有顶点均访问完毕,结束;
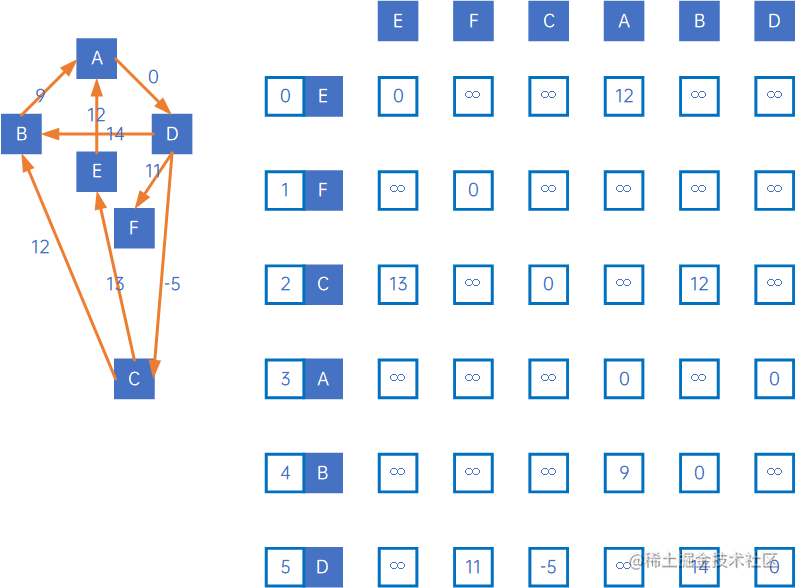
如上有向网的遍历过程如下所示:
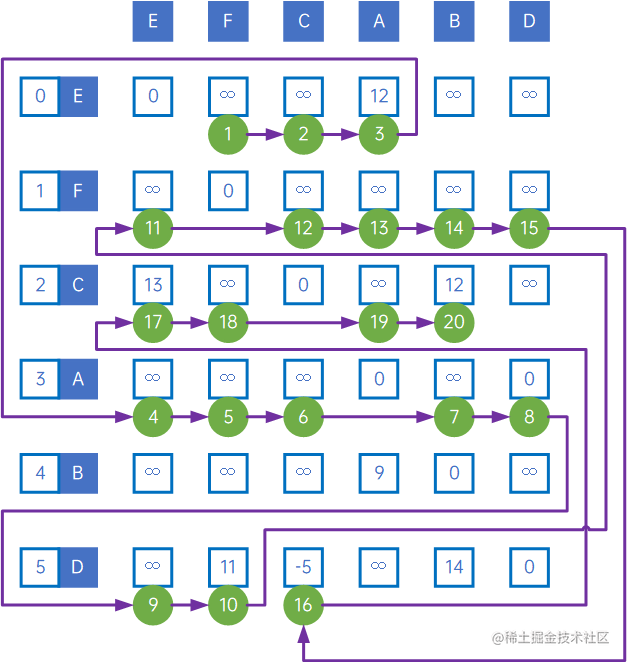
过程为:
(0) iterate E;
(1) 迭代arc[0][j],寻找E指向的顶点,找到<E,F>,visit E,然后发现数组值为无穷大,不相关,跳过;
(2) 找到<E,C>,值为无穷大,不相关,跳过;
(3) 找到<E,A>,visit A;
(4) 迭代arc[3][j],寻找A指向的顶点,找到<A,E>,值为无穷大,不相关,跳过;
(5) 找到<A,F>,值为无穷大,不相关,跳过;
(6) 找到<A,C>,值为无穷大,不相关,跳过;
(7) 找到<A,B>,值为无穷大,不相关,跳过;
(8) 找到<A,D>,visit D;
(9) 迭代arc[5][j],寻找D指向的顶点,找到<D,E>,值为无穷大,不相关,跳过;
(10) 找到<D,F>,visit F;
(11) 迭代arc[1][j],寻找F指向的顶点,找到<F,E>,值为无穷大,不相关,跳过;
(12) 找到<F,C>,值为无穷大,不相关,跳过;
(13) 找到<F,A>,值为无穷大,不相关,跳过;
(14) 找到<F,B>,值为无穷大,不相关,跳过;
(15) 找到<F,D>,值为无穷大,不相关,跳过;
(16) F处理完毕,没有相关的顶点,于是回退一步,到D,继续迭代arc[5][j],找到<D,C>,visit C;
(17) 迭代arc[2][j],寻找C指向的顶点,找到<C,E>,E已被访问,跳过;
(18) 找到<C,F>,值为无穷大,不相关,跳过;
(19) 找到<C,A>,值为无穷大,不相关,跳过;
(20) 找到<C,B>,visit B,此时所有顶点均访问完毕,结束;
代码实现如下所示:
/*** 对图进行深度优先遍历** @author Korbin* @date 2023-02-02 17:02:23**/
public List<T> deepFirstTraverse() {List<T> visitedVertex = new ArrayList<>();boolean[] visited = new boolean[vertexNum];for (int i = 0; i < vertexNum && visitedVertex.size() < vertexNum; i++) {deepFirstTraverse(visitedVertex, visited, i);}return visitedVertex;}/*** 对图进行深度迭代** @param visitedVertex 迭代结果* @param visited 已访问过的顶点* @param index 接着要迭代的结点* @author Korbin* @date 2023-02-02 17:26:43**/
public void deepFirstTraverse(List<T> visitedVertex, boolean[] visited, int index) {// 取出当前顶点if (!visited[index]) {// 当前顶点未被访问,才继续T ver = vertex[index];visitedVertex.add(ver);visited[index] = true;// 取出当前顶点可走的边for (int j = 0; j < arc[index].length && visitedVertex.size() < vertexNum; j++) {if (j != index) {switch (type) {case UNDIRECTED:case DIRECTED: {// 无向图或有向图,为1且顶点未被访问表示可以走try {int weight = (int) (arc[index][j]);if (weight == 1 && !visited[j]) {// 可以继续往下走deepFirstTraverse(visitedVertex, visited, j);}} catch (NumberFormatException e) {// do nothing}break;}case UNDIRECTED_NETWORK:case DIRECTED_NETWORK: {// 无向图或有向网// 不为infinity,且顶点未被访问if (!arc[index][j].equals(infinity) && !visited[j]) {// 可以继续往下走deepFirstTraverse(visitedVertex, visited, j);}break;}}}}}
}
4.1.2 邻接表的深度优先遍历
考虑如下有向图:
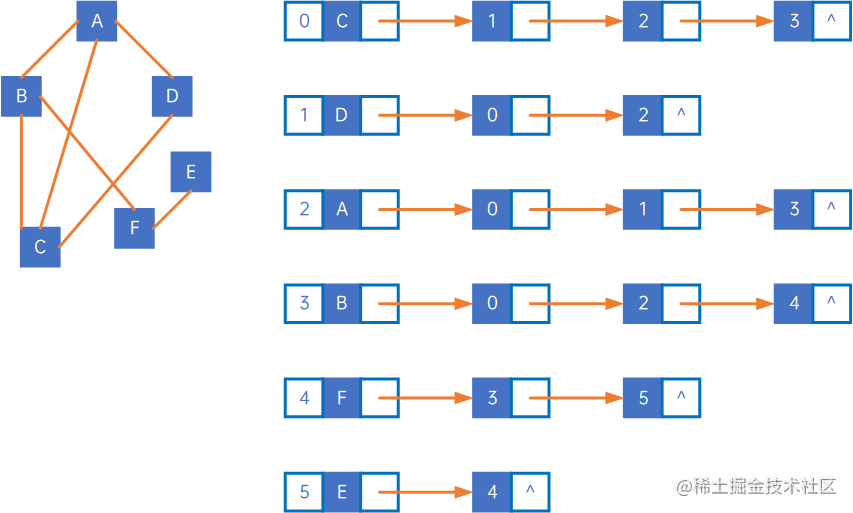
从第一个顶点开始,打到它未被访问的下一个顶点,寻找的过程是先找firstEdge,如果firstEdge指向的顶点已被访问,则找firstEdge的next,直到找到这个顶点为止;接着访问这个顶点的指向下一个未访问的顶点,寻找方式与第一个顶点相同。
该邻接表的遍历过程如下所示:
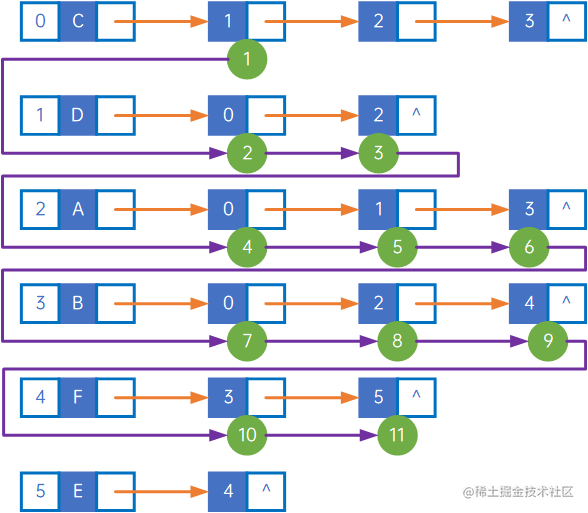
整体过程为:
(0) iterate C, visit C;
(1) 找顶点C相关的顶点,找到(C,D),visit D;
(2) 找顶点D相关的顶点,找到(D,C),两个顶点都被访问过,跳过;
(3) 继续找顶点D相关的顶点,找到(D,A),visit A;
(4) 找顶点A相关的顶点,找到(A,C),两个顶点都被访问过,跳过;
(5) 继续找顶点A相关的顶点,找到(A,D),两个顶点都被访问过,跳过;
(6) 继续找顶点A相关的顶点,找到(A,B),visit B;
(7) 找顶点B相关的顶点,找到(B,C),两个顶点都被访问过,跳过;
(8) 继续找顶点B相关的顶点,找到(B,A),两个顶点都被访问过,跳过;
(9) 继续找顶点B相关的顶点,找到(B,F),visit F;
(10) 找顶点F相关的顶点,找到(F,B),两个顶点都被访问过,跳过;
(11) 继续找顶点F相关的顶点,找到(F,E),visit E,此时所有顶点都访问完毕,结束;
相应地,有向图的邻接表遍历过程如下所示:
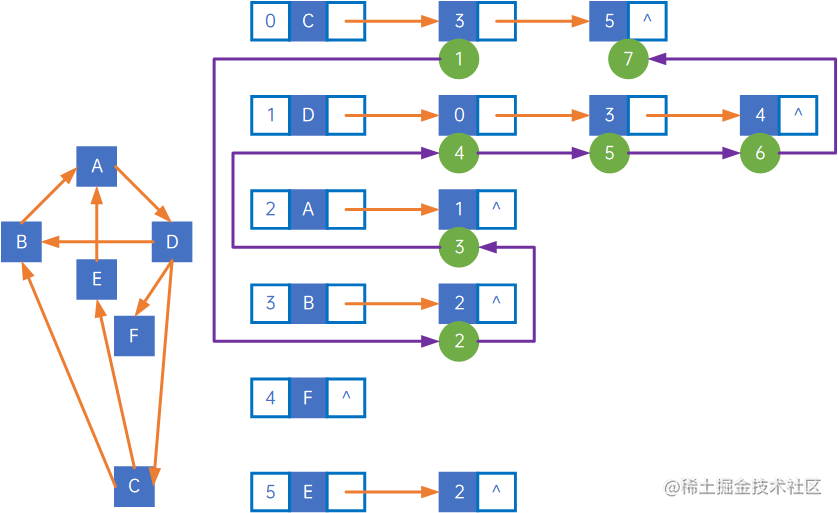
即:
(0) iterate C,visit C;
(1) 找顶点C指向的顶点,找到<C,B>,visit B;
(2) 找顶点B指向的顶点,找到<B,A>,visit A;
(3) 找顶点A指向的顶点,找到<A,D>,visit D;
(4) 找顶点D指向的顶点,找到<D,C>,两个顶点都被访问过,跳过;
(5) 继续找顶点D指向的顶点,找到<D,B>,两个顶点都被访问过,跳过;
(6) 继续找顶点D指向的顶点,找到<D,F>,visit F;F没有指向的顶点,回退到D;继续找顶点D指向的顶点,D所有指向的顶点都已访问,回退到B;继续找顶点B指向的顶点,B所有指向的顶点都已被访问,回退到C;
(7) 继续找顶点C指向的顶点,找到<C,E>,visit E,此时所有顶点访问完毕,结束;
除了邻接表外,还有一种逆邻接表,逆邻接表使用的遍历方法与邻接表不同,因为边集数组中保存的是每个顶点被指向的信息,如下:
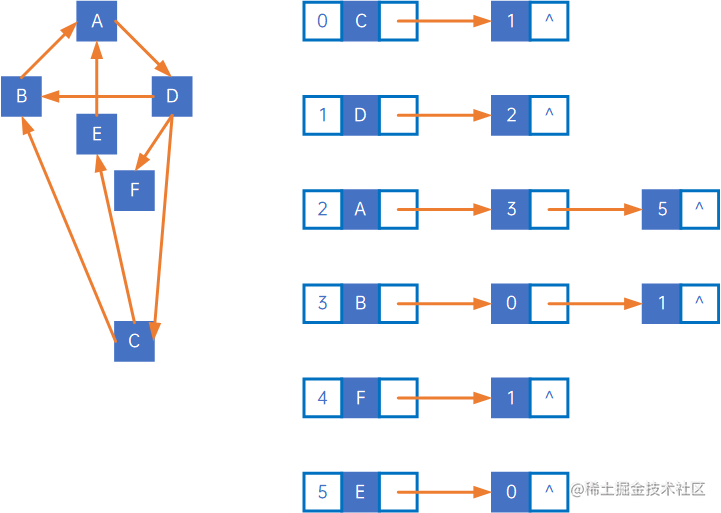
逆邻接表的查找下一个未访问顶点的过程,是“遍历边集数组,找到firstEdge或nextEdge的为当前顶点的边集数组结点,这个边集数组元素关联的第一个未被访问的顶点数组元素,就是要找的下一个顶点”,如上逆邻接表的遍历过程如下:
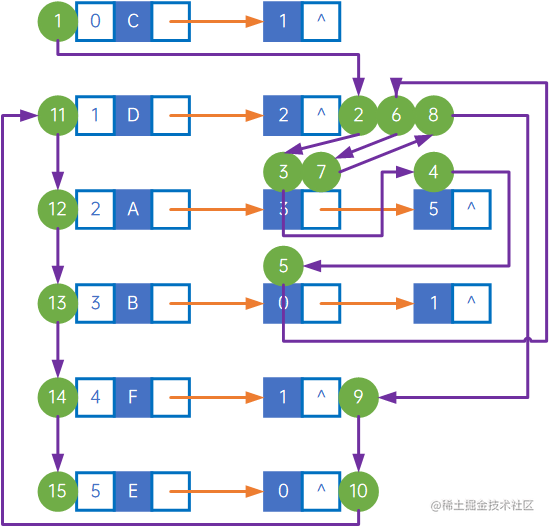
(1) 从第一个顶点C开始迭代,将它加入访问列表,visit C;
(2) 迭代所有边集数组,找到C指向的顶点,因为C已被访问,因此忽略它,先看D,只有边<A,D>,与顶点C不相关,跳过;
(3) 看顶点A,第一条边<B,A>,与顶点C不相关,跳过;
(4) 继续看顶点A,第二条边<E,A>,与顶点C不相关,跳过;
(5) A的边看完了,看B的边,第一条边<C,B>,找到顶点B是C指向的顶点,且由于是按下标从小到大迭代的,因此它一定是C指向的,且下标最小的顶点,因此,visit B;
(6) 接下来看顶点B指向的顶点,首先是顶点C,因为已访问过,因此忽略,然后是顶点D,有边<A,D>,与顶点B不相关,跳过;
(7) 然后看顶点A,有边<B,A>,A是顶点B指向的顶点,因此visit A;
(8) 接下来看顶点A指点的顶点,顶点C已被访问,仍然跳过,然后是顶点D,打到边<A,D>,符合要求,因此,visit D;
(9) 接下来看顶点D指向的顶点,前面的几个顶点C、D、A、B都已被访问过,跳过,看顶点F,有边<D,F>,符合要求,因此,visit F;
(10) 接下来看顶点F指向的顶点,前面的几个顶点C、D、A、B、F都已被访问,跳过,看顶点E,有边<C,E>,与顶点F不相关,跳过;
(11) 这时,所有顶点都迭代完毕,但仍未访问到所有顶点,因此回到第(1)步,继续迭代顶点,C已迭代过,于是看顶点D,顶点D已被访问,跳过;
(12) 继续,迭代顶点A,已被访问,跳过;
(13) 继续,迭代顶点B,已被访问,跳过;
(14) 继续,迭代顶点F,已被访问,跳过;
(15) 继续,迭代顶点E,未被访问,因此,visit E,此时,所有顶点都访问完毕,遍历结束;
代码实现如下所示:
/*** 对图进行深度优先遍历** @author Korbin* @date 2023-02-02 19:59:26**/
public List<T> deepFirstTraverse() {List<T> vertexList = new ArrayList<>();boolean[] visited = new boolean[vertexNum];// 对于邻接表,从第一个顶点开始处理,先处理firstEdgefor (int i = 0; i < vertexNum && vertexList.size() < vertexNum; i++) {if (!visited[i]) {System.out.println("iterate " + vertexes[i].getVertex());VertexNode<T, W> vertexNode = vertexes[i];vertexList.add(vertexNode.getVertex());visited[i] = true;if (reverseAdjacency) {deepFirstTraverse(vertexList, visited, i);} else {deepFirstTraverse(vertexList, visited, vertexNode);}}}return vertexList;
}/*** 对使用逆邻接表存储的图进行深度优先遍历** @param vertexList 遍历结果* @param visited 访问列表* @param index 当前遍历的下标* @author Korbin* @date 2023-02-06 18:13:34**/
public void deepFirstTraverse(List<T> vertexList, boolean[] visited, int index) {int minRefIndex = -1;// 找到index指向的下标最小的未访问的顶点boolean got = false;for (int i = 0; i < vertexNum && vertexList.size() < vertexNum && !got; i++) {if (!visited[i]) {VertexNode<T, W> vertexNode = vertexes[i];EdgeNode<W> edgeNode = vertexNode.getFirstEdge();while (null != edgeNode && vertexList.size() < vertexNum) {int edgeIndex = edgeNode.getIndex();System.out.format("check %s-%s\r\n", vertexes[edgeIndex].getVertex(), vertexes[i].getVertex());if (edgeIndex == index) {minRefIndex = i;got = true;break;}edgeNode = edgeNode.getNext();}}}if (minRefIndex != -1) {if (!visited[minRefIndex]) {// 访问这个顶点visited[minRefIndex] = true;vertexList.add(vertexes[minRefIndex].getVertex());System.out.println("in " + vertexes[minRefIndex].getVertex());// 再访问这个顶点指向的顶点deepFirstTraverse(vertexList, visited, minRefIndex);}}
}/*** 对使用邻接表存储的图进行深度优先遍历** @param vertexList 遍历结果* @param visited 已访问的顶点* @param vertexNode 正在访问的顶点* @author Korbin* @date 2023-02-03 20:26:22**/
public void deepFirstTraverse(List<T> vertexList, boolean[] visited, VertexNode<T, W> vertexNode) {EdgeNode<W> firstEdge = vertexNode.getFirstEdge();while (null != firstEdge && vertexList.size() < vertexNum) {System.out.format("check %s-%s\r\n", vertexNode.getVertex(), vertexes[firstEdge.getIndex()].getVertex());int index = firstEdge.getIndex();if (!visited[index]) {// 把它加入到遍历结果中,然后递归处理它对应的顶点VertexNode<T, W> nextNode = vertexes[index];vertexList.add(nextNode.getVertex());visited[index] = true;deepFirstTraverse(vertexList, visited, nextNode);}// 取下一个edgefirstEdge = firstEdge.getNext();}
}
4.1.3 十字链表的深度优先遍历
十字链表是在邻接表上的进一步优化,因此十字链表的深度优先遍历方式与邻接表类似,邻接表是处理firstEdge,十字链表处理的是firstOut和nextHead,因为firstOut就等于邻接表(非逆邻接表)的firstEdge,而nextHead相关于邻接表的EdgeNode中的next,大致逻辑为:
(1) 从第一个顶点开始处理,按如下规则:
1) 如果顶点X未被访问,则访问它;
2) 找到顶点X的指向的下一个未被访问的顶点,我们知道,首先是firstOut,然后是firstOut之后弧结点的nextHead;
3) 找到这个顶点后,访问它,然后递归1)、2)步;
(2) 继续迭代顶点列表中的其他顶点,若还有未访问的顶点,则按(1)的规则处理,直到所有顶点处理完毕;
以下面的十字链表为例:
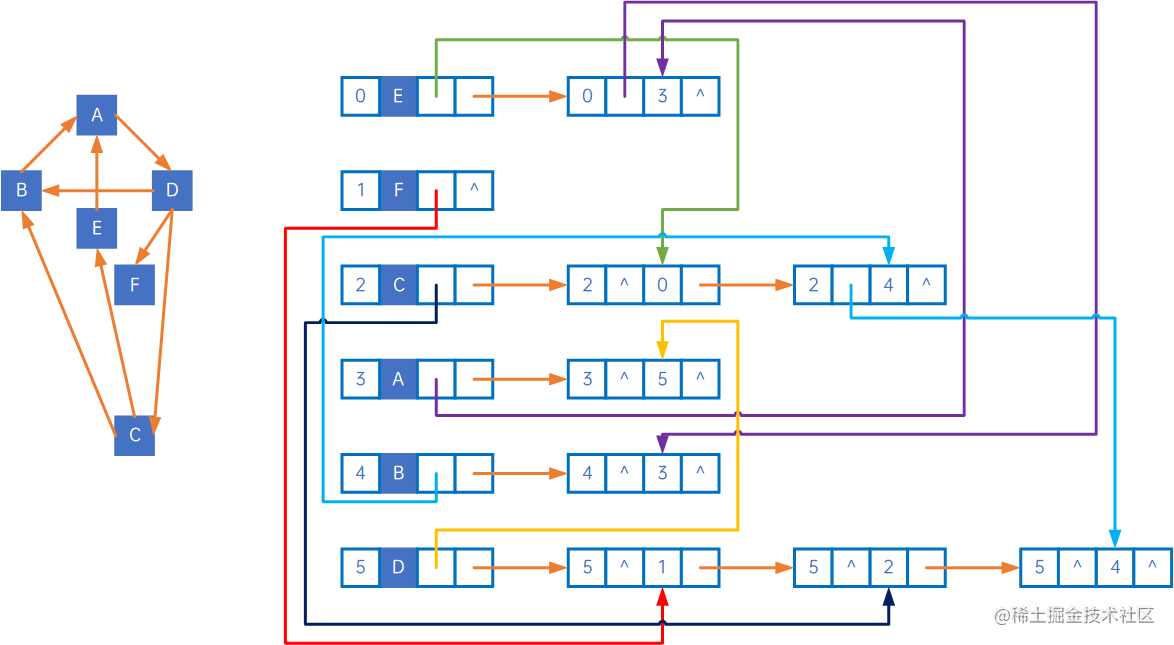
下图展示了它的深度优先遍历过程:
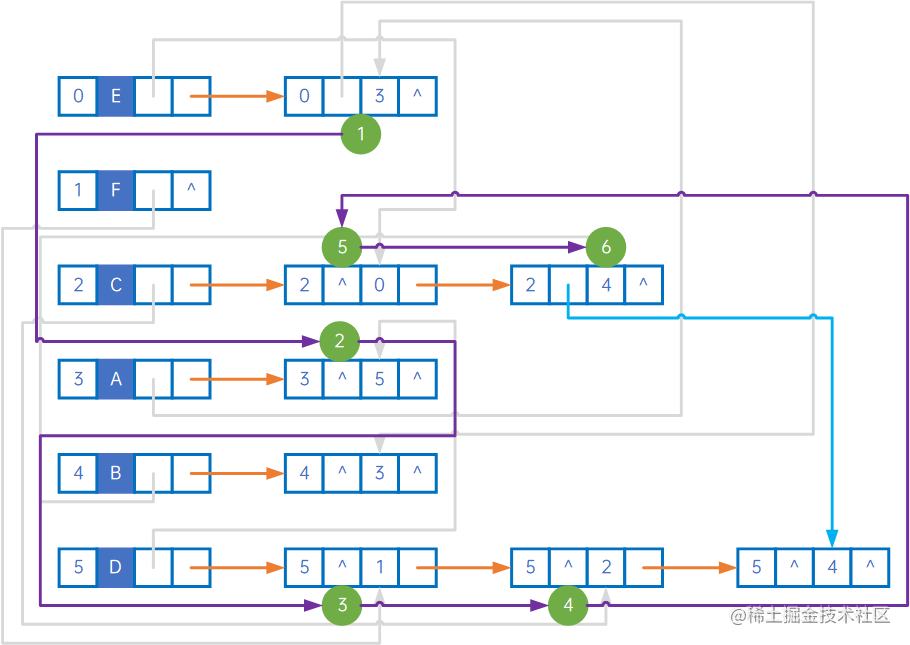
(0) 先忽略所有firstIn相关的线,然后iterate E,visit E;
(1) 找到E指向的顶点,找到<E,A>,visit A;
(2) 找到A指向的顶点,找到<A,D>,visit D;
(3) 找到D指向的顶点,找到<D,F>,visit F;F没有指向的顶点,因此回退到D;
(4) 找到D指向的顶点,找到<D,C>,visit C;
(5) 找到C指向的顶点,找到<C,E>,两个顶点都已被访问,跳过;
(6) 继续找到C指向的顶点<C,B>,visit B,此时所有顶点都已被访问,结束;
代码如下所示:
/*** 对图进行深度优先遍历** @author Korbin* @date 2023-02-02 19:59:26**/
public List<T> deepFirstTraverse() {List<T> vertexList = new ArrayList<>();boolean[] visited = new boolean[vertexNum];// 对于邻接表,从第一个顶点开始处理,先处理firstEdgefor (int i = 0; i < vertexNum && vertexList.size() < vertexNum; i++) {if (!visited[i]) {AcrossLinkVertexNode<T, W> vertexNode = vertexes[i];vertexList.add(vertexNode.getVertex());visited[i] = true;deepFirstTraverse(vertexList, visited, vertexNode);}}return vertexList;
}/*** 对图进行深度优先遍历** @param vertexList 遍历结果* @param visited 已访问于列表* @param vertexNode 待处理的顶点* @author Korbin* @date 2023-02-03 19:33:32**/
private void deepFirstTraverse(List<T> vertexList, boolean[] visited, AcrossLinkVertexNode<T, W> vertexNode) {AcrossLinkEdgeNode<W> firstEdge = vertexNode.getFirstOut();int nextIndex = -1;while (null != firstEdge && vertexList.size() < vertexNum) {// 指向的顶点下标为headIndexint index = firstEdge.getHeadIndex();if (!visited[index]) {vertexList.add(vertexes[index].getVertex());visited[index] = true;nextIndex = index;// 递归处理下一个顶点的邻边deepFirstTraverse(vertexList, visited, vertexes[nextIndex]);}firstEdge = firstEdge.getNextHead();}
}
4.1.4 邻接多重表的深度优先遍历
考虑如下邻接多重表:

第一个顶点是C,它有三条关联的边,分别是(C,A)、(C,B)和(C,D),我们把规则定为,下一个未访问的邻边是在顶点数组中下标最小,且未访问的那条边,这个定义与邻接多重表的存储结构相同,邻接多重表的存储设计是“firstEdge指向第一条边,iLink指向下一条边(下一条边的jVex必须为当前顶点),下一条边的jLink指向下下一条边(并不要求jVex为当前顶点),下下一条边的jLink指向下下一条边(并不要求jVex为当前顶点),依此类推”,因此邻接多重表深度优先遍历的过程是:
(1) 从第一个顶点X开始,找到这个顶点下一条未被访问的边(X,Y):
1) 若能找到Y,则访问Y,并查找Y的下一条未被访问的边;
2) 若Y不存在,则原路返回,走上一个顶点的未被访问的边;
(2) 递归执行第(1)步,直到找不到下一条未被访问的边时,继续对第二个顶点进行处理,直到所有顶点处理完毕。
如下为该邻接多重表的深度优先遍历过程:
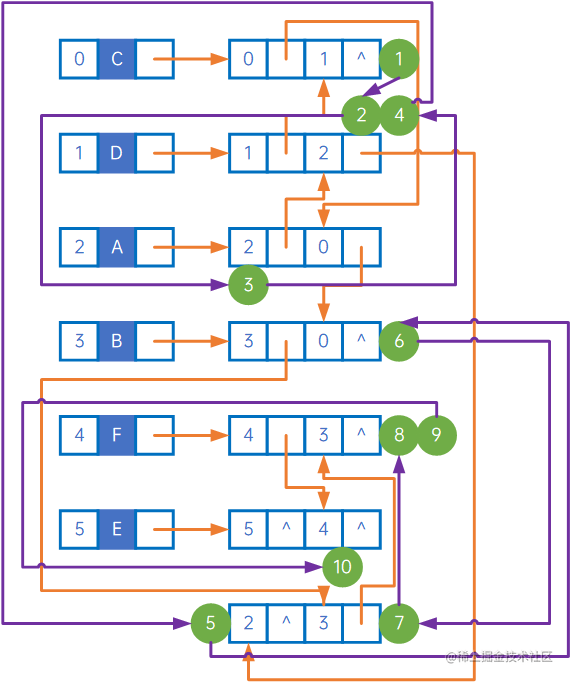
过程为:
(0) iterate C,visit C;
(1) 找C关联的顶点,找到(C,D),visit D;
(2) 找D关联的顶点,找到(D,A),visit A;
(3) 找A关联的顶点,找到(A,C),两个顶点都已访问,跳过;
(4) 继续找A关联的顶点,找到(D,A),两个顶点都已访问,跳过;
(5) 继续找A关联的顶点,找到(A,B),visit B;
(6) 找B关联的顶点,找到(B,C),两个顶点都已访问,跳过;
(7) 继续找B关联的顶点,找到(A,B),两个顶点都已访问,跳过;
(8) 继续找B关联的顶点,找到(F,B),visit F;
(9) 找F关联的顶点,找到(F,B),两个顶点都已访问,跳过;
(10) 继续找F关联的顶点,找到(E,F),visit E,所有顶点都已访问,结束;
实现代码如下所示:
/*** 对图进行深度优先遍历** @return 遍历结果* @author Korbin* @date 2023-02-03 17:09:46**/
public List<T> deepFirstTraverse() {List<T> vertexList = new ArrayList<>();boolean[] visited = new boolean[vertexNum];for (int i = 0; i < vertexNum && vertexList.size() < vertexNum; i++) {// 从第1个顶点开始找if (!visited[i]) {AdjacencyMultiVertexNode<T, W> vertexNode = vertexes[i];vertexList.add(vertexNode.getVertex());visited[i] = true;deepFirstTraverse(vertexList, visited, vertexNode);}}return vertexList;}/*** 对图进行深度优先遍历** @param vertexList 遍历结果* @param visited 顶点是否已被访问* @param vertexNode 待迭代的顶点* @author Korbin* @date 2023-02-03 17:44:43**/
public void deepFirstTraverse(List<T> vertexList, boolean[] visited, AdjacencyMultiVertexNode<T, W> vertexNode) {AdjacencyMultiEdgeNode<W> firstEdge = vertexNode.getFirstEdge();if (null != firstEdge) {// firstEdge的关联顶点下标是jVexint index = firstEdge.getJVex();int myIndex = firstEdge.getIVex();if (!visited[index]) {// 未访问AdjacencyMultiVertexNode<T, W> nextVertexNode = vertexes[index];vertexList.add(nextVertexNode.getVertex());visited[index] = true;// 然后处理index对应的顶点,找它的下一个未访问的邻边deepFirstTraverse(vertexList, visited, nextVertexNode);} else {// 已访问// 下一个相关边是firstEdge的iLinkAdjacencyMultiEdgeNode<W> nextEdge = firstEdge.getILink();if (null != nextEdge) {// 这个相关边的关联顶点是iVexindex = nextEdge.getIVex();if (!visited[index]) {// 未访问AdjacencyMultiVertexNode<T, W> nextVertexNode = vertexes[index];vertexList.add(nextVertexNode.getVertex());visited[index] = true;// 然后处理index对应的顶点,找它的下一个未访问的邻边deepFirstTraverse(vertexList, visited, nextVertexNode);} else {// 已访问// 下一条,以及下下条等,相关边都是jLinknextEdge = nextEdge.getJLink();while (null != nextEdge && vertexList.size() < vertexNum) {// 关联顶点可能是iVex,也可能是jVexint iVex = nextEdge.getIVex();int jVex = nextEdge.getJVex();if (iVex == myIndex) {// 关联顶点是JVexif (!visited[jVex]) {AdjacencyMultiVertexNode<T, W> nextVertexNode = vertexes[jVex];vertexList.add(nextVertexNode.getVertex());visited[jVex] = true;// 然后处理index对应的顶点,找它的下一个未访问的邻边deepFirstTraverse(vertexList, visited, nextVertexNode);} else {nextEdge = nextEdge.getJLink();}} else if (jVex == myIndex) {// 关联顶点是IVexif (!visited[iVex]) {AdjacencyMultiVertexNode<T, W> nextVertexNode = vertexes[iVex];vertexList.add(nextVertexNode.getVertex());visited[iVex] = true;// 然后处理index对应的顶点,找它的下一个未访问的邻边deepFirstTraverse(vertexList, visited, nextVertexNode);} else {nextEdge = nextEdge.getILink();}}}}}}}}
4.1.5 边集数组的深度优先遍历
边集数组存储了每条边的begin、end信息,由于无向图/网和有向图/网不同,无向图/网的begin和end可以是边上的任何一个顶点,因此对于无向图/网和有向图/网的遍历方式不同,但整体方向差不多:从下标最小的那个顶点开始,找每个顶点关联的、未被访问的、下标最小的那个顶点进行访问。
先看无向图/网:
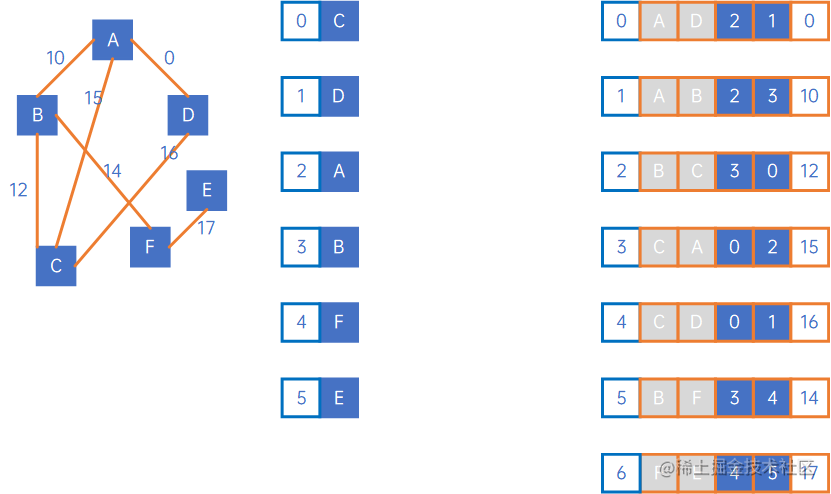
从下标最小的那个顶点开始找,即从顶点C开始找,找它的边,有(B,C)、(C,A)和(C,D),下标最小的关联顶点是D,然后找D的边,有(A,D)、(C,D),C被访问过了,因此下一个顶点是C,依此类推,整体过程如下:
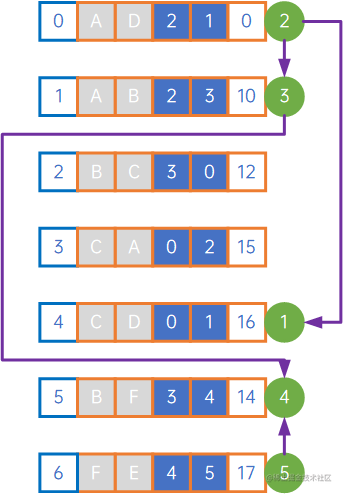
整体过程是:
(0) iterate C;
(1) 找到C关联的顶点,找到(C,D),visit C,visit D;
(2) 找到D关联的顶点,找到(A,D),visit A;
(3) 找到A关联的顶点,找到(A,B),visit B;
(4) 找到B关联的顶点,找到(B,F),visit F;
(5) 找到F关联的顶点,找到(F,E),visit E,所有顶点访问完毕,结束;
无向图/网在找“下一个顶点”时,找到的边中,可以begin等于当前顶点,也可以end等于当前顶点,但有向网则不同,只能找end为当前顶点的边,看如下有向图:
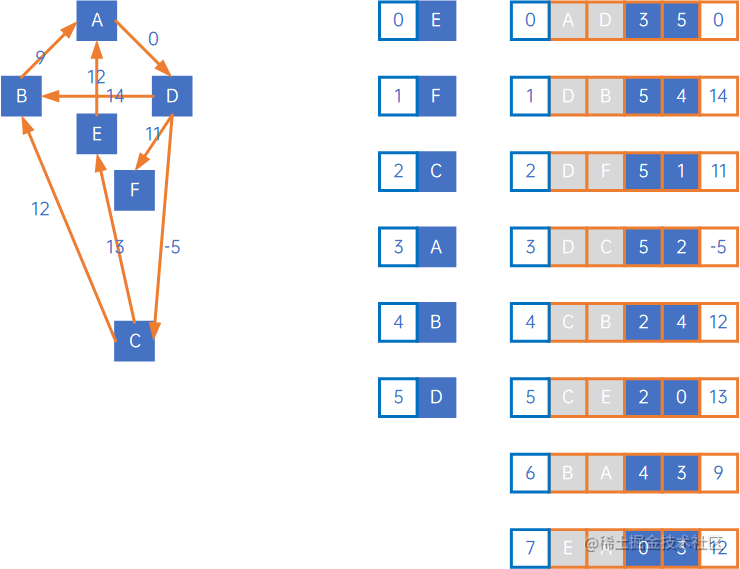
处理过程如下:
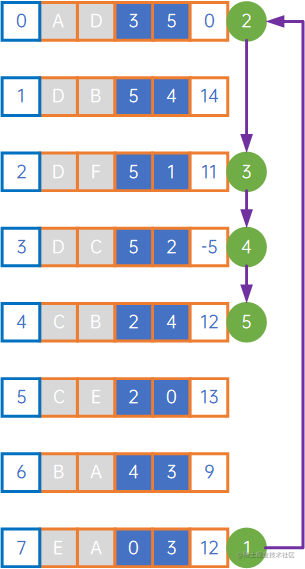
整体过程是:
(0) iterate E;
(1) 找E指向的顶点,找到<E,A>,visit E,visit A;
(2) 找A指向的顶点,找到<A,D>,visit D;
(3) 找D指向的顶点,找到<D,F>,visit F;F没有指向任何顶点,回退到D;
(4) 找D指向的顶点,找到<D,C>,visit C;
(5) 找C指向的顶点,找到<C,B>,visit B,此时,所有顶点访问完毕,结束;
代码实现如下所示:
/*** 对图进行深度优先遍历** @return 遍历结果* @author Korbin* @date 2023-02-06 14:25:42**/
public List<T> deepFirstTraverse() {List<T> vertexList = new ArrayList<>();boolean[] visited = new boolean[vertexNum];for (int i = 0; i < vertexNum && vertexList.size() < vertexNum; i++) {deepFirstTraverse(vertexList, visited, i);}return vertexList;
}/*** 对图进行深度优先遍历** @param vertexList 遍历结果* @param visited 访问记录* @param index 待处理的下标* @author Korbin* @date 2023-02-06 14:25:58**/
public void deepFirstTraverse(List<T> vertexList, boolean[] visited, int index) {// 找下标为i的顶点关联的边中,关联顶点下标最小且未访问的顶点int minReleVertex = -1;for (int j = 0; j < arc.length && vertexList.size() < vertexNum; j++) {EdgeListEdgeNode<W> edgeNode = arc[j];int begin = edgeNode.getBegin();int end = edgeNode.getEnd();switch (type) {case UNDIRECTED:case UNDIRECTED_NETWORK: {if (begin == index && !visited[end]) {if (minReleVertex == -1 || minReleVertex > end) {minReleVertex = end;}} else if (end == index && !visited[begin]) {if (minReleVertex == -1 || minReleVertex > begin) {minReleVertex = begin;}}break;}case DIRECTED:case DIRECTED_NETWORK: {if (begin == index && !visited[end]) {if (minReleVertex == -1 || minReleVertex > end) {minReleVertex = end;}}break;}}}if (!visited[index]) {// 访问该顶点visited[index] = true;vertexList.add(vertex[index]);}if (minReleVertex != -1 && !visited[minReleVertex]) {// 访问该顶点的下标最小的关联顶点visited[minReleVertex] = true;vertexList.add(vertex[minReleVertex]);// 接下来,访问关联顶点的“下标最小的关联顶点”deepFirstTraverse(vertexList, visited, minReleVertex);// 处理完毕后,应继续处理本顶点,即“下一个顶点没有关联的顶点,因此回退一步”deepFirstTraverse(vertexList, visited, index);}}
4.2 广度优先遍历
广度优先遍历(Breadth First Search),又称为广度优先搜索,简称BFS,广度优先遍历有点类似于树的层序遍历。
4.2.1 邻接矩阵的广度优先遍历
考虑如下无向图:
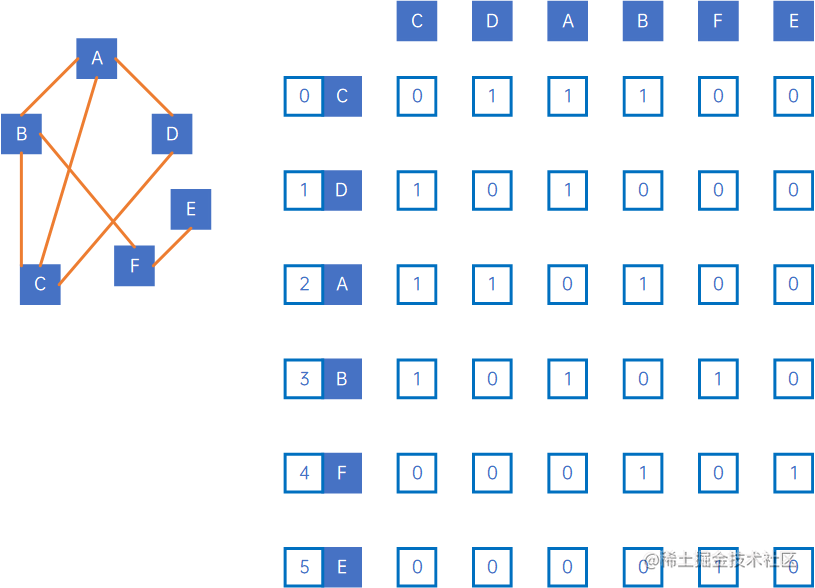
广度优先遍历的方法是:从下标最小的顶点C开始,访问C,然后找到它的下一层,访问它的下一层,然后找到下一层的下一层,访问它们,依此类推。
在无向图中我们这边实现:
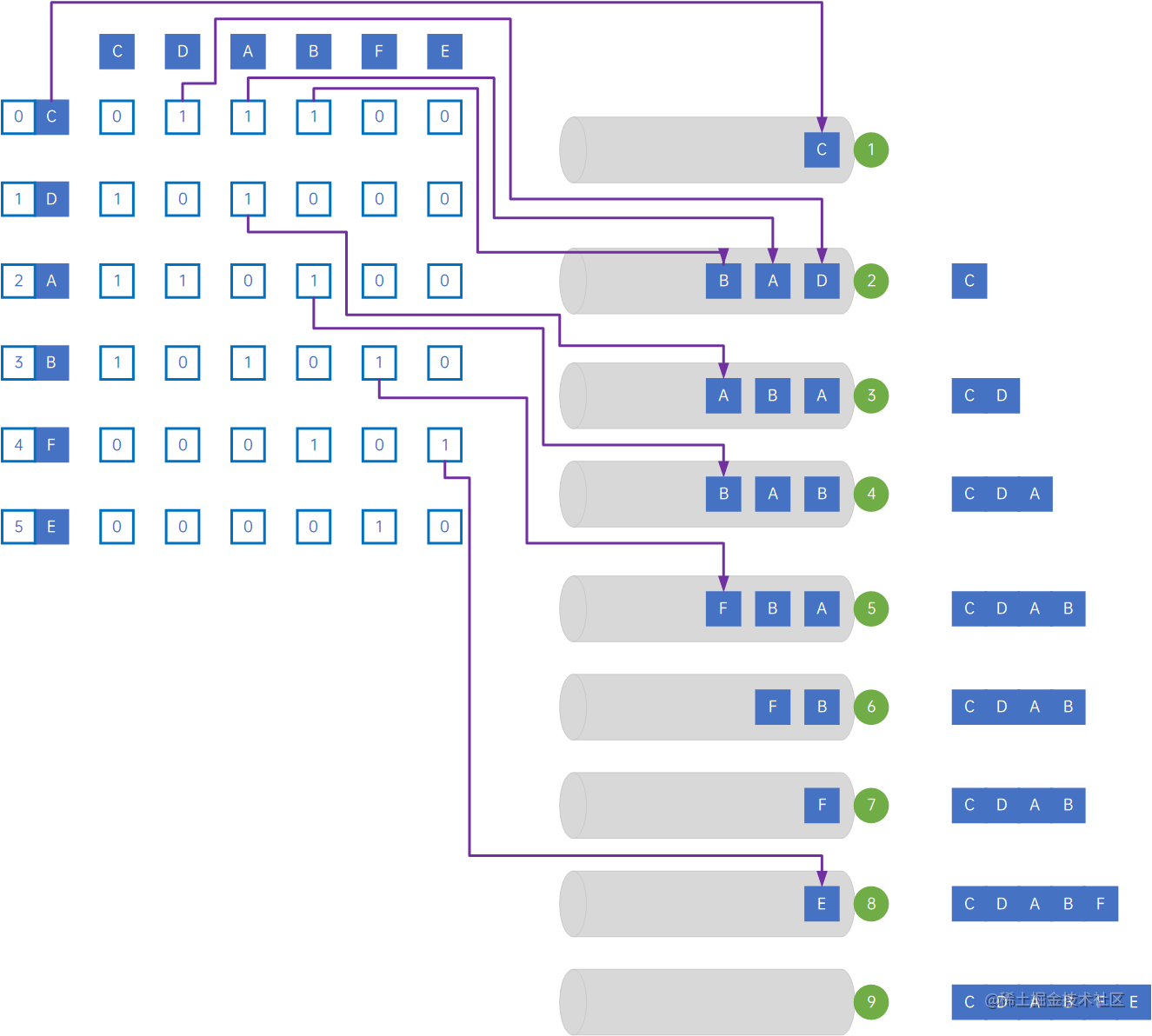
(0) 我们先建一个队列用于辅助;
(1) 从顶点C开始,把它的下标加入队列,此时队列里面只有C;
(2) 从队列中取出队头的数据,即C的下标0,访问C,然后迭代arc[0][j],weight为1的依次加入队列,此时队列从尾到头依次是B、A、D,已访问列表里有{C};
(3) 从队列中取出队头的数据,即D的下标1,访问D,然后迭代arc[1][j],weight为1且未被访问的依次加入队列,此时队列从尾到头依次是A、B、A,已访问列表里有{C, D};
(4) 从队列中取出队头的数据,即A的下标2,访问A,然后迭代arc[2][j],weight为1且未被访问的依次加入队列,此时队列从尾到头依次是B、A、B,已访问列表里有{C, D, A};
(5) 从队列中取出队头的数据,即B的下标3,访问B,然后迭代arc[3][j],weight为1且未被访问的依次加入队列,此时队列从尾到头依次是F、B、A,已访问列表里有{C, D, A, B};
(6) 从队列中取出队头的数据,即A的下标2,发现A已被访问,跳过,此时队列从尾到头依次是F、B,已访问列表里有{C, D, A, B};
(7) 从队列中取出队头的数据,即B的下标3,发现B已被访问,跳过,此时队列从尾到头依次是F,已访问列表里有{C, D, A, B};
(8) 从队列中取出队头的数据,即F的下标4,访问F,然后迭代arc[4][j],weight为1且未被访问的依次加入队列,此时队列从尾到头依次是E,已访问列表里有{C, D, A, B, F};
(9) 从队列中取出队头的数据,即E的下标5,访问E,这时发现所有顶点均已访问完毕,结束遍历,得到结果{C, D, A, B, F, E};
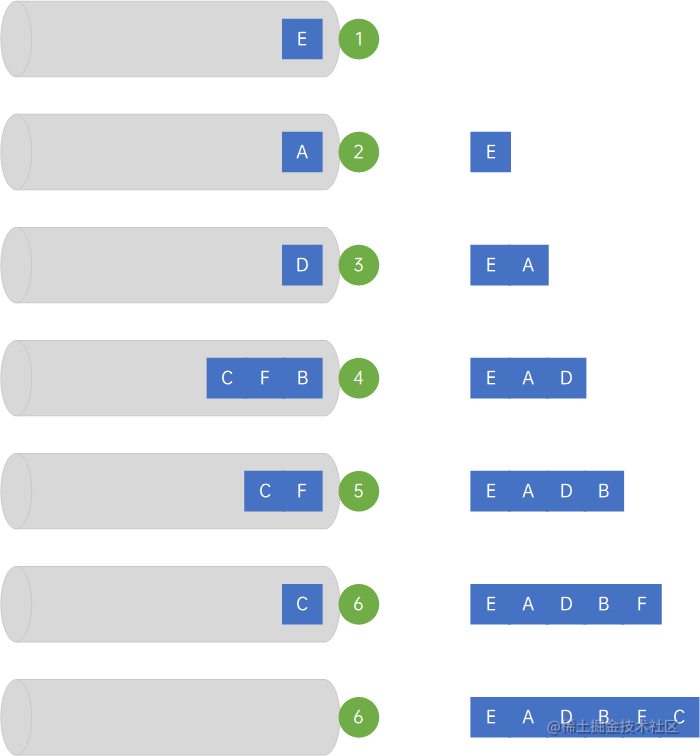
有向图/网的实现类似,考虑如下有向网:
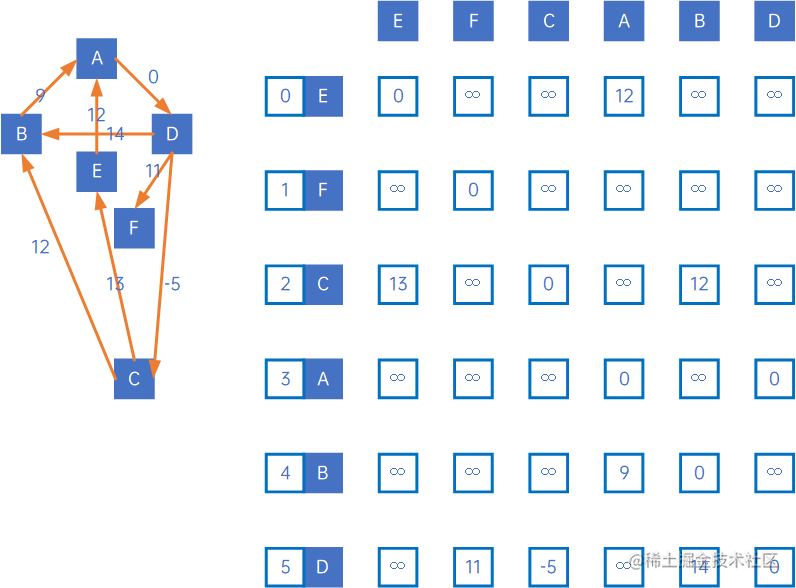
遍历过程如下所示:
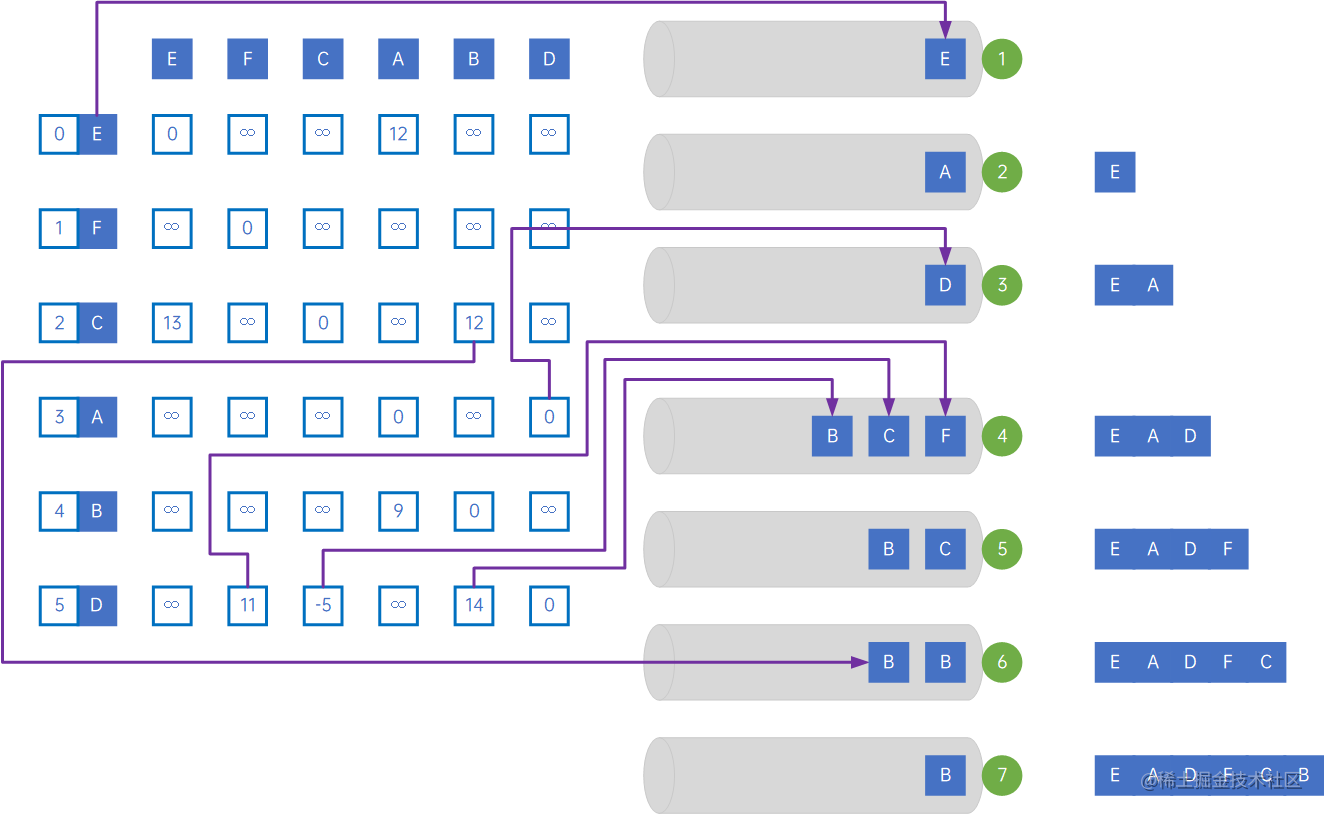
(1) 仍然使用一个辅助队列,用于存储顶点下标,从下标为0的顶点开始迭代,先将它入队,此时队列里面只有E;
(2) 从队列中取出队头数据,即E的下标0,访问它,迭代arc[0][j],取出相关边,有<E,A>,将A插入队列,此时队列里面只有A,已访问顶点列表为{E};
(3) 从队列中取出队头数据,即A的下标3,访问它,迭代arc[3][j],取出相关边,有<A,D>,将D插入队列,此时队列里面只有D,已访问顶点列表为{E, A};
(4) 从队列中取出队头数据,即D的下标5,访问它,迭代arc[5][j],取出相关边,有<D,F>、<D,C>、<D,B>,将F、C、B依次插入队列,此时队列从队尾到队头依次是B、C、F,已访问顶点列表为{E, A, D};
(5) 从队列中取出队头数据,即F的下标1,访问它,迭代arc[1][j],取出相关边,没有,不进行处理,此时队列从队尾到队头依次是B、C,已访问顶点列表为{E, A, D, F};
(6) 从队列中取出队头数据,即C的下标2,访问它,迭代arc[2][j],取出相关边,有<C,E>、<C,B>,因为顶点E已被访问,因此忽略它,把B加入到队列,此时队列从队尾到队头依次是B、B,已访问顶点列表为{E, A, D, F, C};
(7) 从队列中取出队头数据,即B的下标4,访问它,发现所有顶点已访问完毕,遍历结束,得到结果{E, A, D, F, C, B};
代码实现如下所示:
/*** 对图进行广度优先遍历** @return 遍历结果* @author Korbin* @date 2023-02-06 19:33:16**/
public List<T> breadthFirstTraverse() {List<T> vertexList = new ArrayList<>();boolean[] visited = new boolean[vertexNum];LinkQueue<Integer> queue = new LinkQueue<>();queue.init();for (int i = 0; i < vertexNum && vertexList.size() < vertexNum; i++) {if (!visited[i]) {// 入队列LinkListNode<Integer> node = new LinkListNode<>();node.setData(i);queue.insert(node);System.out.println("iterate " + vertex[i]);while (!queue.isEmpty() && vertexList.size() < vertexNum) {// 一个个取出来访问,并把它们的下一层放入队列node = queue.delete();int index = node.getData();if (!visited[index]) {vertexList.add(vertex[index]);visited[index] = true;System.out.println("in " + vertex[index]);for (int j = 0; j < vertexNum && vertexList.size() < vertexNum; j++) {if (j != index && !visited[j]) {boolean canInsert = false;switch (type) {case UNDIRECTED:case DIRECTED: {// 无向图和有向图,weight为1表示顶点相关try {int weight = (int) arc[index][j];if (weight == 1) {canInsert = true;}} catch (NumberFormatException e) {// do nothing}break;}case UNDIRECTED_NETWORK:case DIRECTED_NETWORK: {// 无向网和有向网,weight不为infinity表示顶点相关if (!arc[index][j].equals(infinity)) {canInsert = true;}}}if (canInsert) {// 把下一层入队node = new LinkListNode<>();node.setData(j);queue.insert(node);System.out.println("in queue " + vertex[j]);}}}}}}}return vertexList;
}
4.2.2 邻接表的广度优先遍历
与邻接矩阵相同,邻接表的广度优先遍历也借助队列实现,其中,逆邻接表的实现会更为复杂:
/*** 对图进行广度优先遍历** @return 遍历结果* @author Korbin* @date 2023-02-07 08:38:46**/
public List<T> breadthFirstTraverse() {List<T> vertexList = new ArrayList<>();boolean[] visited = new boolean[vertexNum];LinkQueue<Integer> queue = new LinkQueue<>();queue.init();for (int i = 0; i < vertexNum && vertexList.size() < vertexNum; i++) {System.out.println("iterate " + vertexes[i].getVertex());if (!visited[i]) {LinkListNode<Integer> node = new LinkListNode<>();node.setData(i);queue.insert(node);System.out.println("insert " + vertexes[i].getVertex());while (!queue.isEmpty() && vertexList.size() < vertexNum) {// 出队列node = queue.delete();System.out.println("get " + vertexes[node.getData()].getVertex());int index = node.getData();VertexNode<T, W> vertexNode = vertexes[index];// 访问该顶点if (!visited[index]) {vertexList.add(vertexNode.getVertex());visited[index] = true;System.out.println("visit " + vertexNode.getVertex());if (!reverseAdjacency) {// 邻接表// 把指向的顶点一一入队EdgeNode<W> edge = vertexNode.getFirstEdge();while (edge != null && vertexList.size() < vertexNum) {index = edge.getIndex();if (!visited[index]) {System.out.println("insert " + vertexes[index].getVertex());LinkListNode<Integer> childNode = new LinkListNode<>();childNode.setData(index);queue.insert(childNode);}edge = edge.getNext();}} else {// 逆邻表// 把指向的顶点一一入队for (int j = 0; j < vertexNum && vertexList.size() < vertexNum; j++) {if (j != index && !visited[j]) {VertexNode<T, W> tmpVertex = vertexes[j];EdgeNode<W> tmpEdge = tmpVertex.getFirstEdge();while (null != tmpEdge && vertexList.size() < vertexNum) {if (tmpEdge.getIndex() == index) {// 入队System.out.println(tmpEdge.getIndex() + "=======" + index + "=======" + j);System.out.println("insert " + vertexes[j].getVertex());LinkListNode<Integer> childNode = new LinkListNode<>();childNode.setData(j);queue.insert(childNode);break;}tmpEdge = tmpEdge.getNext();}}}}}}}}return vertexList;
}
4.2.3 十字链表的广度优先遍历
十字链表的实现与邻接表的实现相同:
/*** 对图进行广度优先遍历** @return 遍历结果* @author Korbin* @date 2023-02-07 09:56:29**/
public List<T> breadthFirstTraverse() {List<T> vertexList = new ArrayList<>();boolean[] visited = new boolean[vertexNum];LinkQueue<Integer> queue = new LinkQueue<>();queue.init();for (int i = 0; i < vertexNum && vertexList.size() < vertexNum; i++) {System.out.println("iterate " + vertexes[i].getVertex());if (!visited[i]) {LinkListNode<Integer> node = new LinkListNode<>();node.setData(i);queue.insert(node);System.out.println("insert " + vertexes[i].getVertex());while (!queue.isEmpty() && vertexList.size() < vertexNum) {// 出队列node = queue.delete();System.out.println("get " + vertexes[node.getData()].getVertex());int index = node.getData();AcrossLinkVertexNode<T, W> vertexNode = vertexes[index];// 访问该顶点if (!visited[index]) {vertexList.add(vertexNode.getVertex());visited[index] = true;System.out.println("visit " + vertexNode.getVertex());// 邻接表// 把指向的顶点一一入队AcrossLinkEdgeNode<W> edge = vertexNode.getFirstOut();while (edge != null && vertexList.size() < vertexNum) {index = edge.getHeadIndex();if (!visited[index]) {System.out.println("insert " + vertexes[index].getVertex());LinkListNode<Integer> childNode = new LinkListNode<>();childNode.setData(index);queue.insert(childNode);}edge = edge.getNextHead();}}}}}return vertexList;}
4.2.4 邻接多重表的广度优先遍历
上文有提到如何在邻接多重表中寻找关联的顶点,在进行广度遍历时,同样借助队列实现:
/*** 对图进行广度优先遍历** @return 遍历结果* @author Korbin* @date 2023-02-07 10:03:26**/
public List<T> breadthFirstTraverse() {List<T> vertexList = new ArrayList<>();boolean[] visited = new boolean[vertexNum];LinkQueue<Integer> queue = new LinkQueue<>();queue.init();for (int i = 0; i < vertexNum && vertexList.size() < vertexNum; i++) {if (!visited[i]) {System.out.println("iterate " + vertexes[i].getVertex());// 入队LinkListNode<Integer> node = new LinkListNode<>();node.setData(i);queue.insert(node);System.out.println("insert " + vertexes[i].getVertex());while (!queue.isEmpty() && vertexList.size() < vertexNum) {// 从队列中取出int index = queue.delete().getData();System.out.println("get " + vertexes[index].getVertex());if (!visited[index]) {// 访问它AdjacencyMultiVertexNode<T, W> vertexNode = vertexes[index];vertexList.add(vertexNode.getVertex());visited[index] = true;System.out.println("visit " + vertexNode.getVertex());// 取index关联的顶点AdjacencyMultiEdgeNode<W> firstEdge = vertexNode.getFirstEdge();if (null != firstEdge) {int childIndex = firstEdge.getJVex();if (!visited[childIndex]) {// 相关顶点入队LinkListNode<Integer> childNode = new LinkListNode<>();childNode.setData(childIndex);queue.insert(childNode);System.out.println("insert " + vertexes[childIndex].getVertex());}AdjacencyMultiEdgeNode<W> edgeNode = firstEdge.getILink();while (null != edgeNode && vertexList.size() < vertexNum) {// 可能是iVex等于当前顶点,也可能是jVex等于当前顶点int iVex = edgeNode.getIVex();int jVex = edgeNode.getJVex();if (iVex == index && !visited[jVex]) {// 相关顶点是jVexLinkListNode<Integer> childNode = new LinkListNode<>();childNode.setData(jVex);queue.insert(childNode);System.out.println("insert " + vertexes[jVex].getVertex());} else if (jVex == index && !visited[iVex]) {// 相关顶点是iVexLinkListNode<Integer> childNode = new LinkListNode<>();childNode.setData(iVex);queue.insert(childNode);System.out.println("insert " + vertexes[iVex].getVertex());}edgeNode = edgeNode.getJLink();}}}}}}return vertexList;
}
4.2.5 边集数组的广度优先遍历
边集数组仍然需要多次迭代边集数组,才能找到相关的顶点:
/*** 对图进行广度优先遍历** @return 遍历结果* @author Korbin* @date 2023-02-07 10:30:36**/
public List<T> breadthFirstTraverse() {List<T> vertexList = new ArrayList<>();boolean[] visited = new boolean[vertexNum];LinkQueue<Integer> queue = new LinkQueue<>();queue.init();boolean[] visitedArc = new boolean[edgeNum];for (int i = 0; i < vertexNum && vertexList.size() < vertexNum; i++) {if (!visited[i]) {System.out.println("iterate " + vertex[i]);// 入队LinkListNode<Integer> node = new LinkListNode<>();node.setData(i);queue.insert(node);System.out.println("insert " + vertex[i]);while (!queue.isEmpty() && vertexList.size() < vertexNum) {// 取出int index = queue.delete().getData();System.out.println("get " + vertex[index]);if (!visited[index]) {// 访问它vertexList.add(vertex[index]);visited[index] = true;System.out.println("visit " + vertex[index]);// 找它相关的顶点或指向的顶点switch (type) {case UNDIRECTED:case UNDIRECTED_NETWORK: {// 无向图/网for (int j = 0; j < edgeNum && vertexList.size() < vertexNum; j++) {if (!visitedArc[j]) {System.out.println("iterate arc " + j);EdgeListEdgeNode<W> edge = arc[j];int begin = edge.getBegin();int end = edge.getEnd();if (begin == index) {if (!visited[end]) {// 入队LinkListNode<Integer> childNode = new LinkListNode<>();childNode.setData(end);queue.insert(childNode);System.out.println("insert " + vertex[end]);}} else if (end == index) {if (!visited[begin]) {// 入队LinkListNode<Integer> childNode = new LinkListNode<>();childNode.setData(begin);queue.insert(childNode);System.out.println("insert " + vertex[begin]);}}if (visited[begin] && visited[end]) {visitedArc[j] = true;}}}break;}case DIRECTED:case DIRECTED_NETWORK: {for (int j = 0; j < edgeNum && vertexList.size() < vertexNum; j++) {if (!visitedArc[j]) {System.out.println("iterate arc " + j);EdgeListEdgeNode<W> edge = arc[j];int begin = edge.getBegin();int end = edge.getEnd();if (begin == index && !visited[end]) {// 入队LinkListNode<Integer> childNode = new LinkListNode<>();childNode.setData(end);queue.insert(childNode);System.out.println("insert " + vertex[end]);}if (visited[begin] && visited[end]) {visitedArc[j] = true;}}}break;}}}}}}return vertexList;
}
注意,边集数组若不进行特殊处理的话,每一层的顶点顺序取决于边集数组中结点顺序的定义。,如下有向网:
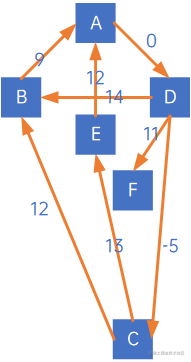
若定义为如下边集数组时:
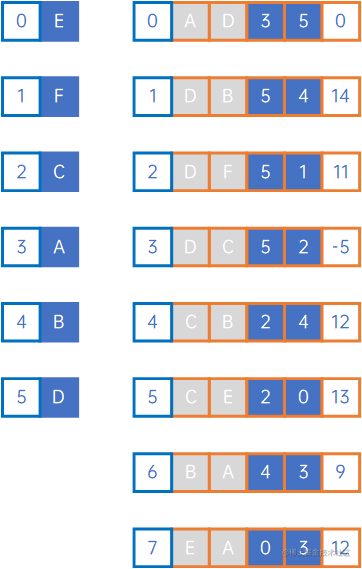
广度优先遍历过程为:
广度优先遍历结果为EADBFC。
但如果把边集数组的定义做一些调整:
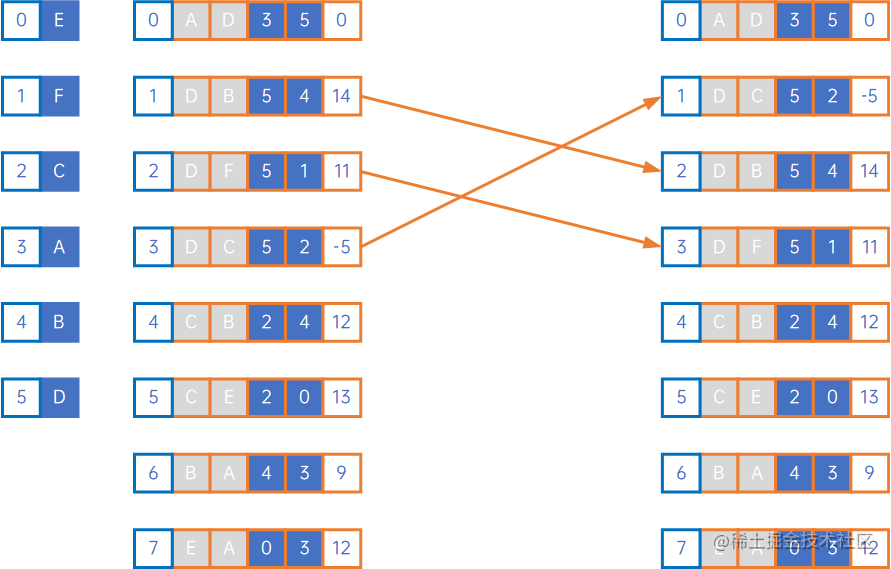
广度优先遍历过程为:
遍历结果为EADCBF,与之前的遍历结果并不相同。
当然,你也可以选择在取出所有相关的顶点后,对这些顶点按下标排序,那么广度优先遍历的结果就是固定的了,与边集数组中结点的顺序无关。
注:本文为程 杰老师《大话数据结构》的读书笔记,其中一些示例和代码是笔者阅读后自行编制的。
相关文章:

大话数据结构-图的深度优先遍历和广度优先遍历
4 图的遍历 图的遍历分为深度优先遍历和广度优先遍历两种。 4.1 深度优先遍历 深度优先遍历(Depth First Search),也称为深度优先搜索,简称DFS,深度优先遍历,是指从某一个顶点开始,按照一定的规…...

c语言指针怎么理解 第一部分
不理解指针,是因为有人教错了你。 有人告诉你,指针是“指向”某某某的,那就是误导你,给你挖了个坑。初学者小心不要误读这“指向”二字。 第一,“指针”通常用于保存一个地址,这个地址的数据类型在定义指…...
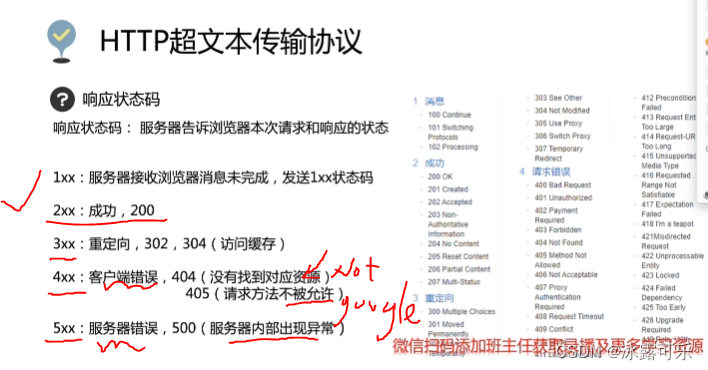
计算机网络安全基础知识2:http超文本传输协议,请求request消息的get和post,响应response消息的格式,响应状态码
计算机网络安全基础知识: 2022找工作是学历、能力和运气的超强结合体,遇到寒冬,大厂不招人,可能很多算法学生都得去找开发,测开 测开的话,你就得学数据库,sql,oracle,尤…...

Pytest自动化框架~权威教程03-原有TestSuite的执行方法
前言TestSuite一直是unittest的灵活与精髓之处, 在繁多的测试用例中, 可以任意挑选和组合各种用例集, 比如smoke用例集, level1用例集, webtest用例集, bug回归用例集等等, 当然这些TestSuite需要我们提前定义好, 并把用例加载进去.Pytest采取的是完全不同的用例组织和运行方式…...

web自动化 基于python+Selenium+PHP+Ftp实现的轻量级web自动化测试框架
1、 开发环境 win7 64 PyCharm 4.0.5 setuptools-29.0.1.zip 下载地址:setuptools-29.0.1.zip_免费高速下载|百度网盘-分享无限制 官方下载地址:setuptools PyPI python 3.3.2 mysql-connector-python-2.1.4-py3.3-win64 下载地址:mysq…...

【MyBatis】源码学习 05 - 关于 xml 文件解析的分析
文章目录前言参考目录学习笔记1、章节目录概览2、14.3:SqlSourceBuilder 类与 StaticSqlSource 类3、14.4.2:ResultMapResolver 类3.1、测试代码说明3.2、结果集 userMap 解析流程3.3、结果集 getGirl 解析流程3.4、鉴别器 discriminator 解析流程4、14.…...
代码随想录算法训练营第二天| 977. 有序数组的平方、209. 长度最小子数组、59.螺旋矩阵II
977 有序数组的平方题目链接:977 有序数组的平方介绍给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。思路看到题目的第一反应,首先负数的平方跟正数的平方是相同的&…...
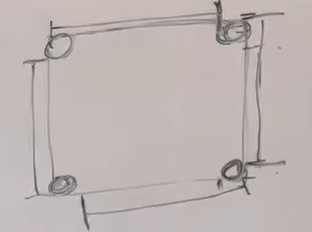
Ethercat系列(10)用QT实现SOEM主站
首先将SOEM编译成静态Lib库可以参考前面的博文(83条消息) VS2017下编译SOEM(Simle Open EtherCAT Master)_soem vs_CoderIsArt的博客-CSDN博客make_libsoem_lib.bat "C:\Program Files (x86)\Microsoft Visual Studio\2017\Community\VC\Auxiliary\Build" x86用QT创建…...

论文投稿指南——中文核心期刊推荐(科学、科学研究)
【前言】 🚀 想发论文怎么办?手把手教你论文如何投稿!那么,首先要搞懂投稿目标——论文期刊 🎄 在期刊论文的分布中,存在一种普遍现象:即对于某一特定的学科或专业来说,少数期刊所含…...
、attr()和data())
jQuery属性操作prop()、attr()和data()
jQuery 提供了一些属性操作的方法,主要包括 prop()、attr() 和 data() 等。通过这些方法,能够实现不同的需求。下面我们分别进行详细讲解。 1.prop() 方法 prop0 方法用来设置或获取元素固有属性值。元素固有属性是指元素本身自带的属性,如 …...
git的使用
1.git的四个区域: 2.常规git命令 git status 查看working directory哪些文件被更改了git add .把更改add到staging area,缓存的地方。改一个地方可以就先暂存一下,最后确认是哪些改动后再一起commit,以免不必要的版本。 在暂存区域ÿ…...
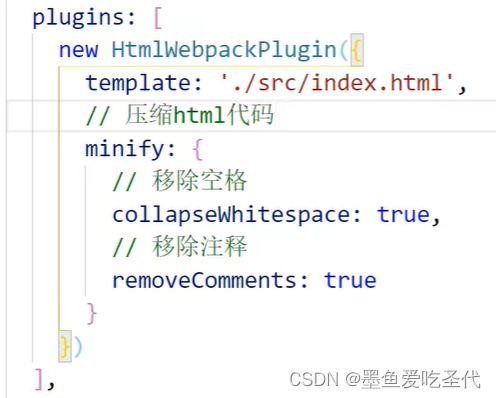
webpack生产环境配置
3 webpack生产环境配置 由于笔记文档没有按照之前的md格式书写,所以排版上代码上存在问题😢😢😢😢 09 提取css成单独文件 使用下载插件 npm i mini-css-extract-plugin0.9.0 -D webpack配置此时a,b提取成单独文件,并且…...
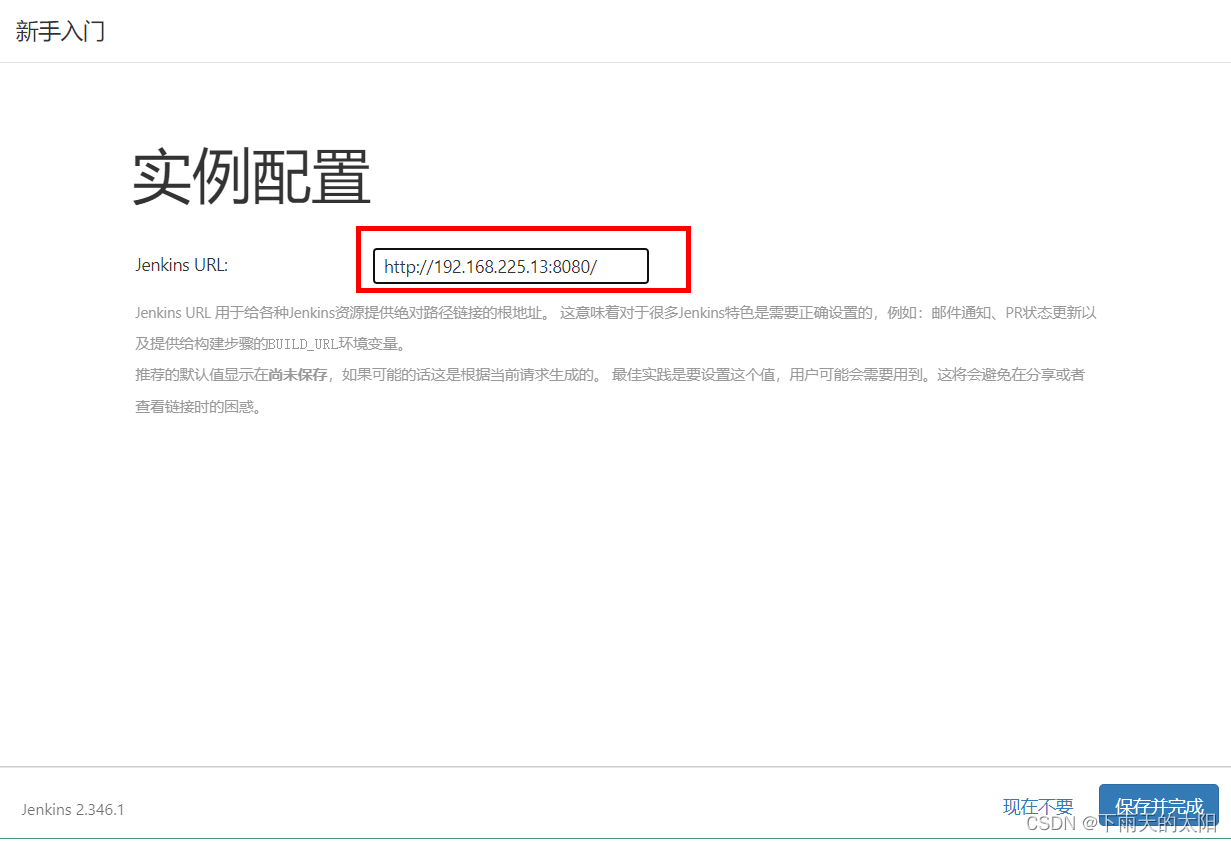
linux下安装jenkins
1.初始化Jenkins安装环境 系统版本:Red Hat Enterprise Linux 8.7 将脚本文件jenkins_install_env.sh 、 jenkins_install.sh和apache-maven-3.6.2-bin.tar.gz、jdk-8u251-linux-x64.tar.gz都上传到/usr/local/src目录下执行jenkins_install_env.sh脚本初始化Jenki…...

IGKBoard(imx6ull)-I2C接口编程之SHT20温湿度采样
文章目录1- 使能开发板I2C通信接口2- SHT20硬件连接3- 编码实现SHT20温湿度采样思路(1)查看sht20从设备地址(i2cdetect)(2)获取数据大体流程【1】软复位【2】触发测量与通讯时序(3)返…...
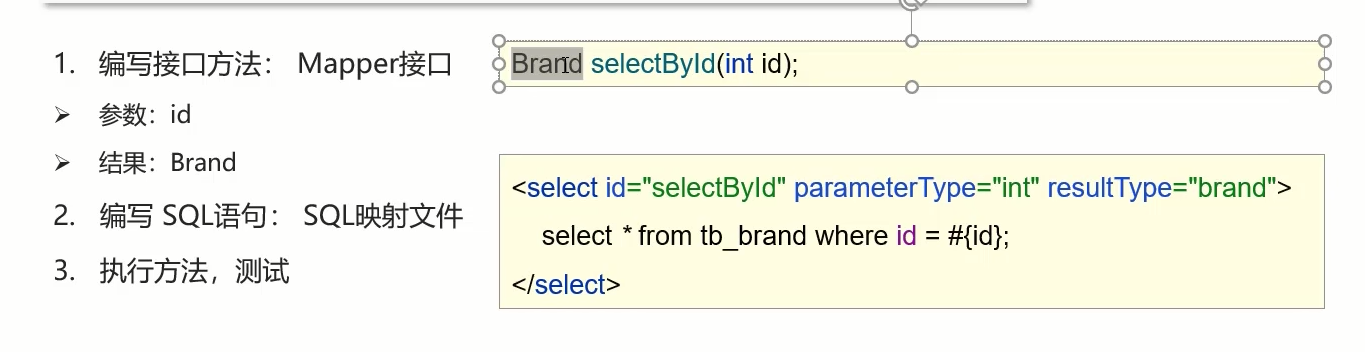
MyBatis——配置文件完成增删改查
1.首先先创建一个新的表,使用下面的sql语句 -- 删除tb_brand表 drop table if exists tb_brand; -- 创建tb_brand表 create table tb_brand (-- id 主键id int primary key auto_increment,-- 品牌名称brand_name varchar(20),-- 企业名称company_name varchar(20…...

Python内置函数 — all,any
1、all 源码注释: def all(*args, **kwargs): # real signature unknown"""Return True if bool(x) is True for all values x in the iterable.If the iterable is empty, return True."""pass 语法格式: all(iterable)…...
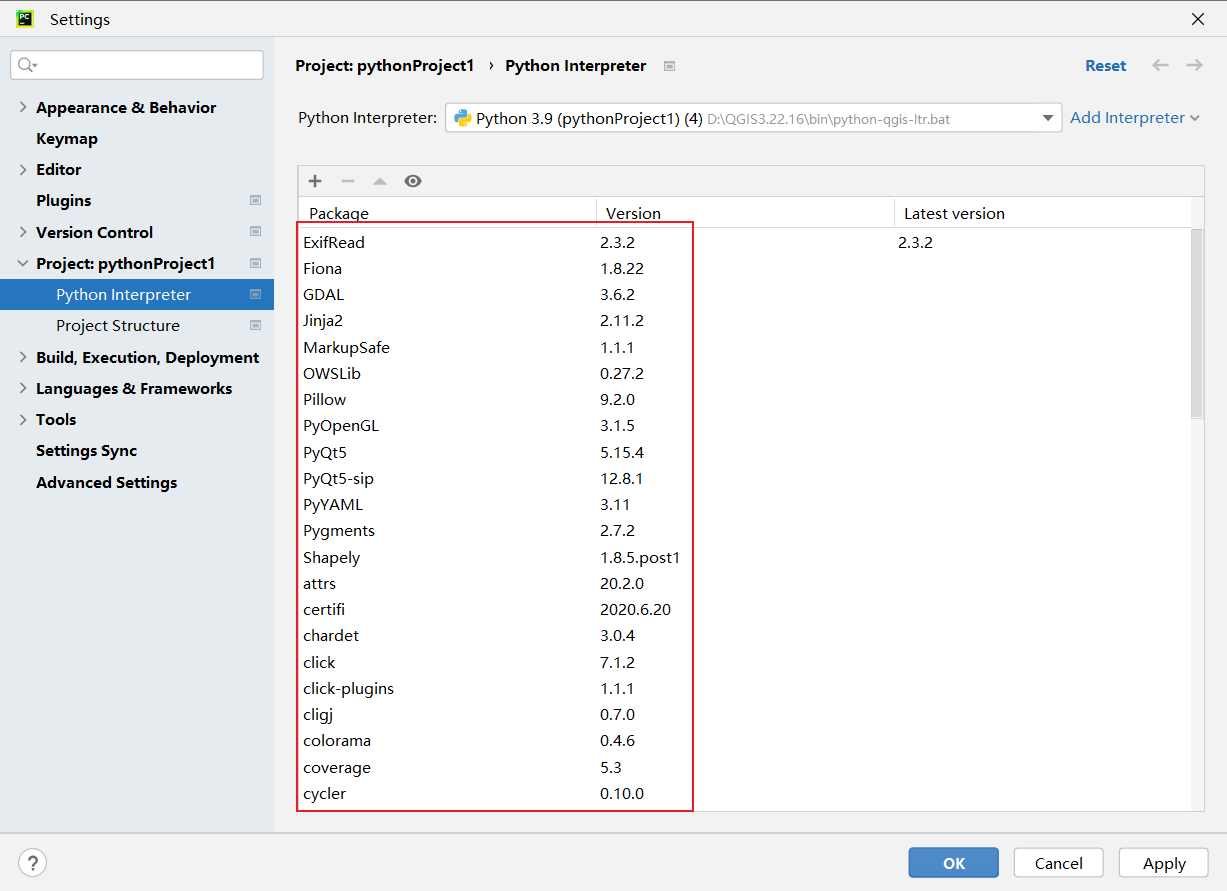
Pycharm配置QGIS环境
版本信息:QGIS: 3.22.16Pycharm:2022.3.2 (Community Edition)在QGIS官网下载安装包,下载稳定版本即可。配置步骤:安装完成后,使用Pycharm新建工程Python编译器选择之前配置好的编译器环境选择左侧第一个Vi…...
【C++】stack 与 queue
stack 与 queuestackSTL 容器中 stack 的使用模拟实现 stackqueueSTL 容器中 queue 的使用模拟实现 queuestack 在数据结构中,我们了解到,stack 栈结构,是一种先进后出的结构,并且我们是使用顺序表来进行实现栈的操作的。 STL 容…...

ARC142E Pairing Wizards
ARC142E Pairing Wizards 题目大意 有nnn个法师,编号为111到nnn。法师iii有强度aia_iai,他计划打败强壮度为bib_ibi的怪物。 你可以执行以下操作任意次: 选中一个法师,将它的强壮度增加1 一对法师(i,j)(i,j)(i,j)称为好的…...

Spark开发实战-主播打赏排行榜统计
(一)需求分析 计算每个大区当天金币收入排名前N的主播 背景: 我们有一款直播APP,已经在很多国家上线并运营了一段时间,产品经理希望开发一个功能,计算前N主播排行榜,按天更新排名信息…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...

算法打卡第18天
从中序与后序遍历序列构造二叉树 (力扣106题) 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 示例 1: 输入:inorder [9,3,15,20,7…...
