力扣单调栈算法专题训练
目录
- 1 专题说明
- 2 训练
1 专题说明
本博客用来计算力扣上的单调栈题目、解题思路和代码。
单调栈题目记录:
- 2232866美丽塔II


2 训练
题目1:2866美丽塔II。
解题思路:先计算出prefix[i],表示0~i满足递增情况下,0~i上的元素之和最大值。然后计算出suffix[i],表示i~n-1满足递增情况下,i~n-1上的元素之和最大值。那么以i为峰顶的美丽塔的元素之和的最大值为prefix[i] + suffix[i] - nums[i],遍历i,获得答案即可。
本质上,还是可以归类为:找到i左边,并且<=nums[i]的元素值。
C++代码如下,
class Solution {
public:long long maximumSumOfHeights(vector<int>& maxHeights) {int n = maxHeights.size();vector<long long> prefix(n, 0); //prefix[i]表示0~i是递增的情况下,0~i的元素之和stack<int> stk;for (int i = 0; i < n; ++i) {while (!stk.empty() && maxHeights[stk.top()] > maxHeights[i]) {stk.pop();}if (stk.empty()) {prefix[i] = (long long)(i + 1) * maxHeights[i];} else {prefix[i] = prefix[stk.top()] + (long long)(i - stk.top()) * maxHeights[i];}stk.push(i);}while (!stk.empty()) {stk.pop();}vector<long long> suffix(n, 0); //suffix[i]表示i~n-1是递减的情况下,i~n-1的元素之和for (int i = n - 1; i >= 0; --i) {while (!stk.empty() && maxHeights[stk.top()] > maxHeights[i]) {stk.pop();}if (stk.empty()) {suffix[i] = (long long)(n - i) * maxHeights[i];} else {suffix[i] = suffix[stk.top()] + (long long)(stk.top() - i) * maxHeights[i];}stk.push(i);}long long res = 0;for (int i = 0; i < n; ++i) {res = max(res, prefix[i] + suffix[i] - maxHeights[i]);}return res;}
};
python3代码如下,
class Solution:def maximumSumOfHeights(self, maxHeights: List[int]) -> int:n = len(maxHeights)prefix = [0 for i in range(n)] #0~i的递增数组的和的最大值stk = []for i in range(n):while len(stk) and maxHeights[stk[-1]] > maxHeights[i]:del stk[-1]if len(stk) == 0:prefix[i] = (i + 1) * maxHeights[i]else:prefix[i] = prefix[stk[-1]] + (i - stk[-1]) * maxHeights[i]stk.append(i)stk.clear()suffix = [0 for i in range(n)] #i~n-1的递减数组的和的最大值for i in range(n-1,-1,-1):while len(stk) and maxHeights[stk[-1]] > maxHeights[i]:del stk[-1]if len(stk) == 0:suffix[i] = (n - i) * maxHeights[i]else:suffix[i] = suffix[stk[-1]] + (stk[-1] - i) * maxHeights[i]stk.append(i)res = 0for i in range(n):#print(f"i = {i}, prefix[i] = {prefix[i]}, suffix[i] = {suffix[i]}.")res = max(res, prefix[i] + suffix[i] - maxHeights[i])return res
题目2:496下一个更大元素I。
解题思路:直接找右边首次大于它的元素即可。
C++代码如下,
class Solution {
public:vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2) {unordered_map<int,int> mp; //mp[x]表示nums2中元素x的右边,第一个比它大的元素stack<int> stk;for (int i = nums2.size() - 1; i >= 0; --i) {while (!stk.empty() && stk.top() <= nums2[i]) {stk.pop();}if (!stk.empty()) {mp[nums2[i]] = stk.top();} else {mp[nums2[i]] = -1;}stk.push(nums2[i]);}vector<int> res;for (auto x : nums1) {res.emplace_back(mp[x]);}return res;}
};
python3代码如下,
class Solution:def nextGreaterElement(self, nums1: List[int], nums2: List[int]) -> List[int]:n = len(nums2)mp = collections.defaultdict(int)stk = []for i in range(n - 1, -1, -1):while len(stk) and stk[-1] <= nums2[i]:del stk[-1]if len(stk):mp[nums2[i]] = stk[-1]else:mp[nums2[i]] = -1stk.append(nums2[i])res = []for x in nums1:res.append(mp[x])return res
题目3:503下一个更大元素II。
解题思路:环形问题,扩展两倍原数组即可,接下来就是找右侧首次大于它的元素。
C++代码如下,
class Solution {
public:vector<int> nextGreaterElements(vector<int>& nums) {int n = nums.size();vector<int> a(2 * n, 0);for (int i = 0; i < n; ++i) {a[i] = a[i + n] = nums[i];}vector<int> ans(2 * n, -1);stack<int> stk;for (int i = 2 * n - 1; i >= 0; --i) {while (!stk.empty() && stk.top() <= a[i]) {stk.pop();}if (!stk.empty()) {ans[i] = stk.top();}stk.push(a[i]);}vector<int> res(n, -1);for (int i = 0; i < n; ++i) {res[i] = ans[i];}return res;}
};
python3代码如下,
class Solution:def nextGreaterElements(self, nums: List[int]) -> List[int]:n = len(nums)a = [-1 for i in range(2 * n)]for i in range(n):a[i] = a[i + n] = nums[i]ans = [-1 for i in range(2 * n)]stk = []for i in range(2 * n - 1, -1, -1):while len(stk) and stk[-1] <= a[i]:del stk[-1]if len(stk):ans[i] = stk[-1]stk.append(a[i])res = [-1 for i in range(n)]for i in range(n):res[i] = ans[i]return res
题目4:2454下一个更大元素IV。
解题思路:比较难,不懂先放一边。
题目5:
相关文章:

力扣单调栈算法专题训练
目录 1 专题说明2 训练 1 专题说明 本博客用来计算力扣上的单调栈题目、解题思路和代码。 单调栈题目记录: 2232866美丽塔II 2 训练 题目1:2866美丽塔II。 解题思路:先计算出prefix[i],表示0~i满足递增情况下,0~i…...

【NI-RIO入门】理解Windows、Real Time与FPGA之间数据通信的原理
于NI kb摘录 1.概述 对于NI RIO系列设备(CompactRIO、sbRIO、myRIO等)进行编程时,需要注意有三个不同的组件。 人机界面 (HMI) 。有时称为“主机”,为用户提供图形用户界面(GUI),用于监控系统…...

关于游戏性能优化的技巧
关于游戏性能优化的技巧 游戏性能优化对象池Jobs、Burst、多线程间隔处理定时更新全局广播缓存组件缓存常用数据2D残影优化2D骨骼转GPU动画定时器优化DrawCall合批处理优化碰撞层优化粒子特效 游戏性能优化 好久没有在CSDN上面写文章了,今天突然看到鬼谷工作室技术…...
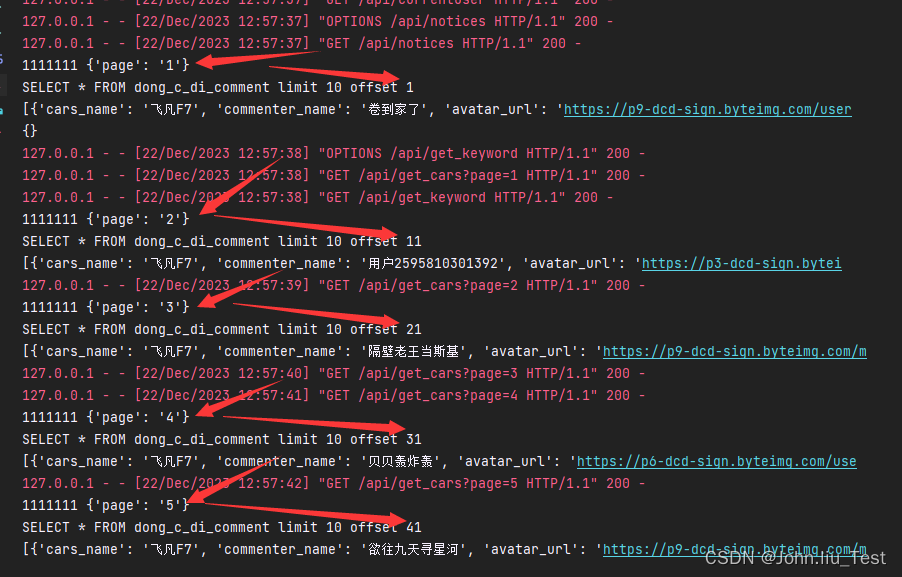
antdesignpro实现滚动加载分页数据
原理解析:每滚动一次相当于翻页,请求后端时给的页码参数要想办法加1,后端才能根据页码给出相应数据 注意后端收到页码参数之后要准确计算出每页的首行数据,关键逻辑代码: # 根据前端传的页码,进行计算下一…...
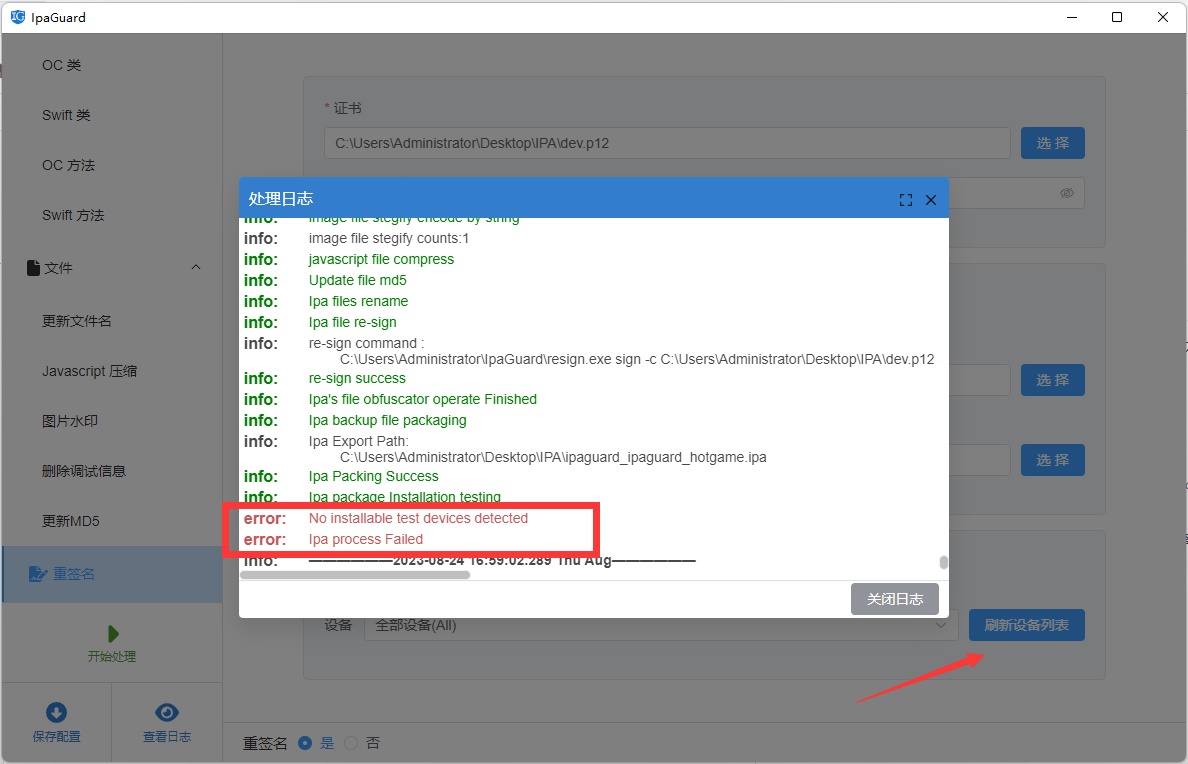
步兵 cocos2dx 加密和混淆
文章目录 摘要引言正文代码加密具体步骤代码加密具体步骤测试和配置阶段IPA 重签名操作步骤 总结参考资料 摘要 本篇博客介绍了针对 iOS 应用中的 Lua 代码进行加密和混淆的相关技术。通过对 Lua 代码进行加密处理,可以确保应用代码的安全性,同时提高性…...

【算法设计与分析】——动态规划算法
🎃个人专栏: 🐬 算法设计与分析:算法设计与分析_IT闫的博客-CSDN博客 🐳Java基础:Java基础_IT闫的博客-CSDN博客 🐋c语言:c语言_IT闫的博客-CSDN博客 🐟MySQL:…...
WPF组合控件TreeView+DataGrid之DataGrid封装
(关注博主后,在“粉丝专栏”,可免费阅读此文) wpf的功能非常强大,很多控件都是原生的,但是要使用TreeViewDataGrid的组合,就需要我们自己去封装实现。 我们需要的效果如图所示&#x…...

PIL/Pillow
Abstract PIL(Python Imaging Library)是一个用于图像处理的 Python 库。它提供了广泛的功能,包括图像加载、保存、调整大小、裁剪、旋转、滤镜应用等。 由于 PIL 的开发停止在 2009 年,因此推荐使用其后续的维护版本 Pillow。Pillow 是一个兼容 PIL 接…...

ARM 汇编入门
ARM 汇编入门 引言 ARM 汇编语言是 ARM 架构的汇编语言,用于直接控制 ARM 处理器。虽然现代软件开发更多地依赖于高级语言和编译器,但理解 ARM 汇编仍然对于深入了解系统、优化代码和进行低级调试非常重要。本文将为您提供一个简单的 ARM 汇编入门指南…...

SQL进阶:多表查询
在SQL基础部分,我们在讲解的过程中只用到了单表查询。但实际上,常见的业务场景单表查询不能满足,或者拆分查询性能过慢。这个时候我们就需要用到连接查询。即查询多表按一定规则合并后的数据。 注意,合并后的数据也是表ÿ…...
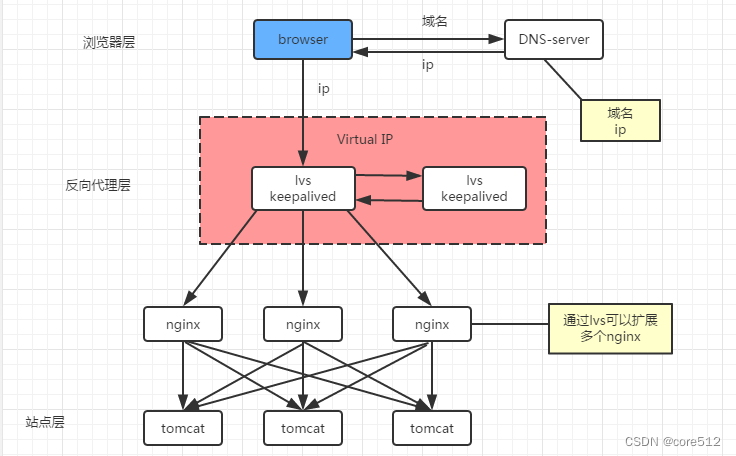
多层负载均衡实现
1、单节点负载均衡 1)站点层与浏览器层之间加入了一个反向代理层,利用高性能的nginx来做反向代理 2)nginx将http请求分发给后端多个web-server 优点: 1)DNS-server不需要动 2)负载均衡:通过ngi…...
Redis取最近10条记录
有时候我们有这样的需求,就是取最近10条数据展示,这些数据不需要存数据库,只用于暂时最近的10条,就没必要在用到Mysql类似的数据库,只需要用redis即可,这样既方便也快! 具体取最近10条的方法&a…...

Mybatis之增删改查
目录 一、引言 二、Mybatis——增 举例:添加用户 三、Mybatis——删 举例:删除用户 四、Mybatis——改 举例:修改用户 五、Mybatis——查 六、注意 END: 一、引言 书接上回,我们在了解完mybatis之后,肯…...

Go 代码检查工具 golangci-lint
一、介绍 golangci-lint 是一个代码检查工具的集合,聚集了多种 Go 代码检查工具,如 golint、go vet 等。 优点: 运行速度快可以集成到 vscode、goland 等开发工具中包含了非常多种代码检查器可以集成到 CI 中这是包含的代码检查器列表&…...

SwiftUI 趣谈之:绝不可能(Never)的 View!
概览 SwiftUI 的出现极大的解放了秃头码农们的生产力。SwiftUI 中众多原生和自定义视图对于我们创建精彩撩人的 App 功不可没! 不过,倘若小伙伴们略微留意过 SwiftUI 框架头文件里的源代码,就会发现里面嵌有一些奇怪 Never 类型,…...

etcd是什么
目录 1.关于etcd2.应用场景 本文主要介绍etcd 概念和基本应用场景。 1.关于etcd etcd是一个开源的、分布式的键值存储系统,用于共享配置和服务发现。它是由CoreOS团队开发的,主要用于实现分布式系统的配置管理和服务发现。 etcd的主要特性包括&#x…...

应用全局的UI状态存储AppStorage
目录 1、概述 2、StorageProp 2.1、观察变化和行为表现 3、StorageLink 3.1、观察变化和行为表现 4、从应用逻辑使用AppStorage和LocalStorage 5、从UI内部使用AppStorage和LocalStorage 6、不建议借助StorageLink的双向同步机制实现事件通知 6.1、推荐的事件通知方式…...

MySQL数据库 触发器
目录 触发器概述 语法 案例 触发器概述 触发器是与表有关的数据库对象,指在insert/update/delete之前(BEFORE)或之后(AFTER),触发并执行触发器中定义的soL语句集合。触发器的这种特性可以协助应用在数据库端确保数据的完整性,日志记录&am…...

C语言学习之给定任意的字符串,清除字符串中的空格
实例要求:给定任意的字符串,清除字符串中的空格,并将其输出;实例分析:1、指针函数实现,需要注意指针函数的返回值是一个指针类型;2、字符类型的数组实现,循环遍历并赋给新的数组&…...

由实验数据进行函数拟合的python实现
0.引言 已知公式求参的过程,对工程而言,一般是一个线性拟合或者非线性拟合的过程。我们现在来以代码片段为例,来描述如何求参。一般这个过程会涉及超定方程的计算。这个过程,原本需要使用matlab,现在python照样可以做…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...
