由实验数据进行函数拟合的python实现
0.引言
已知公式求参的过程,对工程而言,一般是一个线性拟合或者非线性拟合的过程。我们现在来以代码片段为例,来描述如何求参。一般这个过程会涉及超定方程的计算。这个过程,原本需要使用matlab,现在python照样可以做到。
1. 示例1,问题描述
假定我们有一个确定的方程,比如
y = k*x1 + g*x2 /v(x1+x2)
1.1首先我们构建公式本身:
def func(x, k, g, v):(x1, x2) = xseg1 = k*x1;seg2 = g*x2/v*(x1+x2);y = seg1 + seg2;return y;1.2 然后进行实验,采集相关参数:
三个参数,原本三组数据就可以出结果,这就是超定方程的含义。数据点比需要的更多。
#data.csv
14,1 ,3
20,5 ,9
11,7,13
100,9,4
120,8,10
1.3 求解
注意这里的x1,x2组合成一个x参数的过程。它涉及多参数求解的处理。
def CalcParamsOfFun(file_name):# 设置初始参数猜测initial_guess = (1,1,1);# 准备数据filename = "data.csv" # 文件名y = load_csv_data(filename, 0); #yx1 = load_csv_data(filename, 1); #x1x2 = load_csv_data(filename, 2); #x2y_ar = [];for item in y:y_ar.append(item);y = y_ar;x1_data = x1;x2_data = x2;data = (x1_data, x2_data)# 使用curve_fit函数进行拟合popt, pcov = curve_fit(func, data, y_ar, p0=initial_guess)# 显示拟合参数和拟合误差print(popt)print(pcov)return popt;1.4 求解结果识读:
最终popt就是求解出的参数,而剩余的部分pcov是一个协方差矩阵,它反映了整个运算出的参数的不确定度:
[[ 1.55391864e-01 4.35894622e-04 -1.01903114e-03]
[ 4.35894622e-04 4.97531727e-06 2.31409704e-05]
[-1.01903114e-03 2.31409704e-05 3.43718230e-04]]
它的对角线的每一个值,是验算出的参数的可能误差。这里计算出的k的误差有15.5%这是一个比较大的误差,可能对运算精度产生较大影响。矩阵中对角线以外的元素是元素之间的关联关系,较大的值表示两个元素之间可能存在相关性。这里可以看出它们各自的相关性是很小的。
注意,这里的协方差具体数值与公式不符,因为我没有实际制作一笔数据和公式精确匹配。只是用来举例说明。
1.5校验
你可以直观看出公式计算得到的量和实际的数据之间的误差。
def ReCalcCurr_inByCalc(file_name, params):# 准备数据filename = "data.csv" # 文件名y = load_csv_data(filename, 0); #yx1 = load_csv_data(filename, 1); #x1x2 = load_csv_data(filename, 2); #x2y_ar = [];for item in y:y_ar.append(item);y = y_ar;x1_data = x1;x2_data = x2;data = (x1_data, x2_data)for i in np.arange(len(x1_data)):data = (x1_data[i], x2_data[i]);print(func(data, params[0], params[1], params[2]), y[i])相关文章:

由实验数据进行函数拟合的python实现
0.引言 已知公式求参的过程,对工程而言,一般是一个线性拟合或者非线性拟合的过程。我们现在来以代码片段为例,来描述如何求参。一般这个过程会涉及超定方程的计算。这个过程,原本需要使用matlab,现在python照样可以做…...

<JavaEE> 基于 UDP 的 Socket 通信模型
目录 一、认识相关API 1)DatagramSocket 2)DatagramPacket 3)InetSocketAddress 二、UDP数据报套接字通信模型概述 三、回显客户端-服务器通信 1)服务器代码 2)客户端代码 一、认识相关API 1)Data…...

Golang 链表的基础知识
文章目录 链表链表基础知识部分链表的存储方式链表的定义链表的操作性能分析 链表 更多有关于go链表的内容可以见这篇文章链表的创建和读取 链表基础知识部分 什么是链表,链表是一种通过指针串联在一起的线性结构,每一个节点由两部分组成,…...

webpack 常见面试题
1、什么是webpack(必会) webpack是一个打包模块化javascript的工具,在webpack里一切文件皆模块,通过loader转换文件,通过plugin注入钩子,最后输出由多个模块组合成的文件,webpack专注构建模块化…...

three.js实战模拟VR全景视图
文章中使用到的案例图片都来源于:Humus - Textures 里面有很多免费的资源,可以直接下载,每个资源里面都提供6个不同方位的图片,我们通过threejs稍微处理一下,就能实现以下3D效果的场景了。 <template><div …...

聊聊Spring Boot配置文件:优先级顺序、bootstrap.yml与application.yml区别详解
Spring Boot 配置文件 优先级顺序 在Spring Boot中,配置文件的优先级顺序是:bootstrap.yml > application.yml > application-{profile}.yml,其中 {profile} 表示不同的环境配置,如 dev、test、prod 等。当存在相同名称的…...

Milvus向量数据库基础用法及注意细节
1、Milvus数据类型与python对应的数据类型 Milvus Python DataType.INT64 numpy.int64 DataType.INT32 numpy.int32 DataType.INT16 numpy.int16 DataType.BOOL Boolean DataType.FLOAT numpy.float32 DataType.DOUBLE numpy.double DataType.ARRAY list DataT…...

虚拟机多开怎么设置不同IP?虚拟机设置独立IP的技巧
随着虚拟化技术的不断发展,虚拟机已经成为了许多人的必备工具。在虚拟机中,我们可以轻松地创建多个虚拟机,并在每个虚拟机中设置不同的IP地址。下面,我们将介绍如何在虚拟机中设置独立IP地址的方法。 一、虚拟机多开设置不同IP的方…...
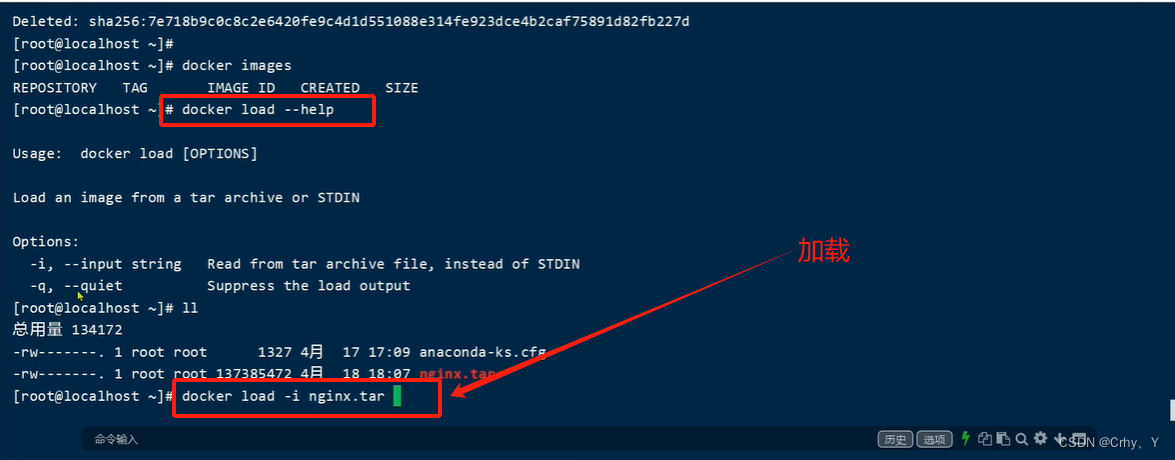
使用Docker-镜像命令
镜像名称一般分两部分组成:[repository]:[tag] 在没有指定tag时,默认是latest,代表最新版本的镜像 目录 案例一:从DockerHub中拉取一个nginx镜像并查看 1.1. 首先去镜像仓库搜索nginx镜像,比如DockerHub 编辑 1.2.操作拉取n…...

4.3 C++对象模型和this指针
4.3 C对象模型和this指针 4.3.1 成员变量和成员函数分开存储 在C中,类内的成员变量和成员函数分开存储 只有非静态成员变量才属于类的对象上 #include <iostream>class Person { public:Person() {mA 0;} //非静态成员变量占对象空间int mA;//静态成员变量…...
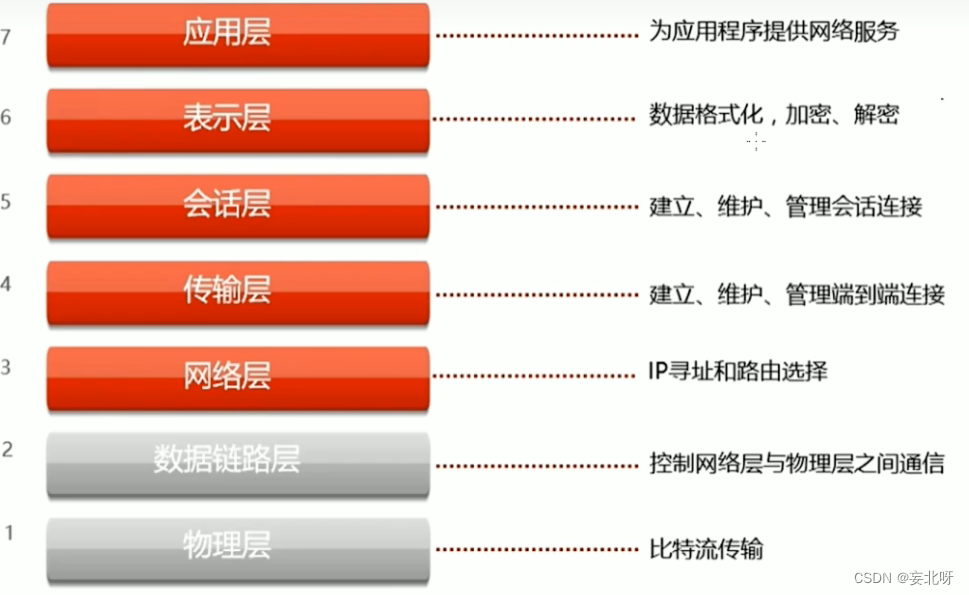
计算机网络——计算机网络的概述(一)
前言: 面对马上的期末考试,也为了以后找工作,需要掌握更多的知识,而且我们现实生活中也已经离不开计算机,更离不开计算机网络,今天开始我们就对计算机网络的知识进行一个简单的学习与记录。 目录 一、什么…...

基于多反应堆的高并发服务器【C/C++/Reactor】(中)ChannelMap 模块的实现
(三)ChannelMap 模块的实现 这个模块其实就是为Channel来服务的,前面讲了Channel这个结构体里边它封装了文件描述符。假如说我们得到了某一个文件描述符,需要基于这个文件描述符进行它对应的事件处理,那怎么办呢&…...

微信小程序实现一个音乐播放器的功能
微信小程序实现一个音乐播放器的功能 要求代码实现wxml 文件wxss 文件js文件 解析 要求 1.页面包含一个音乐列表,点击列表中的音乐可以播放对应的音乐。 2.播放中的音乐在列表中有标识,并且可以暂停或继续播放。 3.显示当前音乐的播放进度和总时长&#…...

算法基础之表达整数的奇怪方式
表达整数的奇怪方式 中国剩余定理: 求M 所有m之积 然后Mi M / mi x 如下图 满足要求 扩展中国剩余定理 找到x **使得x mod mi ai**成立 对于每两个式子 都可以推出①式 即 用扩展欧几里得算法 可以算出k1,-k2和m2–m1 判无解 : 若**(m2–m1) % d ! 0** 说明该等式无解 …...
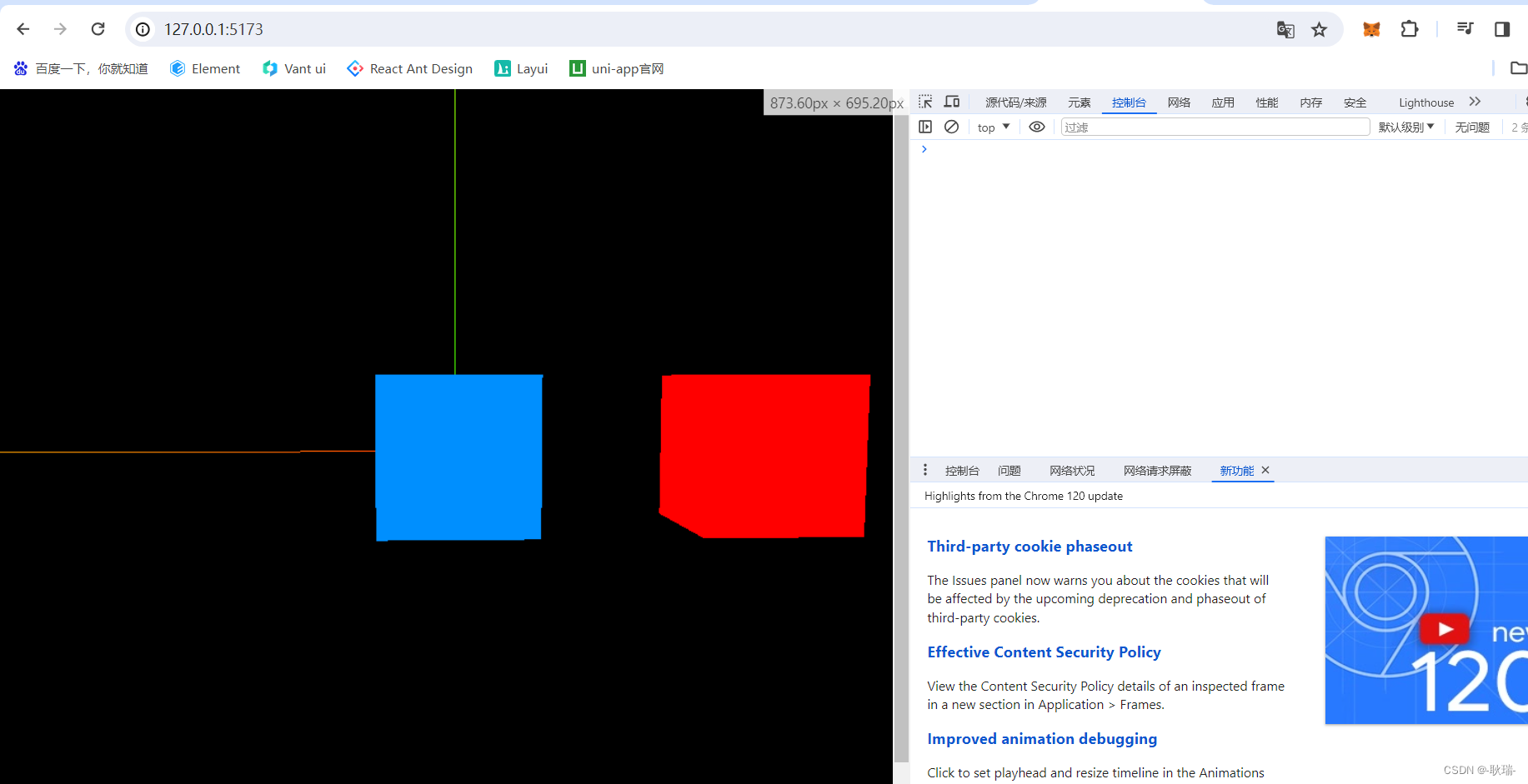
WEB 3D技术 three.js 设置图像随窗口大小变化而变化
本文 我们来讲讲我们图层适应窗口变化的效果 可能这样说有点笼统 那么 自适应应该大家更熟悉 就是 当我们窗口发生变化说 做一些界面调整比例 例如 我们这样一个i项目界面 我们打开 F12 明显有一部分被挡住了 那么 我们可以刷新 这样是正常了 但是 我们将F12关掉 给F12的…...
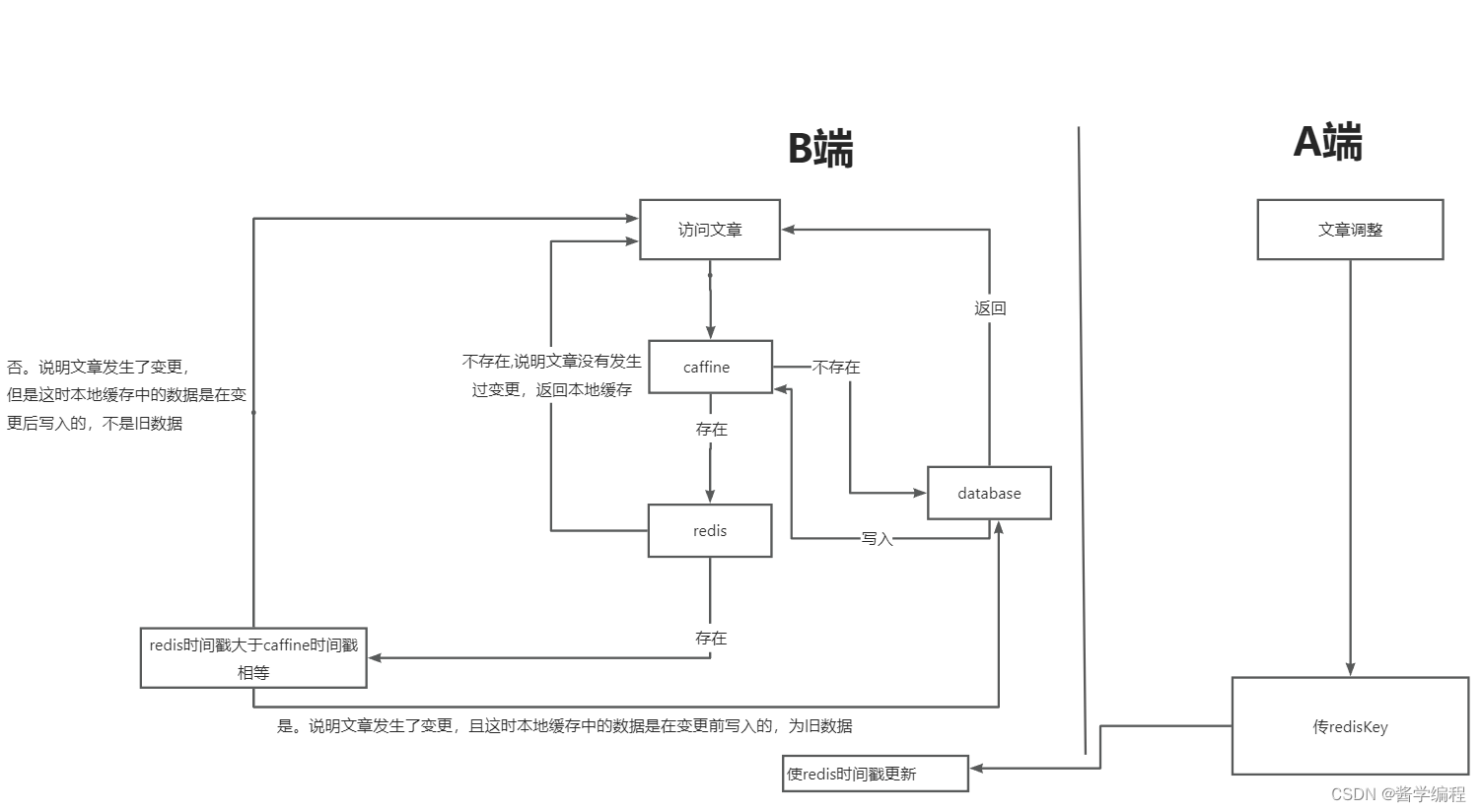
实战案例:缓存不一致问题的解决(redis+本地缓存caffine)
一.问题引入 目前在写项目的时候,在B端查看文章,A端修改文章。为了增加效率,以及防止堆内存溢出,在B端选择本地缓存文章的方案。但是目前出现了A端对文章修改之后,B端读的还是旧数据,出现了缓存不一致的问…...

【开源CDP】市场增长未来的探索,开源CDP带来的技术崛起与变革
数字化趋势之下,数据成了企业竞争的核心资源,不管是公域还是私域,网络俨然成了品牌打响市场的一线战场,然而,在这场数字战役里,许多企业不得不面临一个共同问题:数据零散、分散、平台众多、无法…...
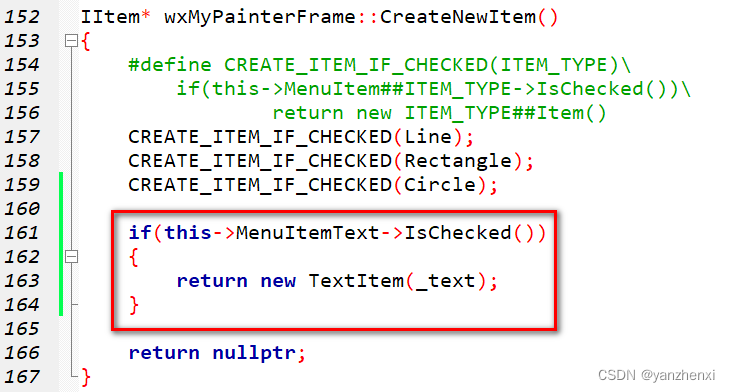
第11章 GUI Page423~424 步骤六 支持文字,使用菜单,对话框输入文字
运行效果: 点击OK,然后再窗口上按住左键,拖动鼠标 关键代码: 新增头文件和成员,新增私有成员_text 成员初始化 为菜单项MenuItemText添加响应函数 新增创建TextItem()的代码...

【Qt】Qt Creator 警告: Unused parameter ‘xxx‘
1. 问题 Qt开发中,有些函数参数没有使用,会报Unused parameter xxx警告,这个警告不影响代码正常运行。 2. 屏蔽这个警告的方法 2.1 方法1 函数中添加 Q_UNUSED(arg); TestClass::TestClass(QObject *parent) {Q_UNUSED(parent); }2.2 方…...

「Vue3面试系列」Vue3.0性能提升主要是通过哪几方面体现的?
文章目录 一、编译阶段diff算法优化静态提升事件监听缓存SSR优化 二、源码体积三、响应式系统参考文献 一、编译阶段 回顾Vue2,我们知道每个组件实例都对应一个 watcher 实例,它会在组件渲染的过程中把用到的数据property记录为依赖,当依赖发…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...

Axure 下拉框联动
实现选省、选完省之后选对应省份下的市区...
