大模型重构云计算:AI原生或将改变格局
摘要:随着AI技术的快速发展,大模型正逐渐改变云计算的格局。本文将深入探讨大模型如何重构云计算,并分析其对云计算的影响。
一、开篇引言
近年来,人工智能技术的飞速发展,特别是大模型的崛起,正在对云计算领域产生深远的影响。在2023百度云智大会·智算大会上,百度集团副总裁侯震宇明确指出:“大模型正在重构云计算”。那么,这一重构具体意味着什么呢?本文将为您详细解读。
二、AI原生云:新格局的崛起
- 深度融合AI与云计算:AI原生云代表了AI技术与云计算技术的深度融合,为用户提供更加智能化、高效的服务。
- 满足高性能需求:随着AI应用的复杂性增加,用户对计算性能、存储和网络的需求也在不断提升。AI原生云正是为了满足这些高性能需求而生。
- 安全与稳定性:AI原生云不仅提供高性能,还确保了数据的安全性和系统的稳定性,为用户提供了更加放心的云计算环境。
三、MaaS:模型即服务,新时代的基石
- 普及AI技术:MaaS将AI模型直接提供给用户,大大降低了AI技术的使用门槛,使得更多的企业和个人可以享受到AI的红利。
- 基础服务的变革:与传统的云计算服务相比,MaaS为用户提供了更加直接、高效的AI解决方案,成为新时代的基础服务。
四、AI原生应用:研发范式的转变
- 数据驱动的研发:AI原生应用更加注重数据的价值,以数据为驱动进行应用的研发和优化。
- 自动化与智能化:借助大模型和AI技术,应用的开发、测试和部署都变得更加自动化和智能化,大大提高了研发效率。
五、结论与展望
大模型重构云计算不仅是技术的变革,更是整个云计算生态的转型。面对这一挑战和机遇,我们需要深入理解和掌握AI技术,以适应这一新时代的到来。展望未来,随着技术的不断进步,我们有理由相信,一个更加智能、高效的云计算时代正在向我们走来。
稿件来源科预云整理而来,如有侵犯你版权的,请来信到邮箱:lizheng@keyu365.com指出,我们将立即改正。
相关文章:

大模型重构云计算:AI原生或将改变格局
摘要:随着AI技术的快速发展,大模型正逐渐改变云计算的格局。本文将深入探讨大模型如何重构云计算,并分析其对云计算的影响。 一、开篇引言 近年来,人工智能技术的飞速发展,特别是大模型的崛起,正在对云计算…...

一文讲清什么是TypeScript装饰器以及如何使用TypeScript装饰器
TypeScript 装饰器是什么? 装饰器(Decorator)是TypeScript提供的一个高级语法,它类似于一种特殊类型的声明,可以附加到类声明,方法,访问符,属性或参数上。装饰器主要以函数的形式出…...
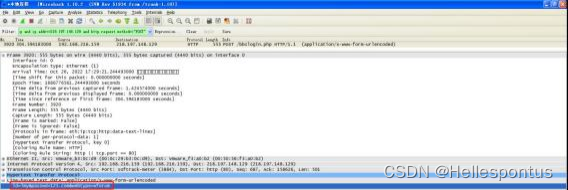
恶意软件样本行为分析——Process Monitor和Wireshark
1.1 实验名称 恶意软件样本行为分析 1.2 实验目的 1) 熟悉 Process Monitor 的使用 2) 熟悉抓包工具 Wireshark 的使用 3) VMware 的熟悉和使用 4) 灰鸽子木马的行为分析 1.3 实验步骤及内容 第一阶段:熟悉 Process Monitor 的使用 利用 Process …...
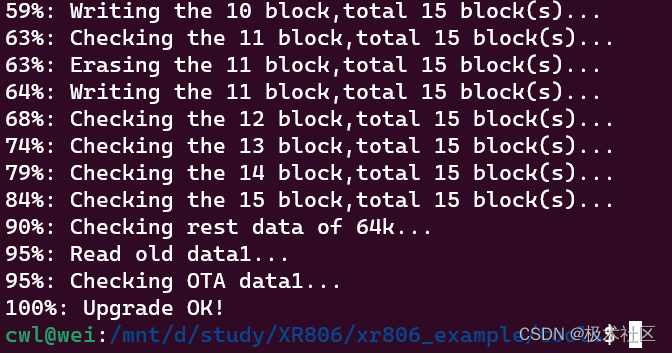
【XR806开发板试用】通过http请求从心知天气网获取天气预报信息
1. 开发环境搭建 本次评测开发环境搭建在windows11的WSL2的Ubuntu20.04中,关于windows安装WSL2可以参考文章: Windows下安装Linux(Ubuntu20.04)子系统(WSL) (1) 在WSL的Ubuntu20.04下安装必要的工具的. 安装git: sudo apt-get install git …...

NPM介绍与使用
什么是NPM? NPM(Node Package Manager)是一个强大的包管理工具,专门用于Node.js应用程序的依赖管理。它允许开发者轻松地分享、安装、更新和管理项目中使用的库、工具和框架。 NPM的安装 在使用NPM之前,请确保你的机…...

servlet +thymeleaf渲染引擎
servlet thymeleaf渲染引擎 一、maven坐标 <dependency><groupId>org.thymeleaf</groupId><artifactId>thymeleaf</artifactId><version>3.0.12.RELEASE</version> <!-- 使用适当的Thymeleaf版本 --> </dependency> &…...

10分钟了解nextTick,并实现简易版本的nextTick
在 Vue.js 中,有一个特殊的方法 nextTick,它在 DOM 更新后执行一段代码,起到等待 DOM 绘制完成的作用。本文会详细介绍 nextTick 的原理和使用方法,并实现一个简易版的 nextTick,加深对它的理解。 一. 什么是 nextTic…...

oracle表空间对象迁移到其他表空间
oracle数据库的磁盘空间满了,除了简单粗暴的增加磁盘空间外,还可以缩小表空间的datafile,因为正常业务运行中,表数据的删除和增加,会造成表空间里面里面有很多空的地方。方案有很多种,我这里简单介绍一下&a…...

<stdlib.h>头文件: C 语言常用标准库函数详解
文章目录 引言1. <stdlib.h> 概览1.1 头文件包含 2. 内存管理函数2.1 malloc 函数2.2 calloc 函数2.3 realloc 函数2.4 free 函数 3. 随机数生成函数3.1 rand 函数3.2 srand 函数 4. 字符串转换函数4.1 atoi 函数4.2 atof 函数4.3 itoa 函数4.4 ltoa 函数4.5 ultoa函数 5…...

Qt前端技术:3.QSS字体样式
small-caps就是让这个文本中的小写字母用大写的形式写出来并且在用大写的形式表达出来后他本身的大小会变小 有绝对尺寸和相对尺寸的区别 绝对尺寸一般是cm,英寸之类的 相对尺寸如px之类的是由显示器的屏幕分辨率来决定的 如windows用户分辨率一般是96像素点每英…...

阿里面试官:面试了一个能力相当不错的候选人,但背调时,他前同事和领导都说他人品很差,纠结该不该要他?...
* 你好,我是前端队长,在职场,玩副业,文末有福利! 在职场中,背调是个躲不开的事情。不管是各行各业背调可能都存在,只是形式不同而已。而且现在大环境不好,可能对个人的要求还更高一些。 背调的主…...

如何设计树形结构
作者简介:大家好,我是smart哥,前中兴通讯、美团架构师,现某互联网公司CTO 联系qq:184480602,加我进群,大家一起学习,一起进步,一起对抗互联网寒冬 前置知识:前…...

限量25台,川崎亮相Ninja ZX-10RR冬季限量款
最近川崎发布了自家ZX-10RR的超级限量版,官方称之为冬季测试版,之前也有一些车型推出过冬季测试版,通常是在年底推出,因为这个时候北半球都是非常寒冷的冬天。 不过这台ZX-10RR冬季测试版,并不仅仅只是限量那么简单&am…...
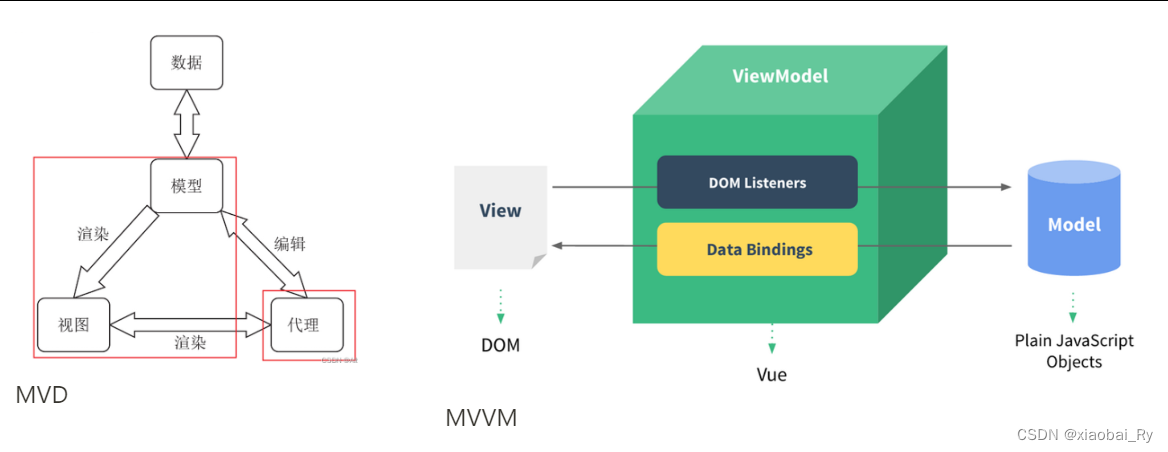
【QT八股文】系列之篇章1 | QT的基础知识及事件/机制
【QT八股文】系列之篇章1 | QT的基础知识及事件/机制 前言0. 基础Qt/PyQt5介绍/关联Qt的优缺点(为什么要用qt来做界面)Qt 的核心机制请简要介绍一下Qt中的主窗口(MainWindow)类,它有哪些重要的函数和成员变量ÿ…...

SpringBoot 3 集成Hive 3
前提条件: 运行环境:Hadoop 3.* Hive 3.* MySQL 8 ,如果还未安装相关环境,请参考:Hive 一文读懂 Centos7 安装Hadoop3 单机版本(伪分布式版本) SpringBoot 2 集成Hive 3 pom.xml <?xml ver…...

STL中优先队列的模拟实现与仿函数的介绍
文章目录 仿函数优先队列的模拟实现 仿函数 上回我们说到,优先队列的实现需要用到仿函数的特性 让我们再回到这里 这里我们发现他传入的用于比较的东西竟然是一个类模板,而不是我们所见到的函数 我们可以先创建一个类,用于比较大小 struc…...
LeetCode刷题--- 目标和
个人主页:元清加油_【C】,【C语言】,【数据结构与算法】-CSDN博客 个人专栏 力扣递归算法题 http://t.csdnimg.cn/yUl2I 【C】 http://t.csdnimg.cn/6AbpV 数据结构与算法 http://t.csdnimg.cn/hKh2l 前言:这个专栏主要讲述递归递归、搜…...
详解(二))
【.NET Core】反射(Reflection)详解(二)
【.NET Core】反射(Reflection)详解(二) 文章目录 【.NET Core】反射(Reflection)详解(二)一、概述二、Type类2.1 Type对象表示哪些类型2.2 获取Type及其关联对象类型的方式2.3 Type…...

【错误记录/js】保存octet-stream为文件后数据错乱
目录 说在前面场景解决方式其他 说在前面 后端:go、gin浏览器:Microsoft Edge 120.0.2210.77 (正式版本) (64 位) 场景 前端通过点击按钮来下载一些文件,但是文件内容是一些非文件形式存储的二进制数据。 后端代码 r : gin.Default()r.Stat…...

sql_lab之sqli中的post注入
Post注入 用burpsuit抓包去做 Post第一关:(gxa5) 1.判断是否存在注入 username1or 11 #&password123&submit%E7%99%BB%E5%BD%95 有回显 username1or 12 #&password123&submit%E7%99%BB%E5%BD%95 没有回显 则证明存在sq…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...
0609)
书籍“之“字形打印矩阵(8)0609
题目 给定一个矩阵matrix,按照"之"字形的方式打印这个矩阵,例如: 1 2 3 4 5 6 7 8 9 10 11 12 ”之“字形打印的结果为:1,…...

相关类相关的可视化图像总结
目录 一、散点图 二、气泡图 三、相关图 四、热力图 五、二维密度图 六、多模态二维密度图 七、雷达图 八、桑基图 九、总结 一、散点图 特点 通过点的位置展示两个连续变量之间的关系,可直观判断线性相关、非线性相关或无相关关系,点的分布密…...
