神经网络:深度学习基础
1.反向传播算法(BP)的概念及简单推导
反向传播(Backpropagation,BP)算法是一种与最优化方法(如梯度下降法)结合使用的,用来训练人工神经网络的常见算法。BP算法对网络中所有权重计算损失函数的梯度,并将梯度反馈给最优化方法,用来更新权值以最小化损失函数。该算法会先按前向传播方式计算(并缓存)每个节点的输出值,然后再按反向传播遍历图的方式计算损失函数值相对于每个参数的偏导数。
接下来我们以全连接层,使用sigmoid激活函数,Softmax+MSE作为损失函数的神经网络为例,推导BP算法逻辑。由于篇幅限制,这里只进行简单推导,后续Rocky将专门写一篇PB算法完整推导流程,大家敬请期待。
首先,我们看看sigmoid激活函数的表达式及其导数:
s i g m o i d 表达式: σ ( x ) = 1 1 + e − x sigmoid表达式:\sigma(x) = \frac{1}{1+e^{-x}} sigmoid表达式:σ(x)=1+e−x1
s i g m o i d 导数: d d x σ ( x ) = σ ( x ) − σ ( x ) 2 = σ ( 1 − σ ) sigmoid导数:\frac{d}{dx}\sigma(x) = \sigma(x) - \sigma(x)^2 = \sigma(1- \sigma) sigmoid导数:dxdσ(x)=σ(x)−σ(x)2=σ(1−σ)
可以看到sigmoid激活函数的导数最终可以表达为输出值的简单运算。
我们再看MSE损失函数的表达式及其导数:
M S E 损失函数的表达式: L = 1 2 ∑ k = 1 K ( y k − o k ) 2 MSE损失函数的表达式:L = \frac{1}{2}\sum^{K}_{k=1}(y_k - o_k)^2 MSE损失函数的表达式:L=21k=1∑K(yk−ok)2
其中 y k y_k yk 代表ground truth(gt)值, o k o_k ok 代表网络输出值。
M S E 损失函数的偏导: ∂ L ∂ o i = ( o i − y i ) MSE损失函数的偏导:\frac{\partial L}{\partial o_i} = (o_i - y_i) MSE损失函数的偏导:∂oi∂L=(oi−yi)
由于偏导数中单且仅当 k = i k = i k=i 时才会起作用,故进行了简化。
接下来我们看看全连接层输出的梯度:
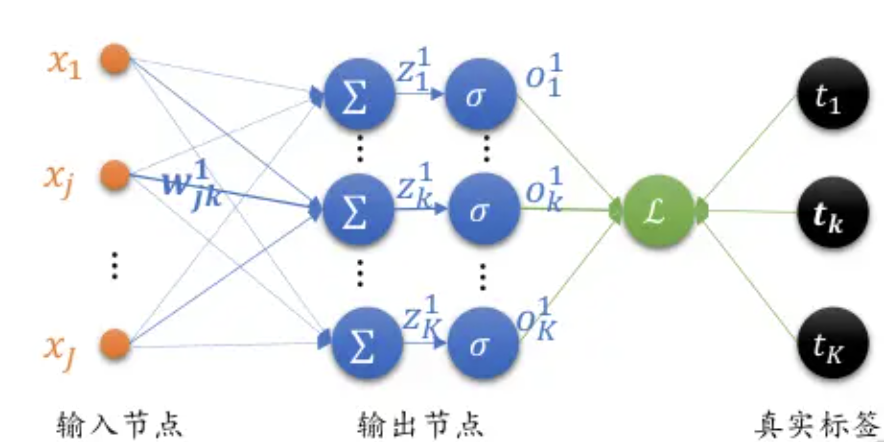
M S E 损失函数的表达式: L = 1 2 ∑ i = 1 K ( o i 1 − t i ) 2 MSE损失函数的表达式:L = \frac{1}{2}\sum^{K}_{i=1}(o_i^1 - t_i)^2 MSE损失函数的表达式:L=21i=1∑K(oi1−ti)2
M S E 损失函数的偏导: ∂ L ∂ w j k = ( o k − t k ) o k ( 1 − o k ) x j MSE损失函数的偏导:\frac{\partial L}{\partial w_{jk}} = (o_k - t_k)o_k(1-o_k)x_j MSE损失函数的偏导:∂wjk∂L=(ok−tk)ok(1−ok)xj
我们用 δ k = ( o k − t k ) o k ( 1 − o k ) \delta_k = (o_k - t_k)o_k(1-o_k) δk=(ok−tk)ok(1−ok) ,则能再次简化:
M S E 损失函数的偏导: d L d w j k = δ k x j MSE损失函数的偏导:\frac{dL}{dw_{jk}} = \delta_kx_j MSE损失函数的偏导:dwjkdL=δkxj
最后,我们看看那PB算法中每一层的偏导数:

输出层:
∂ L ∂ w j k = δ k K o j \frac{\partial L}{\partial w_{jk}} = \delta_k^K o_j ∂wjk∂L=δkKoj
δ k K = ( o k − t k ) o k ( 1 − o k ) \delta_k^K = (o_k - t_k)o_k(1-o_k) δkK=(ok−tk)ok(1−ok)
倒数第二层:
∂ L ∂ w i j = δ j J o i \frac{\partial L}{\partial w_{ij}} = \delta_j^J o_i ∂wij∂L=δjJoi
δ j J = o j ( 1 − o j ) ∑ k δ k K w j k \delta_j^J = o_j(1 - o_j) \sum_{k}\delta_k^Kw_{jk} δjJ=oj(1−oj)k∑δkKwjk
倒数第三层:
∂ L ∂ w n i = δ i I o n \frac{\partial L}{\partial w_{ni}} = \delta_i^I o_n ∂wni∂L=δiIon
δ i I = o i ( 1 − o i ) ∑ j δ j J w i j \delta_i^I = o_i(1 - o_i) \sum_{j}\delta_j^Jw_{ij} δiI=oi(1−oi)j∑δjJwij
像这样依次往回推导,再通过梯度下降算法迭代优化网络参数,即可走完PB算法逻辑。
2.滑动平均的相关概念
滑动平均(exponential moving average),或者叫做指数加权平均(exponentially weighted moving avergae),可以用来估计变量的局部均值,使得变量的更新与一段时间内的历史取值有关。
变量 v v v 在 t t t 时刻记为 v t v_{t} vt , θ t \theta_{t} θt 为变量 v v v 在 t t t 时刻训练后的取值,当不使用滑动平均模型时 v t = θ t v_{t} = \theta_{t} vt=θt ,在使用滑动平均模型后, v t v_{t} vt 的更新公式如下:

上式中, β ϵ [ 0 , 1 ) \beta\epsilon[0,1) βϵ[0,1) 。 β = 0 \beta = 0 β=0 相当于没有使用滑动平均。
t t t 时刻变量 v v v 的滑动平均值大致等于过去 1 / ( 1 − β ) 1/(1-\beta) 1/(1−β) 个时刻 θ \theta θ 值的平均。并使用bias correction将 v t v_{t} vt 除以 ( 1 − β t ) (1 - \beta^{t}) (1−βt) 修正对均值的估计。
加入Bias correction后, v t v_{t} vt 和 v b i a s e d t v_{biased_{t}} vbiasedt 的更新公式如下:

当 t t t 越大, 1 − β t 1 - \beta^{t} 1−βt 越接近1,则公式(1)和(2)得到的结果( v t v_{t} vt 和 v b i a s e d 1 v_{biased_{1}} vbiased1 )将越来越接近。
当 β \beta β 越大时,滑动平均得到的值越和 θ \theta θ 的历史值相关。如果 β = 0.9 \beta = 0.9 β=0.9 ,则大致等于过去10个 θ \theta θ 值的平均;如果 β = 0.99 \beta = 0.99 β=0.99 ,则大致等于过去100个 θ \theta θ 值的平均。
下图代表不同方式计算权重的结果:
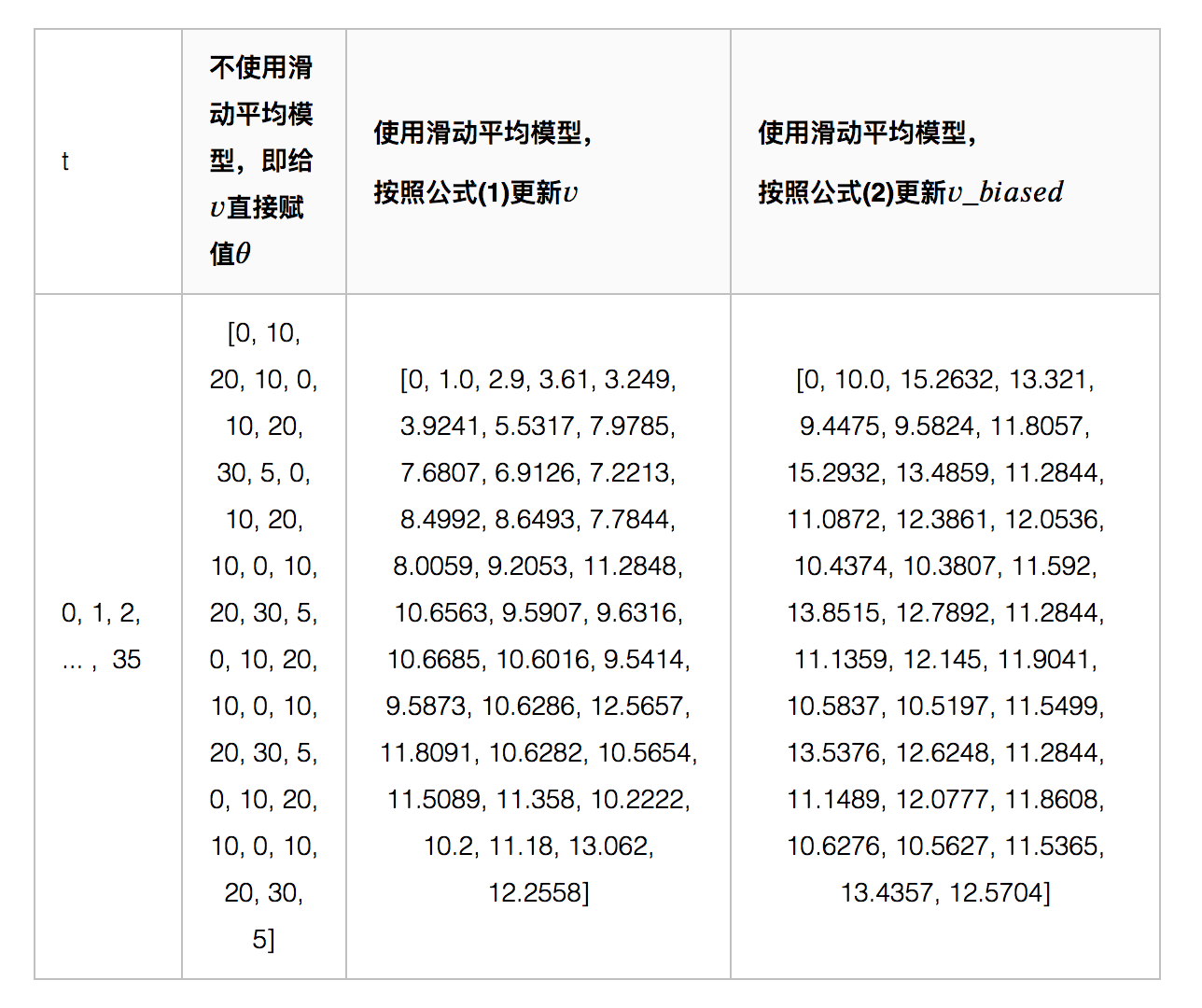
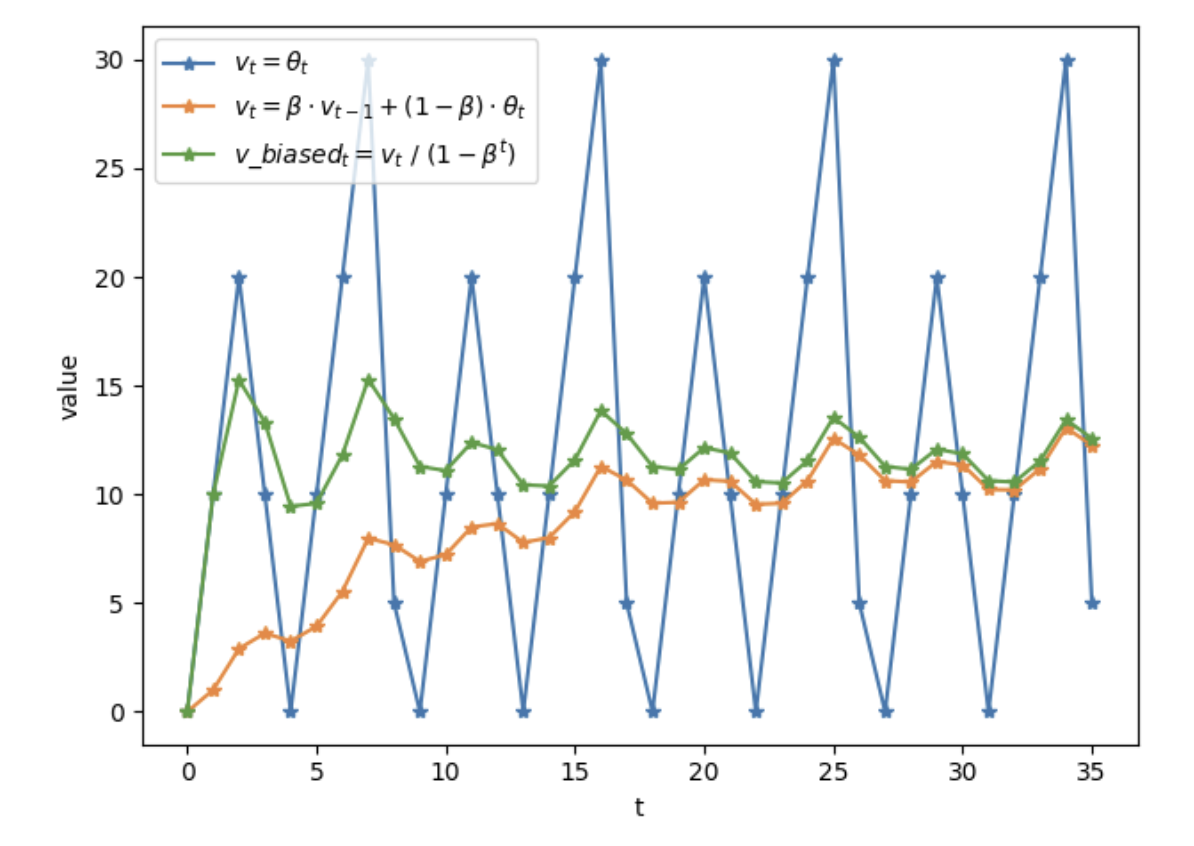
如上图所示,滑动平均可以看作是变量的过去一段时间取值的均值,相比对变量直接赋值而言,滑动平均得到的值在图像上更加平缓光滑,抖动性更小,不会因为某种次的异常取值而使得滑动平均值波动很大。
滑动平均的优势: 占用内存少,不需要保存过去10个或者100个历史 θ \theta θ 值,就能够估计其均值。滑动平均虽然不如将历史值全保存下来计算均值准确,但后者占用更多内存,并且计算成本更高。
为什么滑动平均在测试过程中被使用?
滑动平均可以使模型在测试数据上更鲁棒(robust)。
采用随机梯度下降算法训练神经网络时,使用滑动平均在很多应用中都可以在一定程度上提高最终模型在测试数据上的表现。
训练中对神经网络的权重 w e i g h t s weights weights 使用滑动平均,之后在测试过程中使用滑动平均后的 w e i g h t s weights weights 作为测试时的权重,这样在测试数据上效果更好。因为滑动平均后的 w e i g h t s weights weights 的更新更加平滑,对于随机梯度下降而言,更平滑的更新说明不会偏离最优点很远。比如假设decay=0.999,一个更直观的理解,在最后的1000次训练过程中,模型早已经训练完成,正处于抖动阶段,而滑动平均相当于将最后的1000次抖动进行了平均,这样得到的权重会更加鲁棒。
相关文章:

神经网络:深度学习基础
1.反向传播算法(BP)的概念及简单推导 反向传播(Backpropagation,BP)算法是一种与最优化方法(如梯度下降法)结合使用的,用来训练人工神经网络的常见算法。BP算法对网络中所有权重计算…...
如何在Windows上搭建WebDAV服务并通过内网穿透实现公网访问
文章目录 前言1. 安装IIS必要WebDav组件2. 客户端测试3. 使用cpolar内网穿透,将WebDav服务暴露在公网3.1 安装cpolar内网穿透3.2 配置WebDav公网访问地址 4. 映射本地盘符访问 前言 在Windows上如何搭建WebDav,并且结合cpolar的内网穿透工具实现在公网访…...
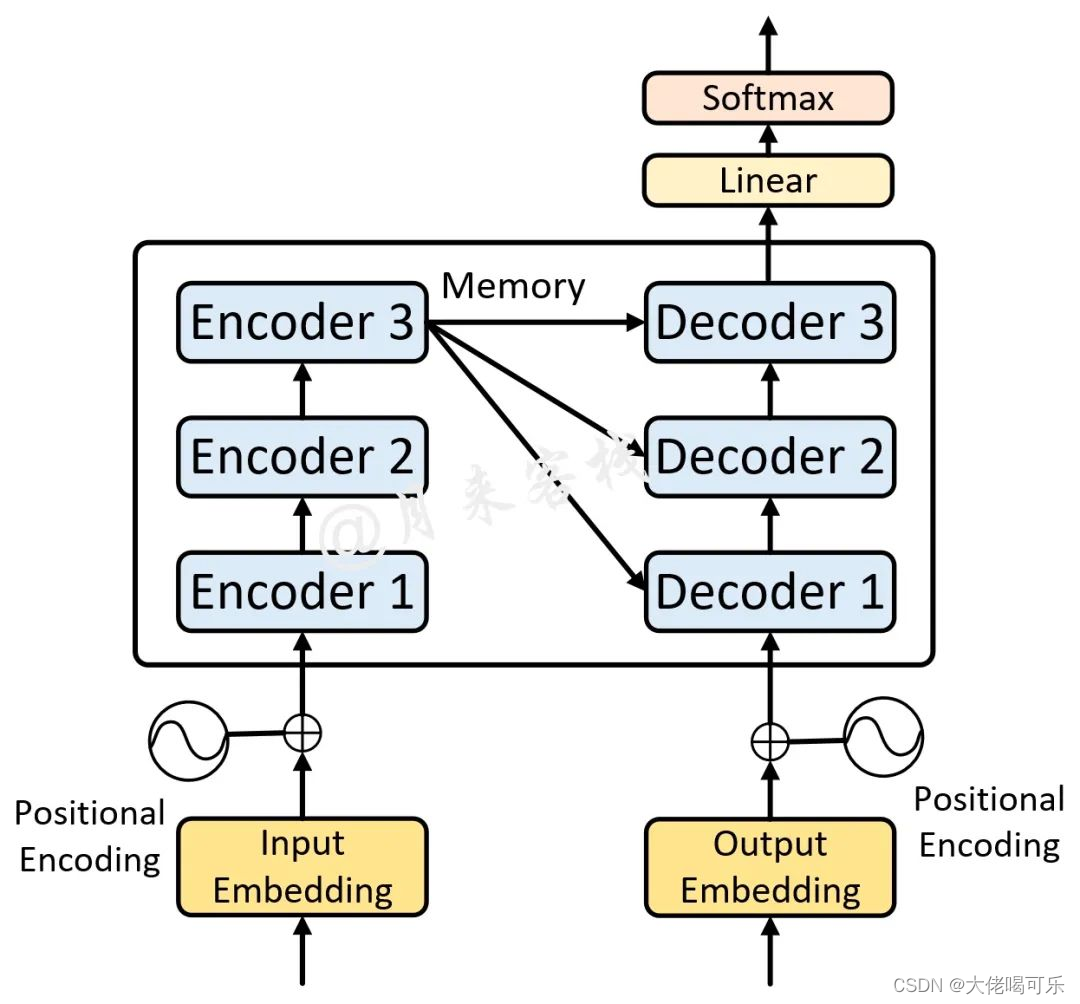
【Transformer框架代码实现】
Transformer Transformer框架注意力机制框架导入必要的库Input Embedding / Out EmbeddingPositional EmbeddingTransformer EmbeddingScaleDotProductAttention(self-attention)MultiHeadAttention 多头注意力机制EncoderLayer 编码层Encoder多层编码块/前馈网络层…...
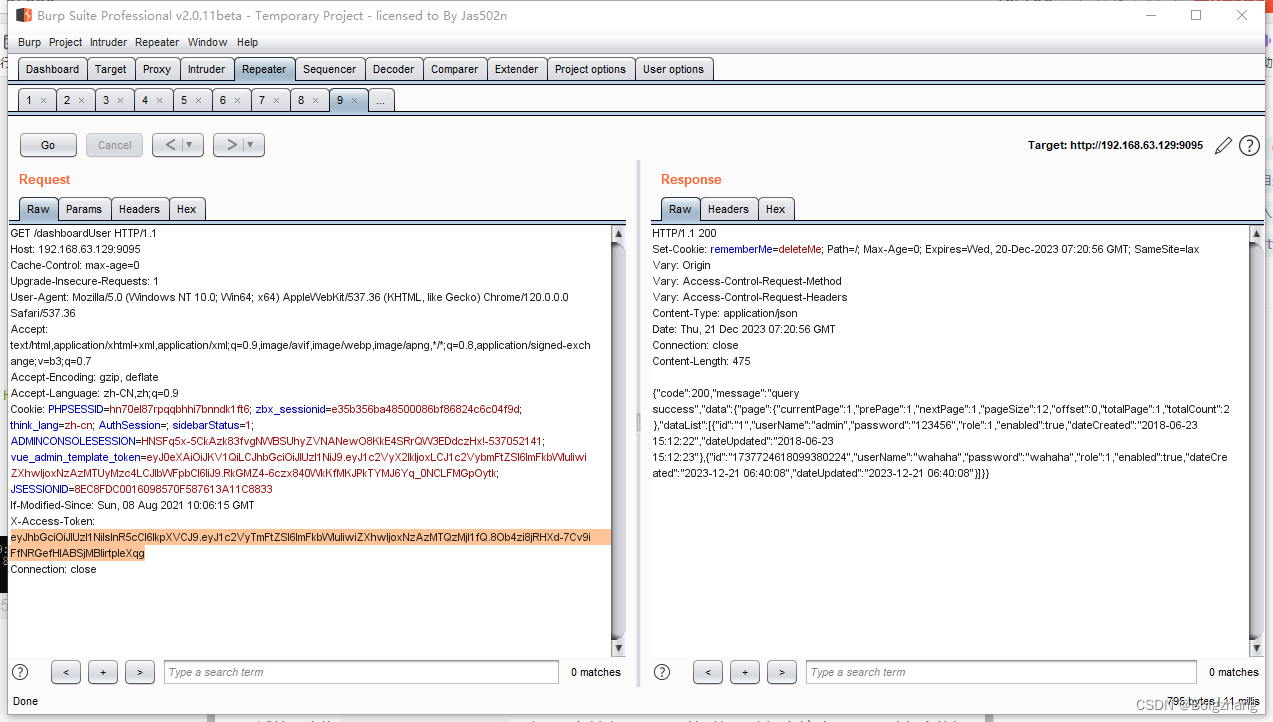
Apache ShenYu 网关JWT认证绕过漏洞 CVE-2021-37580
Apache ShenYu 网关JWT认证绕过漏洞 CVE-2021-37580 已亲自复现 漏洞名称漏洞描述影响版本 漏洞复现环境搭建漏洞利用 修复建议总结 Apache ShenYu 网关JWT认证绕过漏洞 CVE-2021-37580 已亲自复现) 漏洞名称 漏洞描述 Apache ShenYu是一个异步的,高性能的&#x…...

锐捷配置重发布RIP进OSPF中
一、实验拓扑 二、实验目的 使用两种动态路由协议,并使两种协议间的路由可以传递 三、实验配置 第一步:配置全网基本IP R1 Ruijie>enable Ruijie#configure terminal Ruijie(config)#interface gigabitEthernet 0/0 Ruijie(config-if-GigabitEthe…...

Android R修改wifi热点默认为隐藏热点以及禁止自动关闭热点
前言 Android R系统中WLAN 热点设置里面默认是没有wifi热点的隐藏设置选项的,如果默认wifi热点为隐藏热点可以修改代码实现。另外wifi热点设置选项里面有个自动关闭热点,这个选项默认是打开的,有些机器里面配置wifi热点后默认是需要关闭掉的,以免自动关闭后要手动打开。 …...

智能优化算法应用:基于人工大猩猩部队算法3D无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于人工大猩猩部队算法3D无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于人工大猩猩部队算法3D无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.人工大猩猩部队算法4.实验参…...

[JS设计模式]Flyweight Pattern
Flyweight pattern 享元模式是一种结构化的设计模式,主要用于产生大量类似对象而内存又有限的场景。享元模式能节省内存。 假设一个国际化特大城市SZ;它有5个区,分别为nanshan、futian、luohu、baoan、longgang;每个区都有多个图…...
读取配置文件全面总结)
【.Net8教程】(一)读取配置文件全面总结
环境:.net8.0 1. 准备条件 先在appsettings.Development.json或appsettings.json添加配置 添加一个DbOption {"DbOption": {"Conn": "foolishsundaycsdn"} }2.直接读取json配置节点的几种写法 在Main函数中读取json配置 方式一 …...
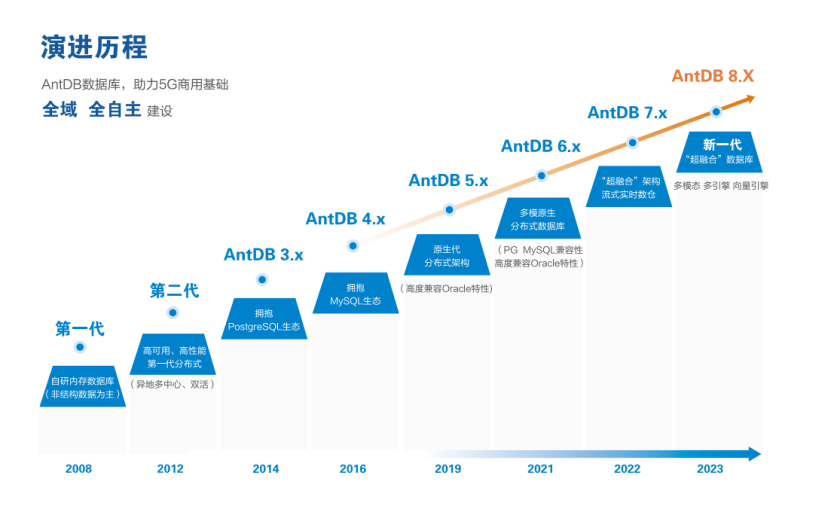
亚信安慧AntDB:支撑中国广电5G业务的数据库之力
自2019年6月获得5G牌照以来,中国广电积极利用700MHz频谱资源,迅速崛起为第四大运营商,标志着其在数字通信领域取得的巨大成就。通过与中国移动紧密合作,共建共享基站已超过400万座,为实现自主运营和差异化竞争提供了坚…...

C++哈希表的实现
C哈希表的实现 一.unordered系列容器的介绍二.哈希介绍1.哈希概念2.哈希函数的常见设计3.哈希冲突4.哈希函数的设计原则 三.解决哈希冲突1.闭散列(开放定址法)1.线性探测1.动图演示2.注意事项3.代码的注意事项4.代码实现 2.开散列(哈希桶,拉链法)1.概念2.动图演示3.增容问题1.拉…...
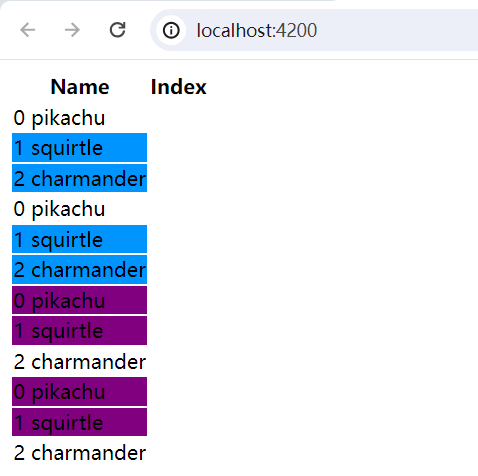
[Angular] 笔记 6:ngStyle
ngStyle 指令: 用于更新 HTML 元素的样式。设置一个或多个样式属性,用以冒号分隔的键值对指定。键是样式名称,带有可选的 .<unit> 后缀(如 ‘top.px’、‘font-style.em’),值为待求值的表达式,得到…...

Linux环境下使用logrotate工具实现nginx日志切割
本文已同步到专业技术网站 www.sufaith.com, 该网站专注于前后端开发技术与经验分享, 包含Web开发、Nodejs、Python、Linux、IT资讯等板块. 一. 前提背景及需求 nginx运行日志默认保存在nginx安装目录下的 /usr/local/nginx/logs 文件夹, 包含access.log和error.log两个文件.…...
数字信号的理解
1 数字信号处理简介 数字信号处理 digital signal processing(DSP)经常与实际的数字系统相混淆。这两个术语都暗示了不同的概念。数字信号处理在本质上比实际的数字系统稍微抽象一些。数字系统是涉及的硬件、二进制代码或数字域。这两个术语之间的普遍混…...

【计算机网络】TCP心跳机制、TCP粘包问题
创作不易,本篇文章如果帮助到了你,还请点赞 关注支持一下♡>𖥦<)!! 主页专栏有更多知识,如有疑问欢迎大家指正讨论,共同进步! 更多计算机网络知识专栏:计算机网络🔥 给大家跳段…...
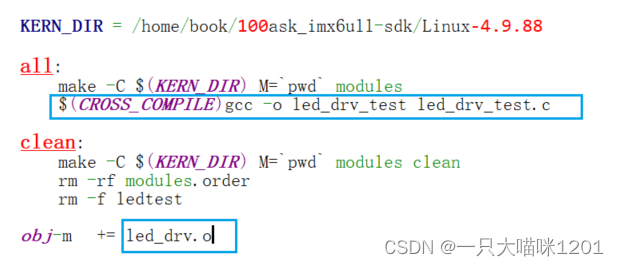
【Linux驱动】字符设备驱动程序框架 | LED驱动
🐱作者:一只大喵咪1201 🐱专栏:《RTOS学习》 🔥格言:你只管努力,剩下的交给时间! 目录 🏀Hello驱动程序⚽驱动程序框架⚽编程 🏀LED驱动⚽配置GPIO⚽编程驱动…...
关于编程网站变成了地方这件事
洛谷: 首页 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) csdn CSDN - 专业开发者社区 力扣 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 常州市力扣紧固件有限公司 常州市 力扣 紧固件 有限公司 博客园 博客园 - 开发…...

stable diffusion工作原理
目录 序言stable diffusion能做什么扩散模型正向扩散逆向扩散 如何训练逆向扩散 Stable Diffusion模型潜在扩散模型变分自动编码器图像分辨率图像放大为什么潜在空间可能存在?在潜在空间中的逆向扩散什么是 VAE 文件? 条件化(conditioning)文本条件化&am…...

华清远见嵌入式学习——ARM——作业2
目录 作业要求: 现象: 代码: 思维导图: 模拟面试题: 作业要求: GPIO实验——3颗LED灯的流水灯实现 现象: 代码: .text .global _start _start: 设置GPIOEF时钟使能 0X50000…...
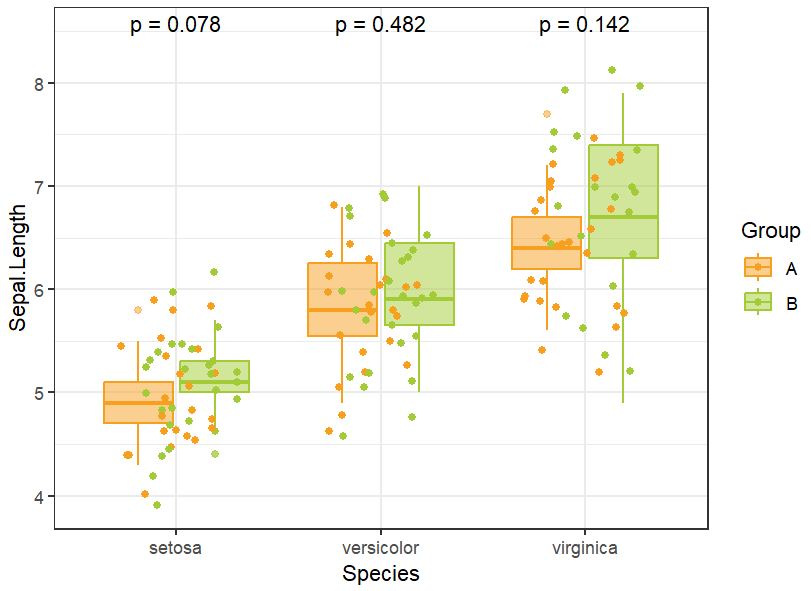
R语言中使用ggplot2绘制散点图箱线图,附加显著性检验
散点图可以直观反映数据的分布,箱线图可以展示均值等关键统计量,二者结合能够清晰呈现数据蕴含的信息。 本篇笔记主要内容:介绍R语言中绘制箱线图和散点图的方法,以及二者结合展示教程,添加差异比较显著性分析…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...

土建施工员考试:建筑施工技术重点知识有哪些?
《管理实务》是土建施工员考试中侧重实操应用与管理能力的科目,核心考查施工组织、质量安全、进度成本等现场管理要点。以下是结合考试大纲与高频考点整理的重点内容,附学习方向和应试技巧: 一、施工组织与进度管理 核心目标: 规…...
