导行电磁波从纵向场分量求其他方向分量的矩阵表示
导行电磁波从纵向场分量求解其他方向分量的矩阵表示
导行电磁波传播的特点
电磁波在均匀、线性、各向同性的空间中沿着 z z z轴传播,可用分离变量法将时间轴、 z z z轴与 x , y x,y x,y轴分离,电磁波的形式可表示为:
E ⃗ = E ⃗ ( x , y ) e − γ z e j ω t H ⃗ = H ⃗ ( x , y ) e − γ z e j ω t \begin{align} \vec E&=\vec E(x,y) \textrm e^{-\gamma z} \textrm e^{j\omega t}\\ \vec H&=\vec H(x,y) \textrm e^{-\gamma z} \textrm e^{j\omega t}\\ \end{align} EH=E(x,y)e−γzejωt=H(x,y)e−γzejωt
纵向场分量的求解导行电磁波的电场和磁场
对于这种波的求解,可以先求出电场、磁场在 z z z轴的分量,然后根据,然后再根据麦克斯韦方程组求出电磁场在 x , y x,y x,y, 由导行电磁波的数学表达式(1), (2)可知, ∂ ∂ z H x = − γ H x \frac{\partial}{\partial z}H_x=-\gamma H_x ∂z∂Hx=−γHx, ∂ ∂ z H y = − γ H y \frac{\partial}{\partial z}H_y=-\gamma H_y ∂z∂Hy=−γHy, ∂ ∂ z E x = − γ E x \frac{\partial}{\partial z}E_x=-\gamma E_x ∂z∂Ex=−γEx, ∂ ∂ z E y = − γ E y \frac{\partial}{\partial z}E_y=-\gamma E_y ∂z∂Ey=−γEy.
从纵向场分量求解其他方向电场和磁场分量及其矩阵表示
麦克斯韦方程组可表示如下:
∇ × H ⃗ = ∂ D ⃗ ∂ t + J ⃗ ∇ × E ⃗ = − ∂ B ⃗ ∂ t ∇ ⋅ D ⃗ = ρ ∇ ⋅ B ⃗ = 0 \begin{align} \nabla \times \vec H &= \frac{\partial \vec D}{\partial t}+\vec J\\ \nabla \times \vec E &= - \frac{\partial \vec B}{\partial t}\\ \nabla \cdotp \vec D &= \rho\\ \nabla \cdotp \vec B &= 0 \end{align} ∇×H∇×E∇⋅D∇⋅B=∂t∂D+J=−∂t∂B=ρ=0
如果已知 H z , E z H_z, E_z Hz,Ez并且知道导行电磁波的形式如公式(1)和(2)所示,并认为传播空间中不存在电荷与电流, J ⃗ = 0 , ρ = 0 \vec J=0, \rho=0 J=0,ρ=0,方程式(3)-(4)可表示为:
∇ × H ⃗ = [ i j k ∂ ∂ x ∂ ∂ y ∂ ∂ z H x H y H z ] = j ω ε E ⃗ ∇ × E ⃗ = [ i j k ∂ ∂ x ∂ ∂ y ∂ ∂ z E x E y E z ] = − j ω μ H ⃗ \begin{align} \nabla \times \vec H &=\begin{bmatrix} i & j & k \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z}\\ H_x &H_y&H_z \end{bmatrix} = j\omega \varepsilon \vec E\\ \nabla \times \vec E &= \begin{bmatrix} i & j & k \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z}\\ E_x &E_y&E_z \end{bmatrix} =- j\omega \mu \vec H\\ \end{align} ∇×H∇×E= i∂x∂Hxj∂y∂Hyk∂z∂Hz =jωεE= i∂x∂Exj∂y∂Eyk∂z∂Ez =−jωμH
将(7)式 x x x 分量展开得到(9),将(8)式 y y y 分量展开得到(10)
∂ ∂ y H z + γ H y = j ω ε E x ∂ ∂ x E z + γ E x = j ω μ H y \begin{align} \frac{\partial}{\partial y}H_z+\gamma H_y &=j\omega \varepsilon E_x\\ \frac{\partial}{\partial x}E_z+\gamma E_x &=j\omega \mu H_y\\ \end{align} ∂y∂Hz+γHy∂x∂Ez+γEx=jωεEx=jωμHy
根据(9)和(10),得到用 H z , E z H_z, E_z Hz,Ez表示的 H y , E x H_y, E_x Hy,Ex:
[ E x H y ] = − 1 k c 2 [ γ j ω μ j ω ε γ ] [ ∂ ∂ x 0 0 ∂ ∂ y ] [ E z H z ] \begin{align} \begin{bmatrix} E_x \\ H_y \end{bmatrix} &= -\frac{1}{k_c^2} \begin{bmatrix} \gamma & j\omega\mu \\ j\omega\varepsilon & \gamma \end{bmatrix} \begin{bmatrix} \frac{\partial}{\partial x} & 0 \\ 0 & \frac{\partial}{\partial y} \end{bmatrix} \begin{bmatrix} E_z \\ H_z \end{bmatrix} \\ \end{align} [ExHy]=−kc21[γjωεjωμγ][∂x∂00∂y∂][EzHz]
将(7)式 y y y 分量展开得到(12),将(8)式 x x x 分量展开得到(13)
− ∂ ∂ x H z − γ H x = j ω ε E y ∂ ∂ y E z + γ E x = j ω μ H x \begin{align} -\frac{\partial}{\partial x}H_z-\gamma H_x &=j\omega \varepsilon E_y\\ \frac{\partial}{\partial y}E_z+\gamma E_x &=j\omega \mu H_x\\ \end{align} −∂x∂Hz−γHx∂y∂Ez+γEx=jωεEy=jωμHx
根据(12)和(13),得到用 H z , E z H_z, E_z Hz,Ez表示的 H x , E y H_x, E_y Hx,Ey:
[ E y H x ] = − 1 k c 2 [ γ − j ω μ − j ω ε γ ] [ ∂ ∂ y 0 0 ∂ ∂ x ] [ E z H z ] \begin{align} \begin{bmatrix} E_y \\ H_x \end{bmatrix} &= -\frac{1}{k_c^2} \begin{bmatrix} \gamma & -j\omega\mu \\ -j\omega\varepsilon & \gamma \end{bmatrix} \begin{bmatrix} \frac{\partial}{\partial y} & 0 \\ 0 & \frac{\partial}{\partial x} \end{bmatrix} \begin{bmatrix} E_z \\ H_z \end{bmatrix} \\ \end{align} [EyHx]=−kc21[γ−jωε−jωμγ][∂y∂00∂x∂][EzHz]
相关文章:

导行电磁波从纵向场分量求其他方向分量的矩阵表示
导行电磁波从纵向场分量求解其他方向分量的矩阵表示 导行电磁波传播的特点 电磁波在均匀、线性、各向同性的空间中沿着 z z z轴传播,可用分离变量法将时间轴、 z z z轴与 x , y x,y x,y轴分离,电磁波的形式可表示为: E ⃗ E ⃗ ( x , y )…...

融资项目——swagger2的注解
1. ApiModel与ApiModelProperty(在实体类中使用) 如上图,ApiModel加在实体类上方,用于整体描述实体类。ApiModelProperty(value"xxx",example"xxx")放于每个属性上方,用于对属性进行描述。swagger2网页上的效果如下图&am…...

【性能优化】MySql数据库查询优化方案
阅读本文你的收获 了解系统运行效率提升的整体解决思路和方向学会MySQl中进行数据库查询优化的步骤学会看慢查询、执行计划、进行性能分析、调优 一、问题:如果你的系统运行很慢,你有什么解决方案? 关于这个问题,我们通常首先…...
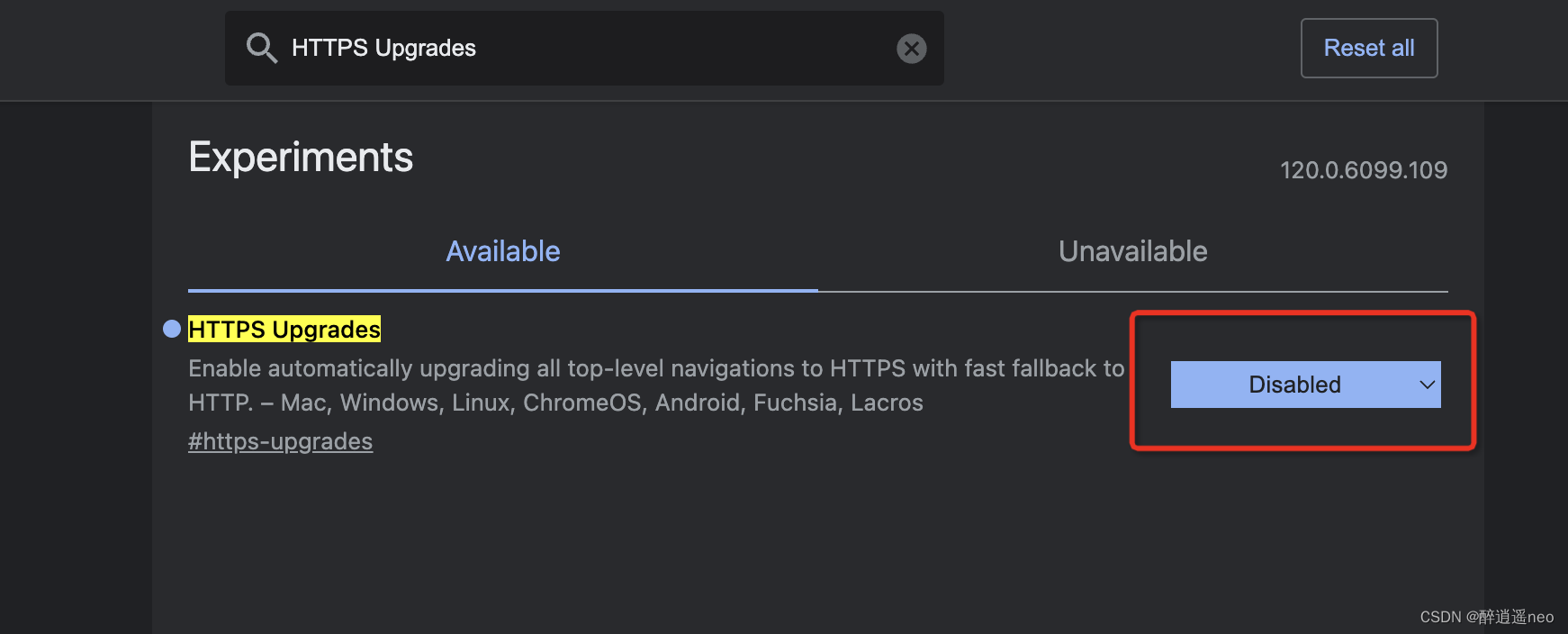
Chrome浏览器http自动跳https问题
现象: Chrome浏览器访问http页面时有时会自动跳转https,导致一些问题。比如: 开发阶段访问dev环境网址跳https,后端还是http,导致接口跨域。 复现: 先访问http网址,再改成https访问…...

【C++进阶02】多态
一、多态的概念及定义 1.1 多态的概念 多态简单来说就是多种形态 同一个行为,不同对象去完成时 会产生出不同的状态 多态分为静态多态和动态多态 静态多态指的是编译时 在程序编译期间确定了程序的行为 比如:函数重载 动态多态指的是运行时 在程序运行…...
PHP开发日志——循环和条件语句嵌套不同,效率不同(循环内加入条件语句,条件语句判断后加入循环,array_map函数中加入条件语句)
十多年前开发框架时,为了效率不断试过各种代码写法,今天又遇到了,想想php8时代会不会有所变化,结果其实也还是和当年一样,但当年没写博客,但现在可以把数据记录下来了。 PHP_loop_ireflies_dark_forest 项目…...
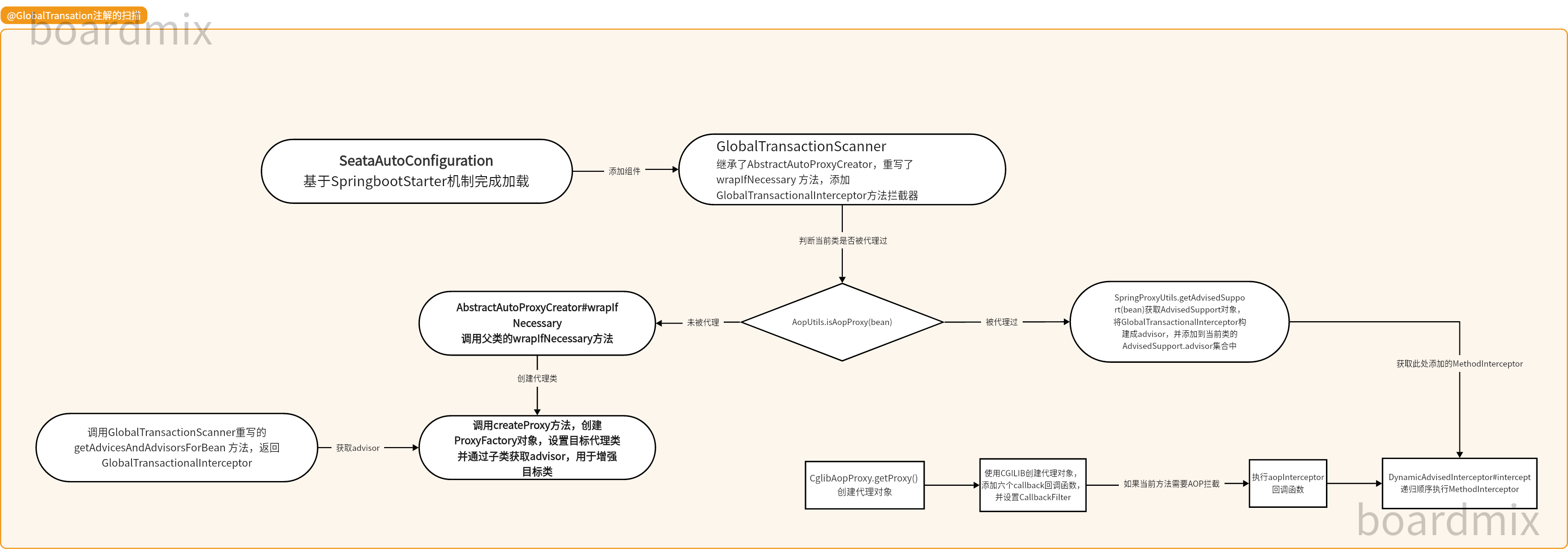
【Seata源码学习 】 扫描@GlobalTransaction注解 篇一
1. SeataAutoConfiguration 自动配置类的加载 基于SpringBoot的starter机制,在应用上下文启动时,会加载SeataAutoConfiguration自动配置类 # Auto Configure org.springframework.boot.autoconfigure.EnableAutoConfigurationio.seata.spring.boot.aut…...
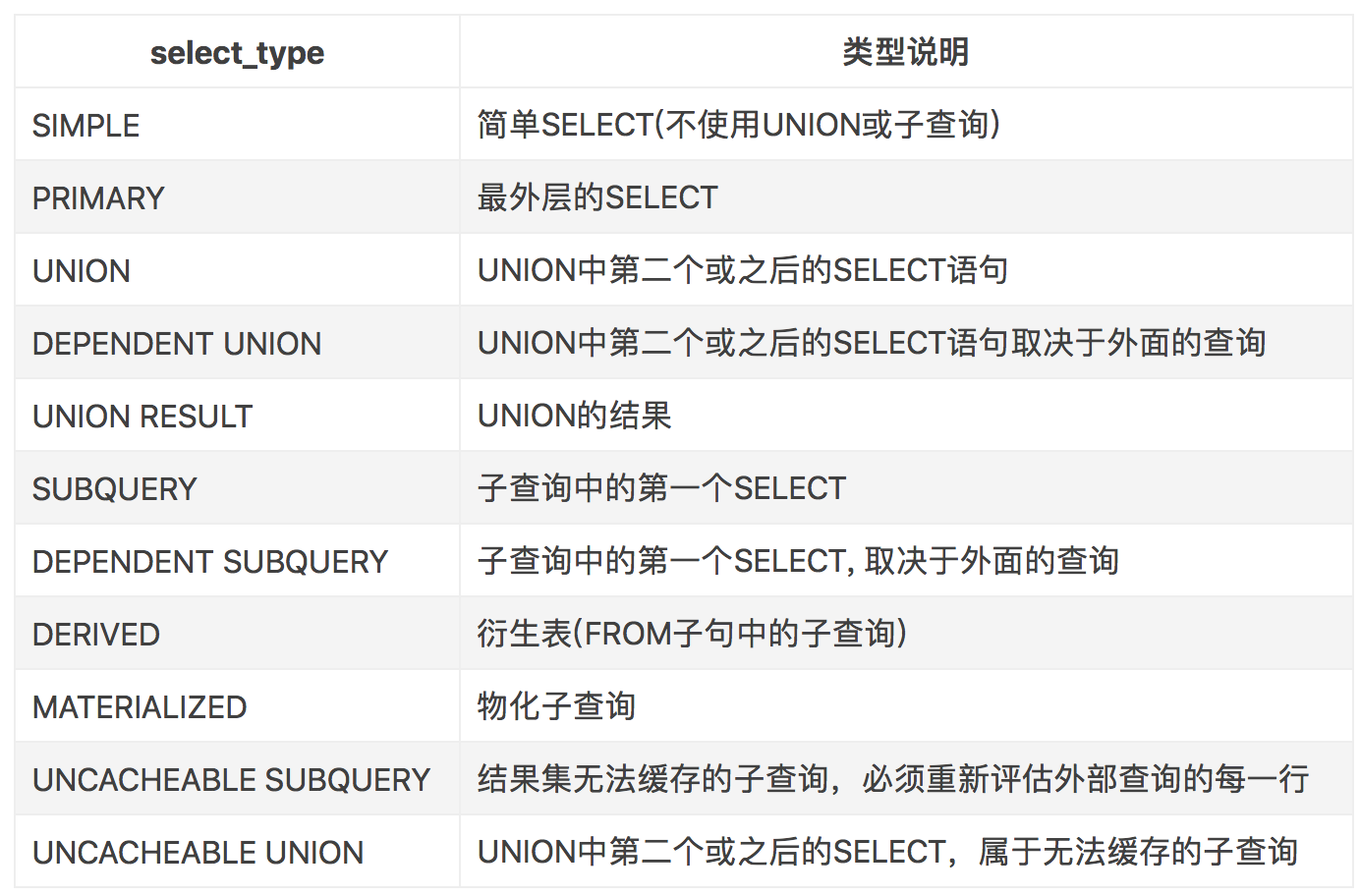
DBA-MySql面试问题及答案-上
文章目录 1.什么是数据库?2.如何查看某个操作的语法?3.MySql的存储引擎有哪些?4.常用的2种存储引擎?6.可以针对表设置引擎吗?如何设置?6.选择合适的存储引擎?7.选择合适的数据类型8.char & varchar9.Mysql字符集10.如何选择…...
网络爬虫之Ajax动态数据采集
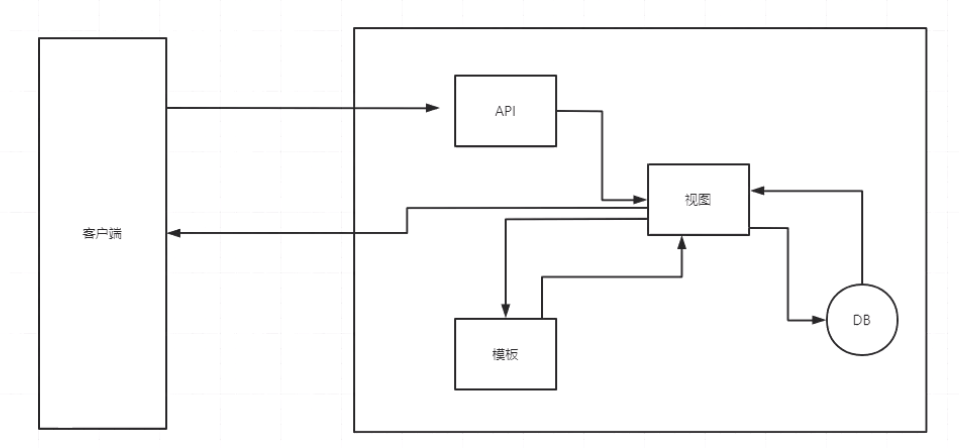
动态数据采集 规则 有时候我们在用 requests 抓取页面的时候,得到的结果可能和在浏览器中看到的不一样,在浏览器中可以看到正常显示的页面教据,但是使用 requests 得到的结果并没有,这是因为requests 获取的都是原始的 HTML 文档…...

c语言的初始学习(练习)
##初学c语言---MOOC浙江大学翁恺先生学习c语言 那么我们先看看这个题目吧,这是初始语法的应用。 记住,我们的程序是按步骤执行的,并不是在不同的两行同时进行。 程序设计:1.了解题目的需要,几个变量需要用到&#x…...

研究论文 2022-Oncoimmunology:AI+癌RNA-seq数据 识别细胞景观
Wang, Xin, et al. "Deep learning using bulk RNA-seq data expands cell landscape identification in tumor microenvironment." Oncoimmunology 11.1 (2022): 2043662. https://www.tandfonline.com/doi/full/10.1080/2162402X.2022.2043662 被引次数࿱…...

ChatGPT4与ArcGIS Pro3助力AI 地理空间分析和可视化及助力科研论文写作
在地学领域,ArcGIS几乎成为了每位科研工作者作图、数据分析的必备工具,而ArcGIS Pro3除了良好地继承了ArcMap强大的数据管理、制图、空间分析等能力,还具有二三维融合、大数据、矢量切片制作及发布、任务工作流、时空立方体等特色功能&#x…...

okhttp系列-一些上限值
1.正在执行的任务数量最大值是64 异步请求放入readyAsyncCalls后,遍历readyAsyncCalls取出任务去执行的时候,如果发现runningAsyncCalls的数量大于等于64,就不从readyAsyncCalls取出任务执行。 public final class Dispatcher {private int …...

C++面向对象(OOP)编程-STL详解(vector)
本文主要介绍STL六大组件,并主要介绍一些容器的使用。 目录 1 泛型编程 2 CSTL 3 STL 六大组件 4 容器 4.1 顺序性容器 4.1.1 顺序性容器的使用场景 4.2 关联式容器 4.2.1 关联式容器的使用场景 4.3 容器适配器 4.3.1 容器适配器的使用场景 5 具体容器的…...

postman几种常见的请求方式
1、get请求直接拼URL形式 对于http接口,有get和post两种请求方式,当接口说明中未明确post中入参必须是json串时,均可用url方式请求 参数既可以写到URL中,也可写到参数列表中,都一样,请求时候都是拼URL 2&am…...
openai最新探索:超级对齐是否可行?
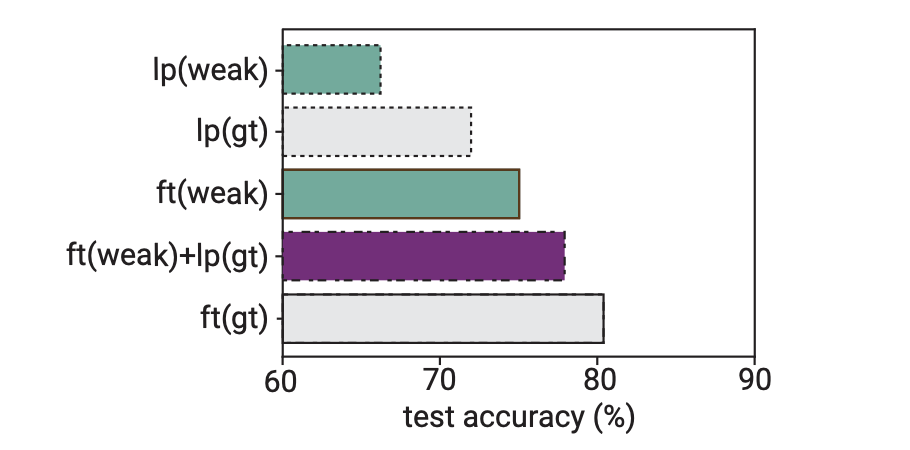
前言 今天来介绍一篇openai最新的paper:弱到强的对齐。 openai专门成立了一个团队来做大模型的超级对齐即superhuman model,之前chatgpt取得成功依赖RLHF即依赖人类反馈,但是作者期望的superhuman model将会是一个能够处理各种复杂问题的强…...

本地websocket服务端结合cpolar内网穿透实现公网访问
文章目录 1. Java 服务端demo环境2. 在pom文件引入第三包封装的netty框架maven坐标3. 创建服务端,以接口模式调用,方便外部调用4. 启动服务,出现以下信息表示启动成功,暴露端口默认99995. 创建隧道映射内网端口6. 查看状态->在线隧道,复制所创建隧道的公网地址加端口号7. 以…...

关于“Python”的核心知识点整理大全37
目录 13.6.2 响应外星人和飞船碰撞 game_stats.py settings.py alien_invasion.py game_functions.py ship.py 注意 13.6.3 有外星人到达屏幕底端 game_functions.py 13.6.4 游戏结束 game_stats.py game_functions.py 13.7 确定应运行游戏的哪些部分 alien_inva…...
Vivado中的FFT IP核使用(含代码)
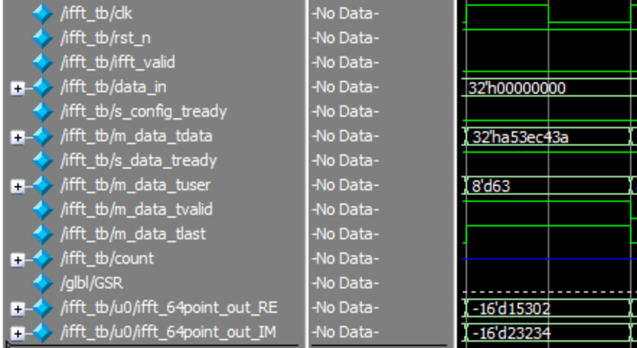
本文介绍了Vidado中FFT IP核的使用,具体内容为:调用IP核>>配置界面介绍>>IP核端口介绍>>MATLAB生成测试数据>>测试verilogHDL>>TestBench仿真>>结果验证>>FFT运算。 1、调用IP核 该IP核对应手册pg109_xfft.pd…...

创新驱动,边缘计算领袖:亚马逊云科技海外服务器服务再进化
2022年亚马逊云科技re:Invent盛会于近日在拉斯维加斯成功召开,吸引了众多业界精英和创新者。亚马逊云科技边缘服务副总裁Jan Hofmeyr在演讲中分享了关于亚马逊云科技海外服务器边缘计算的最新发展和创新成果,引发与会者热烈关注。 re:Invent的核心主题是…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...
