功能强大的开源数据中台系统 DataCap 1.18.0 发布
推荐一套基于 SpringBoot 开发的简单、易用的开源权限管理平台，建议下载使用: https://github.com/devlive-community/authx
推荐一套为 Java 开发人员提供方便易用的 SDK 来与目前提供服务的的 Open AI 进行交互组件：https://github.com/devlive-community/openai-java-sdk
推荐一套全平台数据库管理工具，建议下载使用: https://github.com/devlive-community/dbm
DataCap 发布!
| 发布版本 | 发布时间 |
|---|---|
1.18.0 | 2023-12-22 |
General
- [元数据] 支持克隆行
- [元数据] 支持截断表
- [元数据] 支持刷新数据
- [元数据] 支持删除表
- [元数据] 支持展示表结构
- [元数据] 支持展示表 ER 图
- [元数据] 支持导出表数据
- [元数据] 支持新建表
- [元数据] 支持新建列
- [元数据] 支持删除列
- [查询] 添加自动添加
LIMIT - [用户] 支持用户头像
- [数据源] 优化数据源删除提示信息
- [报表] 支持数据报表功能
- [仪表盘] 支持仪表盘功能
- [数据集] 支持数据集数据
SPI
- 支持 FileSystem
- 支持 Local FileSystem
Docs
- 添加 SDK 使用文档
SqlServer
- 支持多版本
- 修复连接具柄导致连接失败
Pipeline
- 支持 MySQL JDBC 方式
- 支持拖拽构建
Dependencies
- 更新 org.mongodb:mongodb-jdbc
2.0.2到2.0.3 - 更新 ch.qos.logback:logback-classic
1.2.11到1.2.13 - 更新 org.apache.kafka:kafka-clients
2.8.1到3.6.1 - 更新 ch.qos.logback:logback-core
1.2.11到1.2.13 - 更新 com.oracle.database.jdbc:ojdbc8
21.9.0.0到23.3.0.23.09 - 更新 org.elasticsearch.plugin:x-pack-sql-jdbc
7.10.0到8.11.3 - 更新 jackson.version
2.14.2到2.16.0
下载地址
https://datacap.edurt.io/download.html
相关文章：
功能强大的开源数据中台系统 DataCap 1.18.0 发布
推荐一套基于 SpringBoot 开发的简单、易用的开源权限管理平台，建议下载使用: https://github.com/devlive-community/authx 推荐一套为 Java 开发人员提供方便易用的 SDK 来与目前提供服务的的 Open AI 进行交互组件：https://github.com/devlive-commun…...
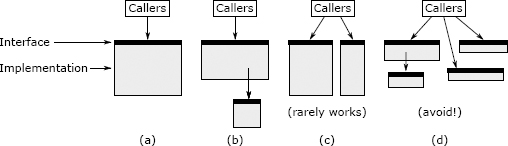
A Philosophy of Software Design 学习笔记
前言 高耦合，低内聚，降低复杂度：在软件迭代中，不关注软件系统结构，导致软件复杂度累加，软件缺乏系统设计，模块混乱，一旦需求增加、修改或者优化，改变的代价无法评估&…...
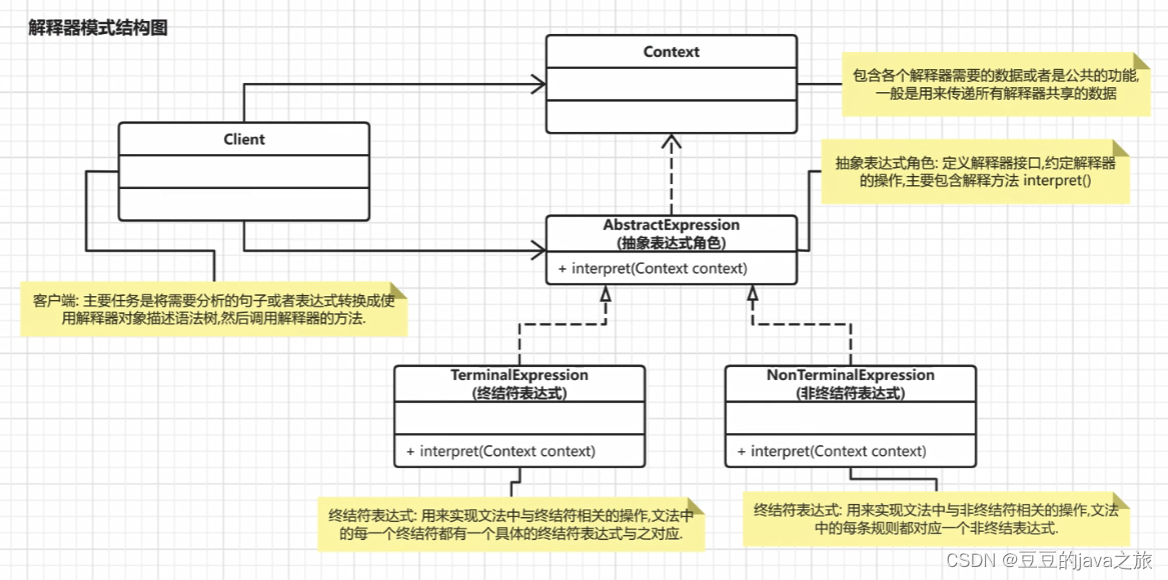
设计模式----解释器模式
一、简介 解释器模式使用频率并不高，通常用来构建一个简单语言的语法解释器，它只在一些非常特定的领域被用到，比如编译器、规则引擎、正则表达式、sql解析等。 解释器模式是行为型设计模式之一，它的原始定义为：用于定义…...
Linux常用命令（一）：Conda、RPM、文件权限、apt-get（更新中...
文章目录 一、Conda二、RPM三、文件权限四、apt-get 一、Conda Conda是一个开源的软件包管理系统和环境管理系统，用于安装和管理软件包及其依赖项。它主要用于Python编程语言，但也可以用于其他语言的项目。Conda可以帮助用户创建不同版本的Python环境&a…...
3 个适用于 Mac 电脑操作的 Android 数据恢复最佳工具 [附步骤]
在当今的数字时代，无论是由于意外删除、系统故障还是其他原因，从 Android 设备中丢失数据不仅会带来不便，而且会造成非常严重的后果。特别是对于Mac用户来说，从Android手机恢复数据是一个很大的麻烦。幸运的是，随着许多…...
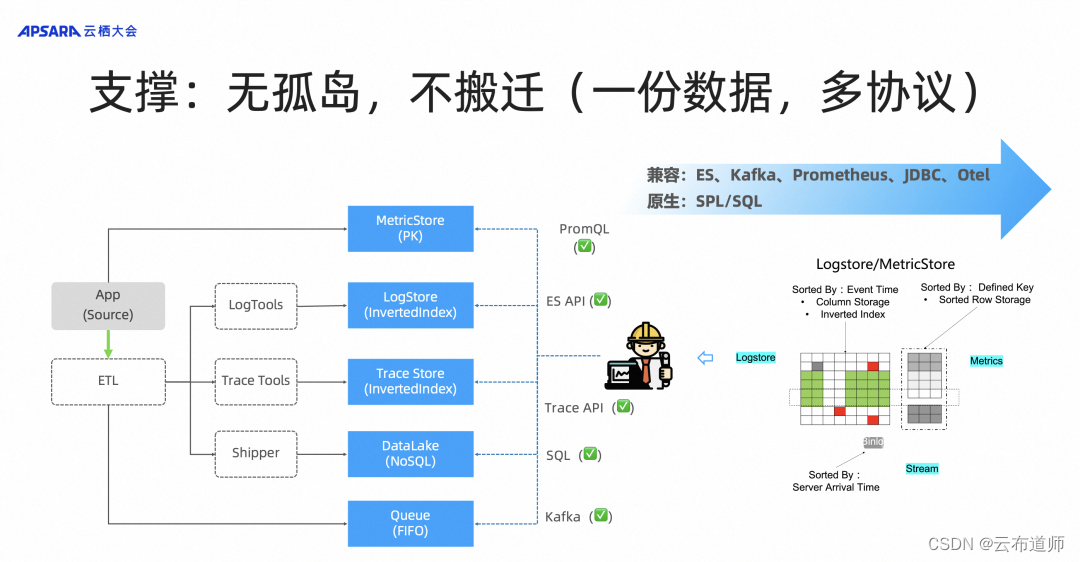
日志服务 SLS 深度解析：拥抱云原生和 AI，基于 SLS 的可观测分析创新
云布道师 10 月 31 日，杭州云栖大会上，日志服务 SLS 研发负责人简志和产品经理孟威等人发表了《日志服务 SLS 深度解析：拥抱云原生和 AI，基于 SLS 的可观测分析创新》的主题演讲，对阿里云日志服务 SLS 产品服务创新以…...
MinIO客户端之rm
MinIO提供了一个命令行程序mc用于协助用户完成日常的维护、管理类工作。 官方资料 mc rm 删除指定的对象。 准备待删除的对象，查看对象，命令如下： ./mc ls local1/bkt2/控制台的输出，如下： [2023-12-16 01:52:54 …...
【Linux笔记】文件和目录操作
🍎个人博客：个人主页 🏆个人专栏：Linux学习 ⛳️ 功不唐捐，玉汝于成 目录 前言 命令 ls (List): pwd (Print Working Directory): cp (Copy): mv (Move): rm (Remove): 结语 我的其他博客 前言 学习Linux命令…...
Vue-router 中hash模式和history模式的区别
Vue-router 中hash模式和history模式的区别 在通过vue-cli创建项目的时候，出现: 于是，去Google一遍。。 vue-router的model有两种模式：hash模式和history模式。 hash模式和history模式的不同 最直观的区别就是在url中 hash 带了一个很丑的…...
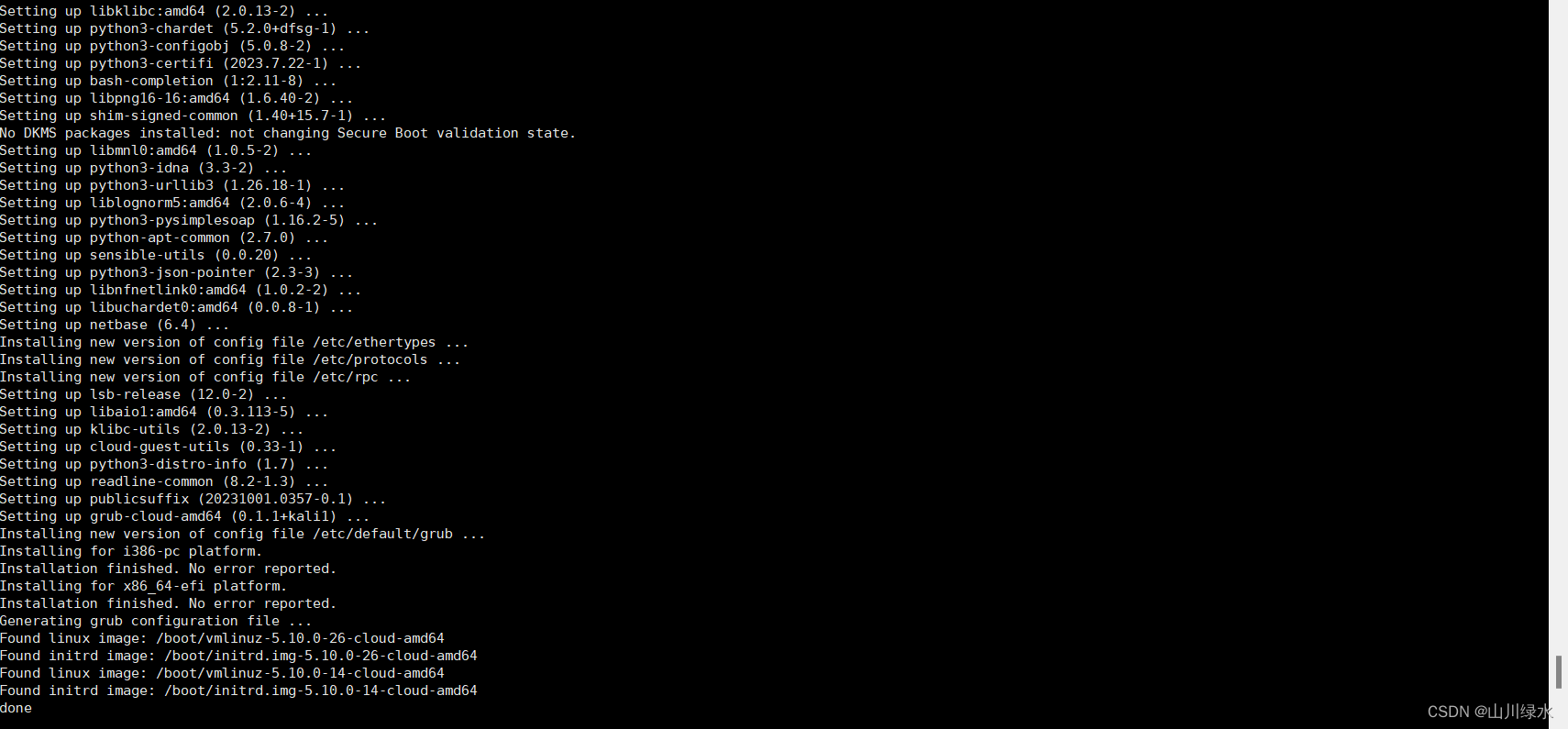
Debian在升级过程中报错
当我们在升级的过程中出现如下报错信息 报错信息如下所示： The following signatures couldnt be verified because the public key is not available: NO_PUBKEY ED444FF07D8D0BF6 W: GPG error: http://mirrors.jevincanders.net/kali kali-rolling InRelease: …...
IOS开发问题记录
1. xcode上传app store connect后testflight没有可构建版本的原因 查看你的邮箱, 里面有原因提示 一般为使用了某些权限, 但是plist没有声明 2. xcode 修改display name后名字并没有改变 原因是并没有修改到plist的CFBundleDisplayName的字段 将CFBundleDisplayName的值修改…...
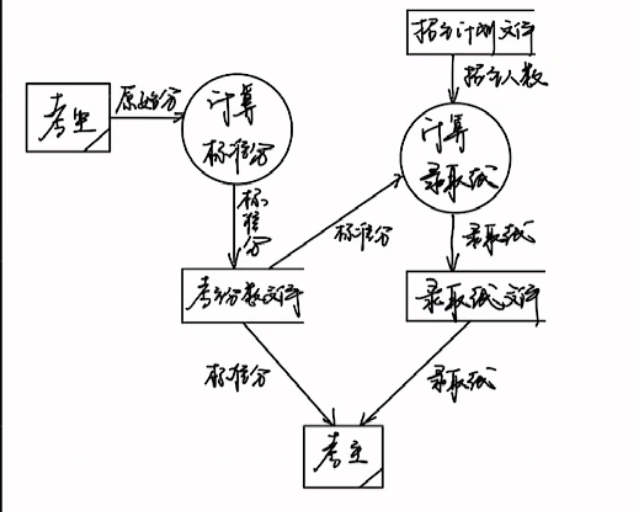
数据流图_DFD图_精简易上手
数据流图(DFD)是一种图形化技术,它描绘信息流和数据从输人移动到输出的过程中所经受的变换。 首先给出一个数据流图样例 基本的四种图形 直角矩形:代表源点或终点,一般来说,是人,如例图的仓库管理员和采购员圆形(也可以画成圆角矩形):是处理,一般来说,是动作,是动词名词的形式…...
使用 Xcode 创建一个新的项目并运行
启动 Xcode: 打开你的 Mac，然后启动 Xcode。你可以在应用程序文件夹中找到它，或者使用 Spotlight 搜索。 创建新项目: 当 Xcode 启动时，选择 “Create a new Xcode project”（创建一个新的 Xcode 项目）。 在项目模板…...
教师未来前景发展
教师是一个光荣而重要的职业，他们承担着培养下一代的责任和使命。随着社会的不断发展和变化，教师的前景也在不断扩大和改变。本文将探讨教师未来的前景发展，并提供一些思考和建议。 首先，教师的就业前景将继续扩大。随着人口的增长…...
【华为机试】2023年真题B卷（python）-采样过滤
一、题目 题目描述： 在做物理实验时，为了计算物体移动的速率，通过相机等工具周期性的采样物体移动能离。由于工具故障，采样数据存在误差甚至相误的情况。需要通过一个算法过滤掉不正确的采样值，不同工具的故意模式存在…...
编译opencv和opencv_contrib
1 下载源码 下载opencv源码https://github.com/opencv/opencv 下载opencv源码https://github.com/opencv/opencv_contrib 2 开始编译 构建需要下载ffmpeg的包，cmake构建时会自动下载，但是比较满，这里可以从下面链接直接下载 https://downloa…...
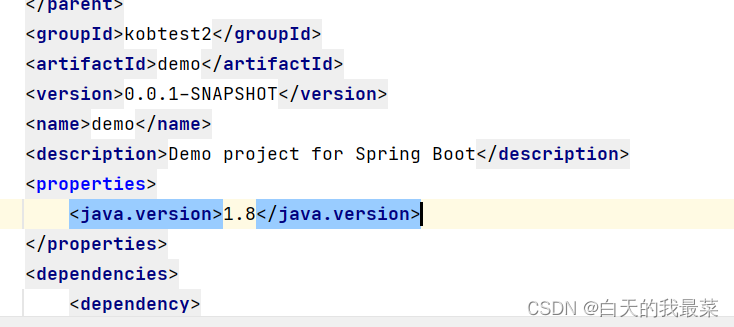
每次maven刷新jdk都要重新设置
pom.xml <java.version>17</java.version> 改为<java.version>1.8</java.version>...
《PySpark大数据分析实战》-18.什么是数据分析
📋 博主简介 💖 作者简介：大家好，我是wux_labs。😜 热衷于各种主流技术，热爱数据科学、机器学习、云计算、人工智能。 通过了TiDB数据库专员（PCTA）、TiDB数据库专家（PCTP…...
【小白攻略】php 小数转为百分比，保留两位小数的函数
php 小数转为百分比 首先，最简单直观的方法是利用PHP内置的number_format函数。该函数可以对一个数字进行格式化，并可以设置小数点后的精度。通过将小数乘以100，再用number_format函数将结果格式化为百分比形式，即可达到将小数转为…...
electron GPU process isn‘t usable. Goodbye
最近再使用electron的时候总是报错打不开，记录一下这个问题的解决方法； // 再主进程中添加下面的即可 app.commandLine.appendSwitch(no-sandbox);官网看了下：https://www.electronjs.org/zh/docs/latest/api/command-line-switches –no-sa…...
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造，完美适配AGV和无人叉车。同时，集成以太网与语音合成技术，为各类高级系统（如MES、调度系统、库位管理、立库等）提供高效便捷的语音交互体验。 L…...
Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...
Xshell远程连接Kali（默认 | 私钥）Note版
前言:xshell远程连接，私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...
React Native 开发环境搭建（全平台详解）
React Native 开发环境搭建（全平台详解） 在开始使用 React Native 开发移动应用之前，正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南，涵盖 macOS 和 Windows 平台的配置步骤，如何在 Android 和 iOS…...
基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能，多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统，涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能，适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...
对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验，以及大语言模型的分析能力，我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际，我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测，聊作存档。等到明…...
Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言，以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天，异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...
CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库，而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例，演示如何： 使用 FetchContent 从 GitH…...
如何理解 IP 数据报中的 TTL？
目录 前言理解 前言 面试灵魂一问：说说对 IP 数据报中 TTL 的理解？我们都知道，IP 数据报由首部和数据两部分组成，首部又分为两部分：固定部分和可变部分，共占 20 字节，而即将讨论的 TTL 就位于首…...
python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同，结合所安装的tensorflow的目录结构修改from语句即可。 原语句： from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后： from tensorflow.python.keras.lay…...