Node.js(二)-模块化
1. 模块化的基本概念
1.1 什么是模块化
模块化是指解决一个复杂问题时,自顶向下逐层将系统拆分成若干模块的过程。对于整个系统来说,模块是可组合、分解和更换的单元。
1.2 编程领域中的模块化
编程领域中的模块化,就是遵守固定的规则,把一个大文件拆成独立并互相依赖的多个小模块。
代码进行模块化拆分的好处:
- 提高了代码的复用性
- 提高了代码的可维护性
- 可以实现按需加载
1.3 模块化规范
模块化规范就是对代码进行模块化的拆分与组合时,需要遵守的那些规则。例如:
- 使用什么样的语法格式来引用模块
- 在模块中使用什么样的语法格式向外暴露成员
- 模块化规范的好处:大家都遵守同样的模块化规范写代码,降低了沟通的成本,极大方便了各个模块之间的相互调用利人利己。
2. Node.js中的模块化
2.1 Node.js中模块的分类
Node.js 中根据模块来源的不同,将模块分为了3大类,分别是:
- 内置模块(内置模块是由 Node.js 官方提供的,例如 fs、path、http 等)
- 自定义模块 (用户创建的每个.js 文件,都是自定义模块)
- 第三方模块(由第方三开发出来的模块,并非官方提供的内置模块,也不是用户创建的自定义模块,使用前需要先下载
2.2 加载模块
使用强大的require()方法,可以加载需要的内置模块、自定义模块、第三方模块进行使用,例如:
// 1.加载内置的fs模块
const fs = require('fs')// 2.加载用户自定义模块
const custom = require('./custom.js')// 3.加载第三方模块
const moment = require('moment')注意:1.使用require()方法加载其他模块时,会执行被加载模块中的代码;2.使用require()方法加载自定义模块时,可以省略 .js的后缀名。
2.3 Node.js中的模块作用域
2.3.1 什么是模块作用域
和函数作用域类似,在自定义模块中定义的变量、方法等成员,只能在当前模块内被访问,这种模块级别的访问限制,叫做模块作用域。
// 这是01-模块化作用域.js
const userName = '张三'function sayHello(){console.log('大家好,我是:'+userName);
}// 这是02-test.js
const custom = require('./01-模块作用域')console.log('custom ',custom );//输出:custom {}2.3.2 模块作用域的好处
防止污染全局变量
2.4 向外共享模块作用域成员
2.4.1 module
在每个 .js 自定义模块中都有一个 module 对象,它里面存储了和当前模块有关的信息,打印如下:
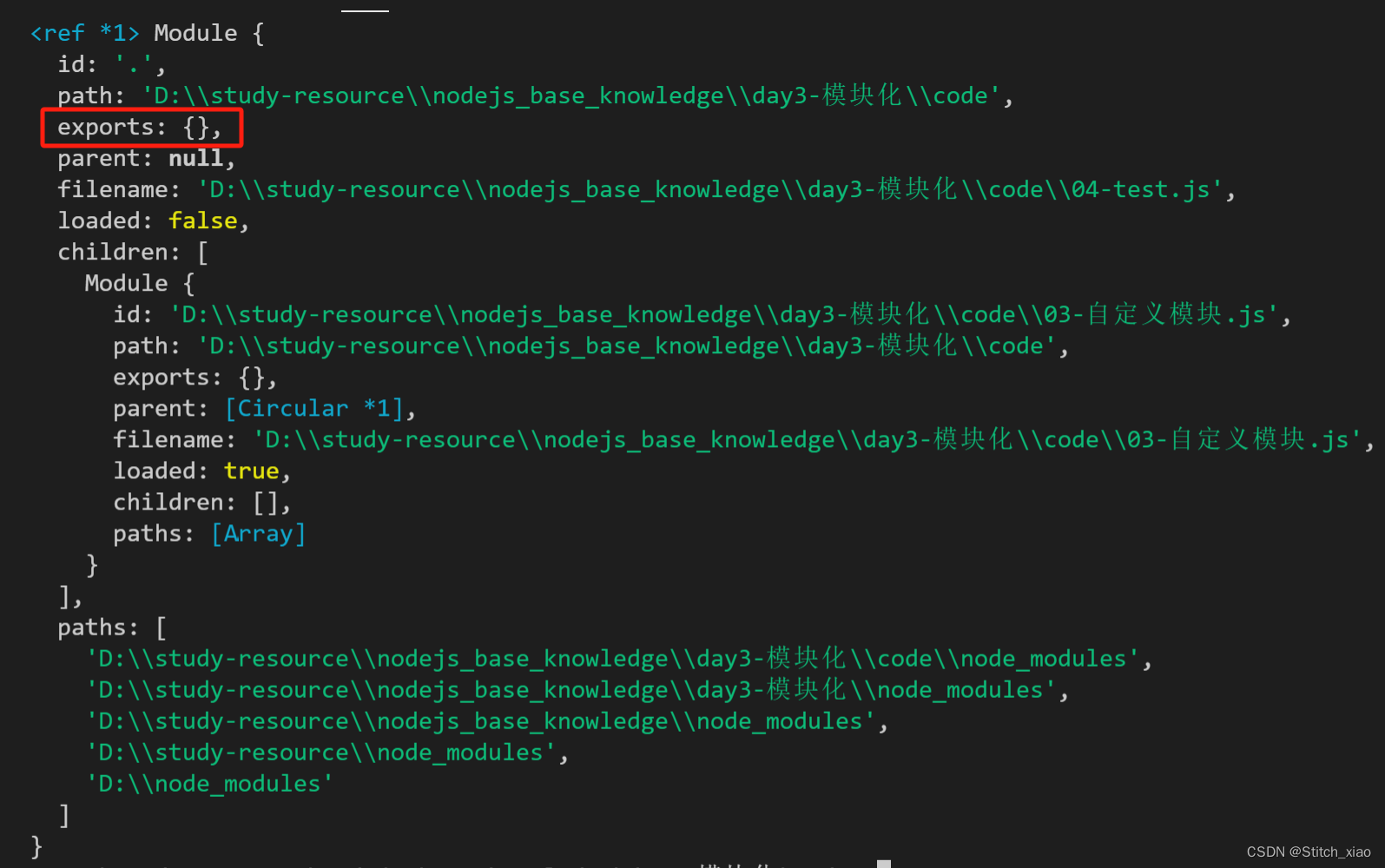
2.4.2 module.exports
在自定义模块中,可以使用 module.exports 对象,将模块内的成员共享出去,供外界使用。外界用 require()方法导入自定义模块时,得到的就是module.exports 所指向的对象。
2.4.3 共享成员时的注意点
使用require方法导入模块时,永远以module.exports指向的对象为准。
2.4.4 exports对象
由于 module.exports 单词写起来比较复杂,为了简化向外共享成员的代码,Node 提供了 exports 对象。默认情况下,exports 和 module.exports 指向同一个对象。最终共享的结果,还是以 module.exports 指向的对象为准。
 2.4.5 exports和module.exports的使用误区
2.4.5 exports和module.exports的使用误区
时刻谨记,require() 模块时,得到的永远是 module.exports 指向的对象(图来自于黑马程序员课程PPT,因为这段犯懒没动手):

原理图:

注意:为了防止混乱,建议大家不要在同一个模块中同时使用 exports 和 module.exports。
2.5 Node.js中的模块化规范
Node.js遵循了CommonJS模块化规范,CommonJS规范了模块的特性和各模块之间如何相互依赖。
CommonJS 规定:
- ①每个模块内部,module 变量代表当前模块。
- ②module 变量是一个对象,它的 exports 属性(即 module.exports)是对外的接口。
- ③加载某个模块,其实是加载该模块的 module.exports 属性。require() 方法用于加载模块。
相关文章:

Node.js(二)-模块化
1. 模块化的基本概念 1.1 什么是模块化 模块化是指解决一个复杂问题时,自顶向下逐层将系统拆分成若干模块的过程。对于整个系统来说,模块是可组合、分解和更换的单元。 1.2 编程领域中的模块化 编程领域中的模块化,就是遵守固定的规则&…...
)
ARM AArch64的TrustZone架构详解(上)
目录 一、概述 1.1 在开始之前 二、什么是TrustZone? 2.1 Armv8-M的TrustZone 2.2 Armv9-A Realm Management Extension(RME)...
的构想)
从源PC上一次性p2v(qcow2)的构想
磁盘分区表,虚拟硬盘文件,操作系统引导 1. 基本概念和术语 源硬盘:一般就是客户的PC机的硬盘,硬盘里面包含了Windows分区。 源Windows:以源硬盘启动的Windows环境。 虚拟磁盘文件:文件格式有qcow2、vhd…...

数据结构:KMP算法
1.何为KMP算法 KMP算法是由Knuth、Morris和Pratt三位学者发明的,所以取了三位学者名字的首字母,叫作KMP算法。 2.KMP的用处 KMP主要用于字符串匹配的问题,主要思想是当出现字符串不匹配时,我们可以知道一部分之前已经匹配过的的文…...
小程序真机如何清除订阅数据
在做小程序订阅消息开发的过程中发现,真机上如果是选择了‘总是保持以上选择’,一旦用户授权后,后面就不会再弹出申请改订阅消息的授权弹窗,这对于开发过程中是很不方便的。 曾试过清除缓存,重进小程序也不能清除掉 解…...
基于ssm出租车管理系统的设计与实现论文
摘 要 现代经济快节奏发展以及不断完善升级的信息化技术,让传统数据信息的管理升级为软件存储,归纳,集中处理数据信息的管理方式。本出租车管理系统就是在这样的大环境下诞生,其可以帮助管理者在短时间内处理完毕庞大的数据信息&…...

音视频转码
音视频转码是指: 容器中音视频数据编码方式转换,如由H.264编码转成mpeg-4编码,mp3转成AAC;音视频码率的转换,如4Mb视频码率降为2Mb,视频分辨率的转换,如1080P转换为720P,音频重采样…...
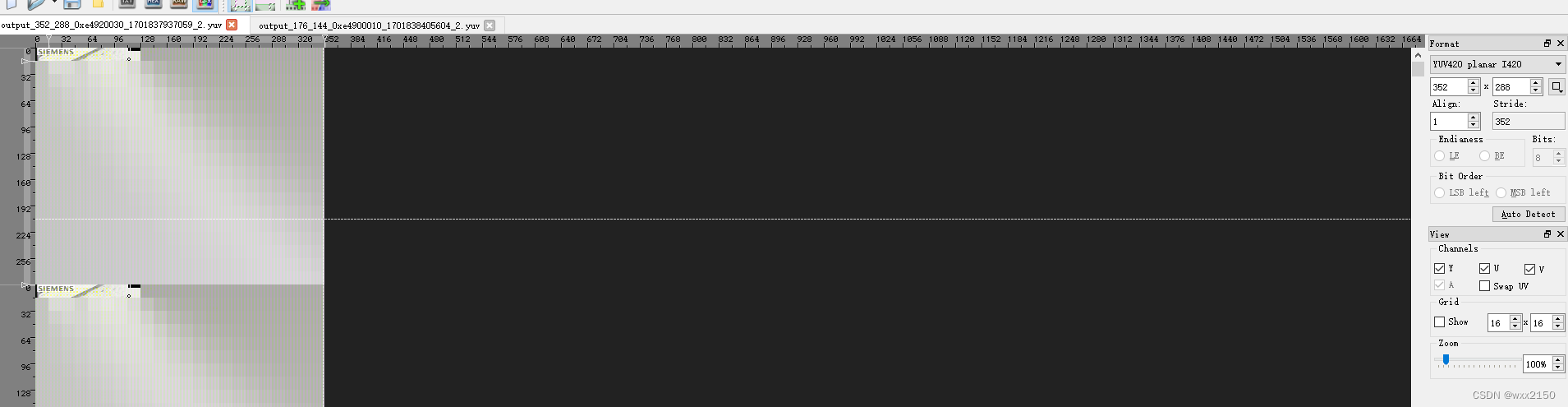
编解码异常分析
前言 最近在做的项目,有H264解码的需求。部分H264文件解码播放后,显示为绿屏或者花屏。 分析 如何确认是否是高通硬解码的问题 adb 指令 adb root adb remount adb shell setenforce 0 adb shell setprop vendor.gralloc.disable_ubwc 1 adb shell c…...

APISpace 热门好用的API推荐,含免费次数
短信验证码:可用于登录、注册、找回密码、支付认证等等应用场景。支持三大运营商,3秒可达,99.99%到达率,支持大容量高并发。通知短信:短信通知支持三大运营商以及虚拟运营商,我们提供电信级运维…...
)
Qt/QML编程学习之心得:一个.qml文件调用另一个.qml文件(十七)
在c++中,一个文件调用另外一个文件最直接最快捷的方式就是#incldue<头文件>的使用,那么在元数据描述性语言QML中,如何从一个界面描述调用另外一个界面描述,一个.qml文件调用另外一个.qml呢?QML虽然有个import,但是用法可以说完全不同于#include。 引用方法1:直接…...

C++_单列模式介绍
介绍 (1)…什么是单例 1.只能有一个实例化的对象的类(2).单例有什么用 1.多线程的线程池的设计 2.系统中只需要一个窗口时才使用单例(无法重复创建) 3.一个操作系统只能有一个文件系统(3).单例怎么用 1.隐藏所有构造函数 2.静态成员内部调用构造函数实例化 3.提供一个静态函数来…...

油烟净化器如何做到高效净化?科技力量,清新餐饮生活
我最近分析了餐饮市场的油烟净化器等产品报告,解决了餐饮业厨房油腻的难题,更加方便了在餐饮业和商业场所有需求的小伙伴们。 油烟净化器的出现,为我们的餐饮生活注入了一抹清新的色彩。然而,它究竟是如何工作的?为何能…...

【HTML5】HTML5 语音合成
一、前言 前一段时间在项目中需要用到播报文字语音。找到了 HTML 5 有这样的功能。 现在有时间进行总结下。 二、SpeechSynthesis SpeechSynthesis 接口是语音服务的控制接口。它可以用于获取设备上关于可用的合成声音的信息, 开始、暂停语音,或者别…...

顺序表的实现
目录 一. 数据结构相关概念 二、线性表 三、顺序表概念及结构 3.1顺序表一般可以分为: 3.2 接口实现: 四、基本操作实现 4.1顺序表初始化 4.2检查空间,如果满了,进行增容编辑 4.3顺序表打印 4.4顺序表销毁 4.5顺…...
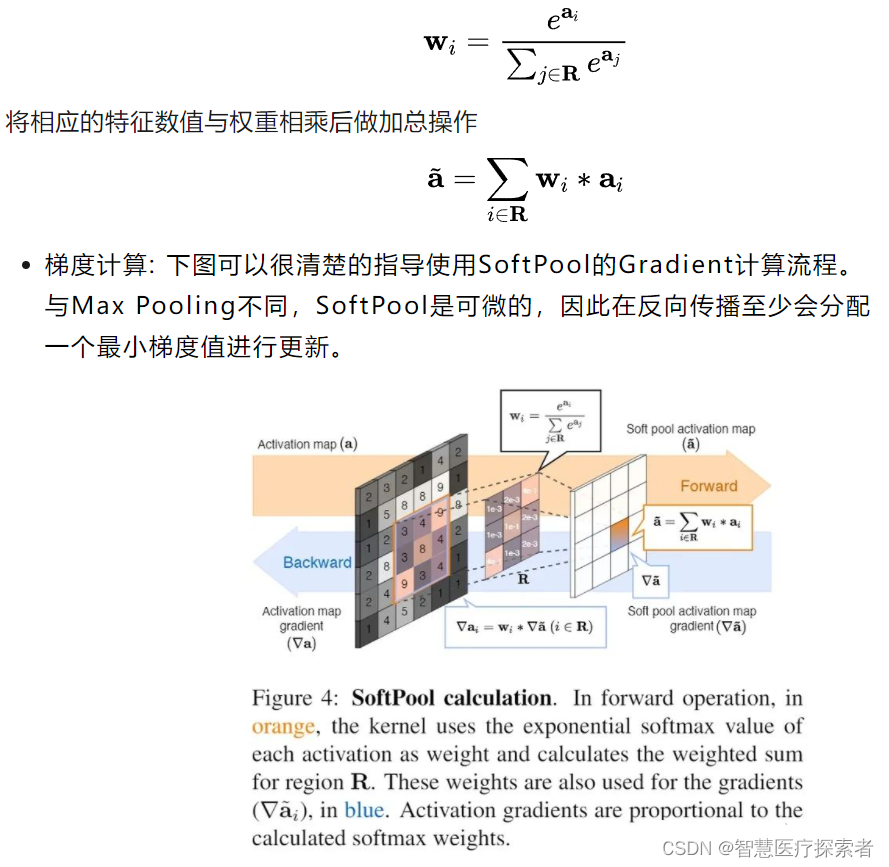
深度学习中的池化
1 深度学习池化概述 1.1 什么是池化 池化层是卷积神经网络中常用的一个组件,池化层经常用在卷积层后边,通过池化来降低卷积层输出的特征向量,避免出现过拟合的情况。池化的基本思想就是对不同位置的特征进行聚合统计。池化层主要是模仿人的…...

Java面试整理-Java设计模式
Java中的设计模式通常是从更广泛的面向对象设计模式中借鉴而来的,这些模式旨在解决特定的设计问题和改善代码的可维护性、灵活性和可扩展性。设计模式大致可以分为三类:创建型、结构型和行为型。以下是这三类中一些常见的设计模式: 创建型模式 单例模式(Singleton):确保一…...

用CHAT了解更多知识点
问CHAT:什么是硅基生命和碳基生命? CHAT回复:硅基生命和碳基生命是两种理论性的生物体类型,这些生物体主要是由硅或碳元素以及其他元素构成的。 碳基生命是我们当前所熟知的生命形式。碳元素能够形成稳定且复杂的分子,…...
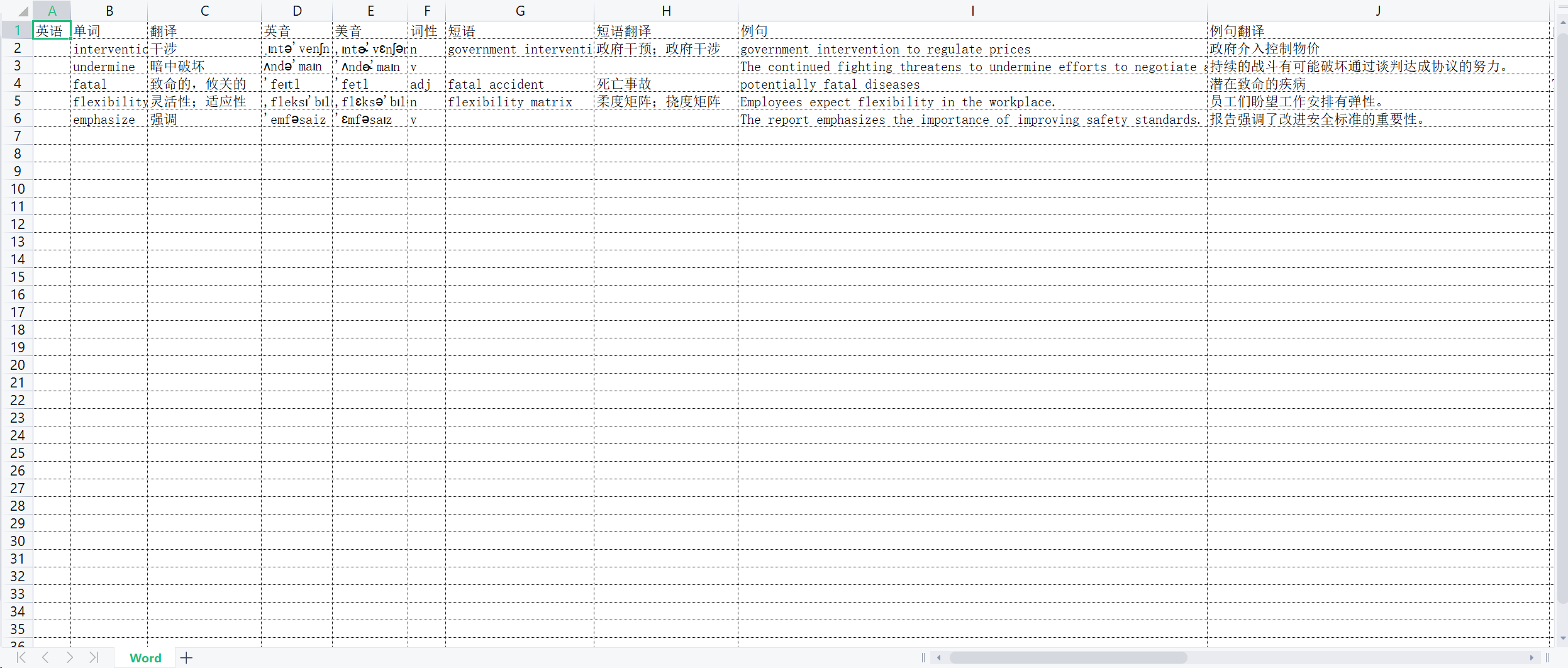
一个利用摸鱼时间背单词的软件
大家好,我是 Java陈序员。 最近进入了考试季,各种考试,英语四六级、考研、期末考等。不知道大家的英语四六级成绩怎么样呢? 记得大学时,英语四级都是靠高中学习积累的老本才勉强过关。 而六级则是考了多次ÿ…...
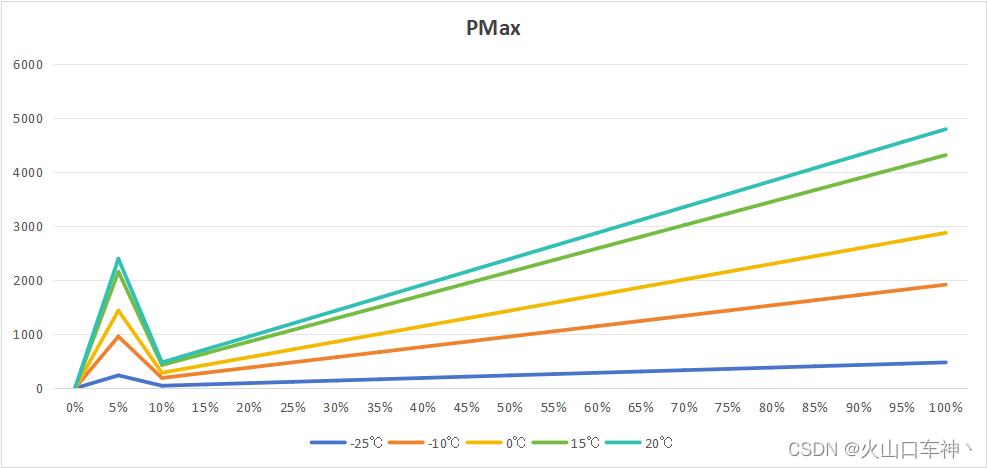
Matlab/Simulink的一些功能用法笔记(3)
01--引言 最近加入到一个项目组,有一些测试需要去支持,通过了解原先团队的测试方法后,自己作了如下改善,大大提高了工作效率。这也许就是软件开发的意义吧,能够去除一些重复的机械的人工操作并且结果还非常不可靠。 …...

Wafer晶圆封装工艺介绍
芯片封装的目的(The purpose of chip packaging): 芯片上的IC管芯被切割以进行管芯间连接,通过引线键合连接外部引脚,然后进行成型,以保护电子封装器件免受环境污染(水分、温度、污染物等)&…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

嵌入式学习之系统编程(九)OSI模型、TCP/IP模型、UDP协议网络相关编程(6.3)
目录 一、网络编程--OSI模型 二、网络编程--TCP/IP模型 三、网络接口 四、UDP网络相关编程及主要函数 编辑编辑 UDP的特征 socke函数 bind函数 recvfrom函数(接收函数) sendto函数(发送函数) 五、网络编程之 UDP 用…...

