【Leetcode Sheet】Weekly Practice 21
Leetcode Test
1901 寻找峰值Ⅱ(12.19)
一个 2D 网格中的 峰值 是指那些 严格大于 其相邻格子(上、下、左、右)的元素。
给你一个 从 0 开始编号 的 m x n 矩阵 mat ,其中任意两个相邻格子的值都 不相同 。找出 任意一个 峰值 mat[i][j] 并 返回其位置 [i,j] 。
你可以假设整个矩阵周边环绕着一圈值为 -1 的格子。
要求必须写出时间复杂度为 O(m log(n)) 或 O(n log(m)) 的算法
提示:
m == mat.lengthn == mat[i].length1 <= m, n <= 5001 <= mat[i][j] <= 105- 任意两个相邻元素均不相等.
【二分】
只考虑每一行的最大值,判断第i行的最大元素mat(i,j)
如果mat(i,j)大于上一行的元素mat(i-1,j)和下一行的元素mat(i+1,j),则符合题目的条件
/*** Note: The returned array must be malloced, assume caller calls free().*///找第i行的最大值
int Max(int *row,int n){int id=0;for(int i=0;i<n;i++){if(row[id]<row[i]){id=i;}}return id;
}int* findPeakGrid(int** mat, int matSize, int* matColSize, int* returnSize) {int m=matSize,n=matColSize[0];int low=0,high=m-1;//二分起始是第0行和第m-1行while(low<=high){int i=(low+high)/2;int j=Max(mat[i],n);if(i>=1 && mat[i][j]<mat[i-1][j]){//如果当前行 小于 上一行,说明峰值在上面,更新highhigh=i-1;continue;}if(i<m-1 && mat[i][j]<mat[i+1][j]){//如果当前行 小于 下一行,说明峰值在下面,更新lowlow=i+1;continue;}int *ret=malloc(sizeof(int)*2);ret[0]=i;ret[1]=j;*returnSize=2;return ret;}*returnSize=0;return NULL;
}
2828 判别首字母缩略词(12.20)
给你一个字符串数组 words 和一个字符串 s ,请你判断 s 是不是 words 的 首字母缩略词 。
如果可以按顺序串联 words 中每个字符串的第一个字符形成字符串 s ,则认为 s 是 words 的首字母缩略词。例如,"ab" 可以由 ["apple", "banana"] 形成,但是无法从 ["bear", "aardvark"] 形成。
如果 s 是 words 的首字母缩略词,返回 true ;否则,返回 false 。
提示:
1 <= words.length <= 1001 <= words[i].length <= 101 <= s.length <= 100words[i]和s由小写英文字母组成
【模拟】
bool isAcronym(char ** words, int wordsSize, char * s){int n=wordsSize,sn=strlen(s);if(n!=sn){return 0;}bool flag=1;for(int i=0;i<n;i++){if(s[i]!=words[i][0]){flag=0;break;}}return flag;
}
2866 美丽塔Ⅱ(12.21)
给你一个长度为 n 下标从 0 开始的整数数组 maxHeights 。
你的任务是在坐标轴上建 n 座塔。第 i 座塔的下标为 i ,高度为 heights[i] 。
如果以下条件满足,我们称这些塔是 美丽 的:
1 <= heights[i] <= maxHeights[i]heights是一个 山脉 数组。
如果存在下标 i 满足以下条件,那么我们称数组 heights 是一个 山脉 数组:
- 对于所有
0 < j <= i,都有heights[j - 1] <= heights[j] - 对于所有
i <= k < n - 1,都有heights[k + 1] <= heights[k]
请你返回满足 美丽塔 要求的方案中,高度和的最大值 。
提示:
1 <= n == maxHeights <= 1051 <= maxHeights[i] <= 109
【单调栈】
2866. 美丽塔 II - 力扣(LeetCode)
long long maximumSumOfHeights(int* maxHeights, int maxHeightsSize) {int n = maxHeightsSize;long long res = 0;long long prefix[n], suffix[n];int stack1[n], stack2[n];int top1 = 0, top2 = 0;for (int i = 0; i < n; i++) {while (top1 > 0 && maxHeights[i] < maxHeights[stack1[top1 - 1]]) {top1--;}if (top1 == 0) {prefix[i] = (long long)(i + 1) * maxHeights[i];} else {prefix[i] = prefix[stack1[top1 - 1]] + (long long)(i - stack1[top1 - 1]) * maxHeights[i];}stack1[top1++] = i;}for (int i = n - 1; i >= 0; i--) {while (top2 > 0 && maxHeights[i] < maxHeights[stack2[top2 - 1]]) {top2--;}if (top2 == 0) {suffix[i] = (long long)(n - i) * maxHeights[i];} else {suffix[i] = suffix[stack2[top2 - 1]] + (long long)(stack2[top2 - 1] - i) * maxHeights[i];}stack2[top2++] = i;res = fmax(res, prefix[i] + suffix[i] - maxHeights[i]);}return res;
}
左侧单调栈解析:maxHeights = [6, 5, 3, 9, 2, 7]
初始状态
maxHeights = [6, 5, 3, 9, 2, 7]stack1 = [](空栈)prefix = [0, 0, 0, 0, 0, 0]
步骤 1: i = 0 (maxHeights[0] = 6)
- 栈空,直接入栈。
prefix[0] = (0 + 1) * 6 = 6stack1 = [0]prefix = [6, 0, 0, 0, 0, 0]
步骤 2: i = 1 (maxHeights[1] = 5)
maxHeights[1]小于maxHeights[stack1[top1 - 1]](即maxHeights[0]), 弹出栈顶元素,栈变为空。prefix[1] = (1 + 1) * 5 = 10(因为栈为空)stack1 = [1]prefix = [6, 10, 0, 0, 0, 0]
步骤 3: i = 2 (maxHeights[2] = 3)
- 同样,
maxHeights[2]小于maxHeights[stack1[top1 - 1]](即maxHeights[1]), 弹出栈顶元素,栈变为空。 prefix[2] = (2 + 1) * 3 = 9(因为栈为空)stack1 = [2]prefix = [6, 10, 9, 0, 0, 0]
步骤 4: i = 3 (maxHeights[3] = 9)
maxHeights[3]大于maxHeights[stack1[top1 - 1]](即maxHeights[2]), 所以直接入栈。prefix[3] = prefix[stack1[top1 - 1]] + (3 - stack1[top1 - 1]) * maxHeights[3] = 9 + (3 - 2) * 9 = 18stack1 = [2, 3]prefix = [6, 10, 9, 18, 0, 0]
步骤 5: i = 4 (maxHeights[4] = 2)
maxHeights[4]小于maxHeights[stack1[top1 - 1]](即maxHeights[3]), 弹出栈顶元素。重复此过程,直到栈为空。prefix[4] = (4 + 1) * 2 = 10(因为栈为空)stack1 = [4]prefix = [6, 10, 9, 18, 10, 0]
步骤 6: i = 5 (maxHeights[5] = 7)
maxHeights[5]大于maxHeights[stack1[top1 - 1]](即maxHeights[4]), 所以直接入栈。prefix[5] = prefix[stack1[top1 - 1]] + (5 - stack1[top1 - 1]) * maxHeights[5] = 10 + (5 - 4) * 7 = 17stack1 = [4, 5]prefix = [6, 10, 9, 18, 10, 17]
1671 得到山形数组的最少删除次数(12.22)
我们定义 arr 是 山形数组 当且仅当它满足:
-
arr.length >= 3 -
存在某个下标
i(
从 0 开始
) 满足
0 < i < arr.length - 1且:
arr[0] < arr[1] < ... < arr[i - 1] < arr[i]arr[i] > arr[i + 1] > ... > arr[arr.length - 1]
给你整数数组 nums ,请你返回将 nums 变成 山形状数组 的 最少 删除次数。
提示:
3 <= nums.length <= 10001 <= nums[i] <= 109- 题目保证
nums删除一些元素后一定能得到山形数组。
【二分 + dp】
class Solution {
public:int minimumMountainRemovals(vector<int> &nums) {int n = nums.size();vector<int> suf(n), g;for (int i = n - 1; i; i--) {int x = nums[i];auto it = lower_bound(g.begin(), g.end(), x);suf[i] = it - g.begin() + 1; // 从 nums[i] 开始的最长严格递减子序列的长度if (it == g.end()) {g.push_back(x);} else {*it = x;}}int mx = 0;g.clear();for (int i = 0; i < n - 1; i++) {int x = nums[i];auto it = lower_bound(g.begin(), g.end(), x);int pre = it - g.begin() + 1; // 在 nums[i] 结束的最长严格递增子序列的长度if (it == g.end()) {g.push_back(x);} else {*it = x;}if (pre >= 2 && suf[i] >= 2) {mx = max(mx, pre + suf[i] - 1); // 减去重复的 nums[i]}}return n - mx;}
};
1962 移除石子使总数最小(12.23)
给你一个整数数组 piles ,数组 下标从 0 开始 ,其中 piles[i] 表示第 i 堆石子中的石子数量。另给你一个整数 k ,请你执行下述操作 恰好 k 次:
- 选出任一石子堆
piles[i],并从中 移除floor(piles[i] / 2)颗石子。
**注意:**你可以对 同一堆 石子多次执行此操作。
返回执行 k 次操作后,剩下石子的 最小 总数。
floor(x) 为 小于 或 等于 x 的 最大 整数。(即,对 x 向下取整)。
提示:
1 <= piles.length <= 1051 <= piles[i] <= 1041 <= k <= 105
【贪心 + 优先队列】
class Solution {
public:int minStoneSum(vector<int>& piles, int k) {priority_queue<int> pq(piles.begin(), piles.end());for (int i = 0; i < k; i++) {int pile = pq.top();pq.pop();pile -= pile / 2;pq.push(pile);}int sum = 0;while (!pq.empty()) {sum += pq.top();pq.pop();}return sum;}
};
【原地堆化】
class Solution {
public:int minStoneSum(vector<int> &piles, int k) {make_heap(piles.begin(), piles.end()); // 原地堆化(最大堆)while (k-- && piles[0] != 1) {pop_heap(piles.begin(), piles.end()); // 弹出堆顶并移到末尾piles.back() -= piles.back() / 2;push_heap(piles.begin(), piles.end()); // 把末尾元素入堆}return accumulate(piles.begin(), piles.end(), 0);}
};
1954 收集足够苹果的最小花园周长(12.24)
给你一个用无限二维网格表示的花园,每一个 整数坐标处都有一棵苹果树。整数坐标 (i, j) 处的苹果树有 |i| + |j| 个苹果。
你将会买下正中心坐标是 (0, 0) 的一块 正方形土地 ,且每条边都与两条坐标轴之一平行。
给你一个整数 neededApples ,请你返回土地的 最小周长 ,使得 至少 有 neededApples 个苹果在土地 里面或者边缘上。
|x| 的值定义为:
- 如果
x >= 0,那么值为x - 如果
x < 0,那么值为-x
提示:
1 <= neededApples <= 1015
【枚举】
long long minimumPerimeter(long long neededApples) {long long n=1;while(2*n*(n+1)*(2*n+1)<neededApples){n++;}return 4*(n*2);
}
【二分】
long long minimumPerimeter(long long neededApples) {long long left = 1, right = 100000, ans = 0;while (left <= right) {long long mid = (left + right) / 2;if (2 * mid * (mid + 1) * (mid * 2 + 1) >= neededApples) {ans = mid;right = mid - 1;} else {left = mid + 1;}}return ans * 8;
}
1276 不浪费原料的汉堡制作方案(12.25)
圣诞活动预热开始啦,汉堡店推出了全新的汉堡套餐。为了避免浪费原料,请你帮他们制定合适的制作计划。
给你两个整数 tomatoSlices 和 cheeseSlices,分别表示番茄片和奶酪片的数目。不同汉堡的原料搭配如下:
- **巨无霸汉堡:**4 片番茄和 1 片奶酪
- **小皇堡:**2 片番茄和 1 片奶酪
请你以 [total_jumbo, total_small]([巨无霸汉堡总数,小皇堡总数])的格式返回恰当的制作方案,使得剩下的番茄片 tomatoSlices 和奶酪片 cheeseSlices 的数量都是 0。
如果无法使剩下的番茄片 tomatoSlices 和奶酪片 cheeseSlices 的数量为 0,就请返回 []。
提示:
0 <= tomatoSlices <= 10^70 <= cheeseSlices <= 10^7
【数学:二元一次方程组】
/*** Note: The returned array must be malloced, assume caller calls free().*/
int* numOfBurgers(int tomatoSlices, int cheeseSlices, int* returnSize) {
if (tomatoSlices % 2 != 0 || tomatoSlices < cheeseSlices * 2 || cheeseSlices * 4 < tomatoSlices) {*returnSize = 0;return NULL;}int *ans = (int *)malloc(sizeof(int) * 2);ans[0] = tomatoSlices / 2 - cheeseSlices;ans[1] = cheeseSlices * 2 - tomatoSlices / 2;*returnSize = 2;return ans;
}/*
方程组
4x+2y=tomatoSlices
x+y=cheeseSlicesx= 1/2 tomatoSlices−cheeseSlices
y=2 cheeseSlices - 1/2 tomatoSlices
*/
相关文章:

【Leetcode Sheet】Weekly Practice 21
Leetcode Test 1901 寻找峰值Ⅱ(12.19) 一个 2D 网格中的 峰值 是指那些 严格大于 其相邻格子(上、下、左、右)的元素。 给你一个 从 0 开始编号 的 m x n 矩阵 mat ,其中任意两个相邻格子的值都 不相同 。找出 任意一个 峰值 mat[i][j] 并 返回其位置 [i,j] 。 …...

C语言使用qsort和bsearch实现二分查找
引言 在计算机科学领域,查找是一项基本操作,而二分查找是一种高效的查找算法。本博客将详细解释一个简单的C语言程序,演示如何使用标准库函数qsort和bsearch来对一个整数数组进行排序和二分查找。 代码解析 包含头文件 #include <stdi…...

MySQL的替换函数及补全函数的使用
前提: mysql的版本是8.0以下的。不支持树形结构递归查询的。但是,又想实现树形结构的一种思路 提示:如果使用的是MySQL8.0及其以上的,想要实现树形结构,请参考:MySQL数据库中,如何实现递归查询…...

2022第十二届PostgreSQL中国技术大会-核心PPT资料下载
一、峰会简介 本次大会以“突破•进化•共赢 —— 安全可靠,共建与机遇”为主题,助力中国数据库基础软件可掌控、可研究、可发展、可生产,并推动数据库生态的繁荣与发展。大会为数据库从业者、数据库相关企业、数据库行业及整个IT产业带来崭…...

2024 年 10大 AI 趋势
2025 年,全球人工智能市场预计将达到惊人的 1906.1 亿美元,年复合增长率高达 36.62%。 人工智能软件正在迅速改变我们的世界,而且这种趋势在未来几年只会加速。 我们分析了未来有望彻底改变 2024 年的 10 个AI趋势。从生成式人工智能的兴起到…...

Uboot
什么是Bootloader? Linux系统要启动就必须需要一个 bootloader程序,也就说芯片上电以后先运行一段bootloader程序。 这段 **bootloader程序会先初始化时钟,看门狗,中断,SDRAM,等外设,然后将 Linux内核从f…...

ECMAScript 的未来:预测 JavaScript 创新的下一个浪潮
以下是简单概括关于JavaScript知识点以及一些目前比较流行的比如:es6 想要系统学习: 大家有关于JavaScript知识点不知道可以去 🎉博客主页:阿猫的故乡 🎉系列专栏:JavaScript专题栏 🎉ajax专栏&…...

代码随想录算法训练营第十三天 | 239. 滑动窗口最大值、347.前 K 个高频元素
239. 滑动窗口最大值 题目链接:239. 滑动窗口最大值 给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。 返回 滑动窗口中的最大值 。 文章讲解…...

推荐五个免费的网络安全工具
导读: 在一个完美的世界里,信息安全从业人员有无限的安全预算去做排除故障和修复安全漏洞的工作。但是,正如你将要学到的那样,你不需要无限的预算取得到高质量的产品。这里有SearchSecurity.com网站专家Michael Cobb推荐的五个免费…...
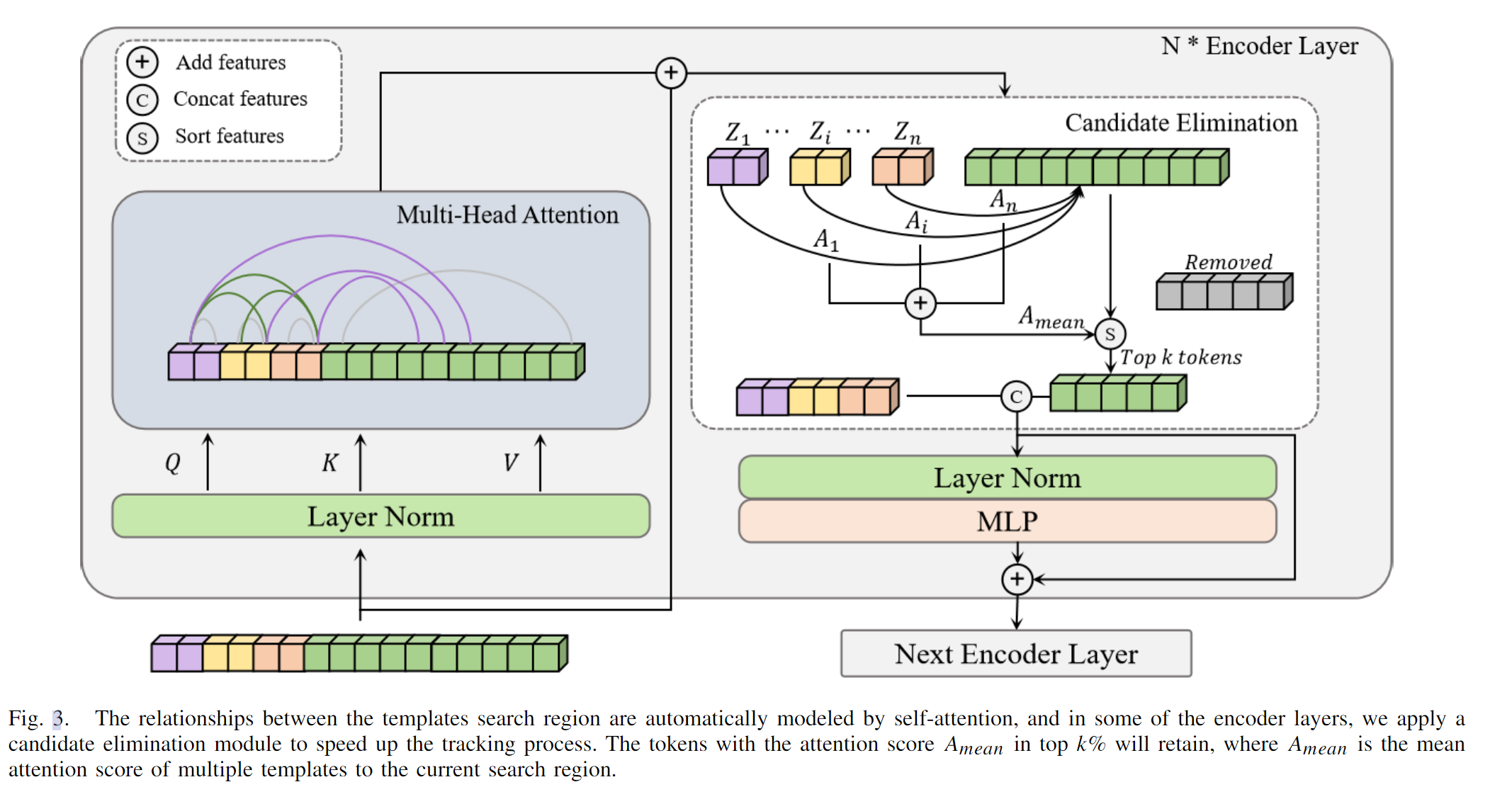
Cross-Drone Transformer Network for Robust Single Object Tracking论文阅读笔记
Cross-Drone Transformer Network for Robust Single Object Tracking论文阅读笔记 Abstract 无人机在各种应用中得到了广泛使用,例如航拍和军事安全,这得益于它们与固定摄像机相比的高机动性和广阔视野。多无人机追踪系统可以通过从不同视角收集互补的…...
【LeetCode刷题笔记】动态规划(二)
647. 回文子串 解题思路: 1. 暴力穷举 , i 遍历 [0, N) , j 遍历 [i+1, N] ,判断每一个子串 s[i, j) 是否是回文串,判断是否是回文串可以采用 对撞指针 的方法。如果是回文串就计数 +1...

(十七)Flask之大型项目目录结构示例【二扣蓝图】
大型项目目录结构: 问题引入: 在上篇文章讲蓝图的时候我给了一个demo项目,其中templates和static都各自只有一个,这就意味着所有app的模板和静态文件都放在了一起,如果项目比较大的话,这就非常乱…...

蓝牙技术在物联网中的应用
随着蓝牙技术的不断演进和发展,蓝牙已经从单一的传统蓝牙技术发展成集传统蓝牙。高速蓝牙和低耗能蓝牙于一体的综合技术,不同的应用标准更是超过40个越来越广的技术领域和越来越多的应用场景,使得目前的蓝牙技术成为包含传感器技术、识别技术…...
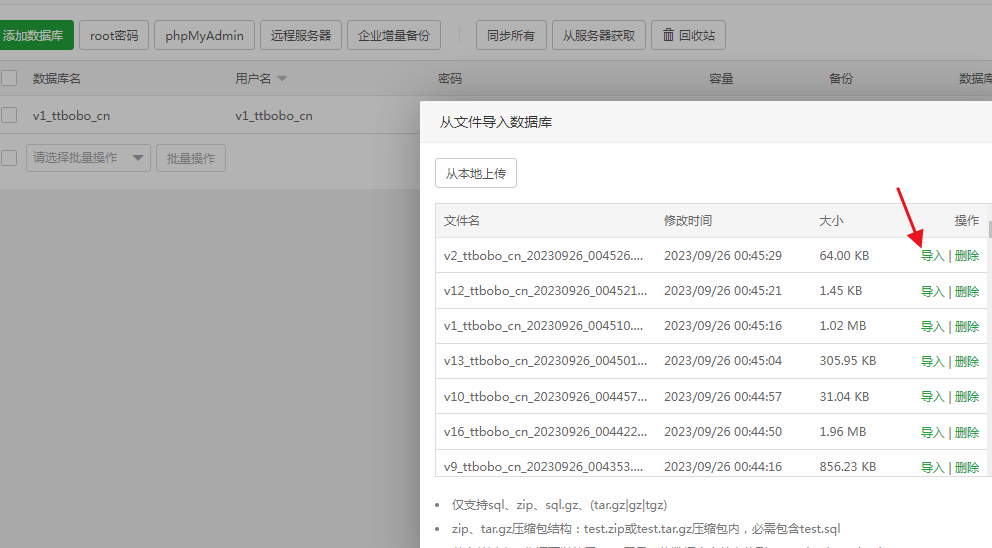
宝塔面板Linux服务器CentOS 7数据库mysql5.6升级至5.7版本教程
近段时间很多会员问系统更新较慢,也打算上几个好的系统,但几个系统系统只支持MYSQL5.7版本,服务器一直使用较低的MYSQL5.6版本,为了测试几个最新的系统打算让5.6和5.7并存使用,参考了多个文档感觉这种并存问题会很多。…...

掌握常用Docker命令,轻松管理容器化应用
Docker是一个开源的应用容器引擎,它可以让开发者将应用程序及其依赖打包到一个轻量级、可移植的容器中,然后发布到任何流行的Linux机器或Windows机器上,也可以实现虚拟化。容器是完全使用沙箱机制,相互之间不会有任何接口。下面介…...
(c++,multiset做法))
【数据结构1-2】P5076 普通二叉树(简化版)(c++,multiset做法)
文章目录 一、题目【深基16.例7】普通二叉树(简化版)题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1基本思路: 一、题目 【深基16.例7】普通二叉树(简化版) 题目描述 您需要写一种数据结构,来维…...

Linux系统安装及管理
目录 一、Linux应用程序基础 1.1应用程序与系统命令的关系 1.2典型应用程序的目录结构 1.3常见的软件包装类型 二、RPM软件包管理 1.RPM是什么? 2.RPM命令的格式 2,1查看已安装的软件包格式 2.2查看未安装的软件包 3.RPM安装包从哪里来? 4.挂…...
MySQL学生向笔记以及使用过程问题记录(内含8.0.34安装教程
MySQL 只会写代码 基本码农 要学好数据库,操作系统,数据结构与算法 不错的程序员 离散数学、数字电路、体系结构、编译原理。实战经验, 高级程序员 去IOE:去掉IBM的小型机、Oracle数据库、EMC存储设备,代之以自己在开源…...

obs video-io.c
video_frame_init 讲解 /* messy code alarm video_frame_init 函数用于初始化视频帧。它接受一个指向 struct video_frame 结构体的指针 frame, 视频格式 format,以及宽度 width 和高度 height。该函数根据视频格式的不同,计算出每个视频帧…...

简述 tcp 和 udp的区别?
简述 tcp 和 udp的区别? TCP(Transmission Control Protocol)和UDP(User Datagram Protocol)是两种不同的传输层协议,用于在计算机网络中进行数据传输。以下是它们的主要区别: 区别࿱…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...
