【C++、数据结构】位图、布隆过滤器、哈希切割(哈希思想的应用)
文章目录
- 📖 前言
- 1. 位图
- 1.1 海量数据处理思路分析:
- 1.2 位图的具体实现:
- 1.3 用位图解决问题:
- 应用一:
- 应用二:
- 应用三:
- 2. 布隆过滤器
- 2.1 布隆过滤器的概念:
- 2.2 布隆过滤器的测试:
- 2.3 布隆过滤器的删除:
- 2.4 布隆过滤器的应用:
- 3. 哈希切割(只提及思想)
📖 前言
之前我们学习了unordered_set和unordered_map的使用,并了解和模拟实现了其地层结构——哈希桶,并对自己实现的哈希桶进行了封装,封装模拟实现了的unordered_set和unordered_map,同时我们了解到,哈希表的查找性能很高时间复杂度为〇(1),所以其思想也得到了广泛的应用,本文我们就来介绍其思想的两个应用 —— 位图和布隆过滤器。
1. 位图
在STL官方库中也有位图:
位图使用文档介绍:

1.1 海量数据处理思路分析:
当我们有海量的数据要处理的时候,例如下面的例题:
【腾讯】 给40亿个不重复的无符号整数,没排过序。给一个无符号整数,如何快速判断一个数是否在
这40亿个数中。
- 首先我们先来大概的算一下,10亿个Byte(字节)大概是占几个G:
-
- 10亿Byte = 10亿 / 1024 KB = 10亿 / 1024 / 1024MB = 10亿 / 1024 / 1024 / 1024G = 0.93G
通过上面的计算我们得到,10亿个字节的数据大概是占1个G,那么40亿个无符号整数,则是占16个G的内存。
- 我们能否通过之前学的容器将这么多的数据存储进去:
- 很显然这更不可能,原因也很简单
-
- 以红黑树为例,每存4个Byte还要有4个Byte的消耗(颜色 + 三叉链)
-
- 哈希表也是类似的道理,但是比红黑树消耗小一点
- 我们能否通过排序的方式:
- 首先一点内排序肯定是不行的,数据量太大了
- 通过外排序 + 二分查找的方式(也是不可以的)
-
- 16G可以开出来,但是连续的16G就开不出来
-
- 文件不能随机读取,只能挨个挨个读取,所以是不支持二分查找的
-
- 同时外排序的话消耗也很大,这里的数据量也非常大
- 直接定址法哈希 —— 用一个比特位标识映射值在不在:
- 既然这么多数据我们存不了,我们的目的是判断其在不在这40亿个数据中
- 我们只需要标识一下该数字在不在就可以,这里采用用一个比特位标识
- 比特位是1就表示其在,比特位是0就表示其不在
-
- 那么我们知道无符号整数最大就是
4,294,967,295,我们只需要给0 ~ 4,294,967,295个比特位
- 那么我们知道无符号整数最大就是
-
- 就能将所有的无符号整数的范围都包含在内
-
- 接下来直接哈希映射,直接定址法映射
注意:
- 这里开的是42亿九千万个(整形最大值个)比特位,而不知题目中的40亿个
- 因为开的是范围,而不是个数
- 用一个比特位标识的原因
-
- 用一个比特位只能有两个值,正好表示两种状态
-
- 如果用一个
int来标识的话,那么一个int能标识256种状态
- 如果用一个
这就是用位图的方式来解决该问题。
1.2 位图的具体实现:
位图如何开空间:
因为我们开的是比特位的整数个,但是又没有直接精确控制到比特位个数的开空间方法,所以采用一下方式:

位图如何插入标识位:
这里的插入并不是直接将数据插入到位图中,而是将数据对应的哈希地址所在的比特位标识成1。

- 因为我们用的是
char为一个vector的数据类型,所以我们先定位在哪一个char中 - 例如:
18,我们先定位它在哪一个char中,所以我们18 / 8,先定好位 - 再用
18 % 8定位其具体在这个char中的哪一个比特位
如何实现插入?
我们想到了或运算和位运算:

只需要将1左移要标记的位之后与原来的数或一下,就成功标记好了。
如何实现删除:
- 同样的道理我们先定位到要删除的那个位置通过:
/、%操作 - 只需要将1左移要标记的位置之后,先取反,再与一下

如何实现查找:
- 只需要将1左移要标记的位置之后,直接与所在的char所表示的整数值与一下即可
通过任务管理器来查看内存

由图也就验证了开了四十二亿个比特位,大概是五百多MB。
具体代码:
//位图既节省空间又快。〇(1)就能判断
//N个比特位的位图 10 16
template<size_t N>//非类型模板参数
class bitset
{
public:bitset(){//+1保证足够比特位,最多浪费8个_bits.resize(N / 8 + 1, 0);}//x映射的位标记成1void set(size_t x){//x映射的比特位在第几个char对象size_t i = x / 8;//x在char第几个比特位size_t j = x % 8;_bits[i] |= (1 << j);}void reset(size_t x){//x映射的比特位在第几个char对象size_t i = x / 8;//x在char第几个比特位size_t j = x % 8;//! && ||//~ & | _bits[i] &= (~(1 << j));//不管原来的位置是1还是0,都要搞成0}//判断x在不在,是1返回true,是0返回falsebool test(size_t x){//x映射的比特位在第几个char对象size_t i = x / 8;//x在char第几个比特位size_t j = x % 8;return _bits[i] & (1 << j);}private:std::vector<char> _bits;//vector<int> _bits;
};
位图的应用
- 快速查找某个数据是否在一个集合中
- 排序 + 去重
- 求两个集合的交集、并集等
- 操作系统中磁盘块标记
1.3 用位图解决问题:
应用一:
1. 给定100亿个整数,设计算法找到只出现一次的整数。
- 我们知道无符号整数最多也就四十多亿个,100亿个必然有大量重复的。
- 我们来计算一下100亿个整数是多大,100亿个整数就是400亿个字节,那么大概就是40G的大小。
很显然用之前学的容器内存是放不下40G这么大的数据的,那我们如何用位图来解决?
- 先来分析一下,该用几个为来标识
- 分类一下:出现0次,出现1次,出现两次及以上的
- 那我们此时就要用两个比特位来标识
- 那我们是对之前的位图进行修改吗,这里我们并没有,而是直接复用两个位图
每个位图还是原来的大小(四十二亿九千万个),因为计算机表示的整数也就4,294,967,295个,其余的也都是重复。
- 我们知道100亿个整数的范围肯定是在
0 ~ 4,294,967,295之间的,所以我们开两个位图,重复的数对应的位置在每个表中是一样的。

- 此时我们就需要标识:00(一次都没出现的),01(只出现一次的),其他(出现两次及以上的)
template<size_t N>
class two_bitset
{
public:void set(size_t x){int in1 = _bs1.test(x);int in2 = _bs2.test(x);if (in1 == 0 && in2 == 0){_bs2.set(x);}else if (in1 == 0 && in2 == 1){_bs1.set(x);_bs2.reset(x);}}bool is_once(size_t x){return _bs1.test(x) == 0 && _bs2.test(x) == 1;}private://开两个位图复用前面操作bitset<N> _bs1;bitset<N> _bs2;
};
应用二:
2. 给两个文件,分别有100亿个整数,我们只有1G内存,如何找到两个文件交集?
因为只给了1个G的内存,我们首先想到的是用到两个位图,正好1个G。
解决办法:
- 在找交集之前我们一定要先做的是去重,对每个文件都要去重,不然就会找到重复交集。
-
- 方法一:分别将两个文件映射到两个位图中,挨个挨个比,利用对应算法找两个去重之后位图的交集
-
- 方法二:分别将两个文件映射到两个位图中,直接将两个位图与一下,剩下的就是交集了
应用三:
3. 位图应用变形:1个文件有100亿个int,1G内存,设计算法找到出现次数不超过2次的所有整数。
- 这题和应用一是一样的,只是多记录和判断了一次,因为不超过2次有:0、1、2。
- 分类一下:出现0次,出现1次,出现2次,出现两次以上的
- 同样是复用了两个位图

2. 布隆过滤器
在之前我们讲到了位图,他能迅速判断一个数是否在海量数据中。位图是直接映射,也不存在哈希冲突,空间消耗几乎没有,并且快,直接是O(1),但是位图只是适合于整形的查找,并不适用于浮点数字符串甚至是一些自定义类型的查找。
2.1 布隆过滤器的概念:
布隆过滤器是由 ==布隆(Burton Howard Bloom)==在1970年提出的一种紧凑型的、比较巧妙的概率型数据结构,特点是高效地插入和查询,可以用来告诉你 “某样东西一定不存在或者可能存在”,它是用个哈希函数,将一个数据映射到位图结构中。此种方式不仅可以提升查询效率,也可以节省大量的内存空间。
比如说是10亿个字符串是否在一个文件中。
我们来判断一下能否用红黑树哈希表来存储这10亿个字符串呢?
- 这肯定是不能的,因为10个Byte就是1G
- 假设每个字符串是10个Byte,那么光这么多字符串就已经占了十几个G了
- 还有红黑树和哈希表自带的消耗,那几十个G就没了,所以肯定不行
此时一个叫布隆的人,正如概念中所提到的运用了位图的思想,将字符串转化成一个整数,然后映射到位图当中。
如图我们给出一组ip:

- 我们运用哈希表中学的将字符串转成整数,在将转化成的整数映射到位图中。
- 但是布隆过滤器是无法解决哈希冲突的
-
- 首先映射到的是位图中,那么挂桶肯定是不行的,比特位挂不住桶
-
- 其次线性探测 / 二次探测也是不行的,因为在哈希表中可以对比数据,但是在位图中比不了,因为每个比特位仅仅是个标识位,并不是能比较
-
- 在:有可能是重复了的之前映射过了,又来了一个同样的字符串判段其在,或者是其他字符串通过哈希函数的转换之后,映射到了之前标记在的地方,造成了误判
-
- 不在:之前没有对应的字符串映射到为图中对应的位置,判断不在是准确的
-
- 所以字符串转整形必然会出现哈希冲突(因为字符串无限多),并且是解决不了的。
既然哈希冲突解决不了,那么我们就降低冲突的概率,降低误判:
布隆过滤器采用的是一个字符串映射多个值,在判断在不在时,当着多个值都存在的时候,才能判断其存在,不然就是不在。

- 有人就专门研究并统计了,误判率影响的因素
- 👉 误判率影响的因素研究统计报告
我们截取一下公式:

通过上述公式,我们哈希函数个数k取3得到:
也就是说在3个哈希函数的时候,没插入一个元素,就需要5个比特位来标识。
布隆过滤器是复用位图的:
struct BKDRHash
{size_t operator()(const string& s){//BKDRsize_t value = 0;for (auto ch : s){value *= 31;value += ch;}return value;}
};struct APHash
{size_t operator()(const string& s){size_t hash = 0;for (long i = 0; i < s.size(); i++){if ((i & 1) == 0){hash ^= ((hash << 7) ^ s[i] ^ (hash >> 3));}else{hash ^= (~((hash << 11) ^ s[i] ^ (hash >> 5)));}}return hash;}
};struct DJBHash
{size_t operator()(const string& s){size_t hash = 5381;for (auto ch : s){hash += (hash << 5) + ch;}return hash;}
};struct JSHash
{size_t operator()(const string& s){size_t hash = 1315423911;for (auto ch : s){hash ^= ((hash << 5) + ch + (hash >> 2));}return hash;}
};template<size_t M,class K = string,class HashFunc1 = BKDRHash,class HashFunc2 = APHash,class HashFunc3 = DJBHash,class HashFunc4 = JSHash>
class BloomFilter
{
public:void Set(const K& key){size_t hash1 = HashFunc1()(key) % M;size_t hash2 = HashFunc2()(key) % M;size_t hash3 = HashFunc3()(key) % M;size_t hash4 = HashFunc4()(key) % M;//cout << hash1 << " " << hash2 << " " << hash3 << endl;_bs.set(hash1);_bs.set(hash2);_bs.set(hash3);_bs.set(hash4);}bool Test(const K& key){size_t hash1 = HashFunc1()(key) % M;if (_bs.test(hash1) == false){return false;}size_t hash2 = HashFunc2()(key) % M;if (_bs.test(hash2) == false){return false;}size_t hash3 = HashFunc3()(key) % M;if (_bs.test(hash3) == false){return false;}size_t hash4 = HashFunc4()(key) % M;if (_bs.test(hash4) == false){return false;}return true; //存在误判}//布隆过滤器的删除可能会影响别的数据存储情况,所以不支持直接删除 -- 需要付出代价的bool Reset(const K& key);private:bitset<M> _bs;
};
2.2 布隆过滤器的测试:
测试1
void TestBloomFilter1()
{//插入10个值//BloomFilter<60, string, BKDRHash, APHash, DJBHash> bf;BloomFilter<60> bf;string a[] = { "苹果", "香蕉", "西瓜", "111111111", "eeeeeffff", "草莓", "休息", "继续", "查找", "set" };for (auto& e : a){bf.Set(e);}for (auto& e : a){cout << bf.Test(e) << " ";}cout << endl;cout << bf.Test("芒果") << " ";cout << bf.Test("string") << " ";cout << bf.Test("ffffeeeee") << " ";cout << bf.Test("31341231") << " ";cout << bf.Test("ddddd") << " ";cout << bf.Test("3333343") << " ";
}
我们提供了四个哈希函数,那么每插入一个数据就差不多需要60个比特位。

测试2:
void TestBloomFilter2()
{srand(time(0));const size_t N = 1000;//<>内放的是常量BloomFilter<6 * N> bf;std::vector<std::string> v1;std::string url = "https://www.cnblogs.com/-clq/archive/2012/05/31/2528153.html";for (size_t i = 0; i < N; i++){v1.push_back(url + std::to_string(1234 + i));}for (auto& str : v1){bf.Set(str);}std::vector<std::string> v2;for (size_t i = 0; i < N; ++i){std::string url = "https://www.cnblogs.com/-clq/archive/2012/05/31/2528153.html";url += std::to_string(999999 + i);v2.push_back(url);}size_t n2 = 0;for (auto& str : v2){if (bf.Test(str)){n2++;}}cout << "相似字符串误判率:" << (double)n2 / (double)N << endl;std::vector<std::string> v3;for (size_t i = 0; i < N; ++i){string url = "zhihu.com";url += std::to_string(rand());v3.push_back(url);}size_t n3 = 0;for (auto& str : v3){if (bf.Test(str)){n3++;}}cout << "不相似字符串误判率:" << (double)n3 / (double)N << endl;
}
我们分别对相似字符串和不相似字符串的误判率进行测试:

测试可见:布隆过滤器开的越大,误判率就越低。
2.3 布隆过滤器的删除:
因为布隆过滤器采用的是多组映射的方式,所以要是直接删除的话可能会影响其他的值存不存在的标识,所以布隆过滤器的删除是不能直接删除的。
布隆过滤器可以删除,但是要付出代价:
- 通过计数删除,映射一个值就在位图的标记位上计数
- 用到该位置就++,显然标识位不能再用比特位了
-
- 1bit标识一个位置
-
- 8bit标识一个位置 0 ~ 255
-
- 16bit标识一个位置 0 ~ 65535
- 还有溢出的风险
一个数删除之后,判断还在,说明是误判了。
此种方法的缺陷:
1.无法确认元素是否真正在布隆过滤器中
2.存在计数回绕
布隆过滤器优点:
1.增加和查询元素的时间复杂度为:O(K), (K为哈希函数的个数,一般比较小),与数据量大小无关
2.哈希函数相互之间没有关系,方便硬件并行运算
3.布隆过滤器不需要存储元素本身,在某些对保密要求比较严格的场合有很大优势
4.在能够承受一定的误判时,布隆过滤器比其他数据结构有这很大的空间优势
5.数据量很大时,布隆过滤器可以表示全集,其他数据结构不能
6.使用同一组散列函数的布隆过滤器可以进行交、并、差运算
布隆过滤器缺陷:
1.有误判率,即存在假阳性(False Position),即不能准确判断元素是否在集合中(补救方法:再建立一个白名单,存储可能会误判的数据)
2.不能获取元素本身
3.一般情况下不能从布隆过滤器中删除元素
4.如果采用计数方式删除,可能会存在计数回绕问题
2.4 布隆过滤器的应用:
1.注册的时候,快速判断一个昵称是否使用过:
- 将系统所有的昵称都映射到布隆过滤器中
- 不在:说明没人有用过
- 在:再去数据库查确认一遍(因为在的话存在误判)
2.黑名单:
- 不在:通行
- 在:再次去系统确认(绝不放过一个坏人,但有可能误抓好人)
3.过滤层,提高查找数据效率:

3. 哈希切割(只提及思想)
哈希切割:
- 给一个超过100G大小的log file, log中存着IP地址, 设计算法找到出现次数最多的IP地址?
- 与上题条件相同,如何找到top K的IP?
问题:
- 位图和布隆是Key的模型,无法解决Key_ Value的模型
- 只能哈希表和红黑树,但是内存又不够
解决方案一:
- 如何统计次数,很显然
100G的log中的IP肯定是不能放在红黑树或者哈希表中的。 - 这里我们采用将文件分割,假设将每个文件分成100份,每个文件就是1G就可以放在红黑树或者哈希表中了。
- 不过这里是存在问题的
-
- 会存在大量相同的IP会被分到不同的文件当中
-
- 如果要想统计个数,那么最后要合并还是会存在放不下的问题
解决方案二:
- 综合方案一的问题,我们就要将相同的IP放在同一个文件当中

然后再用红黑树和哈希表来统计:
 👉 TopK复习: 传送门
👉 TopK复习: 传送门
注意:
- 不同的ip也有可能进入同一个文件,但是相同的ip一定是进入同一个文件。
存在问题:
-
某个文件太大了,哈希表和红黑树中放不下
-
- a. 某个相同的ip太多 - 这时候存储大概率是够的,因为相同的ip存在map中只是统计次数,不额外占用空间。
-
- b. 映射冲突到这个编号文件的ip太多 - 但是冲突的太多的话,还是会大量文件存在小文件中,依旧会存在一个小文件太大的情况。
-
- 解决办法:是针对小文件再分割,再用其他哈希函数,进行哈希分割,再切分成小文件。

- 大量相同时,都集中在一个小文件,再去切分是不起作用的,切分完之后还是在同一个文件里
- a不会抛异常(大量相同的ip) ,b会抛异常(大量冲突不同的ip)
布隆过滤器找交集:
给两个文件,分别有100亿个query,我们只有1G内存,如何找到两个文件交集?分别给出精确算法和近似算法。
假设每个query平均30byte,100亿query就是300G。
似算法:
- 将一个文件映射到布隆过滤器中,用另一个文件去找,利用布隆过滤器的快速性,不过可能存在误判的问题。
- 所以这叫不精确的,近似算法。
精确算法:
- 方法: 相同的小文件找交集,对应编号找交集

- 通过哈希分割,A、B文件中相同的数据肯定被分到了相同的小文件
- 对小文件找交集,那么就很容易了,用set就可以很快找到
相关文章:

【C++、数据结构】位图、布隆过滤器、哈希切割(哈希思想的应用)
文章目录📖 前言1. 位图1.1 海量数据处理思路分析:1.2 位图的具体实现:1.3 用位图解决问题:应用一:应用二:应用三:2. 布隆过滤器2.1 布隆过滤器的概念:2.2 布隆过滤器的测试…...
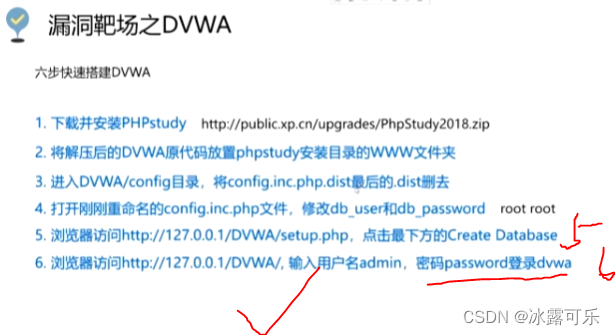
计算机网络安全基础知识3:网站漏洞,安装phpstudy,安装靶场漏洞DVWA,搭建一个网站
计算机网络安全基础知识3:网站漏洞,安装phpstudy,安装靶场漏洞DVWA,搭建一个网站 2022找工作是学历、能力和运气的超强结合体,遇到寒冬,大厂不招人,可能很多算法学生都得去找开发,测…...

大话数据结构-迪杰斯特拉算法(Dijkstra)和弗洛伊德算法(Floyd)
6 最短路径 最短路径,对于图来说,是两顶点之间经过的边数最少的路径;对于网来说,是指两顶点之间经过的边上权值之和最小的路径。路径上第一个顶点为源点,最后一个顶点是终点。 6.1 迪杰斯特拉(Dijkstra&am…...

2023年全国最新食品安全管理员精选真题及答案10
百分百题库提供食品安全管理员考试试题、食品安全员考试预测题、食品安全管理员考试真题、食品安全员证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 91.实施日常检查,如果违反关键项的,应当即作出如…...
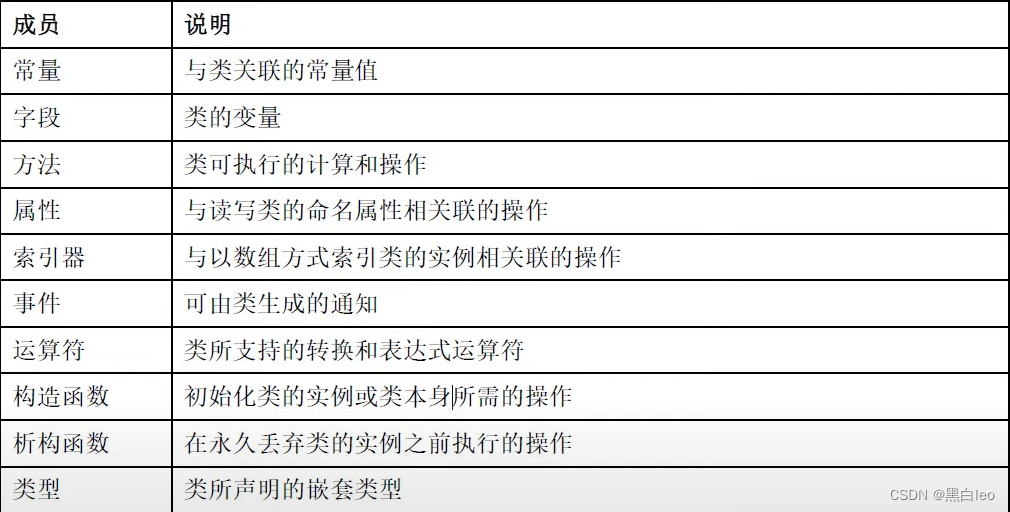
Unity常见面试题详解(持续更新...)
一丶声明、定义、实例化、初始化 1、首先我们来讨论在C/C中的声明和定义.. 1)我们先从函数声明和定义说起... 一般我们在C里都会先定义一个函数,然后再Main函数前将函数声明,比如: //函数声明 int Add(int);int Main {} //函数…...
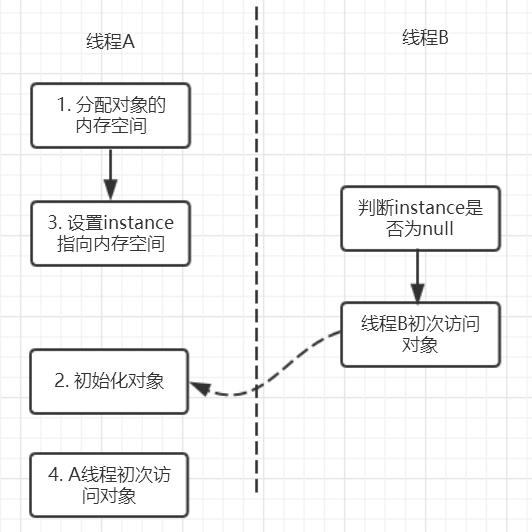
java高级篇之三大性质总结:原子性、可见性以及有序性
1. 三大性质简介 在并发编程中分析线程安全的问题时往往需要切入点,那就是两大核心:JMM抽象内存模型以及happens-before规则(在这篇文章中已经经过了),三条性质:原子性,有序性和可见性。关于sy…...
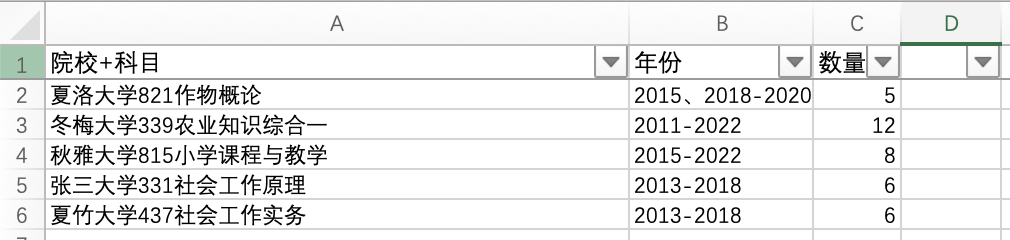
真涨脸,我用 Python 为朋友自动化整理表格
今天,在工作的时候,我的美女同事问我有没有办法自动生成一个这样的表格: 第一列是院校科目,第二列是年份,第三列是数量。 这张表格是基于这一文件夹填充的,之前要一个文件夹一个文件夹打开然后手动填写年份…...
MySQL学习笔记(1.操作数据库与数据的SQL)
1. 下载安装 参照:MySQL8.0下载安装_凯尔萨厮的博客-CSDN博客 2. MySQL启动与停止 方式(1).我的电脑>右键>管理>服务和应用程序>服务>(或在windows搜索栏输入services.msc) 找到MySQL80,右键启动或停止 方式(2…...

C++——特殊类设计
目录 不能被拷贝的类 只能在堆上创建对象的类 只能在栈上创建对象的类 不能被继承的类 只能创建一个对象的类(单例模式) 饿汉模式 懒汉模式 单例对象释放问题 不能被拷贝的类 C98:将拷贝构造函数与赋值运算符重载只声明不定义,并且将其访问权…...

Scratch少儿编程案例-植物大战僵尸-趣味角色版
专栏分享 点击跳转=>Unity3D特效百例点击跳转=>案例项目实战源码点击跳转=>游戏脚本-辅助自动化点击跳转=>Android控件全解手册点击跳转=>Scratch编程案例👉关于作者...

Vue的路由守卫
对于绝大部分的网站而言,都是有个人主页的,但是你如果没登陆的话,还能访问个人主页吗? 从逻辑上来讲,那肯定是不行的。 所以,要怎么阻止没登录状态下去访问个人主页呢? 就是利用路由守卫&#x…...

【算法】151. 反转字符串中的单词
链接:https://leetcode.cn/problems/reverse-words-in-a-string/给你一个字符串 s ,请你反转字符串中 单词 的顺序。单词 是由非空格字符组成的字符串。s 中使用至少一个空格将字符串中的 单词 分隔开。返回 单词 顺序颠倒且 单词 之间用单个空格连接的结…...
-认知服务(2))
Azure AI基础到实战(C#2022)-认知服务(2)
目录 ComputerVisionClient Class定义构造函数属性上一节例子Task.Wait 方法其它部分分析winform调用认知服务代码剖析1、调用参数2、定义ComputerVisionClient对象,准备调用 REST API3、Authenticate4、调用REST API,这是重点和关键(1)Lambda 表达式和匿名函数(2)async(3)…...

并发就一定快吗?答:肯定不是啊
文章目录一、多线程概念1.1 程序的并发与并行1.1.1 程序的并行1.1.2 程序的并发1.2 进程与线程1.2.1 进程1.2.2 线程1.2.3 多线程并发就一定快吗?答案直接戳这里👉:多线程并发就一定快吗? 一、多线程概念 在实际应用中ÿ…...

前端的学习路线和方法
一些前端工程师面临的现状 1.没有系统的的学习基础知识 2.技术上存在短板,说句不好听的话,大多数开发者的上升通道都没有明确的路线,大公司还好,小公司基本都是后端作为开发组组长 3.前端各种技术层出不穷,需要花费…...
用C语言写一个自己的shell-Part Ⅱ--execute commands
Part Ⅱ–execute commands Exec This brings us to the exec family of functions. Namely, it has the following functions: execlexecvexecleexecveexeclpexecvp For our needs,we will use execvp whose signature looks like this int execvp(const char *file, cha…...

案例实践|运营腾讯游戏,Proxima Beta 使用 Apache Pulsar 升级团队协作与数据治理...
文章摘要本文整理自 Pulsar Summit Asia 2022 上,Proxima Beta 软件工程师施磊的分享《How to achieve better team integration and data governance by using Apache Pulsar》。本文首先将为大家介绍 CQRS 和 Event Sourcing 概念,便于了解为何 Proxim…...
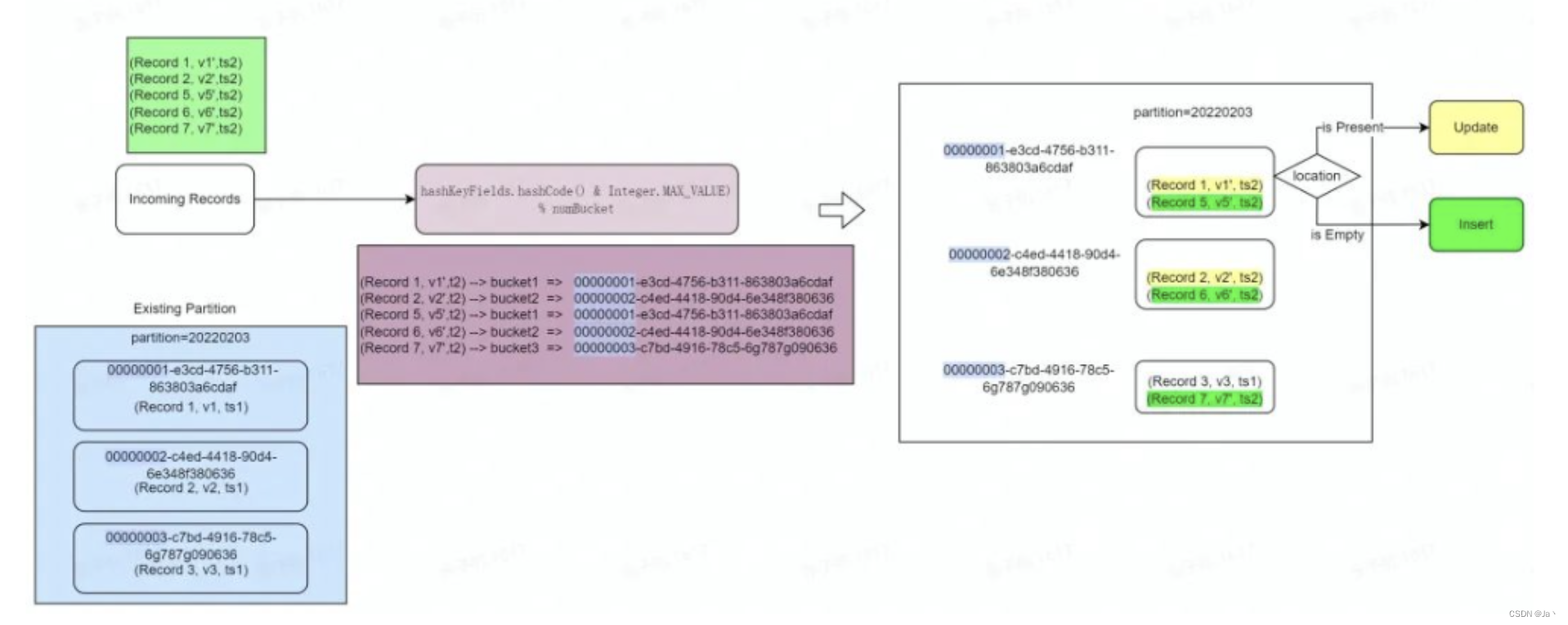
Hudi的7种索引
1、Bloom Index Bloom Index (default) 使用根据记录键构建的bloom过滤器,也可以使用记录键范围修剪候选文件.原理为计算RecordKey的hash值然后将其存储到bitmap中,为避免hash冲突一般选择计算3次 HoodieKey 主键信息:主要包含recordKey 和p…...
系统软中断 software)
Linux内核(十三)系统软中断 software
文章目录中断概述Linux内核中断软中断相关代码解析软中断结构体软中断类型软中断两种触发方式函数__do_softirq解析定时器的软中断实现解析定时器相关代码总结Linux版本:linux-3.18.24.x 中断概述 中断要求 快进快出,提高执行效率,…...
Linux -- 查看进程 PS 命令 详解
我们上篇介绍了, Linux 中的进程等概念,那么,在Linux 中如何查看进程呢 ??我们常用到的有两个命令, PS 和 top 两个命令,今天先来介绍下 PS 命令~!PS 命令 :作用 &#x…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...
