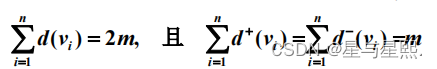第九部分 图论
目录
例
相关概念
握手定理
例1
图的度数列
例
无向图的连通性
无向图的连通度
例2
例3
有向图D如图所示,求 A, A2, A3, A4,并回答诸问题:
中间有几章这里没有写,感兴趣可以自己去学,组合数学跟高中差不多,这里也没写了,绝不是因为作者懒!
定义9 .1 无向图 G = < V , E >, 其中(1) V ≠ ∅ 为顶点集,元素称为 顶点(2) E 为 V & V 的多重集,其元素称为无向边,简称 边
例
G = <V,E>为无向图
V = { v 1, v2, v3,v4,v5}E = {( v 1 , v 1 ), ( v 1 , v 2 ), ( v 2 , v 3 ), ( v 2 , v 3 ), ( v 2 , v 5 ), ( v 1 , v 5 ), ( v 4 , v 5 )}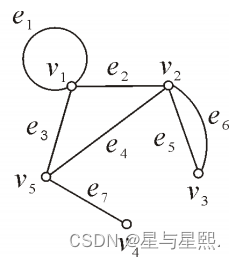
定义9 .2 有向图 D =< V , E >, 只需注意 E 是 V × V 的多重子集
相关概念
1. 图① 可用 G 泛指图(无向的或有向的)② V ( G ), E ( G ), V ( D ), E ( D )③ n 阶图2. 有限图3. n 阶零图与平凡图4. 空图 —— ∅5. 用 e k 表示无向边或有向边6. 顶点与边的关联关系① 关联、关联次数② 环③ 孤立点7. 顶点之间的相邻与邻接关系8. 邻域与关联集① v ∈ V ( G ) ( G 为无向图 )v的邻域 N(v)={u|u∈V(G)∧(u,v)∈E(G)∧u≠v}v的闭邻域(v)=N(v)∪{v}
v的关联集 I(v)={e|e∈E ( G ) ∧ e 与 v 关联 }② v ∈ V ( D ) ( D 为有向图 )v的后继元集(v)={u|u∈V(D) ∧<v,u>∈E(D) ∧u≠v}
v的先驱元集(v)= {u|u∈V(D) ∧<u,v>∈E(D) ∧u≠v}
v的邻域(v)=
(v)∪
(v)
v的闭邻域(v)=
(v)∪{v}
9. 标定图与非标定图10. 基图
定义9 .3(1) 无向图中的平行边及重数(2) 有向图中的平行边及重数 注意方向性(3) 多重图(4) 简单图
定义9 .4(1) 设 G =< V , E > 为无向图 , ∀ v ∈ V , d ( v )—— v 的度数 , 简称度(2) 设 D =< V , E > 为有向图∀ v ∈ Vd + ( v )—— v 的出度d − ( v )—— v 的入度d ( v )—— v 的度或度数(3)∆ ( G )最大度δ ( G )最小度(4)∆ + ( D )最大出度δ + ( D )最小出度∆ − ( D )最大入度δ − ( D )最小入度(5) 奇顶点度与偶度顶点
握手定理
定理9.1 设G=<V,E>为任意无向图,V={v1,v2,…,vn}, |E|=m, 则
G 中每条边 ( 包括环 ) 均有两个端点,所以在计算 G 中各顶点 度数之和时,每条边均提供 2 度, m 条边共提供 2 m 度
定理9.2 设D=<V,E>为任意有向图,V={v1,v2,…,vn}, |E|=m, 则
总度数为边数的两倍,入度和出度都等于边数
例1
无向图 G 有 16 条边, 3 个 4 度顶点, 4 个 3 度顶点,其余 顶点度数均小于 3 ,问 G 的阶数 n 为几?解本题的关键是应用握手定理设除 3 度与 4 度顶点外还有 x 个顶点 v 1 , v 2 , …, v x则d ( v i ) ≤ 2 , i =1, 2, …, x于是得不等式32 ≤ 24+2 x得 x ≥ 4阶数 n ≥ 4+4+3=11
图的度数列
V ={ v 1 , v 2 , …, v n } 为无向图 G 的顶点集,称 d ( v 1 ), d ( v 2 ), …, d ( v n ) 为 G 的 度数列V ={ v 1 , v 2 , …, v n } 为有向图 D 的顶点集D 的 度数列 : d ( v 1 ), d ( v 2 ), …, d ( v n )D 的 出度列 : d + ( v 1 ), d + ( v 2 ), …, d + ( v n )D 的 入度列 : d − ( v 1 ), d − ( v 2 ), …, d − ( v n )非负整数列 d =( d 1 , d 2 , …, d n ) 是 可图化的 ,是 可简单图化 的度数列=入度列+出度列,对应元素例
度数列={3,2,3,2}
出度列={2,1,2,1}
则求入读列
{1,1,1,1}
定义9 .5 设 G 1 =< V 1 , E 1 >, G 2 =< V 2 , E 2 > 为两个无向图 ( 两个有向 图 ) ,若存在双射函数 f : V 1 → V 2 , 对于 v i , v j ∈ V 1 , ( v i , v j ) ∈ E 1 当且仅当 ( f ( v i ), f ( v j )) ∈ E 2 ( < v i , v j > ∈ E 1 当且仅当 < f ( v i ), f ( v j )> ∈ E 2 ) 并且 , ( v i , v j ) ( < v i , v j > )与 ( f ( v i ), f ( v j )) ( < f ( v i ), f ( v j )> )的重数相 同,则称 G 1 与 G 2 是 同构 的,记作 G 1 ≅ G 2
图之间的同构关系具有自反性、对称性和传递性能找到多条同构的必要条件,但它们全不是充分条件:① 边数相同,顶点数相同② 度数列相同③ 对应顶点的关联集及邻域的元素个数相同 等若破坏必要条件,则两图不同构判断两个图同构是个难题
定义9.6
(1) n ( n ≥ 1) 阶无向完全图 —— 每个顶点与其余顶点均相邻的 无向简单图,记作 K n简单性质:边数m = n ( n − 1) /2∆ = δ = n − 1(2) n ( n ≥ 1) 阶 有向完全图 —— 每对顶点之间均有两条方向相 反的有向边的有向简单图简单性质:m = n ( n − 1)∆ = δ = 2( n − 1)∆ + = δ + = n − 1(3) n ( n ≥ 1) 阶 竞赛图 —— 基图为 K n 的有向简单图简单性质:边数m = n ( n 2 − 1)∆ = δ = n − 1
定义9.7 n 阶k正则图——∆=δ=k 的无向简单图
简单性质:边数(由握手定理得)
m=nk/2
定义9 .8 G =< V , E >, G ′ =< V ′ , E ′ >(1) G ′⊆ G —— G ′ 为 G 的 子图 , G 为 G ′ 的 母图(2) 若 G ′⊆ G 且 V ′ = V ,则称 G ′ 为 G 的 生成子图(3) 若 V ′⊂ V 或 E ′⊂ E ,称 G ′ 为 G 的 真子图(4) V ′ ( V ′⊂ V 且 V ′≠∅ )的 导出子图 ,记作 G [ V ′ ](5) E ′ ( E ′⊂ E 且 E ′≠∅ )的 导出子图 ,记作 G [ E ′ ]
定义9 .9 设 G =< V , E > 为 n 阶无向简单图,以 V 为顶点集,以 所有使 G 成为完全图 K n 的添加边组成的集合为边集的图, 称为 G 的 补图 ,记作 G若G≅ G , 则称G是自补图.
定义9 .10 给定图 G =< V , E > (无向或有向的), G 中 顶点与 边的交替序列 Γ = v 0 e 1 v 1 e 2 … e l v l , v i − 1 , v i 是 e i 的端点(1) 通路与回路: Γ 为 通路 ;若 v 0 = v l , Γ 为 回路 , l 为 回路长 度(2) 简单通路与回路:所有边各异, Γ 为 简单通路 ,又若 v 0 = v l , Γ 为 简单回路(3) 初级通路 ( 路径 ) 与初级回路 ( 圈 ) : Γ 中所有顶点各异,则 称 Γ 为 初级通路 ( 路径 ) ,又若除 v 0 = v l ,所有的顶点各不相 同且所有的边各异,则称 Γ 为 初级回路 ( 圈 )(4) 复杂通路与回路:有边重复出现
定理9 .3 在 n 阶图 G 中,若从顶点 v i 到 v j ( v i ≠ v j )存在通路, 则从 v i 到 v j 存在长度小于或等于 n − 1 的通路定理9 .4 在一个 n 阶图 G 中,若存在 v i 到自身的回路,则一 定存在 v i 到自身长度小于或等于 n 的回路
无向图的连通性
(1) 顶点之间的连通关系: G =< V , E > 为无向图① 若 v i 与 v j 之间有通路,则 v i ∼ v j② ∼ 是 V 上的等价关系 R ={< u , v >| u , v ∈ V 且 u ∼ v }(2) G 的连通性与连通分支① 若 ∀ u , v ∈ V , u ∼ v ,则称 G 连通② V / R ={ V 1 , V 2 ,…, V k } ,称 G [ V 1 ], G [ V 2 ], …, G [ V k ] 为 连通分 支 ,其个数 p ( G )= k ( k ≥ 1)k =1 , G 连通(3) 短程线与距离① u 与 v 之间的 短程线 : u ∼ v , u 与 v 之间长度最短的通路② u 与 v 之间的 距离 : d ( u , v )—— 短程线的长度③ d ( u , v ) 的性质:d ( u , v ) ≥ 0, u ≁ v 时 d ( u , v )= ∞d ( u , v )= d ( v , u )d ( u , v )+ d ( v , w ) ≥ d ( u , w )
无向图的连通度
删除顶点及删除边G − v —— 从 G 中将 v 及关联的边去掉G − V ′ —— 从 G 中删除 V ′ 中所有的顶点G − e —— 将 e 从 G 中去掉G − E ′ —— 删除 E ′ 中所有边点割集与边割集点割集与割点
定义9.11 G=<V,E>, V′⊂V
V ′ 为 点割集 —— p ( G − V ′ )> p ( G ) 且有极小性v 为 割点 ——{ v } 为点割集定义9 .12 G =< V , E >, E ′⊆ EE ′ 是 边割集 —— p ( G − E ′ )> p ( G ) 且有极小性e 是 割边 (桥) ——{ e } 为边割集
点割集和边割集的两个要求
删去集合里的所有边或点,会增加连通分支
删去集合中的子集不会增加连通分支
例2
点割集 {v5},{v6},{v1,v4}
割点 v5,v6
边割集 {e7},{e8},{e1,e2},{e1,e4,e6},{e2,e3,e9},{e1,e3,e9},{e2,e4,e6},{e3,e4,e5},{e1,e3,e5,e6},{e2,e4,e5,e9},{e1,e4,e5,e9},{e2,e3,e5,e9}
割边(桥) e7,e8
定义9 .13 D =< V , E > 为有向图v i → v j ( v i 可达 v j ) —— v i 到 v j 有通路v i ↔ v j ( v i 与 v j 相互可达)性质→ 具有自反性 ( v i → v i ) 、传递性↔ 具有自反性、对称性、传递性v i 到 v j 的短程线与距离类似于无向图中,只需注意距离表示法的不同( 无向图中 d ( v i , v j ) ,有向图中 d < v i , v j >) 及 d < v i , v j > 无对称性
定义9.14 D=<V,E>为有向图
D 弱连通 ( 连通 )—— 基图为无向连通图D 单向连通 —— ∀ v i , v j ∈ V , v i → v j 或 v j → v iD 强连通 —— ∀ v i , v j ∈ V , v i ↔ v j易知,强连通 ⇒ 单向连通 ⇒ 弱连通
判别法定理9 .4 D 强连通当且仅当 D 中存在经过每个顶点至少一次 的回路定理9 .5 D 单向连通当且仅当 D 中存在经过每个顶点至少一 次的通路
定义9.15 设 G =< V , E > 为一个无向图,若能将 V 分成 V 1 和 V 2 ( V 1 ∪ V 2 = V , V 1 ∩ V 2 = ∅ ) ,使得 G 中的每条边的两个端点都是 一个属于 V 1 ,另一个属于 V 2 ,则称 G 为 二部图 ( 或称 二分图 、 偶图 等 ) ,称 V 1 和 V 2 为 互补顶点子集 ,常将二部图 G 记为 < V 1 , V 2 , E > 又若 G 是简单二部图, V 1 中每个顶点均与 V 2 中所有的顶点相 邻 则称 G 为 完全二部图 ,记为 K r , s ,其中 r =| V 1 | , s =| V 2 |注意, n 阶零图为二部图完全二部图V1集合每个点都与V2集合中每个点相连
定理9.6 无向图G=<V,E>是二部图当且仅当G中无奇圈
定义9 .16 无向图 G =< V , E > , | V |= n , | E |= m ,令 m ij 为 v i 与 e j 的关联次数,称 ( m ij ) n × m 为 G 的 关联矩阵 ,记为 M ( G )
定义9 .17 有向图 D =< V , E > ,令 则称 ( m ij ) n × m 为 D 的 关联矩阵 ,记为 M ( D )
定义9 .18 设有向图 D =< V , E >, V ={ v 1 , v 2 , …, v n }, E ={ e 1 , e 2 , …, e m }, 令为顶点 v i 邻接到顶点 v j 边的条数,称为 D 的 邻接矩 阵 ,记作 A ( D ) ,或简记为 A
定理9.7 设 A为有向图 D 的邻接矩阵,V={v1, v2, …, vn}为顶点集,则 A 的 l 次幂 Al (l≥1)中元素
为D中vi 到vj 长度为 l 的通路数,其中
为vi 到自身长度为 l 的回路数,而
为D中长度为 l 的通路总数,
为D 中长度为 l 的回路总数
例3
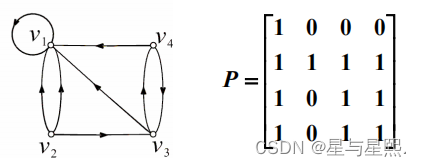
有向图D如图所示,求 A, A2, A3, A4,并回答诸问题:
(1) D 中长度为 1, 2, 3, 4 的通路各有多少条?其中回路分别为多 少条?(2) D 中长度小于或等于 4 的通路为多少条?其中有多少条回路?
(1)D 中长度为 1 的通路为 8 条,其中有 1 条是回路D 中长度为 2 的通路为 11 条,其中有 3 条是回路D 中长度为 3 和 4 的通路分别为 14 和 17 条,回路分别 为 1 与 3 条(2)D 中长度小于等于 4 的通路为 50 条,其中有 8 条是回路下标(i,i)的数的和为回路总数,(i,j)的数的和为通路总数
定义9.19 设D=<V,E>为有向图. V={v1, v2, …, vn}, 令
称 (pij)n×n 为D的可达矩阵,记作P(D),简记为由于∀vi ∈V,vi ↔vi ,所以P(D)主对角线上的元素全为1
由定义不难看出, D 强连通当且仅当P(D)为全1矩阵
下图所示有向图 D 的可达矩阵为
相关文章:
第九部分 图论
目录 例 相关概念 握手定理 例1 图的度数列 例 无向图的连通性 无向图的连通度 例2 例3 有向图D如图所示,求 A, A2, A3, A4,并回答诸问题: 中间有几章这里没有写,感兴趣可以自己去学,组合数学跟高中差不多,…...

如何用java实现对java虚拟机的性能监控?
要使用Java实现对Java虚拟机(JVM)的性能监控,可以使用Java Management Extensions(JMX)来获取和监控JVM的各种指标。以下是一个简单的示例代码,演示如何使用JMX监控JVM的内存使用情况: import …...
电路设计(7)——窗口比较器的multism仿真
1.功能设计 构建一个窗口比较器的电路,在输入电压大于3.5v,小于0.8v时,蜂鸣器报警,输入电压在0.8v到3.5v之间时,不报警。 整体电路如下: 2.设计思路 在输入端,采取电阻分压的方式,输…...

前端已死?探讨人工智能与低代码对前端的影响
文章目录 每日一句正能量前言前端行业究竟是好是坏?数字化转型的当下前端工程师该何去何从? 想要入行前端先认清这三个事实 后记 每日一句正能量 人的结构就是相互支撑,众人的事业需要每个人的参与。 前言 随着人工智能和低代码的崛起&#…...

树莓派,opencv,Picamera2利用舵机云台追踪人脸(PID控制)
一、需要准备的硬件 Raspiberry Pi 4b两个SG90 180度舵机(注意舵机的角度,最好是180度且带限位的,切勿选360度舵机)二自由度舵机云台(如下图)Raspiberry CSI 摄像头 组装后的效果: 二、项目目…...

uniapp中推出当前微信小程序
uni.exitMiniProgram() 通过代码直接退出当前小程序 uni.exitMiniProgram({success: function() {console.log(退出小程序成功);},fail: function(err) {console.log(退出小程序失败, err);} })...

AndroidStudio无法新建aidl文件解决办法
我用的 AS 版本是 Android Studio Giraffe | 2022.3.1 Build #AI-223.8836.35.2231.10406996, built on June 29, 2023 右键新建 aidl 文件, 提示 (AIDL File)Requires setting the buildFeatures.aidl to true in the build file 解决办法 修改 app 的 build.…...

java爬虫(jsoup)如何设置HTTP代理ip爬数据
目录 前言 什么是HTTP代理IP 使用Jsoup设置HTTP代理IP的步骤 1. 导入Jsoup依赖 2. 创建HttpProxy类 3. 设置代理服务器 4. 使用Jsoup进行爬取 结论 前言 在Java中使用Jsoup进行网络爬虫操作时,有时需要使用HTTP代理IP来爬取数据。本文将介绍如何使用Jsoup设…...

ZooKeeper Client API 安装及使用指北
下载 wget https://archive.apache.org/dist/zookeeper/zookeeper-3.5.4-beta/zookeeper-3.5.4-beta.tar.gz解压 tar -zxf zookeeper-3.5.4-beta.tar.gz安装 cd zookeeper-3.5.4-beta/src/c/ ./configure make sudo make install到 make 这一步大概率会出现报错:…...
本机ping不通虚拟机
windows下finall shell连不上虚拟机了,之前是可以的,然后ping虚拟机,发现也ping不通,随后到处找问题。 在本地部分,控制面板 ——>网络和Internet——>网络连接 , 可以看到 VMnet1和Vmnet8虽然都是已…...

Linux cfdisk命令
Linux cfdisk命令用于磁盘分区。 cfdisk是用来磁盘分区的程序,它十分类似DOS的fdisk,具有互动式操作界面而非传统fdisk的问答式界面,您可以轻易地利用方向键来操控分区操作。 语法 cfdisk [-avz][-c <柱面数目>-h <磁头数目>-…...

实用学习网站和资料
github:https://github.com/GitHubDaily/GitHubDaily Linux操作手册: GitHub - abarrak/linux-sysops-handbook: Essentials of Linux system administration. 从零开始制作一个操作系统: GitHub - ruiers/os-tutorial-cn: 从零开始编写一个操作系统…...
【已解决】c++qt如何制作翻译供程序调用
本博文源于笔者正在编写的工具需要创建翻译文件,恰好将qt如何进行翻译,从零到结果进行读者查阅,并非常推荐读者进行收藏点赞,因为步步都很清晰,堪称胎教式c制作,而且内容还包括如何部署在windows下。堪称值…...
DPDK单步跟踪(3)-如何利用visual studio 2019和visual gdb来单步调试dpdk
准备工作 因为时间的关系,我想到哪说到哪,可能没那么高的完成度。 但其实有心的人,看到这个标题,就关了本文自己能做了。 why和how to build debug version DPDK,见前两篇。这里我们准备开始。 首先,你有一台linux机…...

Python爬虫---解析---BeautifulSoup
BeautifulSoup简称:bs4 作用:解析和提取数据 1. 安装:pip install bs4 或pip install bs4 -i https://pypi.douban.com/simple(使用国内镜像下载) 注意:需要安装在python解释器相同的位置,例如…...

Argument list too long when copying files
for i in /path/to/dir/*; do cp "$i" /path/to/other/dir/; done...

configure
configure 配置软件./configure --prefix$PWD/output CCaarch64-linux-gcc --hostaarch64-linux --enable-shared --enable-staticconfig.sub 文件 这个文件用于确定主机系统的类型,并返回与该系统相关的标识符。它包含一系列 shell 函数,用于检测主机…...
HOJ 项目部署-前端定制 默认勾选显示标签、 在线编辑器主题和字号大小修改、增加一言功能 题目AC后礼花绽放
# 项目拉取地址: https://gitee.com/himitzh0730/hoj.git # 切换到hoj-vue目录执行以下命令 #安装依赖 npm install #运行服务 npm run serve #修改代码后构建项目到dist文件夹,到服务器docker-compose.yml中修改hoj-frontend文件映射即可 npm run build…...
)
Scikit-Learn线性回归(二)
Scikit-Learn线性回归二:多项式回归 1、多项式回归2、多项式回归的原理3、Scikit-Learn多项式回归3.1、Scikit-Learn多项式回归API1、多项式回归 线性回归研究的是一个自变量与一个因变量之间的回归问题。在实际应用中,并不是所有的情景都符合线性关系,大多数情况都是非线性…...

07 Vue3框架简介
文章目录 一、Vue3简介1. 简介2. 相关网站3. 前端技术对比4. JS前端框架5. Vue核心内容6. 使用方式 二、基础概念1. 创建一个应用2. 变量双向绑定(v-model)3. 条件控制(v-if)4. 数组遍历(v-for)5. 绑定事件…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...

sshd代码修改banner
sshd服务连接之后会收到字符串: SSH-2.0-OpenSSH_9.5 容易被hacker识别此服务为sshd服务。 是否可以通过修改此banner达到让人无法识别此服务的目的呢? 不能。因为这是写的SSH的协议中的。 也就是协议规定了banner必须这么写。 SSH- 开头,…...