leetcode——打家劫舍问题汇总
本章汇总一下leetcode中的打家劫舍问题,使用经典动态规划算法求解。
1、梦开始的地方——打家劫舍(★)

本题关键点就是不能在相邻房屋偷东西。
采用常规动态规划做法:
- 根据题意设定dp数组,dp[i]的含义为:前i个房屋内,能偷的最高金额。
- 需要初始化dp[0]=0,dp[1]=nums[0]。
- 遍历dp数组,对应两种情况:偷或者不偷。 递推公式为:
-
dp[i] = Math.max(dp[i-1] , dp[i-2]+nums[i-1]);
-
-
最后返回dp数组最后一个数。
java代码如下:
class Solution {public int rob(int[] nums) {if(nums.length == 1) return nums[0];int[] dp = new int[nums.length+1]; //dp[i]:前i个房屋内,能偷的最高金额。dp[1] = nums[0];for(int i=2; i<=nums.length; i++){dp[i] = Math.max(dp[i-1] , dp[i-2]+nums[i-1]); //分别对应偷或者不偷}return dp[nums.length];}
}2、打家劫舍II

本题是上一题的进阶版,区别在于收尾两个房屋也是相邻的,不能同时偷。 此时无非就两种情况:
- 不偷首房屋。
- 不偷尾房屋。
分别设两个dp数组对应以上两种情况即可,思路还是类似上一题。
java代码如下:
class Solution {public int rob(int[] nums) {if(nums.length == 1) return nums[0];int[] dp1 = new int[nums.length]; //不偷首房屋int[] dp2 = new int[nums.length]; //不偷尾房屋dp1[1] = nums[1];dp2[1] = nums[0];for(int i=2; i<nums.length; i++){dp1[i] = Math.max(dp1[i-1] , dp1[i-2]+nums[i]);dp2[i] = Math.max(dp2[i-1] , dp2[i-2]+nums[i-1]);}return dp1[nums.length-1] > dp2[nums.length-1] ? dp1[nums.length-1] : dp2[nums.length-1];}
}3、打家劫舍III(★)
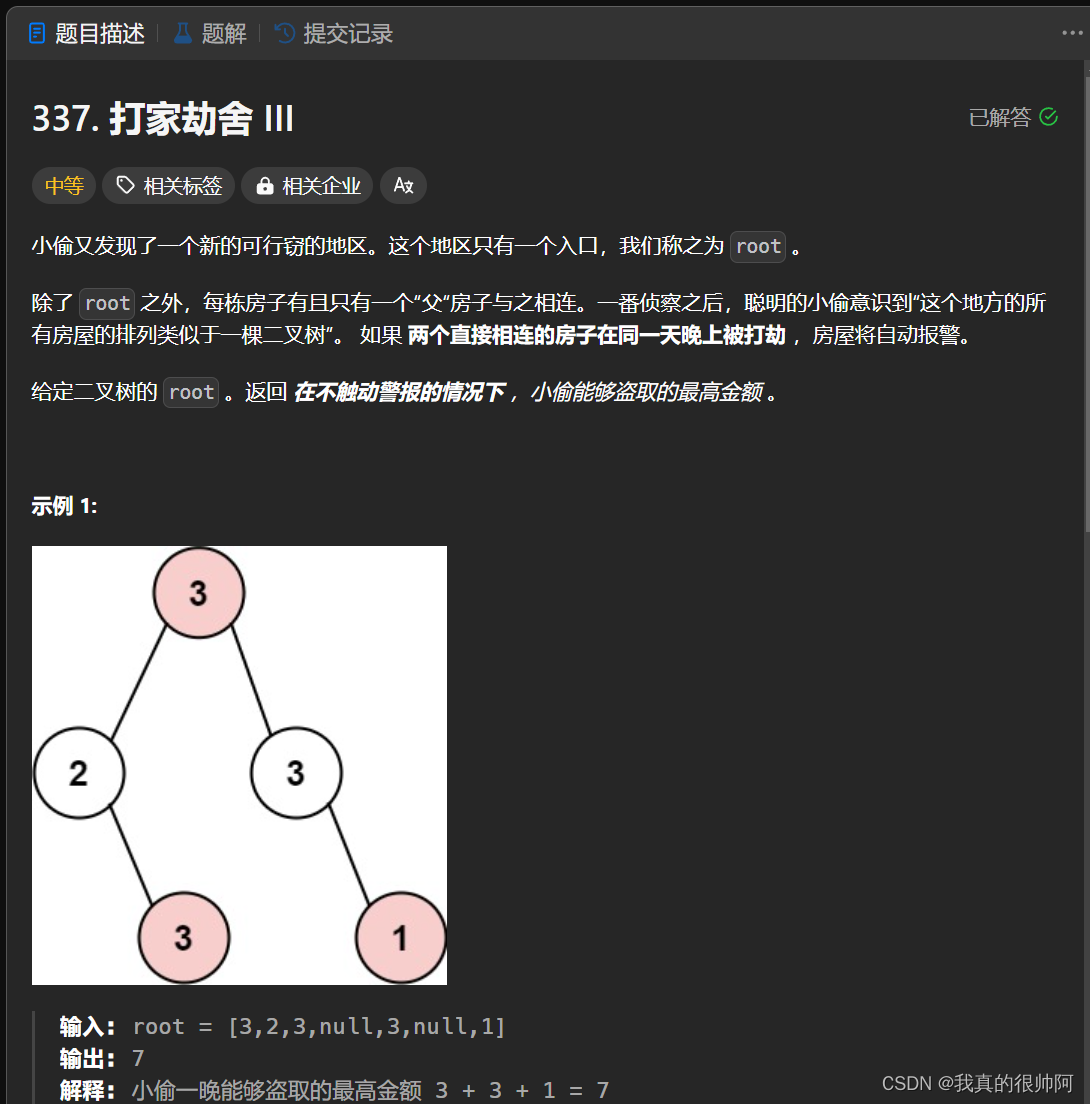
本题是从数组型dp转化为树形dp,由于父节点的状态需要从孩子节点的状态推出来,因此需要使用后序遍历。
首先需要定义一个递归函数dfs,参数为当前节点,返回值为长度为2的数组,即dp数组,dp[0]代表选当场节点,dp[1]代表不选当前节点。 如下:
int[] dfs(TreeNode node)
接下来确定终止条件:
if(node == null) return new int[] {0,0};
使用后序遍历递归遍历左右子树:
//递归左右子树
int[] left = dfs(node.left);
int[] right = dfs(node.right);
确定单层递归逻辑:
//分别对应偷与不偷的情况:
int rob = node.val + left[1] + right[1];
int no_rob = Math.max(left[0],left[1]) + Math.max(right[0],right[1]);
java代码如下:
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public int rob(TreeNode root) {int[] ans = dfs(root);return Math.max(ans[0],ans[1]);}private int[] dfs(TreeNode node){if(node == null) return new int[] {0,0};//递归左右子树int[] left = dfs(node.left);int[] right = dfs(node.right);int rob = node.val + left[1] + right[1];int no_rob = Math.max(left[0],left[1]) + Math.max(right[0],right[1]);return new int[] {rob,no_rob};}
}
相关文章:

leetcode——打家劫舍问题汇总
本章汇总一下leetcode中的打家劫舍问题,使用经典动态规划算法求解。 1、梦开始的地方——打家劫舍(★) 本题关键点就是不能在相邻房屋偷东西。 采用常规动态规划做法: 根据题意设定dp数组,dp[i]的含义为:…...
Java经典框架之Spring MVC
Spring MVC Java 是第一大编程语言和开发平台。它有助于企业降低成本、缩短开发周期、推动创新以及改善应用服务。如今全球有数百万开发人员运行着超过 51 亿个 Java 虚拟机,Java 仍是企业和开发人员的首选开发平台。 课程内容的介绍 1. Spring MVC 入门案例 2. 基…...

Golang make vs new
文章目录 1.简介2.区别3.new 可以初始化 slice,map 和 channel 吗?4.make 可以初始化其他类型吗?5.小结参考文献 1.简介 在 Go 语言中,make 和 new 是两个用于创建对象的内建函数,但它们有着不同的用途和适用范围。 …...

Arthas
概述 Arthas(阿尔萨斯) 能为你做什么? Arthas 是Alibaba开源的Java诊断工具,深受开发者喜爱。 当你遇到以下类似问题而束手无策时,Arthas可以帮助你解决: 这个类从哪个 jar 包加载的?为什么会…...

IP代理科普| 共享IP还是独享IP?两者的区别与优势
通俗地讲,共享IP就像乘坐公共汽车一样,您可以到达目的地,但将与其他乘客共享旅程,座位很可能是没有的。独享IP就像坐出租车一样,您可以更快到达目的地,由于车上只有您一个人,座位是您一个人专用…...
龙芯loongarch64服务器编译安装tensorflow-io-gcs-filesystem
前言 安装TensorFlow的时候,会出现有些包找不到的情况,直接使用pip命令也无法安装,比如tensorflow-io-gcs-filesystem,安装的时候就会报错: 这个包需要自行编译,官方介绍有限,这里我讲解下 编译 准备 拉取源码:https://github.com/tensorflow/io.git 文章中…...

开源持续测试平台Linux MeterSphere本地部署与远程访问
文章目录 前言1. 安装MeterSphere2. 本地访问MeterSphere3. 安装 cpolar内网穿透软件4. 配置MeterSphere公网访问地址5. 公网远程访问MeterSphere6. 固定MeterSphere公网地址 前言 MeterSphere 是一站式开源持续测试平台, 涵盖测试跟踪、接口测试、UI 测试和性能测试等功能&am…...

Kubernetes(K8S)快速入门
概述 在本门课程中,我们将会学习K8S一些非常重要和核心概念,已经操作这些核心概念对应组件的相关命令和方式。比如Deploy部署,Pod容器,调度器,Service服务,Node集群节点,Helm包管理器等等。 在…...
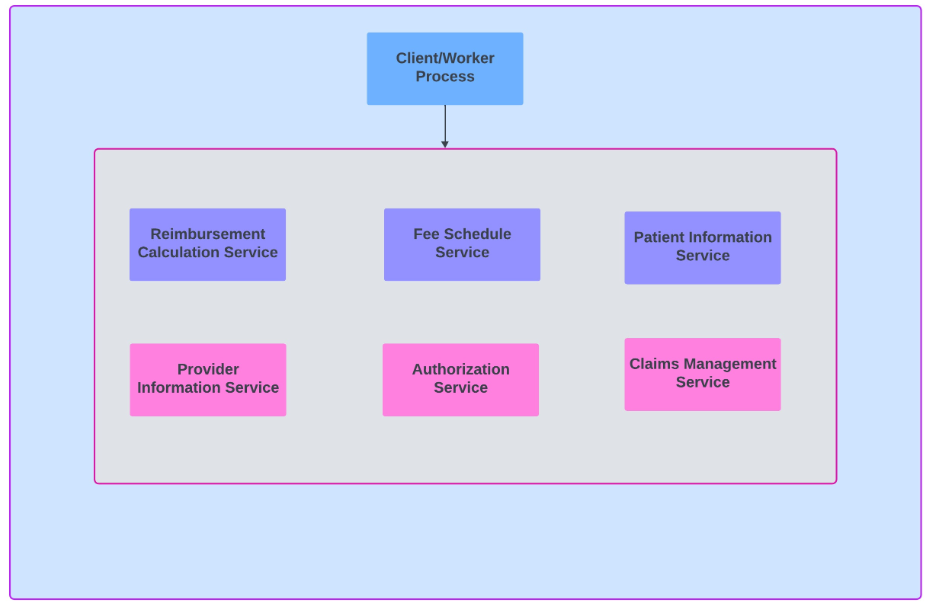
将遗留系统分解为微服务:第 2 部分
在当今不断发展的技术环境中,从整体架构向微服务的转变对于许多企业来说都是一项战略举措。这在报销计算系统领域尤其重要。正如我在上一篇文章第 1 部分应用 Strangler 模式将遗留系统分解为微服务-CSDN博客中提到的,让我们探讨如何有效管理这种转变。 …...

RK3588平台开发系列讲解(AI 篇)RKNN-Toolkit2 模型的加载转换
文章目录 一、Caffe 模型加载接口二、TensorFlow 模型加载接口三、TensorFlowLite 模型加载接口四、ONNX 模型加载五、DarkNet 模型加载接口六、PyTorch 模型加载接口沉淀、分享、成长,让自己和他人都能有所收获!😄 📢 RKNN-Toolkit2 目前支持 Caffe、TensorFlow、Tensor…...
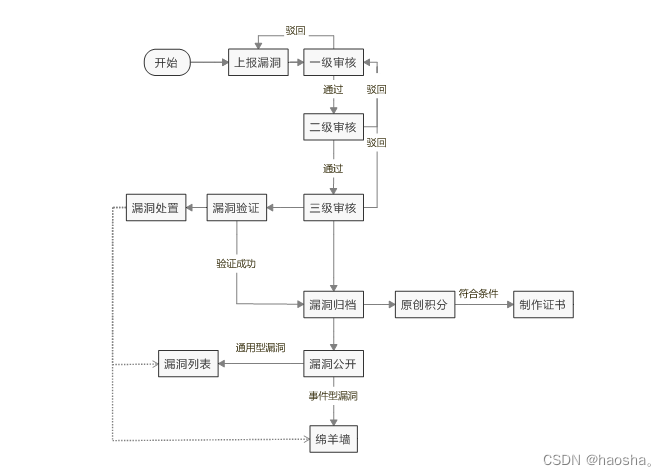
CNVD原创漏洞审核和处理流程
一、CNVD原创漏洞审核归档和发布主流程 (一)审核和归档流程 审核流程分为一级、二级、三级审核,其中一级审核主要对提交的漏洞信息完整性进行审核,漏洞符合可验证(通用型漏洞有验证代码信息或多个互联网实例、事件型…...
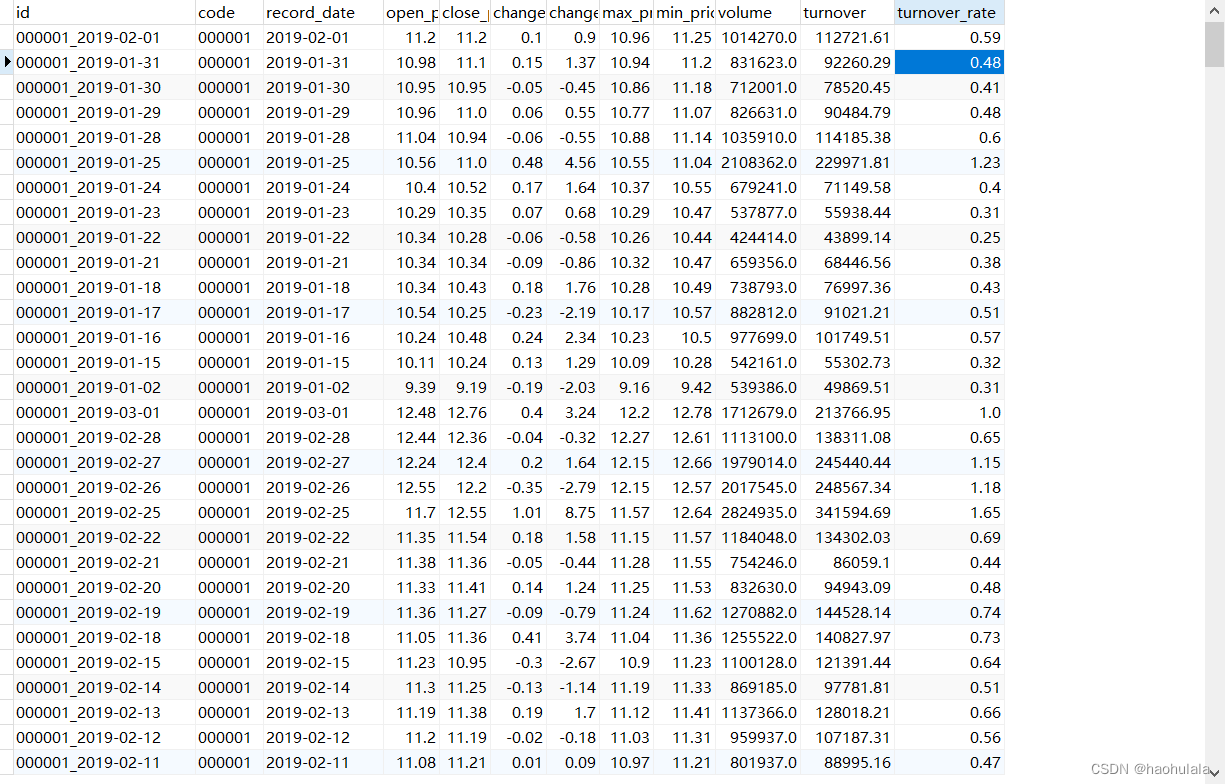
【java爬虫】基于springboot+jdbcTemplate+sqlite+OkHttp获取个股的详细数据
注:本文所用技术栈为:springbootjdbcTemplatesqliteOkHttp 前面的文章我们获取过沪深300指数的成分股所属行业以及权重数据,本文我们来获取个股的详细数据。 我们的数据源是某狐财经,接口的详细信息在下面的文章中,本…...

智能优化算法应用:基于人工兔算法3D无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于人工兔算法3D无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于人工兔算法3D无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.人工兔算法4.实验参数设定5.算法结果6.参考文…...
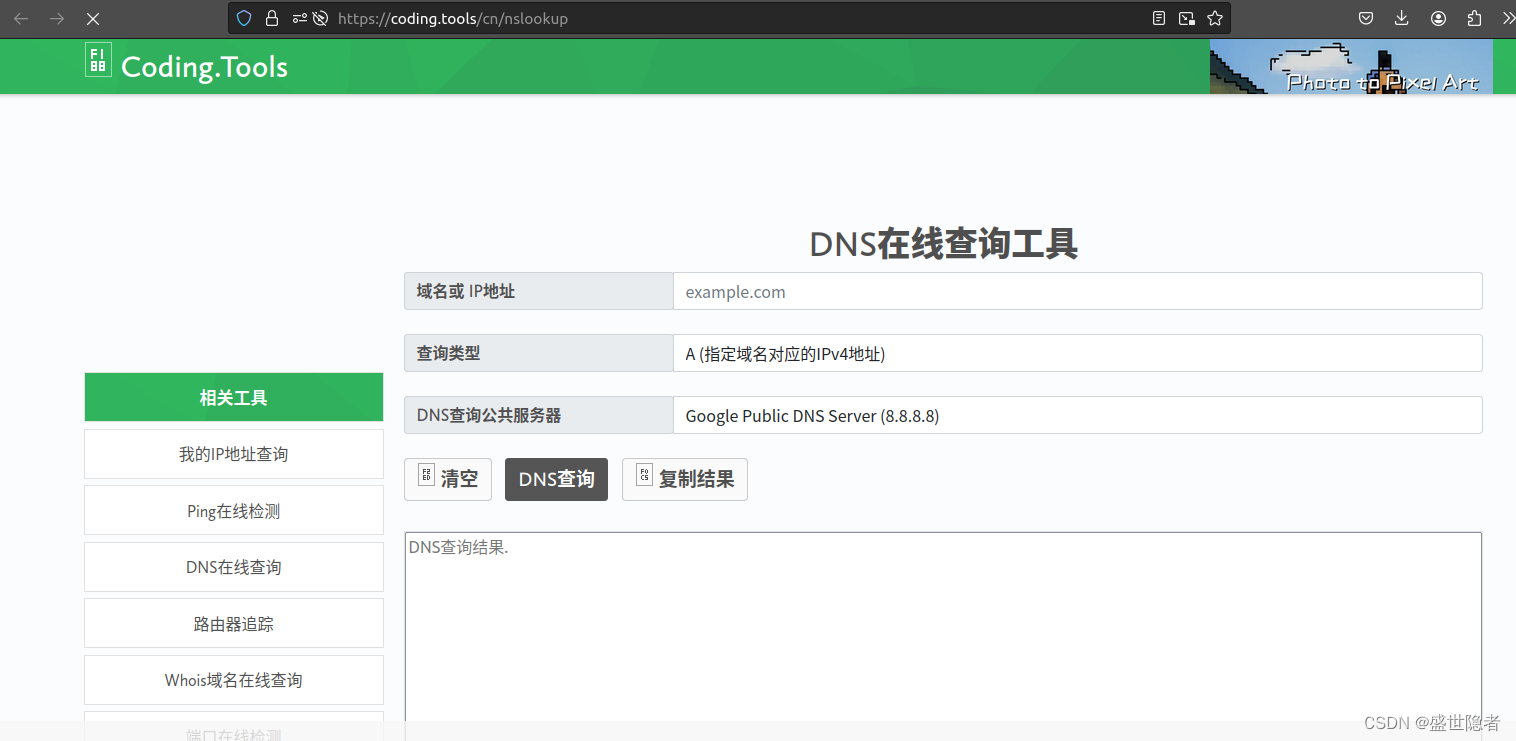
【ubuntu 22.04】安装vscode并配置正常访问应用商店
注意:要去vscode官网下载deb安装包,在软件商店下载的版本不支持输入中文 在ubuntu下用火狐浏览器无法访问vscode官网,此时可以手动进行DNS解析,打开DNS在线查询工具,解析以下主机地址(复制最后一个IP地址&a…...

K8s出现问题时,如何排查解决!
K8s问题的排查 1. POD启动异常、部分节点无法启动pod2. 审视集群状态3. 追踪事件日志4. 聚焦Pod状态5. 检查网络连通性6. 审视存储配置7. 研究容器日志8. K8S集群网络通信9. 问题:Service 是否通过 DNS 工作?10. 总结1、POD启动异常、部分节点无法启动p…...

2015年第四届数学建模国际赛小美赛B题南极洲的平均温度解题全过程文档及程序
2015年第四届数学建模国际赛小美赛 B题 南极洲的平均温度 原题再现: 地表平均温度是反映气候变化和全球变暖的重要指标。然而,在以前的估计中,在如何界定土地平均数方面存在一些方法上的差异。为简单起见,我们只考虑南极洲。请建…...

npm常见错误
三个方面 1. npm ERR! code ELIFECYCLE npm ERR! errno 1 npm ERR! code ELIFECYCLE npm ERR! errno 1 npm ERR! phantomjs-prebuilt2.1.15 install: node install.js npm ERR! Exit status 1 npm ERR! npm ERR! Failed at the phantomjs-prebuilt2.1.15 install script. np…...

JVM入门到入土-Java虚拟机寄存器指令集与栈指令集
JVM入门到入土-Java虚拟机寄存器指令集与栈指令集 HotSpot虚拟机中的任何操作都需要入栈和出栈的步骤。 由于跨平台性的设计,Java的指令都是根据栈来设计的。不同平台CPU架构不同,所以不能设计为基于寄存器的。优点是跨平台,指令集小&#x…...
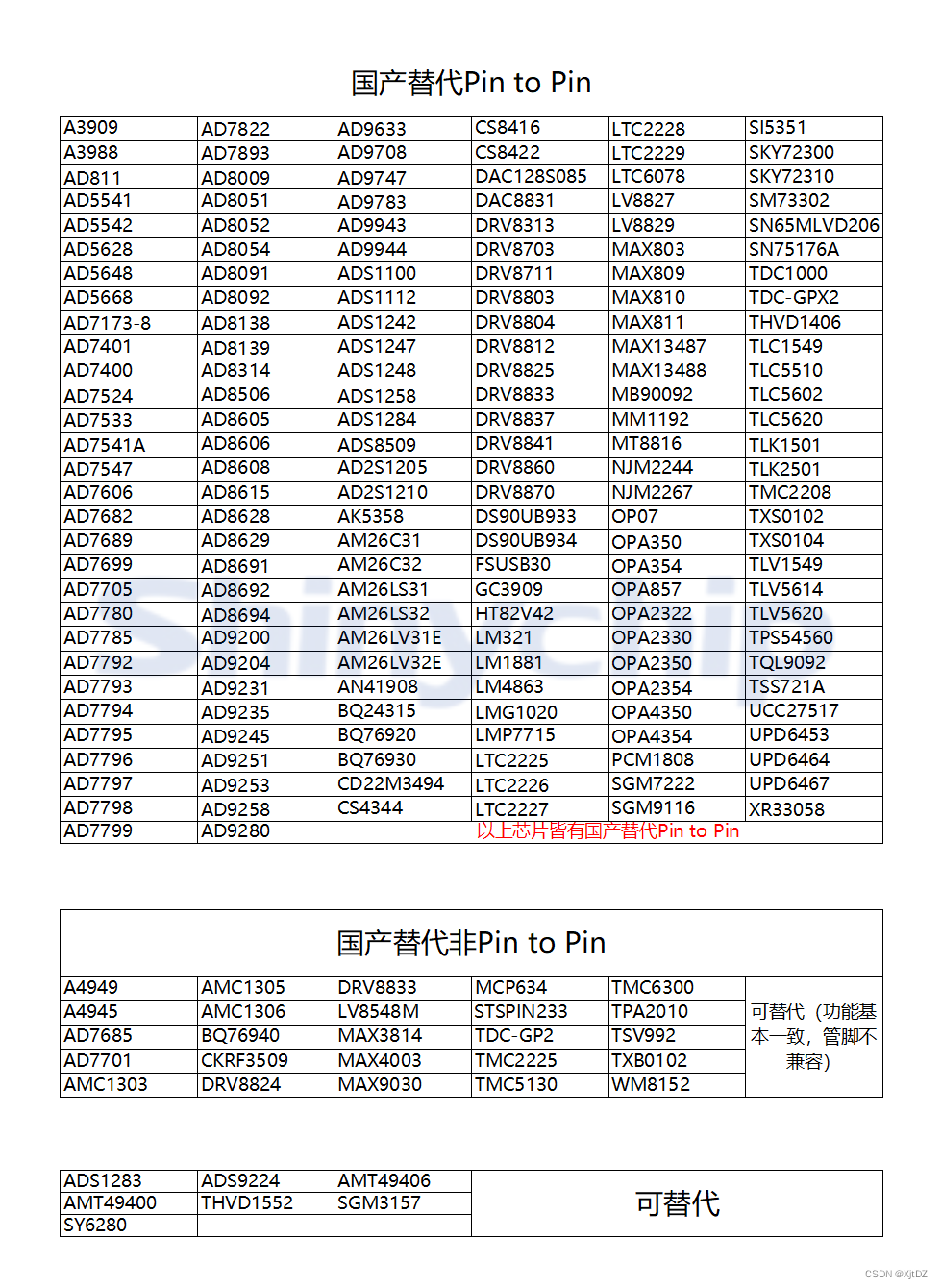
MS2244模拟开关可Pin to Pin兼容NJM2244
MS2244 是一款集成的视频开关,实现三输入视频或音频信号的三选一。可Pin to Pin兼容NJM2244。 芯片集成了 75Ω驱动电路,可以直接驱动电视监控器。芯片工作电压 5V~12V,带宽 10MHz,抗串扰 70dB (4.43MHz)。另外芯片还集…...
PostgreSQL 可观测性最佳实践
简介 软件简述 PostgreSQL 是一种开源的关系型数据库管理系统 (RDBMS),它提供了许多可观测性选项,以确保数据库的稳定性和可靠性。 可观测性 可观测性(Observability)是指对数据库状态和操作进行监控和记录,以便在…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...

【Java】Ajax 技术详解
文章目录 1. Filter 过滤器1.1 Filter 概述1.2 Filter 快速入门开发步骤:1.3 Filter 执行流程1.4 Filter 拦截路径配置1.5 过滤器链2. Listener 监听器2.1 Listener 概述2.2 ServletContextListener3. Ajax 技术3.1 Ajax 概述3.2 Ajax 快速入门服务端实现:客户端实现:4. Axi…...

OpenGL-什么是软OpenGL/软渲染/软光栅?
软OpenGL(Software OpenGL)或者软渲染指完全通过CPU模拟实现的OpenGL渲染方式(包括几何处理、光栅化、着色等),不依赖GPU硬件加速。这种模式通常性能较低,但兼容性极强,常用于不支持硬件加速…...

生信服务器 | 做生信为什么推荐使用Linux服务器?
原文链接:生信服务器 | 做生信为什么推荐使用Linux服务器? 一、 做生信为什么推荐使用服务器? 大家好,我是小杜。在做生信分析的同学,或是将接触学习生信分析的同学,<font style"color:rgb(53, 1…...

【threejs】每天一个小案例讲解:创建基本的3D场景
代码仓 GitHub - TiffanyHoo/three_practices: Learning three.js together! 可自行clone,无需安装依赖,直接liver-server运行/直接打开chapter01中的html文件 运行效果图 知识要点 核心三要素 场景(Scene) 使用 THREE.Scene(…...
