【四】【C语言\动态规划】地下城游戏、按摩师、打家劫舍 II,三道题目深度解析
动态规划
动态规划就像是解决问题的一种策略,它可以帮助我们更高效地找到问题的解决方案。这个策略的核心思想就是将问题分解为一系列的小问题,并将每个小问题的解保存起来。这样,当我们需要解决原始问题的时候,我们就可以直接利用已经计算好的小问题的解,而不需要重复计算。
动态规划与数学归纳法思想上十分相似。
数学归纳法:
-
基础步骤(base case):首先证明命题在最小的基础情况下成立。通常这是一个较简单的情况,可以直接验证命题是否成立。
-
归纳步骤(inductive step):假设命题在某个情况下成立,然后证明在下一个情况下也成立。这个证明可以通过推理推断出结论或使用一些已知的规律来得到。
通过反复迭代归纳步骤,我们可以推导出命题在所有情况下成立的结论。
动态规划:
-
状态表示:
-
状态转移方程:
-
初始化:
-
填表顺序:
-
返回值:
数学归纳法的基础步骤相当于动态规划中初始化步骤。
数学归纳法的归纳步骤相当于动态规划中推导状态转移方程。
动态规划的思想和数学归纳法思想类似。
在动态规划中,首先得到状态在最小的基础情况下的值,然后通过状态转移方程,得到下一个状态的值,反复迭代,最终得到我们期望的状态下的值。
接下来我们通过三道例题,深入理解动态规划思想,以及实现动态规划的具体步骤。
174. 地下城游戏

题目解析

状态表示
我们可以定义,dp[i][j]表示从(i,j)位置出发,到达右下角所需的最小生命值。
状态的表示通常是经验+题目来得到的。
经验指的是,以某个位置为结尾,或者以某个位置开始。
这道题目我们选择以(i,j)位置开始到达最后的思路定义状态。
故状态表示为,dp[i][j]表示从(i,j)位置出发,到达右下角所需的最小生命值。
为什么选择这一种方式而不选择从(0,0)位置开始到达(i,j)位置所需的最小生命值?

上图所示,如果我们考虑蓝色和绿色两种路径,
绿色路径「从出发点到当前点的路径和」为 1,「从出发点到当前点所需的最小初始值」为 3。
蓝色路径「从出发点到当前点的路径和」为 −1,「从出发点到当前点所需的最小初始值」为 2。
我们希望「从出发点到当前点的路径和」尽可能大,而「从出发点到当前点所需的最小初始值」尽可能小。这两条路径各有优劣。
在上图中,我们知道应该选取绿色路径,因为蓝色路径的路径和太小,使得蓝色路径需要增大初始值到 4 才能走到终点,而绿色路径只要 3 点初始值就可以直接走到终点。但是如果把终点的 −2 换为 0,蓝色路径只需要初始值 2,绿色路径仍然需要初始值 3,最优决策就变成蓝色路径了。
因此,如果按照从左上往右下的顺序进行动态规划,我们无法直接确定到达 (1,2) 的方案,因为有两个重要程度相同的参数同时影响后续的决策。也就是说,这样的动态规划是不满足「无后效性」的。
于是我们考虑从右下往左上进行动态规划。令 dp[i][j] 表示从坐标 (i,j) 到终点所需的最小初始值。换句话说,当我们到达坐标 (i,j)时,如果此时我们的路径和不小于 dp[i][j],我们就能到达终点。
这是leetcode官方题解中的部分解析。
我们可以得出,如果用以某位置为结尾思路定义状态表示,我们没办法依靠前面的状态准确推导出(i,j)位置的状态,而后续的数据依旧会影响(i,j)位置的状态值,所以这种方式是错误的。在运用动态规划时,必须满足【无后效性】,所以我们选择以某位置开始思路定义状态表示。
当我们选择 以某位置开始思路定义状态表示时,我们前面的状态值并不会影响后面的状态值,可以保证满足【无后效性】,所以这种方式是可以行的。
故状态表示为,dp[i][j]表示从(i,j)位置出发,到达右下角所需的最小生命值。
状态转移方程
我们考虑,(i,j)位置的值能不能由其他的状态值推导得出,dp[i+1][j]表示从(i+1,j)位置出发,到达右下角所需的最小生命值。dp[i][j+1]表示从(i,j+1)位置出发,到达右下角所需的最小生命值。对于(i,j)的状态值,分两种情况,(i,j)房间内的值是正数或者是负数。如果(i,j)房间的值是负数,说明我们到达(i,j)时的最小生命值应该是min(dp[i][j+1],dp[i+1][j])-dungeon[i][j]。如果(i,j)房间的值是正数,说明我们到达(i,j)时的最小生命值应该是min(dp[i][j+1],dp[i+1][j])-dungeon[i][j],但是这样写又会有两种情况,那就是减出来的数是大于零的数或者是小于等于零的数,我们到达(i,j)房间时最小生命不可能是小于等于零的数,而减出来的数是小于等于零意义是,(i,j)的血包特别的大,即使你的血是负数,吃完之后都可以到达终点,所以实际上到达该位置的生命值为最低的1就可以。
故状态转移方程为,
dp[i][j]=min(dp[i+1][j],dp[i][j+1])-dungeon[i][j]
if(dp[i][j]<=0)dp[i][j]=1
初始化
根据状态转移方程,我们如果要推导出(i,j)位置的状态,就需要运用到(i+1,j)和(i,j+1)位置的状态,所以我们为了不越界,需要初始化最后一行和最后一列的数据。我们发现这种初始化有点复杂,所以我们把对这些位置的初始化转化为对虚拟节点的初始化,也就是创建虚拟节点代替原先初始化的位置。

对于红色位置的状态,他们所需访问的虚拟节点的值,是一定不能取到的,根据状态转移方程,
dp[i][j]=min(dp[i+1][j],dp[i][j+1])-dungeon[i][j]
if(dp[i][j]<=0)dp[i][j]=1
所以他们访问的虚拟节点值应该置正无穷,这样取最小就不会取到。
对于紫色位置的状态,他的状态值应该是1-dungeon[i][j]所以min(dp[i+1][j],dp[i][j+1])的值应该为1。所有我们可以先把所有位置置正无穷,然后在这两个位置选一个位置置1就可以了。

填表顺序
从右到左,从下到上
返回值
返回dp[0][0]
代码实现
int calculateMinimumHP(int** dungeon, int dungeonSize, int* dungeonColSize) {int row=dungeonSize;int col=dungeonColSize[0];int dp[row+1][col+1];for(int i=0;i<=row;i++){memset(dp[i],0x3f,sizeof(dp[i]));}dp[row-1][col]=1;for(int i=row-1;i>=0;i--){for(int j=col-1;j>=0;j--){dp[i][j]=fmin(dp[i][j+1],dp[i+1][j])-dungeon[i][j];if(dp[i][j]<=0) dp[i][j]=1;}}return dp[0][0];
} for(int i=0;i<=row;i++){memset(dp[i],0x3f,sizeof(dp[i]));}void *memset(void *s, int ch, size_t n);
函数解释:将s中前n个字节 (typedef unsigned int size_t )用 ch 替换并返回 s 。
memset:作用是在一段内存块中填充某个给定的值,它是对较大的结构体或数组进行清零操作的一种最快方法。

![]()
_itoa可以把x值转化为char类型的2进制数存放在string中。
我们发现x的二进制数是00111111 00111111 00111111 00111111。
用_itoa转换二进制数时,前导零省略了,实际上是00111111 00111111 00111111 00111111。
一个int类型占4个字节。
一个字节占8位二进制数。
而0x3f的二进制数是00111111。
memset的意思是,将x中前n个字节,用0x3f最后一个字节对应的二进制数替换。
那为什么要赋值0x3f:
作为无穷大使用
因为4个字节均为0x3f时,0x3f3f3f3f的十进制是1061109567,也就是10^ 9级别的(和0x7fffffff一个数量级),而一般场合下的数据都是小于10^9的,所以它可以作为无穷大使用而不致出现数据大于无穷大的情形。
可以保证无穷大加无穷大仍然不会超限。
另一方面,由于一般的数据都不会大于10^9,所以当我们把无穷大加上一个数据时,它并不会溢出(这就满足了“无穷大加一个有穷的数依然是无穷大”),事实上0x3f3f3f3f+0x3f3f3f3f=2122219134,这非常大但却没有超过32-bit int的表示范围,所以0x3f3f3f3f还满足了我们“无穷大加无穷大还是无穷大”的需求。
面试题 17.16. 按摩师
题目解析

状态表示
我们可以定义dp[i]表示,从nums[0]开始一直到nums[i],选择不相邻的预约情况中,最长的时间数。
状态转移方程
我们想一想dp[i]能不能由其他的状态推导得出。
dp[i]表示,从nums[0]开始一直到nums[i],选择不相邻的预约情况中,最长的时间数。
dp[i-1]表示,从nums[0]开始一直到nums[i-1],选择不相邻的预约情况中,最长的时间数。
dp[i-2]表示,从nums[0]开始一直到nums[i-2],选择不相邻的预约情况中,最长的时间数。
如果i位置预约我们选择,那么i-1位置预约肯定不选择,这种情况对应的最长时间数就是
dp[i-2]+nums[i]
如果i位置预约我们不选择,这种情况对应的最长时间数就是
dp[i-1]
因为我们存储是最长时间数,所以需要从两种情况中选一个时间更长的。
故状态转移方程为,dp[i]=max(dp[i-2]+nums[i],dp[i-1])
初始化
根据状态转移方程,我们推导出i位置的状态需要用到(i-2)和(i-1)的状态值。
我们想要统一所有需要得到的状态,都通过状态转移方程推导得出,那么我们就需要创建虚拟节点替代需要初始化的位置。
创建虚拟节点有几点注意事项,
第一,对虚拟节点的初始化必须保证后续的推导过程不出错。
第二,注意下标映射关系的变化,也就是状态表示和状态转移方程的下标变换。

状态转移方程为,dp[i]=max(dp[i-2]+nums[i-2],dp[i-1])。
对于紫色第一个状态值,应该是填自己的时间数,所以需要选择dp[i-2]+nums[i-2]且dp[n-2]需要为零,即dp[0]为0。
对于紫色第二个状态值,要么是填自己的值,要么填紫色第一个状态值。
所以dp[i-2]为零,即dp[1]。
故初始化为dp[0]=dp[1]=0。
填表顺序
从左往右
返回值
放回最后一个元素的值,dp[n+1]
n是nums的数组大小
代码实现
int massage(int* nums, int numsSize){int n=numsSize;int dp[n+2];memset(dp,0,sizeof(dp));for(int i=2;i<=n+1;i++){dp[i]=fmax(dp[i-2]+nums[i-2],dp[i-1]);}return dp[n+1];
}
213. 打家劫舍 II

题目解析


我们可以把问题分成两种情况,要么数组的长度大于1,要么数组的长度等于1。
当数组的长度大于1时,我们有两种情况。
第一,我们考虑第一个房子,不考虑最后一个房子。
第二,我们不考虑第一个房子,考虑最后一个房子。
这样问题就转化为普通的不环绕的问题了。
当数组的长度等于1时,我们只能选择nums[0],这一个房子。
所以我们只需要解决不环绕的问题即可。
状态表示
我们可以定义dp[i]表示从nums[0]开始到nums[i]这些房子,选择不相邻房子方法数中金额最大的金额数。
状态转移方程
我们想一想dp[i]能不能由其他状态推导得出。
dp[i]表示从nums[0]开始到nums[i]这些房子,选择不相邻房子方法数中金额最大的金额数。
dp[i-1]表示从nums[0]开始到nums[i-1]这些房子,选择不相邻房子方法数中金额最大的金额数。
dp[i-2]表示从nums[0]开始到nums[i-2]这些房子,选择不相邻房子方法数中金额最大的金额数。
对dp[i]这个状态进行分析,如果该房子选择的话,i-1房子就不能选择,所以这种情况下金额最大数为dp[i-2]+nums[i]
如果该房子不选择的话,最大金额数就是dp[i-1]
故状态转移方程为,dp[i]=max(dp[i-2]+nums[i],dp[i-1])
初始化
根据状态转移方程,我们推导出i位置的状态需要用到(i-2)和(i-1)的状态值。
我们想要统一所有需要得到的状态,都通过状态转移方程推导得出,那么我们就需要创建虚拟节点替代需要初始化的位置。
创建虚拟节点有几点注意事项,
第一,对虚拟节点的初始化必须保证后续的推导过程不出错。
第二,注意下标映射关系的变化,也就是状态表示和状态转移方程的下标变换。

状态转移方程为,dp[i]=max(dp[i-2]+nums[i-2],dp[i-1])。
对于紫色第一个状态值,应该是填自己的时间数,所以需要选择dp[i-2]+nums[i-2]且dp[n-2]需要为零,即dp[0]为0。
对于紫色第二个状态值,要么是填自己的值,要么填紫色第一个状态值。
所以dp[i-2]为零,即dp[1]。
故初始化为dp[0]=dp[1]=0。
填表顺序
从左往右
返回值
分两种情况,计算当长度大于1时,考虑第一个房子而不考虑最后一个房子的金额数,
和当长度大于1时,不考虑第一个房子而考虑最后一个房子的金额数。
和当长度为1时,nums[0]的金额数
返回三者中最大的金额数即可。
代码实现
int rob_(int* nums,int numsSize, int left,int right) {int n=numsSize;int dp[n+2];memset(dp,0,sizeof(dp));for(int i=left;i<=right;i++){dp[i]=fmax(dp[i-2]+nums[i-2],dp[i-1]);}return dp[right];
}
int rob(int* nums,int numsSize){int num1=rob_(nums,numsSize,2,numsSize);int num2=rob_(nums,numsSize,3,numsSize+1);return fmax(fmax(num1,num2),nums[0]);
}我们rob_函数就是解决不环绕的一列房子问题。
接着把环绕的问题转化为不环绕的问题。
如果数组的长度大于1。
如果我们考虑第一个房子,而不考虑最后一个房子,只需要填写dp表中下标2到下标numsSize状态的推导填写。
如果我们不考虑第一个房子,而考虑最后一个房子,只需要填写dp表中下标3到下标numsSize+1的状态的推导填写。
如果数组的长度等于1。
考虑nums[0]的金额数。
如果数组长度为1,num1和num2计算出来的值都是零,因为numsSize 为1,而循环是从下标2开始或者从下标3开始,所以最后的返回值是初始化的零。
此时只需要返回nums[0]即可,nums [0]一定大于0。
所以返回比较num1,num2和nums[0]即可。
结尾
今天我们学习了动态规划的思想,动态规划思想和数学归纳法思想有一些类似,动态规划在模拟数学归纳法的过程,已知一个最简单的基础解,通过得到前项与后项的推导关系,由这个最简单的基础解,我们可以一步一步推导出我们希望得到的那个解,把我们得到的解依次存放在dp数组中,dp数组中对应的状态,就像是数列里面的每一项。最后感谢您阅读我的文章,对于动态规划系列,我会一直更新,如果您觉得内容有帮助,可以点赞加关注,以快速阅读最新文章。
最后,感谢您阅读我的文章,希望这些内容能够对您有所启发和帮助。如果您有任何问题或想要分享您的观点,请随时在评论区留言。
同时,不要忘记订阅我的博客以获取更多有趣的内容。在未来的文章中,我将继续探讨这个话题的不同方面,为您呈现更多深度和见解。
谢谢您的支持,期待与您在下一篇文章中再次相遇!
相关文章:

【四】【C语言\动态规划】地下城游戏、按摩师、打家劫舍 II,三道题目深度解析
动态规划 动态规划就像是解决问题的一种策略,它可以帮助我们更高效地找到问题的解决方案。这个策略的核心思想就是将问题分解为一系列的小问题,并将每个小问题的解保存起来。这样,当我们需要解决原始问题的时候,我们就可以直接利…...

【大数据存储与处理】开卷考试总复习笔记
文章目录 实验部分一、 HBase 的基本操作1. HBase Shell入门2. HBase创建数据库表3. HBase数据操作4. HBase删除数据库表5. HBase Python基本编程 before二、 HBase 过滤器操作1.创建表和插入数据2.行键过滤器3.列族与列过滤器4.值过滤器5.其他过滤器6.python hbase 过滤器编程…...
)
HTML 实操试题(一)
创建一个包含标题、段落和链接的基本HTML文档: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><ti…...
)
创龙瑞芯微RK3568设备树1(修改设备树GPIO和串口)
前言 最近一直在搞3568的东西,涉及到底层的设备树修改,驱动编写等等,忙的焦头烂额的,也没时间往下面写东西了。今天差不多底层的东西快弄完了,把最近的感悟给大家分享下,并且加入点设备树的基础知识。给刚刚…...

R语言【dplyr】——filter保留符合筛选条件的行,以数据的行为单位,创建子集
Package dplyr version 1.1.4 Parameters filter(.data, ..., .by NULL, .preverse FALSE) 参数【.data】:一个数据集(data frame),数据集扩展(比如:tibble),或者 lazy data fra…...
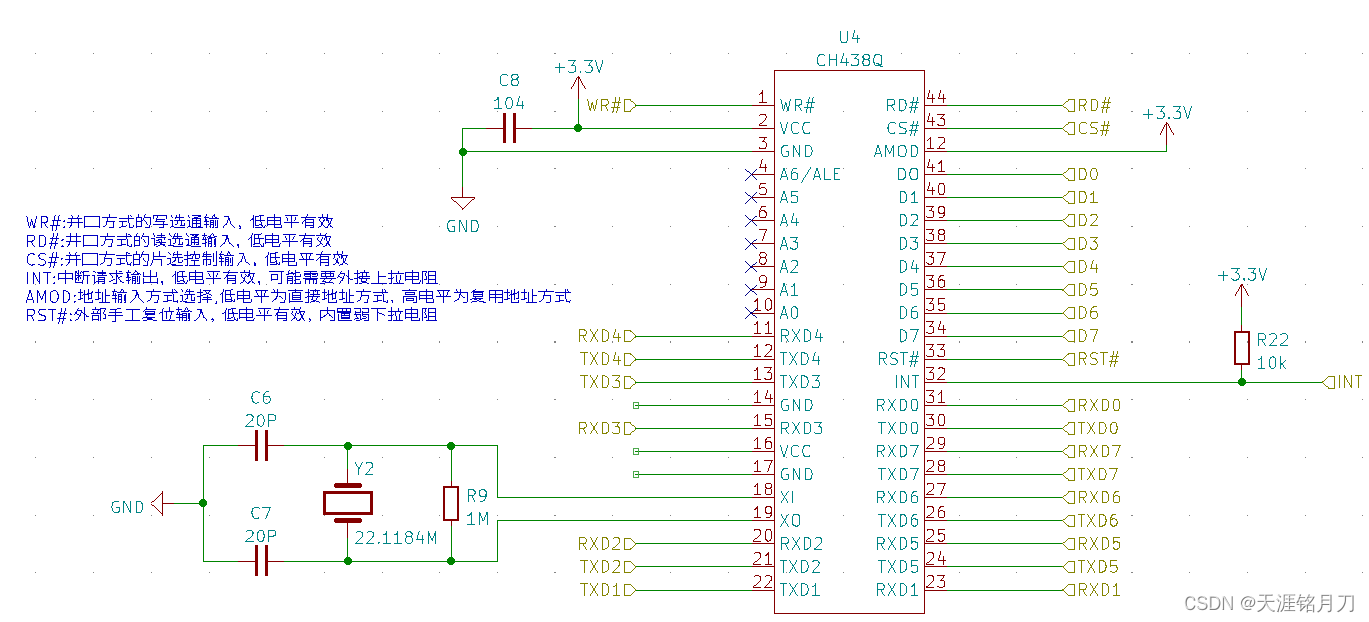
几种串口扩展电路
一、IIC串口扩展电路 LCT200 是一款可以通过 I2C 接口通讯,拓展 2 路独立串口的通讯芯片,同时也支持通过 2 路串口读写 I2C 接口的数据。LCT200 的封装为 TSSOP-20。 主要功能:⚫ 通过对 I2C 接口读写实现拓展 2 路独立串口功能 ⚫ 通过读写…...

实战10 角色管理
目录 1、角色后端接口 2、角色列表查询 2.1 效果图 2.2页面原型代码 2.3 角色api代码 role.js 2.4 查询角色列表代码 4、 新增和编辑角色 5、删除角色 6、分配权限 6.1 分配权限思路 6.2 分配权限回显接口 6.3 分配权限回显前端实现 6.4分配权限后端接口 6.4.1 R…...

Lua的底层原理与C#交互原理浅析【更新中】
目录 lua底层原理浅析 table底层原理浅析 Lua表的C语言定义 原理和实现 userdata lua和C#的交互机制(更新中) 基本介绍 Lua 与 C/C 的数据交互 Lua 调用 C/C 函数 C/C 调用 Lua 函数 基元类型传递 对象类型传递 Lua 调用 C# 总结 网上有很…...
鸿蒙项目二—— 注册和登录
此部分和上篇文章是连续剧 ,如果需要,请查看 一、注册 import http from ohos.net.http; Entry Component struct Reg {// 定义数据:State username: string "";State userpass: string "";State userpass2: string …...
Dijkstra(迪杰斯特拉)算法总结
知识概览 Dijkstra算法适用于解决所有边权都是正数的最短路问题。Dijkstra算法分为朴素的Dijkstra算法和堆优化版的Dijkstra算法。朴素的Dijkstra算法时间复杂度为,适用于稠密图。堆优化版的Dijkstra算法时间复杂度为,适用于稀疏图。稠密图的边数m和是一…...

设计模式?!
如何解决复杂性 链接:不同的设计模式实例代码(更新中) 分解 人们面对复杂性有一个常见的做法:即分而治之,将大问题分解为多个小问题,将复杂问题分解为多个简单问题。 抽象 更高层次来讲,人们处…...

Pytorch项目,肺癌检测项目之三
成功获取到数据之后,我们需要将数据放到Pytorch里面去处理,我们需要将其转换成Dataset数据集,方便去使用相同的API。要转换成Dataset数据集需要实现两个方法,方法一: 方法二: 运行比较慢的话,…...
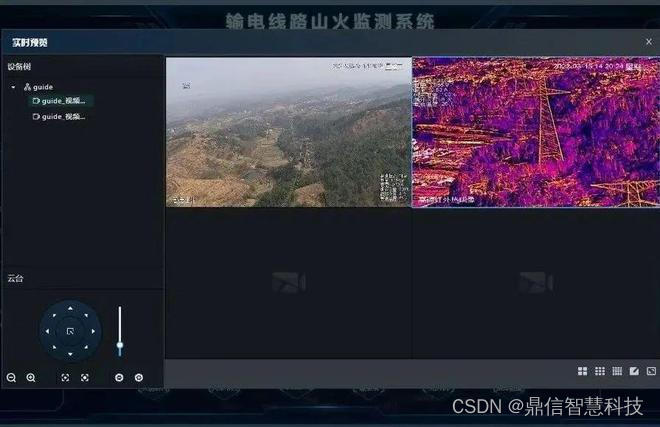
深圳鼎信|输电线路防山火视频监控预警装置:森林火灾来袭,安全不留白!
受线路走廊制约和环保要求影响,输电线路大多建立在高山上,不仅可以减少地面障碍物和人类活动的干扰,还能提高线路的抗灾能力和可靠性。但同时也会面临其它的难题,例如森林火灾预防。今天,深圳鼎信智慧将从不同角度分析…...

【Bash/Shell】知识总结
文章目录 1. 总体认识1.1. Shell概述1.2. 第一个Shell脚本1.3. 注释 2. 变量2.1. 定义变量2.2. 使用变量2.3. 只读变量2.4. 删除变量2.5. 变量类型2.5.1. 字符串变量2.5.2. 整数变量2.5.3. 数组变量2.5.4. 环境变量2.5.5. 特殊变量 3. 输出3.1. echo命令3.2. printf命令 4. 运算…...

单例模式(C++实现)
RAII运用 只能在栈上创建对象 只能在堆上创建的对象 单例模式 设计模式 懒汉模式 解决线程安全 优化 饿汉模式 饿汉和懒汉的区别 线程安全与STL与其他锁...

ElasticSearch 聚合统计
聚合统计 度量聚合:求字段的平均值,最小值,最大值,总和等 桶聚合:将文档分成不同的桶,桶的划分可以根据字段的值,范围,日期间隔 管道聚合:在桶聚合的结果上执行进一步计…...

SpringIOC之MethodBasedEvaluationContext
博主介绍:✌全网粉丝5W+,全栈开发工程师,从事多年软件开发,在大厂呆过。持有软件中级、六级等证书。可提供微服务项目搭建与毕业项目实战,博主也曾写过优秀论文,查重率极低,在这方面有丰富的经验✌ 博主作品:《Java项目案例》主要基于SpringBoot+MyBatis/MyBatis-plus+…...
【网络安全 | 网络协议】结合Wireshark讲解TCP三次握手
前言 TCP(传输控制协议)是一种面向连接的、可靠的传输层协议。在建立 TCP 连接时,需要进行三次握手,防止因为网络延迟、拥塞等原因导致的数据丢失或错误传输,确保双方都能够正常通信。 TCP三次握手在Wireshark数据包中…...

钦丰科技(安徽)股份有限公司携卫生级阀门管件盛装亮相2024发酵展
钦丰科技(安徽)股份有限公司携卫生级阀门管件盛装亮相2024济南生物发酵展! 展位号:2号馆A65展位 2024第12届国际生物发酵产品与技术装备展览会(济南)于3月5-7日在山东国际会展中心盛大召开,展会同期将举办30余场高质…...

Python模拟动态星空
前言 今天,我们来用Python做个星空。 一、模拟星空 1,.首先导入所需要的库: from turtle import * from random import random, randint 2.初始画面: screen Screen() width, height 800, 600 screen.setup(width, height) screen.tit…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...

聚六亚甲基单胍盐酸盐市场深度解析:现状、挑战与机遇
根据 QYResearch 发布的市场报告显示,全球市场规模预计在 2031 年达到 9848 万美元,2025 - 2031 年期间年复合增长率(CAGR)为 3.7%。在竞争格局上,市场集中度较高,2024 年全球前十强厂商占据约 74.0% 的市场…...

UE5 音效系统
一.音效管理 音乐一般都是WAV,创建一个背景音乐类SoudClass,一个音效类SoundClass。所有的音乐都分为这两个类。再创建一个总音乐类,将上述两个作为它的子类。 接着我们创建一个音乐混合类SoundMix,将上述三个类翻入其中,通过它管理每个音乐…...
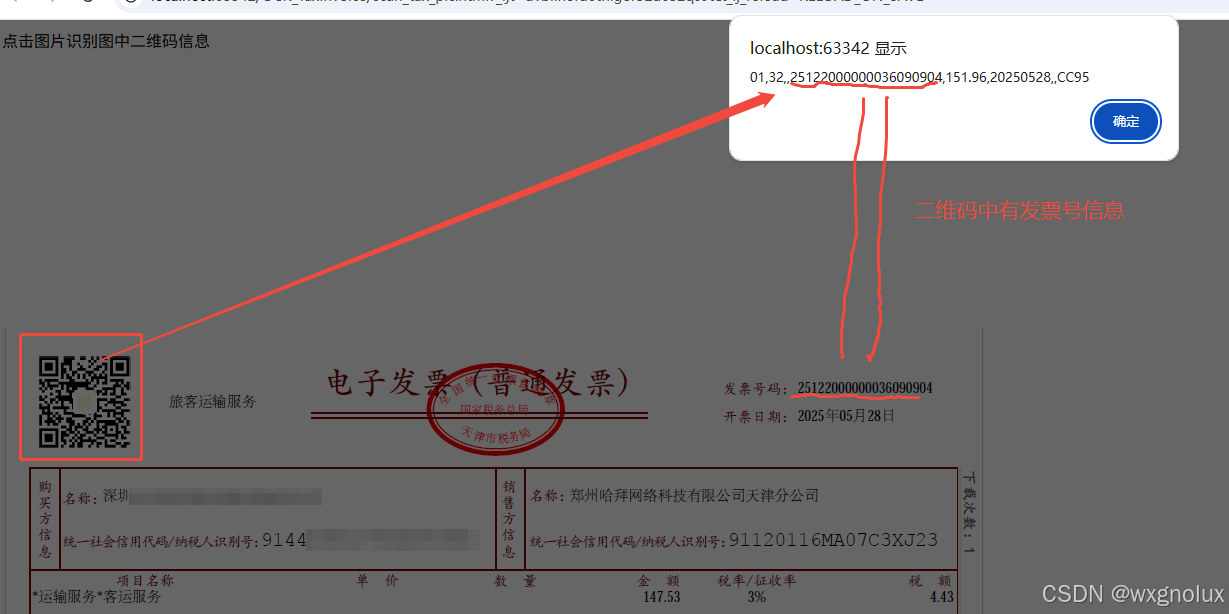
网页端 js 读取发票里的二维码信息(图片和PDF格式)
起因 为了实现在报销流程中,发票不能重用的限制,发票上传后,希望能读出发票号,并记录发票号已用,下次不再可用于报销。 基于上面的需求,研究了OCR 的方式和读PDF的方式,实际是可行的ÿ…...
