【机器学习】【线性回归】梯度下降
文章目录
- @[toc]
- 数据集
- 实际值
- 估计值
- 估计误差
- 代价函数
- 学习率
- 参数更新
- `Python`实现
- 导包
- 数据预处理
- 迭代过程
- 数据可视化
- 完整代码
- 线性拟合结果
- 代价结果
文章目录
- @[toc]
- 数据集
- 实际值
- 估计值
- 估计误差
- 代价函数
- 学习率
- 参数更新
- `Python`实现
- 导包
- 数据预处理
- 迭代过程
- 数据可视化
- 完整代码
- 线性拟合结果
- 代价结果

个人主页:丷从心
系列专栏:机器学习

数据集
( x ( i ) , y ( i ) ) , i = 1 , 2 , ⋯ , m \left(x^{(i)} , y^{(i)}\right) , i = 1 , 2 , \cdots , m (x(i),y(i)),i=1,2,⋯,m
实际值
y ( i ) y^{(i)} y(i)
估计值
h θ ( x ( i ) ) = θ 0 + θ 1 x ( i ) h_{\theta}\left(x^{(i)}\right) = \theta_{0} + \theta_{1} x^{(i)} hθ(x(i))=θ0+θ1x(i)
估计误差
h θ ( x ( i ) ) − y ( i ) h_{\theta}\left(x^{(i)}\right) - y^{(i)} hθ(x(i))−y(i)
代价函数
J ( θ ) = J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 = 1 2 m ∑ i = 1 m ( θ 0 + θ 1 x ( i ) − y ( i ) ) 2 J(\theta) = J(\theta_{0} , \theta_{1}) = \cfrac{1}{2m} \displaystyle\sum\limits_{i = 1}^{m}{\left(h_{\theta}\left(x^{(i)}\right) - y^{(i)}\right)^{2}} = \cfrac{1}{2m} \displaystyle\sum\limits_{i = 1}^{m}{\left(\theta_{0} + \theta_{1} x^{(i)} - y^{(i)}\right)^{2}} J(θ)=J(θ0,θ1)=2m1i=1∑m(hθ(x(i))−y(i))2=2m1i=1∑m(θ0+θ1x(i)−y(i))2
学习率
- α \alpha α是学习率,一个大于 0 0 0的很小的经验值,决定代价函数下降的程度
参数更新
Δ θ j = ∂ ∂ θ j J ( θ 0 , θ 1 ) \Delta{\theta_{j}} = \cfrac{\partial}{\partial{\theta_{j}}} J(\theta_{0} , \theta_{1}) Δθj=∂θj∂J(θ0,θ1)
θ j : = θ j − α Δ θ j = θ j − α ∂ ∂ θ j J ( θ 0 , θ 1 ) \theta_{j} := \theta_{j} - \alpha \Delta{\theta_{j}} = \theta_{j} - \alpha \cfrac{\partial}{\partial{\theta_{j}}} J(\theta_{0} , \theta_{1}) θj:=θj−αΔθj=θj−α∂θj∂J(θ0,θ1)
[ θ 0 θ 1 ] : = [ θ 0 θ 1 ] − α [ ∂ J ( θ 0 , θ 1 ) ∂ θ 0 ∂ J ( θ 0 , θ 1 ) ∂ θ 1 ] \left[ \begin{matrix} \theta_{0} \\ \theta_{1} \end{matrix} \right] := \left[ \begin{matrix} \theta_{0} \\ \theta_{1} \end{matrix} \right] - \alpha \left[ \begin{matrix} \cfrac{\partial{J(\theta_{0} , \theta_{1})}}{\partial{\theta_{0}}} \\ \cfrac{\partial{J(\theta_{0} , \theta_{1})}}{\partial{\theta_{1}}} \end{matrix} \right] [θ0θ1]:=[θ0θ1]−α ∂θ0∂J(θ0,θ1)∂θ1∂J(θ0,θ1)
[ ∂ J ( θ 0 , θ 1 ) ∂ θ 0 ∂ J ( θ 0 , θ 1 ) ∂ θ 1 ] = [ 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x ( i ) ] = [ 1 m ∑ i = 1 m e ( i ) 1 m ∑ i = 1 m e ( i ) x ( i ) ] e ( i ) = h θ ( x ( i ) ) − y ( i ) \left[ \begin{matrix} \cfrac{\partial{J(\theta_{0} , \theta_{1})}}{\partial{\theta_{0}}} \\ \cfrac{\partial{J(\theta_{0} , \theta_{1})}}{\partial{\theta_{1}}} \end{matrix} \right] = \left[ \begin{matrix} \cfrac{1}{m} \displaystyle\sum\limits_{i = 1}^{m}{\left(h_{\theta}\left(x^{(i)}\right) - y^{(i)}\right)} \\ \cfrac{1}{m} \displaystyle\sum\limits_{i = 1}^{m}{\left(h_{\theta}\left(x^{(i)}\right) - y^{(i)}\right) x^{(i)}} \end{matrix} \right] = \left[ \begin{matrix} \cfrac{1}{m} \displaystyle\sum\limits_{i = 1}^{m}{e^{(i)}} \\ \cfrac{1}{m} \displaystyle\sum\limits_{i = 1}^{m}{e^{(i)} x^{(i)}} \end{matrix} \right] \kern{2em} e^{(i)} = h_{\theta}\left(x^{(i)}\right) - y^{(i)} ∂θ0∂J(θ0,θ1)∂θ1∂J(θ0,θ1) = m1i=1∑m(hθ(x(i))−y(i))m1i=1∑m(hθ(x(i))−y(i))x(i) = m1i=1∑me(i)m1i=1∑me(i)x(i) e(i)=hθ(x(i))−y(i)
[ ∂ J ( θ 0 , θ 1 ) ∂ θ 0 ∂ J ( θ 0 , θ 1 ) ∂ θ 1 ] = [ 1 m ∑ i = 1 m e ( i ) 1 m ∑ i = 1 m e ( i ) x ( i ) ] = [ 1 m ( e ( 1 ) + e ( 2 ) + ⋯ + e ( m ) ) 1 m ( e ( 1 ) + e ( 2 ) + ⋯ + e ( m ) ) x ( i ) ] = 1 m [ 1 1 ⋯ 1 x ( 1 ) x ( 2 ) ⋯ x ( m ) ] [ e ( 1 ) e ( 2 ) ⋮ e ( m ) ] = 1 m X T e = 1 m X T ( X θ − y ) \begin{aligned} \left[ \begin{matrix} \cfrac{\partial{J(\theta_{0} , \theta_{1})}}{\partial{\theta_{0}}} \\ \cfrac{\partial{J(\theta_{0} , \theta_{1})}}{\partial{\theta_{1}}} \end{matrix} \right] &= \left[ \begin{matrix} \cfrac{1}{m} \displaystyle\sum\limits_{i = 1}^{m}{e^{(i)}} \\ \cfrac{1}{m} \displaystyle\sum\limits_{i = 1}^{m}{e^{(i)} x^{(i)}} \end{matrix} \right] = \left[ \begin{matrix} \cfrac{1}{m} \left(e^{(1)} + e^{(2)} + \cdots + e^{(m)}\right) \\ \cfrac{1}{m} \left(e^{(1)} + e^{(2)} + \cdots + e^{(m)}\right) x^{(i)} \end{matrix} \right] \\ &= \cfrac{1}{m} \left[ \begin{matrix} 1 & 1 & \cdots & 1 \\ x^{(1)} & x^{(2)} & \cdots & x^{(m)} \end{matrix} \right] \left[ \begin{matrix} e^{(1)} \\ e^{(2)} \\ \vdots \\ e^{(m)} \end{matrix} \right] = \cfrac{1}{m} X^{T} e = \cfrac{1}{m} X^{T} (X \theta - y) \end{aligned} ∂θ0∂J(θ0,θ1)∂θ1∂J(θ0,θ1) = m1i=1∑me(i)m1i=1∑me(i)x(i) = m1(e(1)+e(2)+⋯+e(m))m1(e(1)+e(2)+⋯+e(m))x(i) =m1[1x(1)1x(2)⋯⋯1x(m)] e(1)e(2)⋮e(m) =m1XTe=m1XT(Xθ−y)
- 由上述推导得
Δ θ = 1 m X T e \Delta{\theta} = \cfrac{1}{m} X^{T} e Δθ=m1XTe
θ : = θ − α Δ θ = θ − α 1 m X T e \theta := \theta - \alpha \Delta{\theta} = \theta - \alpha \cfrac{1}{m} X^{T} e θ:=θ−αΔθ=θ−αm1XTe
Python实现
导包
import numpy as np
import matplotlib.pyplot as plt
数据预处理
x = np.array([4, 3, 3, 4, 2, 2, 0, 1, 2, 5, 1, 2, 5, 1, 3])
y = np.array([8, 6, 6, 7, 4, 4, 2, 4, 5, 9, 3, 4, 8, 3, 6])m = len(x)x = np.c_[np.ones([m, 1]), x]
y = y.reshape(m, 1)
theta = np.zeros([2, 1])
迭代过程
alpha = 0.01
iter_cnt = 1000 # 迭代次数
cost = np.zeros([iter_cnt]) # 代价数据for i in range(iter_cnt):h = x.dot(theta) # 估计值error = h - y # 误差值cost[i] = 1 / (2 * m) * error.T.dot(error) # 代价值# 更新参数delta_theta = 1 / m * x.T.dot(error)theta -= alpha * delta_theta
数据可视化
# 回归结果
plt.scatter(x[:, 1], y, c='blue')
plt.plot(x[:, 1], h, 'r-')
plt.show()# 代价结果
plt.plot(cost)
plt.show()
完整代码
import numpy as np
import matplotlib.pyplot as pltx = np.array([4, 3, 3, 4, 2, 2, 0, 1, 2, 5, 1, 2, 5, 1, 3])
y = np.array([8, 6, 6, 7, 4, 4, 2, 4, 5, 9, 3, 4, 8, 3, 6])m = len(x)x = np.c_[np.ones([m, 1]), x]
y = y.reshape(m, 1)
theta = np.zeros([2, 1])alpha = 0.01
iter_cnt = 1000 # 迭代次数
cost = np.zeros([iter_cnt]) # 代价数据for i in range(iter_cnt):h = x.dot(theta) # 估计值error = h - y # 误差值cost[i] = 1 / (2 * m) * error.T.dot(error) # 代价值# 更新参数delta_theta = 1 / m * x.T.dot(error)theta -= alpha * delta_theta# 线性拟合结果
plt.scatter(x[:, 1], y, c='blue')
plt.plot(x[:, 1], h, 'r-')
plt.show()# 代价结果
plt.plot(cost)
plt.show()
线性拟合结果

代价结果

相关文章:

【机器学习】【线性回归】梯度下降
文章目录 [toc]数据集实际值估计值估计误差代价函数学习率参数更新Python实现导包数据预处理迭代过程数据可视化完整代码 线性拟合结果代价结果 个人主页:丷从心 系列专栏:机器学习 数据集 ( x ( i ) , y ( i ) ) , i 1 , 2 , ⋯ , m \left(x^{(i)} , …...
JMeter逻辑控制器之While控制器
JMeter逻辑控制器之While控制器 1. 背景2.目的3. 介绍4.While示例4.1 添加While控制器4.2 While控制器面板4.3 While控制器添加请求4.3 While控制器应用场景 1. 背景 存在一些使用场景,比如:某个请求必须等待上一个请求正确响应后才能开始执行。或者&…...

记录 Docker 外部访问的基本操作
目录 1. 启动 docker 时挂载本地目录2. 外部访问 docker 容器 (-p/-P)3. 无法连接 docker 内 SSH 解决方案 1. 启动 docker 时挂载本地目录 # 将本地 D:/SDK 目录 挂载到 容器里的 /mnt/host 目录中 # 注意:-v /d/SDK:/mnt/host/ 必须放到 IMAGE_ID 前面才行 # …...
:BannerMessagePreference)
【Android 13】使用Android Studio调试系统应用之Settings移植(六):BannerMessagePreference
文章目录 一、篇头二、系列文章2.1 Android 13 系列文章2.2 Android 9 系列文章2.3 Android 11 系列文章三、BannerMessagePreference的移植3.1 新的问题:找不到 R.dimen.settingslib_preferred_minimum_touch_target3.2 问题分析(一)3.2.1 资源定义的位置3.2.2 检查依赖3.2…...

Python 变量
打印输出内容 print(‘rumenle’) print(‘haode’) 缩进需要tab 注释将需要注释的部分开头用# 多行注释 1、用你也可以左键选中我们需要注释的代码,松开,按:Ctrl/,就完成相同效果注释 2、把要注释的内容放到三个引号对里面 …...

ComfyUI如何中文汉化
comfyui中文地址如下: https://github.com/AIGODLIKE/AIGODLIKE-ComfyUI-Translationhttps://github.com/AIGODLIKE/AIGODLIKE-ComfyUI-Translation如何安装? 1. git安装 进入项目目录下的custom_nodes目录下,然后进入控制台,运…...
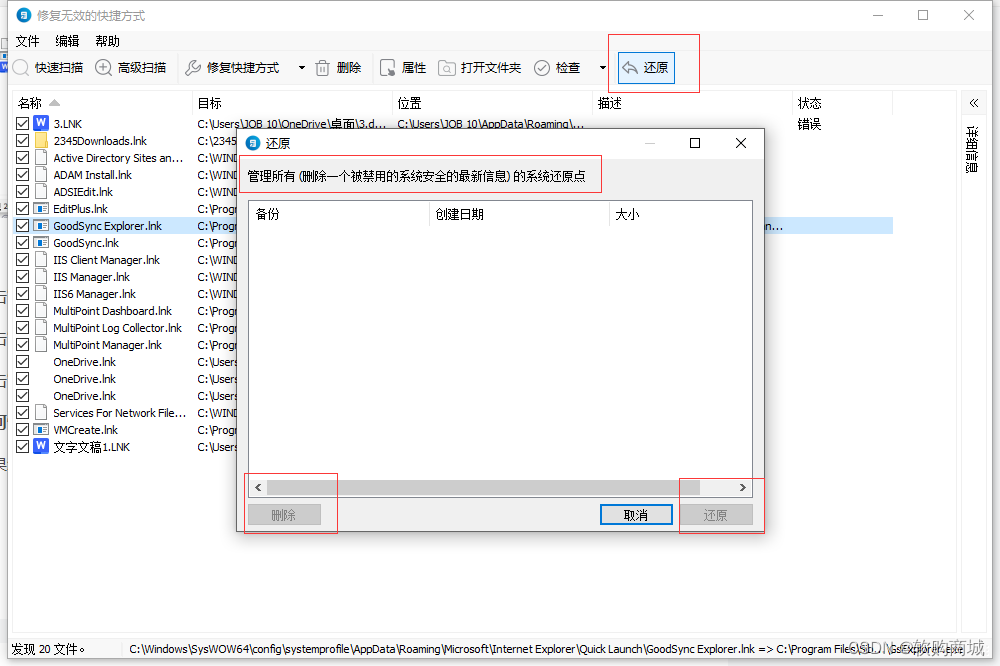
Glary Utilities Pro - 电脑系统优化全面指南:详尽使用教程
软件简介: Glary Utilities Pro 是一款全面的电脑优化工具,它旨在帮助用户提升计算机的性能和稳定性。这款软件提供了多种功能,包括系统清理、优化、修复以及保护。通过一键扫描,它可以识别并清除无用文件、临时数据、注册表错误等…...

1.4分页和排序
排序: -- 分页(limit)和排序(order by) -- 排序:升序ASC,降序DESC -- ORDER BY 通过字段排序,怎么排 -- 查询的结果根据成绩降序,升序 SELECT s.studentno,studentname,sub.subjectname,studentresult FROM student s RIGHT JO…...

Modbus转Profinet,不会编程也能用!轻松快上手!
Modbus转Profinet是一种用于工业自动化领域的通信协议转换器,可以将Modbus协议转换为Profinet协议,实现设备之间的数据交换与通信。这个工具的使用非常简单,即使没有编程经验的人也可以轻松上手。即使不会编程的人也可以轻松快速上手使用Modb…...
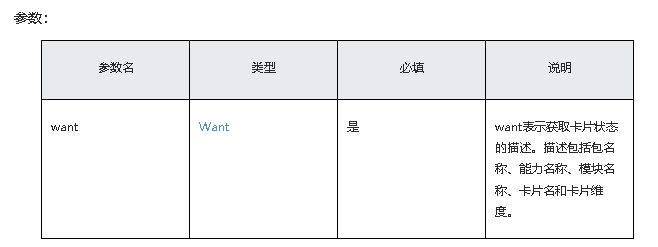
鸿蒙原生应用/元服务开发-Stage模型能力接口(十)下
ohos.app.form.FormExtensionAbility (FormExtensionAbility) 系统能力:SystemCapability.Ability.Form 示例 import FormExtensionAbility from ohos.app.form.FormExtensionAbility; import formBindingData from ohos.app.form.formBindingData; import formP…...

QT QPluginloader 加载失败,出现Unknown error 0x000000c1的问题
最近在学习Qt的插件开发,在加载插件时,一直失败,用如下代码加载并打印错误信息。 QDir dir("./testplugin.dll"); QPluginLoader pluginLoader(dir.absolutePath());//需要绝对路径 pluginLoader.load(); qDebug()<< "…...

众和策略:今年首次!A股罕见一幕
岁末,A股走出了不常见的行情。 这儿指的不单单是指数上涨。今天上午,A股逾3900只个股上涨,昨日逾4400只个股上涨,前天逾3700只个股上涨。据通达信数据显现,这种连续的普涨行情在本年还是头一次。 本年10月底…...
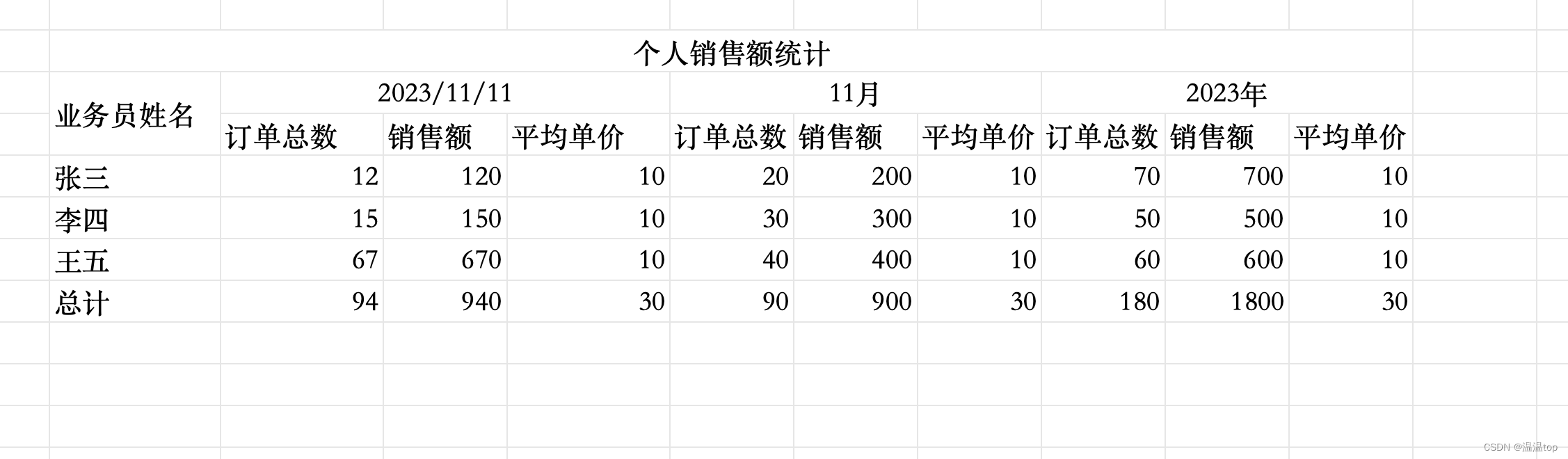
EasyExcel实现动态表头(注解实现)
要实现上述动态头,按每日统计,每月统计,每年统计。而时间是一直变化,所以我们需要表头也一直动态生成。 首先,我们需要定义所需要实体类 public class CountDayData {ExcelProperty(value "业务员姓名")p…...

什么是工厂方法模式,工厂方法模式解决了什么问题?
工厂方法模式是一种创建型设计模式,它定义了一个用于创建对象的接口,但将实际的实例化过程延迟到子类中。这样,客户端代码在不同的子类中实例化具体对象,而不是直接实例化具体类。工厂方法模式允许一个类的实例化延迟到其子类&…...
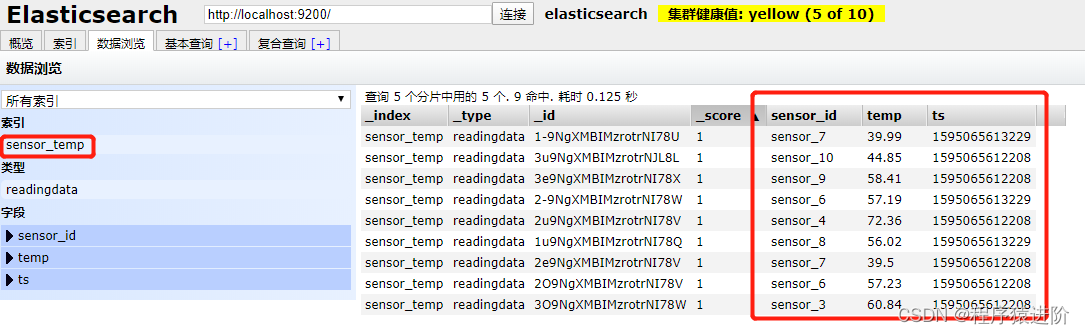
Flink 输出至 Elasticsearch
【1】引入pom.xml依赖 <dependency><groupId>org.apache.flink</groupId><artifactId>flink-connector-elasticsearch6_2.12</artifactId><version>1.10.0</version> </dependency>【2】ES6 Scala代码,自动导入的…...
web三层架构
目录 1.什么是三层架构 2.运用三层架构的目的 2.1规范代码 2.2解耦 2.3代码的复用和劳动成本的减少 3.各个层次的任务 3.1web层(表现层) 3.2service 层(业务逻辑层) 3.3dao 持久层(数据访问层) 4.结合mybatis简单实例演示 1.什么是三层架构 三层架构就是把…...

智能优化算法应用:基于厨师算法3D无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于厨师算法3D无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于厨师算法3D无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.厨师算法4.实验参数设定5.算法结果6.参考文献7.MA…...
写在2023年末,软件测试面试题总结
大家好,最近有不少小伙伴在后台留言,得准备年后面试了,又不知道从何下手!为了帮大家节约时间,特意准备了一份面试相关的资料,内容非常的全面,真的可以好好补一补,希望大家在都能拿到…...
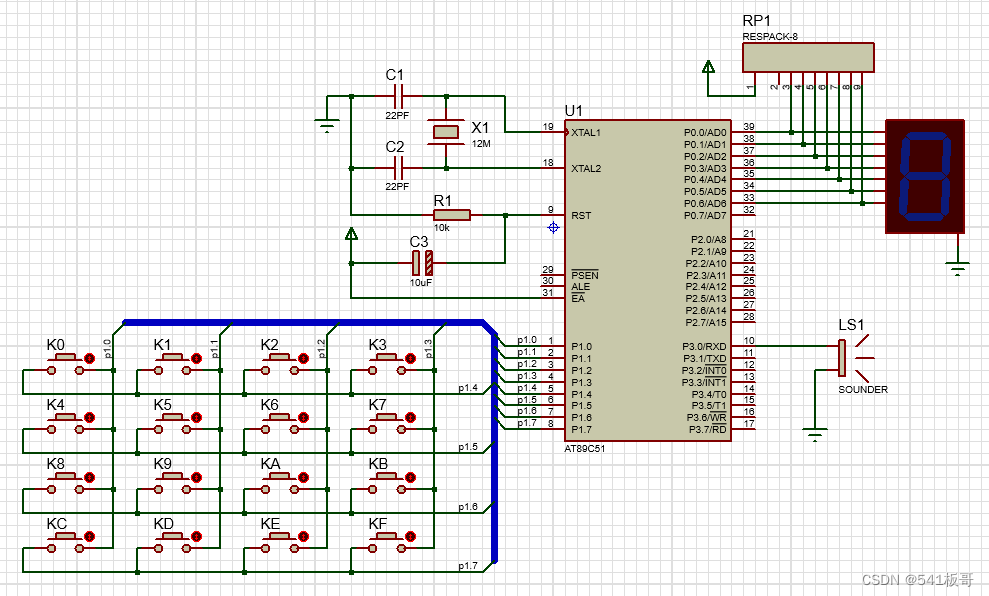
51系列--数码管显示的4X4矩阵键盘设计
本文介绍基于51单片机的4X4矩阵键盘数码管显示设计(完整Proteus仿真源文件及C代码见文末链接) 一、系统及功能介绍 本设计主控芯片选用51单片机,主要实现矩阵键盘对应按键键值在数码管上显示出来,矩阵键盘是4X4共计16位按键&…...
医院绩效考核系统源码,java源码,商业级医院绩效核算系统源码
医院绩效定义: “医院工作量绩效方案”是一套以工作量(RBRVS,相对价值比率)为核算基础,以工作岗位、技术含量、风险程度、服务数量等业绩为主要依据,以工作效率和效益、工作质量、患者满意度等指标为综合考…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...
