SVM(支持向量机)-机器学习
支持向量机(Support Vector Machine,SVM)是一种用于分类和回归分析的监督学习算法。它属于机器学习中的一类强大而灵活的模型,广泛应用于模式识别、图像分类、自然语言处理等领域。

基本原理:
SVM的基本原理是通过找到能够有效分隔不同类别的超平面来进行分类。在二维空间中,这个超平面就是一条直线,而在更高维空间中,它是一个超平面。SVM的目标是找到这个超平面,使得距离超平面最近的训练样本点(支持向量)到超平面的距离尽可能远,这个距离被称为间隔(margin)。
支持向量:
支持向量是指离超平面最近的那些训练样本点,它们对于定义超平面和间隔至关重要。在训练过程中,SVM主要关注这些支持向量,而其他样本点对于模型的影响较小。
核函数:
SVM可以通过核函数将输入空间映射到更高维的特征空间。这允许SVM在非线性问题上进行处理,通过将非线性问题转化为高维线性问题来解决。常用的核函数包括线性核、多项式核、径向基函数(Radial Basis Function,RBF)等。
核函数是支持向量机(SVM)中的一个重要概念,它用于将输入空间映射到更高维的特征空间。这个映射使得SVM在原始的输入空间中线性不可分的问题变得在高维特征空间中线性可分。核函数的引入是为了处理非线性问题,使得SVM能够更好地适应各种数据分布。
在SVM中,核函数的作用是计算两个样本之间的相似度或内积。通过核函数,我们可以在高维空间中隐式地表示数据点,而无需显式计算数据点在高维空间中的坐标。这种技巧被称为"核技巧"(kernel trick)。
常用的核函数有几种类型:
-
线性核函数(Linear Kernel):
K ( x , y ) = x T y K(x, y) = x^Ty K(x,y)=xTy这是最简单的核函数,它表示在原始的输入空间中进行线性分类。
-
多项式核函数(Polynomial Kernel):
K ( x , y ) = ( x T y + c ) d K(x, y) = (x^Ty + c)^d K(x,y)=(xTy+c)d多项式核函数引入了多项式的概念,其中 d d d是多项式的次数, c c c是一个常数。它允许SVM在原始空间中处理多项式特征。
-
径向基函数(Radial Basis Function,RBF)或高斯核函数(Gaussian Kernel):
K ( x , y ) = e − ∣ ∣ x − y ∣ ∣ 2 2 σ 2 K(x, y) = e^{-\frac{||x-y||^2}{2\sigma^2}} K(x,y)=e−2σ2∣∣x−y∣∣2RBF核函数是最常用的核函数之一,它通过将数据映射到无穷维的特征空间,从而适应更为复杂的非线性关系。 σ \sigma σ是控制函数宽度的参数。
-
sigmoid核函数(Sigmoid Kernel):
K ( x , y ) = tanh ( α x T y + c ) K(x, y) = \tanh(\alpha x^Ty + c) K(x,y)=tanh(αxTy+c)Sigmoid核函数也是一种常见的核函数,它通过类似于神经网络的激活函数(双曲正切函数)来进行非线性映射。
选择合适的核函数通常依赖于具体问题的性质和数据的分布。在实践中,RBF核函数是默认选择,因为它在很多情况下表现良好。核函数的选择也可能受到调参的影响,因为核函数参数的不同取值可能导致模型性能的差异。
软间隔和硬间隔:
在实际应用中,数据可能不是线性可分的,或者存在噪音。为了处理这些情况,SVM引入了软间隔,允许一些样本点出现在间隔内。这就是软间隔支持向量机,相对于严格线性可分的硬间隔支持向量机。

应用:
SVM在许多领域都有广泛的应用,包括文本分类、图像识别、生物信息学、金融预测等。由于其强大的泛化性能和对高维数据的适应能力,SVM在实际问题中取得了很好的效果。
总体而言,SVM是一种强大而灵活的机器学习算法,特别适用于处理复杂的非线性问题。
Question:
Q1:能够画出多少条线对样本点进行区分?
答:线是有无数条可以画的,区别就在于效果好不好,每条线都可以叫做一个划分超平面。比如上面的绿线就不好,蓝线还凑合,红线看起来就比较好。我们所希望找到的这条效果最好的线就是具有 “最大间隔的划分超平面”。
Q2:为什么要叫作“超平面”呢?
答:因为样本的特征很可能是高维的,此时样本空间的划分就不是一条线了。
Q3:画线的标准是什么?什么才叫这条线的效果好?哪里好?
答:SVM 将会寻找可以区分两个类别并且能使间隔(margin)最大的划分超平面。比较好的划分超平面,样本局部扰动时对它的影响最小、产生的分类结果最鲁棒、对未见示例的泛化能力最强。
Q4:间隔(margin)是什么?
答:对于任意一个超平面,其两侧数据点都距离它有一个最小距离(垂直距离),这两个最小距离的和就是间隔。比如下图中两条虚线构成的带状区域就是 margin,虚线是由距离中央实线最近的两个点所确定出来的(也就是由支持向量决定)。但此时 margin 比较小,如果用第二种方式画,margin 明显变大也更接近我们的目标。
相关文章:

SVM(支持向量机)-机器学习
支持向量机(Support Vector Machine,SVM)是一种用于分类和回归分析的监督学习算法。它属于机器学习中的一类强大而灵活的模型,广泛应用于模式识别、图像分类、自然语言处理等领域。 基本原理: SVM的基本原理是通过找到能够有效分…...

解决生成的insert语句内有单引号的情况
背景 因为Mybatis-Plus的saveBatch()方法的批量插入其实也是循环插入,而不是真正的一个SqlSession完成的批插,效率很低。所以我们在写批量插入的时候是自己实现了一个工具类去生成批量插入的sql再去执行,但是会遇到有些文本里有单引号导致插…...

【Linux 程序】1. 程序构建
文章目录 【 1. 配置 】【 2. 编译 】makefile编写的要点makefile中的全局自变量CMake编译依赖的库g编译 【 3. 安装 】 一般源代码提供的程序安装需要通过配置、编译、安装三个步骤; 配置。检查当前环境是否满足要安装软件的依赖关系,以及设置程序安装所…...
GLTF 编辑器实现逼真3D动物毛发效果
在线工具推荐: 3D数字孪生场景编辑器 - GLTF/GLB材质纹理编辑器 - 3D模型在线转换 - Three.js AI自动纹理开发包 - YOLO 虚幻合成数据生成器 - 三维模型预览图生成器 - 3D模型语义搜索引擎 要实现逼真的3D动物毛发效果,可以采用以下技术和方法&…...

【Go语言入门:Go语言的方法,函数,接口】
文章目录 4.Go语言的方法,函数,接口4.1. 方法4.1.1. 指针接受者4.1.2. 值接收者和指针接收者有什么区别?4.1.3. 方法 4.2. 接口4.2.1. 接口定义 4.3. 函数4.3.1. 函数介绍 4.Go语言的方法,函数,接口 4.1. 方法 4.1.1…...
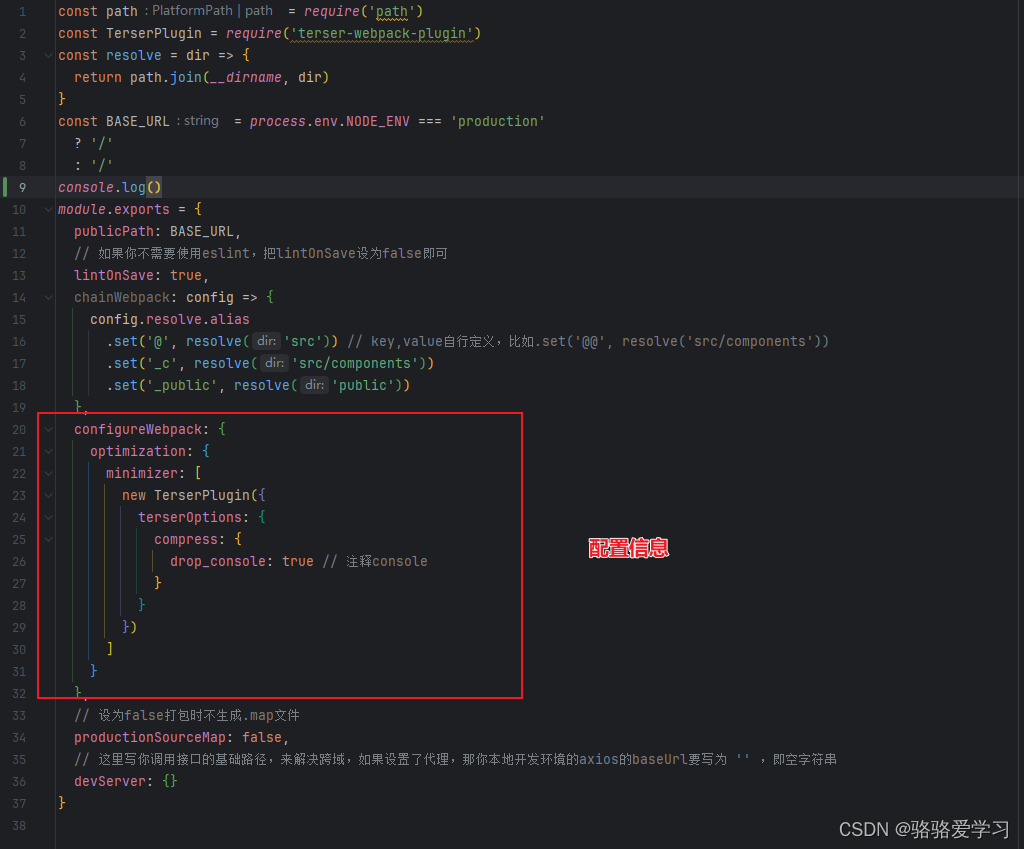
vue-cli3/webpack打包时去掉console.log调试信息
文章目录 前言一、terser-webpack-plugin是什么?二、使用配置vue-cli项目 前言 开发环境下,console.log调试信息,有助于我们找到错误,但在生产环境,不需要console.log打印调试信息,所以打包时需要将consol…...

企业品牌推广在国外媒体投放的意义和作用何在?
海外广告投放是企业在国际市场推广的重要战略,具有多种形式,包括社交媒体广告、短视频广告、电视广告等。这些广告形式在传播信息、推动销售、塑造品牌形象等方面发挥着独特的作用。 其中软文发稿是一种注重叙事和信息传递的广告形式,对于企…...
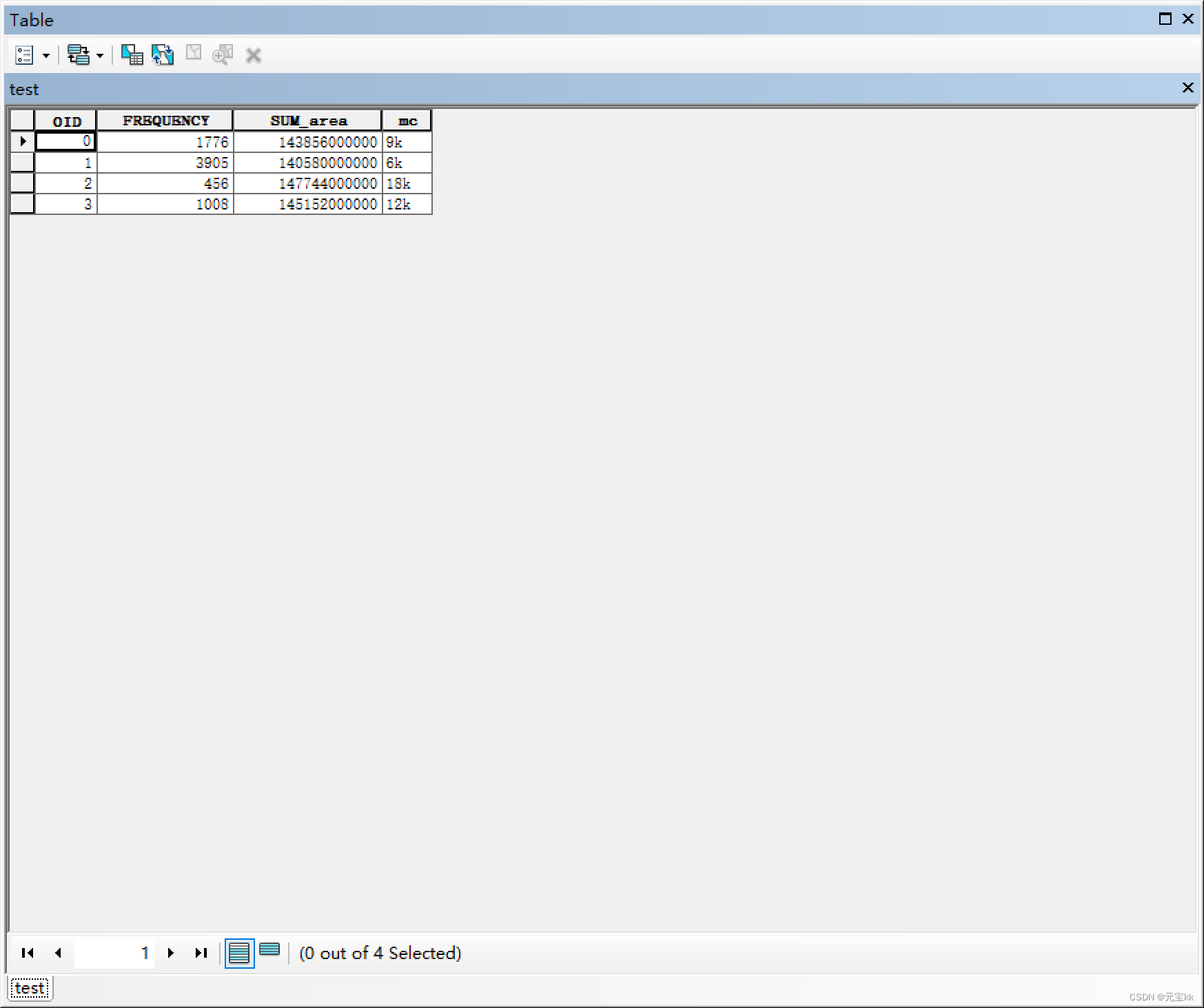
ArcGIS批量计算shp面积并导出shp数据总面积(建模法)
在处理shp数据时, 又是我们需要知道许多个shp字段的批量计算,例如计算shp的总面积、面积平均值等,但是单个查看shp文件的属性进行汇总过于繁琐,因此可以借助建模批处理来计算。 首先准备数据:一个含有多个shp的文件夹。…...
代码质量评价及设计原则
1.评价代码质量的标准 1.1 可维护性 可维护性强的代码指的是: 在不去破坏原有的代码设计以及不引入新的BUG的前提下,能够快速的修改或者新增代码. 不易维护的代码指的是: 在添加或者修改一些功能逻辑的时候,存在极大的引入新的BUG的风险,并且需要花费的时间也很长. 代码可…...

编程笔记 html5cssjs 012 HTML分块
编程笔记 html5&css&js 012 HTML分块 一、HTML 块级元素二、HTML 内联元素三、HTML <div> 元素四、HTML <span> 元素五、HTML<article>元素六、<article>元素和<div>元素的区别与联系小结 像报纸排版一样,很多时候需要把平面…...
【持续更新ing】uniapp+springboot实现个人备忘录系统【前后端分离】
目录 (1)项目可行性分析 (2)需求描述 (3)界面原型 (4)数据库设计 (5)后端工程 接下来我们使用uniappspringboot实现一个简单的前后端分离的小项目----个…...
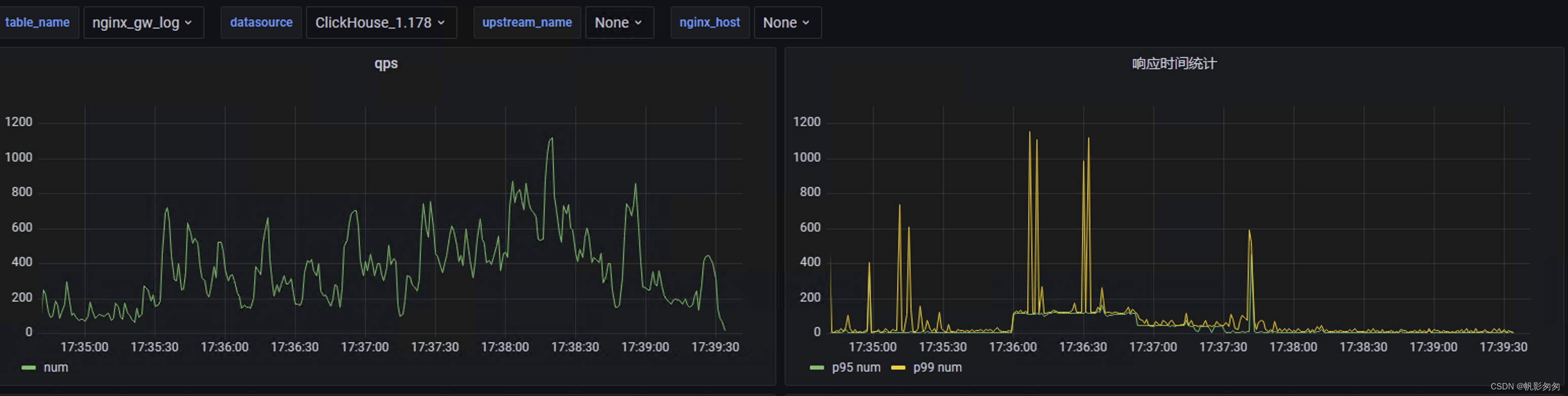
nginx+rsyslog+kafka+clickhouse+grafana 实现nginx 网关监控
需求 我想做一个类似腾讯云网关日志最终以仪表方式呈现,比如说qps、p99、p95的请求响应时间等等 流程图 数据流转就像标题 nginx ----> rsyslog ----> kafka —> clickhouse —> grafana 部署 kafka kafka 相关部署这里不做赘述,只要创…...

User maven 通过什么命令能查到那个包依赖了slf4j-simple-1.7.36.jar
要在 Maven 项目中查找哪个包依赖了 slf4j-simple-1.7.36.jar,您可以使用 Maven 的依赖树命令 mvn dependency:tree。这个命令会展示项目所有依赖的层次结构,包括传递依赖(即一个依赖的依赖)。然后,您可以搜索或过滤输…...

什么牌子冻干猫粮性价比高?性价比高的五款冻干猫粮牌子推荐
很多养猫的小伙伴们都磨刀霍霍准备给猫咪屯些猫冻干吧,特别是家里有挑食猫咪的家庭。有养猫的铲屎官们应该都知道,猫咪是对蛋白质的需求量很高,而且对植物蛋白的吸收效率比较低,所以蛋白质最好都是来自动物的优质蛋白。猫咪挑食就…...

扫描全能王启动鸿蒙原生应用开发,系HarmonyOS NEXT智能扫描领域首批
近期,“鸿蒙合作签约暨扫描全能王鸿蒙原生应用开发启动仪式”(简称“签约仪式”)正式举行。合合信息与华为达成鸿蒙合作,旗下扫描全能王将基于HarmonyOS NEXT正式启动鸿蒙原生应用开发。据悉,扫描全能王是鸿蒙在智能扫…...

[Angular] 笔记 8:list/detail 页面以及@Input
1. list 页面 list/detail 是重要的 UI 设计模式。 vscode terminal 运行如下命令生成 detail 组件: PS D:\Angular\my-app> ng generate component pokemon-base/pokemon-detail --modulepokemon-base/pokemon-base.module.ts CREATE src/app/pokemon-base/p…...
Zabbix“专家坐诊”第221期问答汇总
问题一 Q:使用官方docker模板Template App Docker,监控docker镜像,有一项监控项docker.data_usage有报错,不知道哪里问题:Cannot fetch data: Get “http://1.28/system/df”: context deadline exceeded (Client.Time…...
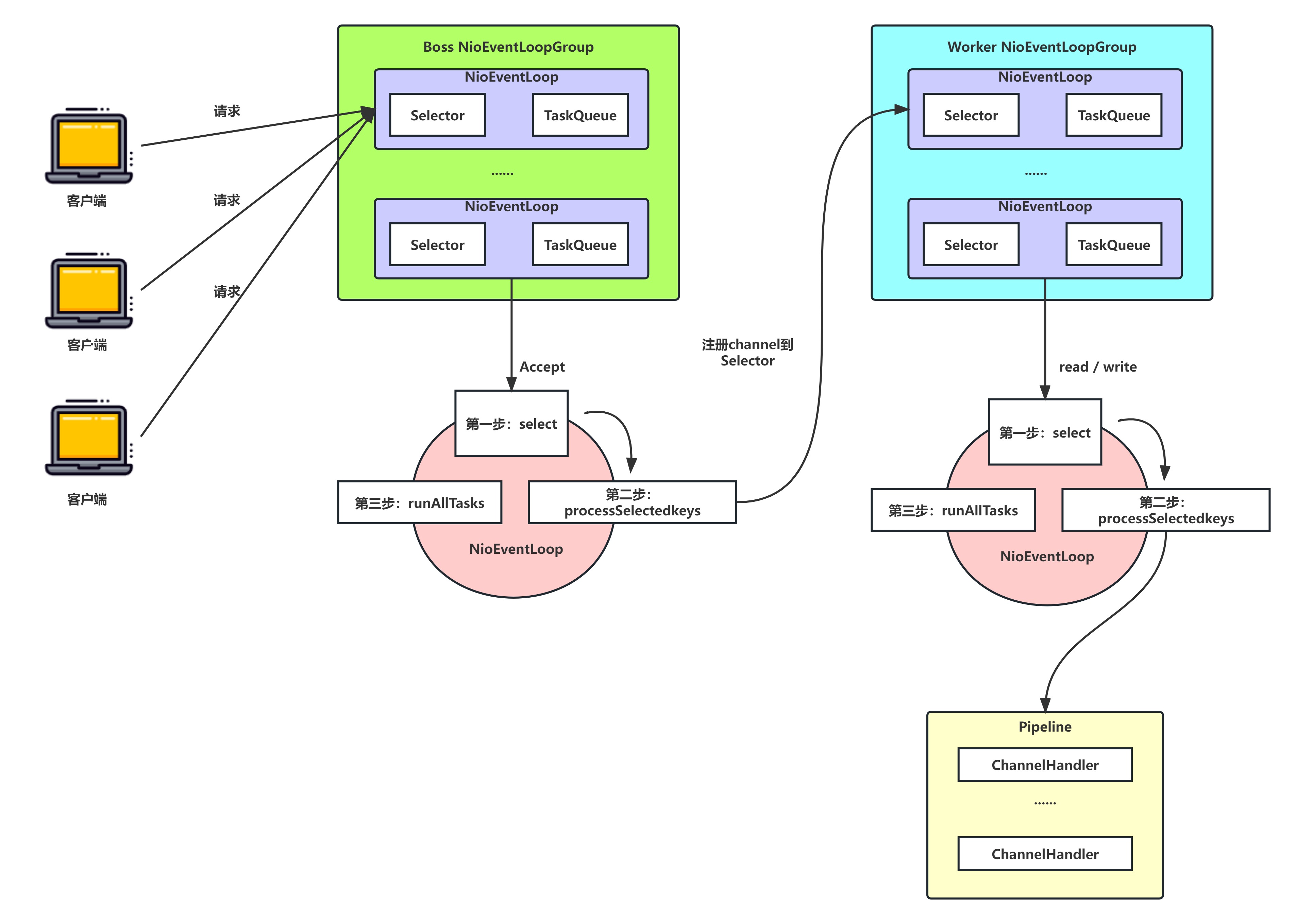
Netty—Reactor线程模型详解
文章目录 前言线程模型基本介绍线程模型分类Reactor线程模型介绍Netty线程模型: 传统阻塞IO的缺点Reactor线程模型单Reactor单线程模式单Reactor多线程模式主从Reactor多线程Reactor 模式小结 Netty 线程模型案例说明:Netty核心组件简介ChannelPipeline与…...

开源verilog模拟 iverilog verilator +gtkwave仿真及一点区别
开源的 iverilog verilator 和商业软件动不动几G几十G相比,体积小的几乎可以忽略不计。 两个都比较好用,各有优势。 iverilog兼容性好。 verilator速度快。 配上gtkwave 看波形,仿真工具基本就齐了。 说下基本用法 计数器 counter.v module…...
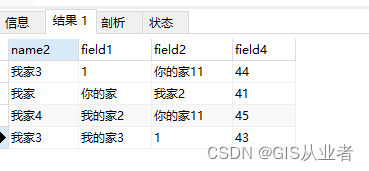
mysql中按字段1去重,按字段2降序排序
数据举例 sql语句 按字段field4降序排序,按字段field1去重 SELECT tt1.name2,tt1.field1,tt1.field2,tt1.field4 from ( select tt2.name2,tt2.field1,tt2.field2,tt2.field4 from t2 tt2 ORDER BY tt2.field4 DESC ) tt1 GROUP BY tt1.field1执行结果...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...

深入解析光敏传感技术:嵌入式仿真平台如何重塑电子工程教学
一、光敏传感技术的物理本质与系统级实现挑战 光敏电阻作为经典的光电传感器件,其工作原理根植于半导体材料的光电导效应。当入射光子能量超过材料带隙宽度时,价带电子受激发跃迁至导带,形成电子-空穴对,导致材料电导率显著提升。…...
