深度学习-【语义分割】学习笔记4 膨胀卷积(Dilated convolution)
文章目录
- 膨胀卷积
- 为什么需要膨胀卷积
- gridding effect
- 连续使用三次膨胀卷积——1
- 连续使用三次膨胀卷积——2
- 连续使用三次膨胀卷积——3
- Understanding Convolution for Semantic Segmentation
膨胀卷积
膨胀卷积,又叫空洞卷积。

左边是普通卷积,右边是膨胀卷积。
r 表示间隙,即膨胀因子。(当 r = 1时就是普通卷积)
一般使用过程中, 输入和输出特征图的高和宽是不会发生变化的。
复习:N = (W - F + 2P)/ S + 1
为什么需要膨胀卷积
在语义分割任务中,通常会使用分类网络作为backbone,在backbone中会对图片进行一系列的下采样。通过backbone之后,会使用一系列的上采样恢复原来的图片大小。如果特征图的高宽下采样倍率太大的话,还原到原来尺寸后,图片将丢失很多细节信息。
例如,在VGG网络中,通过max pooling层进行池化,这降低了特征图的高度和宽度,也丢失了一些细节信息,而丢失的信息无法通过上采样进行还原,在语义分割任务中将导致分割的效果不理想。而如果去掉max pooling层,将导致特征图的感受野变小。
利用膨胀卷积,既能增大感受野,又能保持输入输出特征图的高和宽不发生变化,解决了上述问题。但是,是否无脑堆叠膨胀卷积就可以了呢?
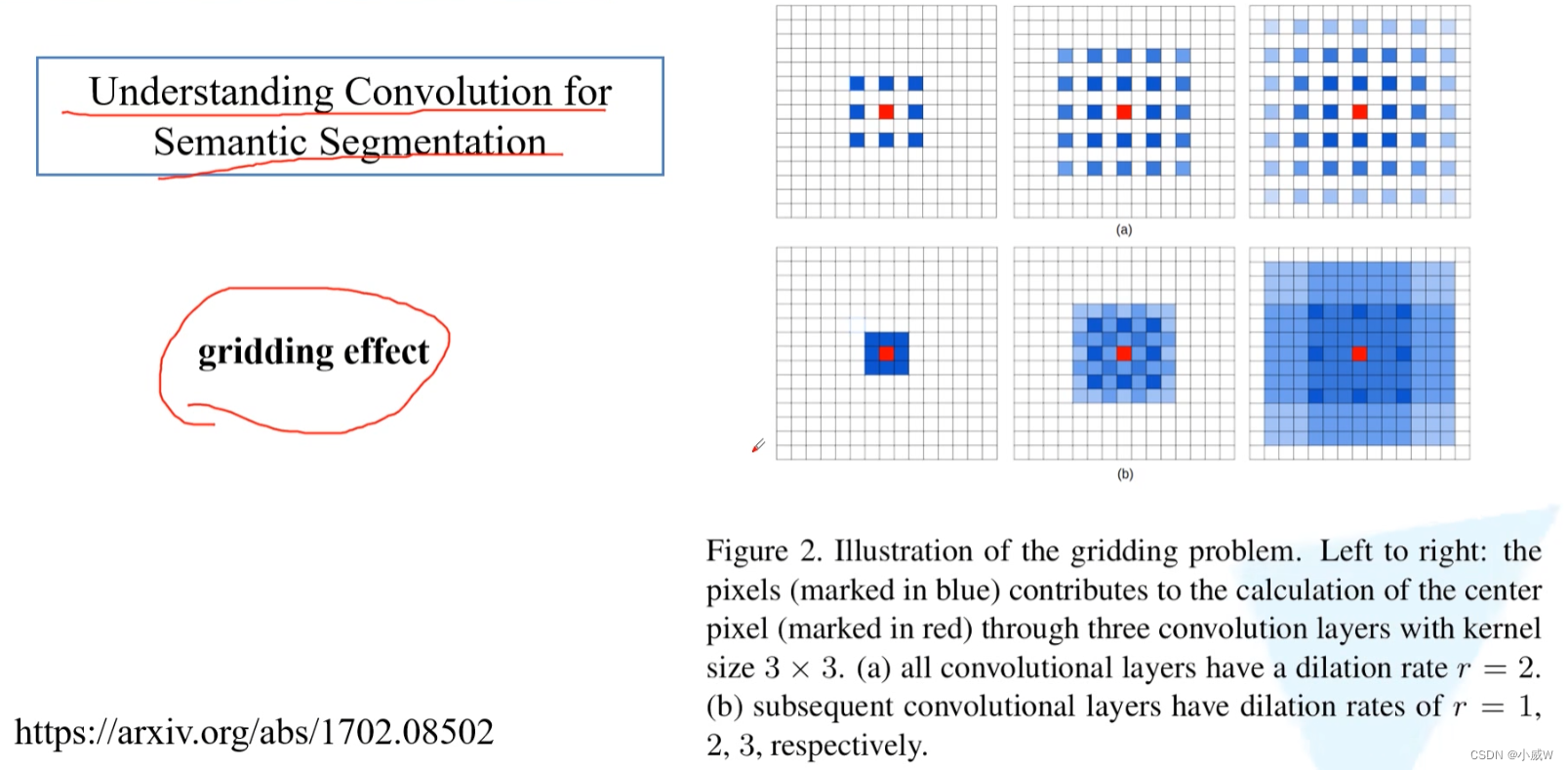
参考论文Understanding Convolution for Semantic Segmentation,在膨胀卷积使用过程中,会出现gridding effect的问题。
gridding effect
首先了解 什么是 gridding effect 问题:
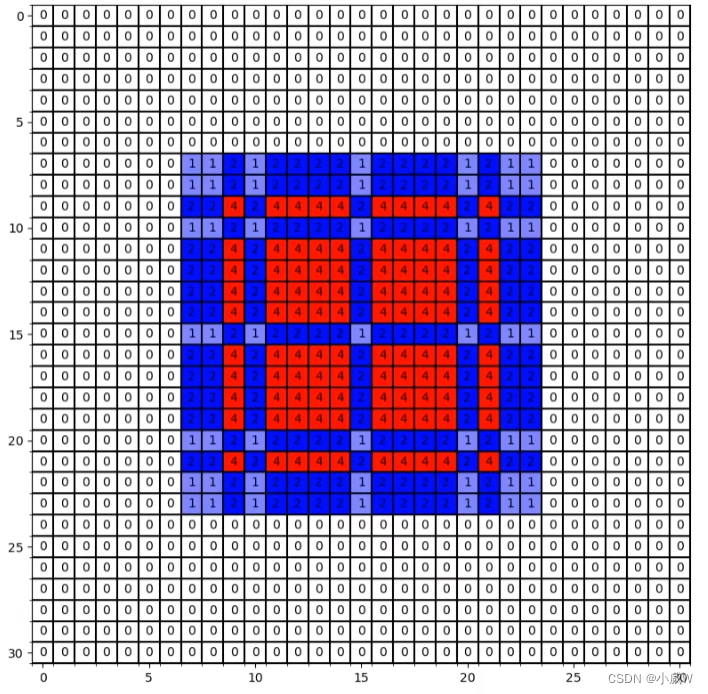
连续使用三次膨胀卷积——1
layer4上中心点使用各个点的信息的次数:
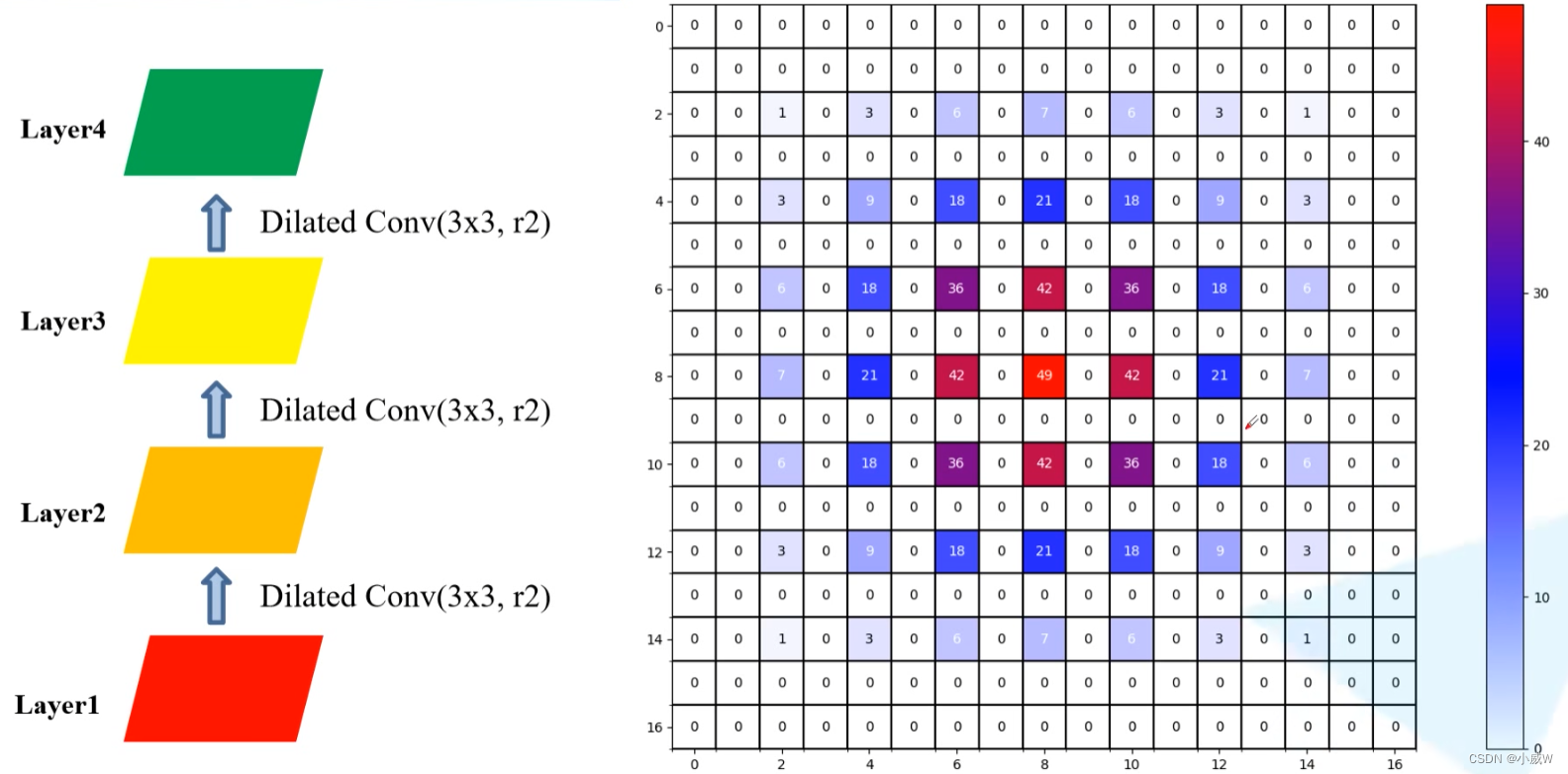
这就是gridding effect现象,即layer4上的一个像素并没有利用到这个范围内所有像素点的信息,而是有间隔的。(这就会导致一些细节上信息的丢失)。
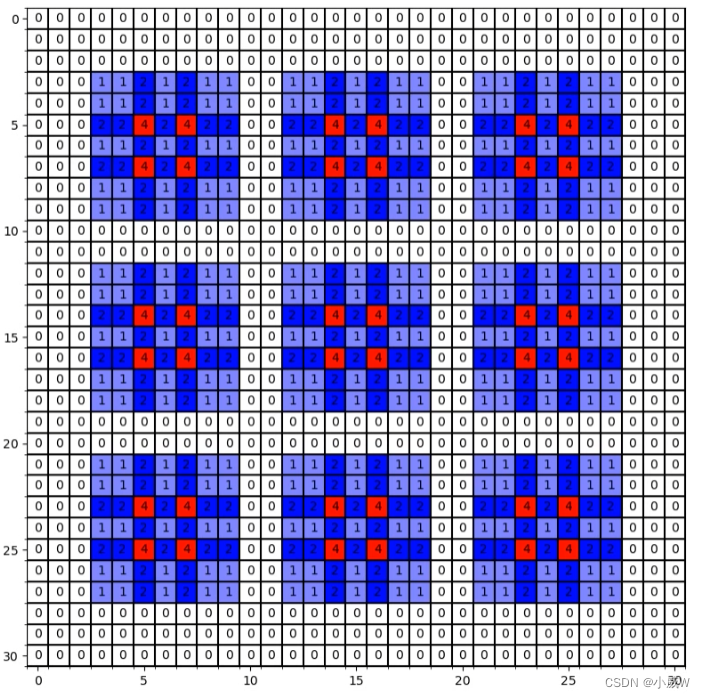
连续使用三次膨胀卷积——2
与实验一不同的是,第一个膨胀卷积的膨胀因子为1,也就是普通卷积。
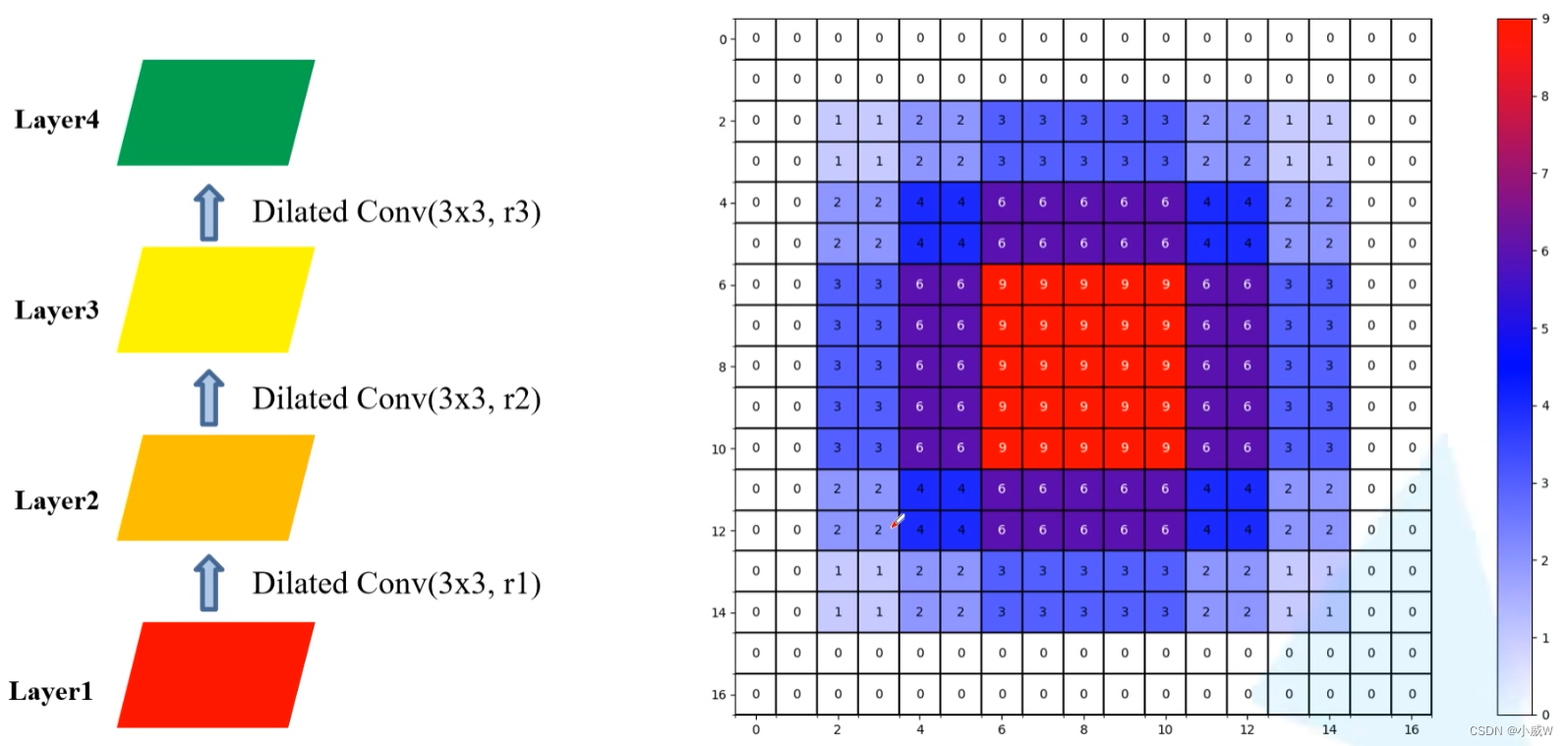
这里一个像素点使用的信息已经是某个范围内全部像素点的信息了。
感受野(RF,receptive field)= 13 × 13
连续使用三次膨胀卷积——3
连续使用三个普通卷积。
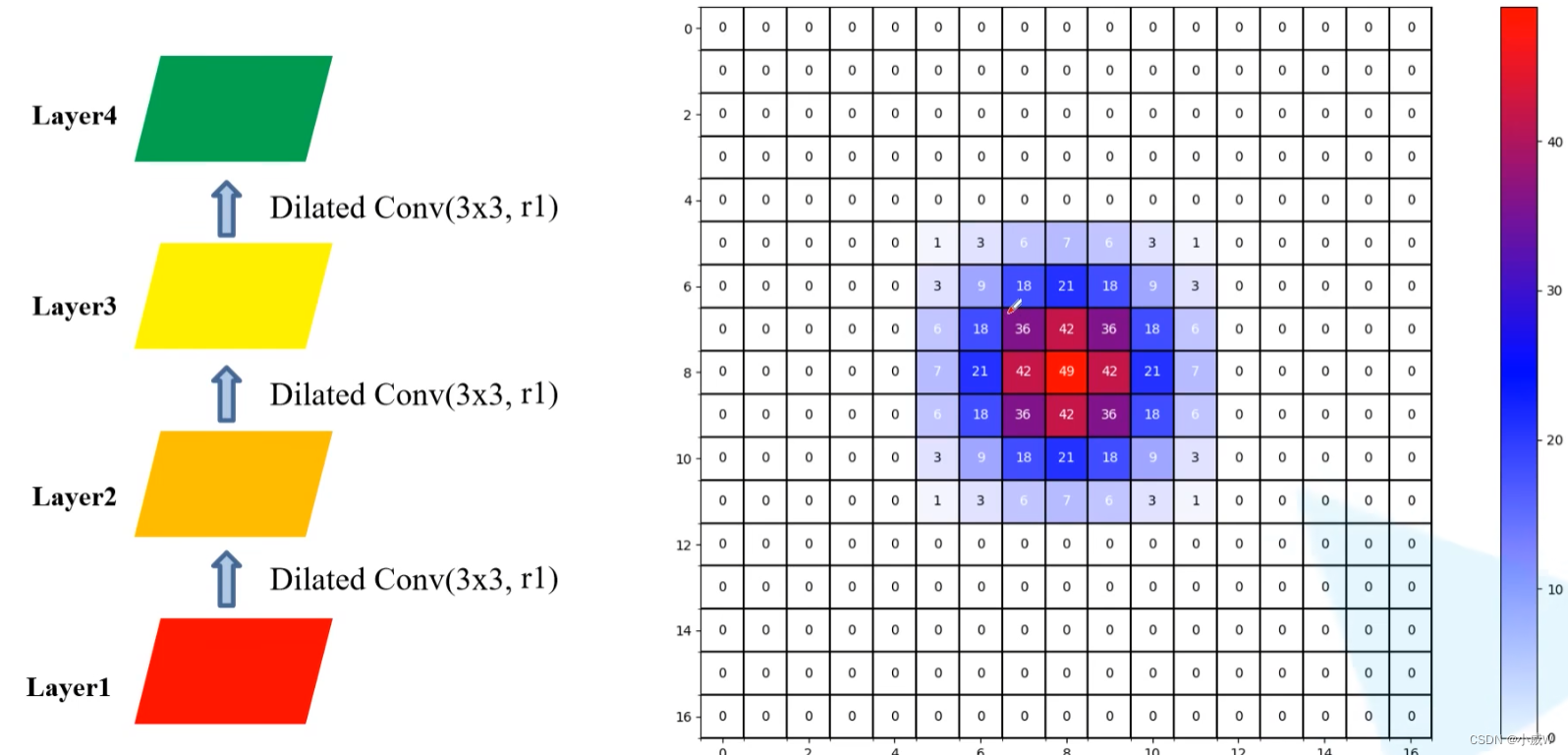
感受野(RF,receptive field)= 7 × 7
实验 2 和 3 对比,可以发现使用膨胀卷积在参数数量相同的情况下可以使感受野变大很多。
Understanding Convolution for Semantic Segmentation
@article{PanquWang2018UnderstandingCF, title={Understanding Convolution for Semantic Segmentation}, author={Panqu Wang and Pengfei Chen and Ye Yuan and Ding Liu and Zehua Huang and Xiaodi Hou and Garrison W. Cottrell}, journal={Workshop on Applications of Computer Vision}, year={2018}}
https://readpaper.com/paper/2592939477

Mi 表示第 i 层两个非零元素(即被使用到的像素)之间的最大距离。
设计原则1:需要 M2 <= K。
[1,2,5]
[1,2,9]

设计原则2:锯齿状膨胀因子设置,如[1,2,3,1,2,3]

设计原则3:公约数不能大于1
[2,4,8]
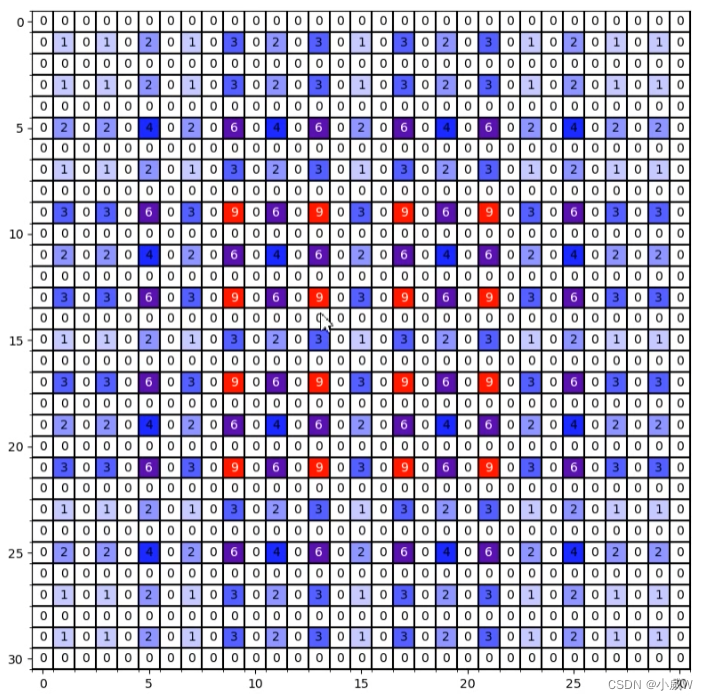
结果对比:
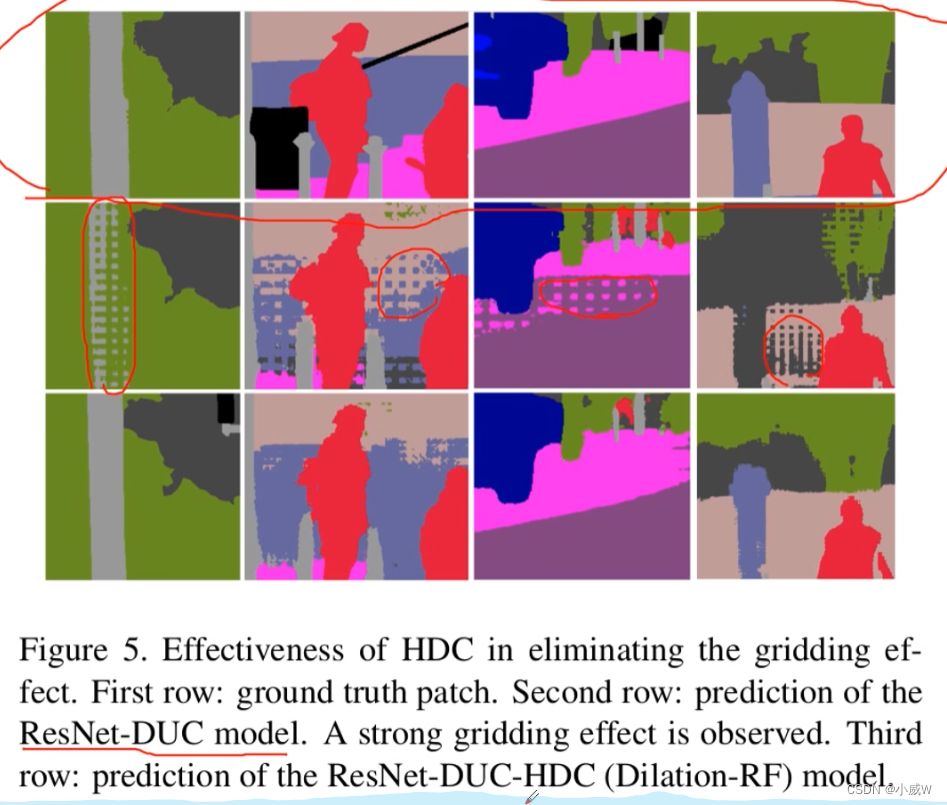
参考资料:
https://blog.csdn.net/Zen_of_code/article/details/127536998
https://www.bilibili.com/video/BV1Bf4y1g7j8/
相关文章:

深度学习-【语义分割】学习笔记4 膨胀卷积(Dilated convolution)
文章目录膨胀卷积为什么需要膨胀卷积gridding effect连续使用三次膨胀卷积——1连续使用三次膨胀卷积——2连续使用三次膨胀卷积——3Understanding Convolution for Semantic Segmentation膨胀卷积 膨胀卷积,又叫空洞卷积。 左边是普通卷积,右边是膨胀…...

【10】SCI易中期刊推荐——工程技术-计算机:人工智能(中科院2区)
🚀🚀🚀NEW!!!SCI易中期刊推荐栏目来啦 ~ 📚🍀 SCI即《科学引文索引》(Science Citation Index, SCI),是1961年由美国科学信息研究所(Institute for Scientific Information, ISI)创办的文献检索工具,创始人是美国著名情报专家尤金加菲尔德(Eugene Garfield…...
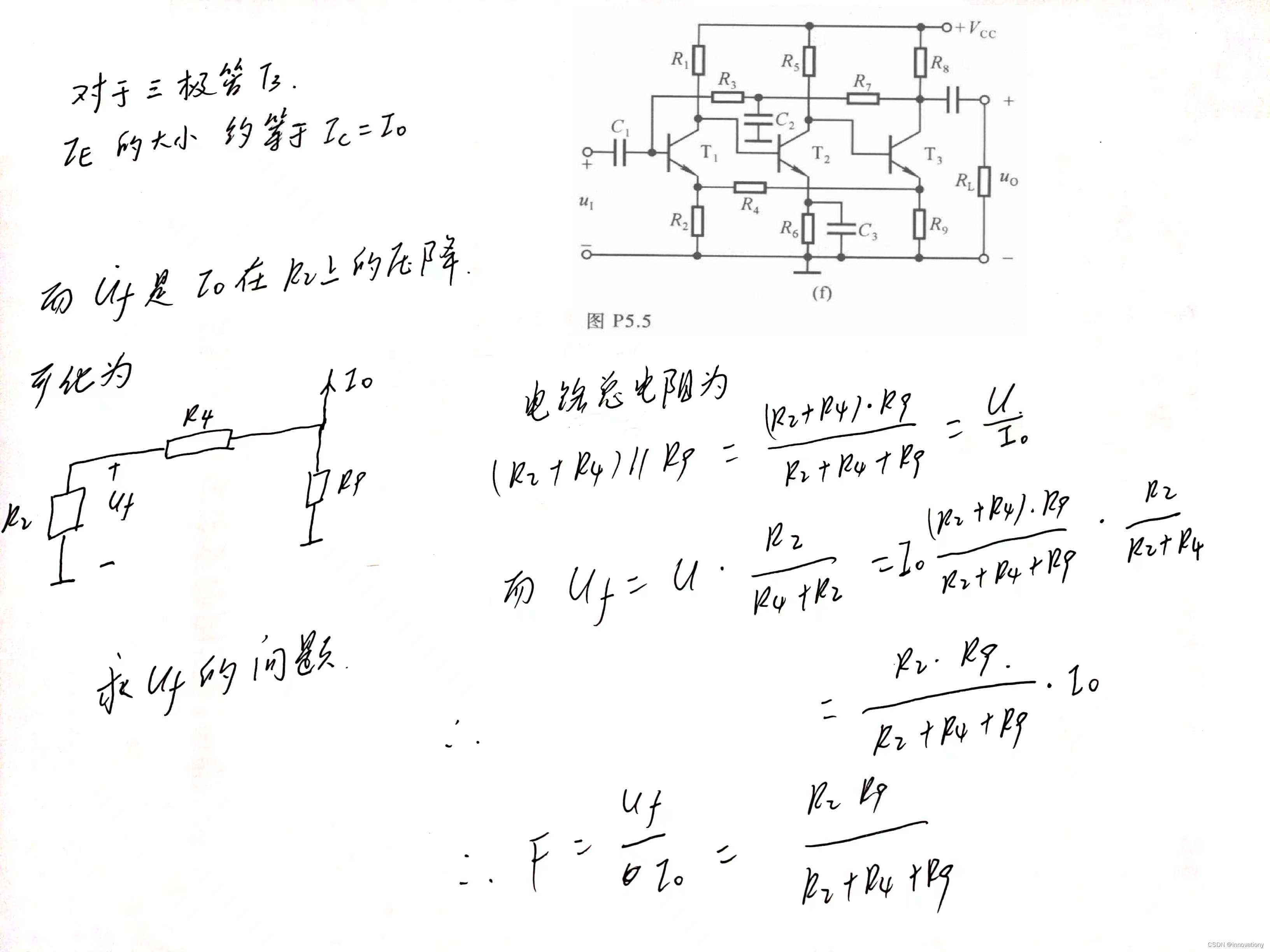
模电计算反馈系数,有时候转化为计算电阻分压的问题
模电计算反馈系数,有时候转化为计算电阻分压的问题 如果是电压反馈,F的除数是Uo 如果是电流反馈,F的除数是Io 串联反馈,F的分子是Uf 并联反馈,F的分子是If 点个赞呗,大家一起加油学习!...

专治Java底子差,不要再认为泛型就是一对尖括号了
文章目录一、泛型1.1 泛型概述1.2 集合泛型的使用1.2.1 未使用泛型1.2.2 使用泛型1.3 泛型类1.3.1 泛型类的使用1.2.2 泛型类的继承1.4 泛型方法1.5 泛型通配符1.5.1 通配符的使用1)参数列表带有泛型2)泛型通配符1.5.2 泛型上下边界1.6 泛型的擦除1.6.1 …...
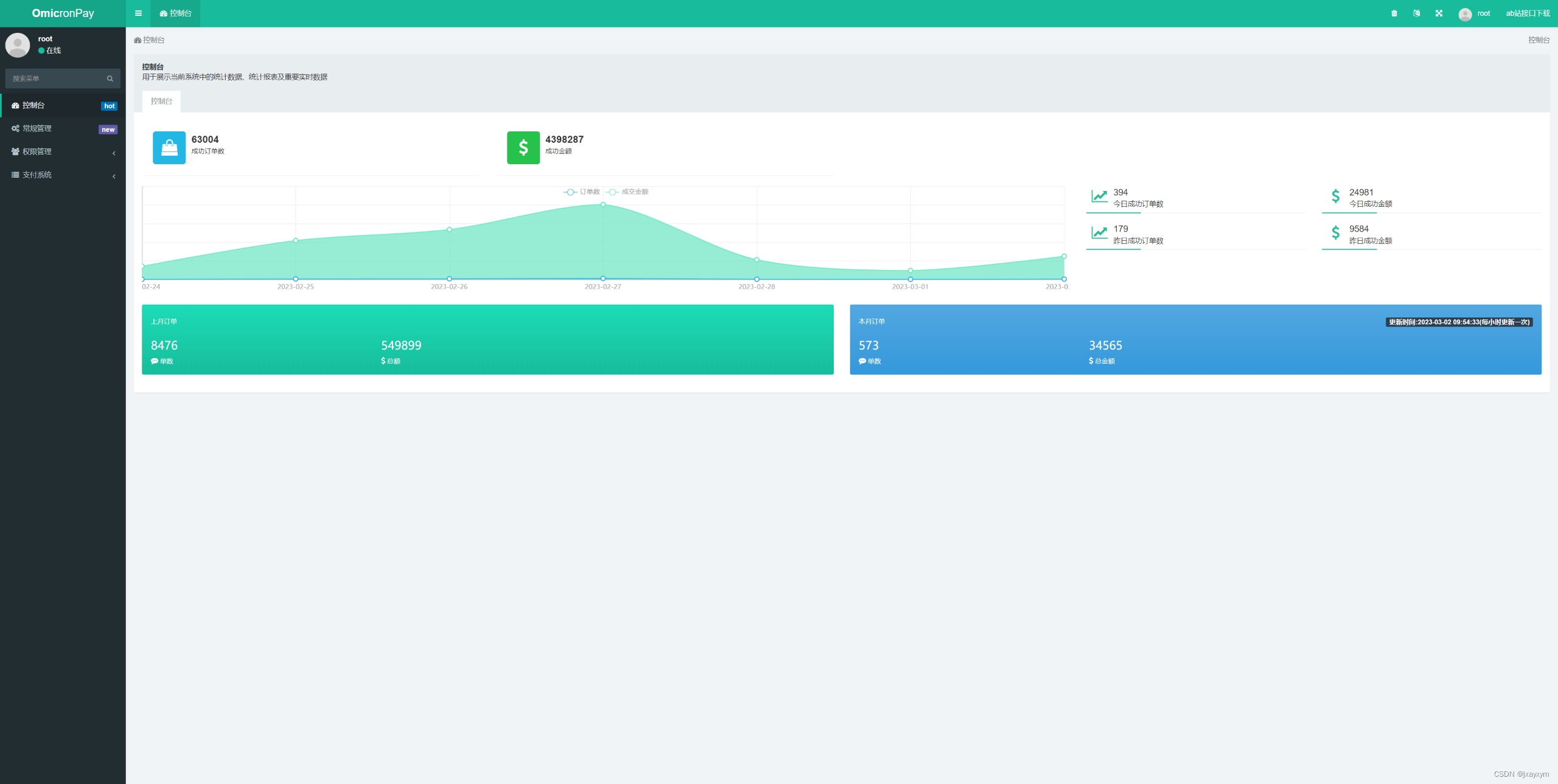
PayPal轮询收款的那些事儿
想必做跨境电商独立站的小伙伴,对于PayPal是再熟悉不过了,PayPal是一个跨国际贸易的支付平台,对于做独立站的朋友来说跨境收款绝大部分都是依赖PayPal以及Stripe条纹了。简单来说PayPal跟国内的支付宝有点类似,但是PayPal它是跨国…...
【Linux】项目自动化构建工具——make/Makefile
目录 1.make与Makefile的关系 Makefile make 项目清理 clean .PHONY 当我们编写一个较大的软件项目时,通常需要将多个源文件编译成可执行程序或库文件。为了简化这个过程,我们可以使用 make 工具和 Makefile 文件。Makefile 文件可以帮助我们自动…...

成本降低90%,OpenAI正式开放ChαtGΡΤ
今天凌晨,OpenAI官方发布ChαtGΡΤ和Whisper的接囗,开发人员现在可以通过API使用最新的文本生成和语音转文本功能。OpenAI称:通过一系列系统级优化,自去年12月以来,ChαtGΡΤ的成本降低了90%;现在OpenAI用…...

hls.js如何播放m3u8文件(实例)?
HLS(HTTP Live Streaming)是一种视频流传输协议,是苹果推出的适用于iOS与macOS平台的流媒体传输协议。它将视频分割成若干个小段,每个小段大小一般为2~10秒不等,并通过HTTP协议进行传输。通过在每个小段之间插入若干秒…...

大数据平台建设方法论集合
文章目录从0到1建设大数据解决方案大数据集群的方法论数据集成方法论机器学习算法平台方法论BI建设的方法论云原生大数据的方法论低代码数据中台的方法论大数据SRE运维方法论批流一体化建设的方法论数据治理的方法论湖仓一体化建设的方法论数据分析挖掘方法论数字化转型方法论数…...
25- 卷积神经网络(CNN)原理 (TensorFlow系列) (深度学习)
知识要点 卷积神经网络的几个主要结构: 卷积层(Convolutions): Valid :不填充,也就是最终大小为卷积后的大小. Same:输出大小与原图大小一致,那么N 变成了N2P. padding-零填充. 池化层(Subsampli…...

把数组里面数值排成最小的数
问题描述:输入一个正整数数组,将它们连接起来排成一个数,输出能排出的所有数字中最小的一个。例如输入数组{12, 567},则输出这两个能排成的最小数字12567。请给出解决问题的算法,并证明该算法。 思路:先将…...
云his系统源码 SaaS应用 基于Angular+Nginx+Java+Spring开发
云his系统源码 SaaS应用 功能易扩 统一对外接口管理 一、系统概述: 本套云HIS系统采用主流成熟技术开发,软件结构简洁、代码规范易阅读,SaaS应用,全浏览器访问前后端分离,多服务协同,服务可拆分ÿ…...

小红书场景营销怎么做?场景营销主要模式有哪些
小红书作为新兴媒体领域的佼佼者,凭借着生动,直观,代入感等元素的分享推荐收揽了巨额的流量。但是,随着时代的脚步逐渐加快,发展和变革随之涌来,传统的营销已经无法满足。所以场景营销就出现了。今天就来和…...

c++基础——数组
数组数组是存放相同类型对象的容器,数组中存放的对象没有名字,而是要通过其所在的位置访问。数组的大小是固定的,不能随意改变数组的长度。定义数组数组的声明形如 a[b],其中,a 是数组的名字,b 是数组中元素…...
odoo15 登录界面的标题自定义
odoo15 登录界面的标题自定义 原代码中查询:<title>Odoo<title> <html> <head><meta http-equiv="content-type" content="text/html; charset=utf-8" /><title>Odoo</title><link rel="shortcut icon…...

【内网服务通过跳板机和公网通信】花生壳内网穿透+Nginx内网转发+mqtt服务搭建
问题:服务不能暴露公网 客户的主机不能连外网,服务MQTT服务部署在内网。记做:p1 (computer 1)堡垒机(跳板机)可以连外网,内网IP 和 MQTT服务在同一个网段。记做:p2 (computer 2)对他人而言&…...

【多线程常见面试题】
谈谈 volatile关键字的用法? volatile能够保证内存可见性,强制从主内存中读取数据,此时如果有其他线程修改被volatile修饰的变量,可以第一时间读取到最新的值 Java多线程是如何实现数据共享的? JVM把内存分成了这几个区域: 方法区,堆区,栈区,程序计数器; 其中堆区…...

深度剖析指针(下)——“C”
各位CSDN的uu们你们好呀,今天小雅兰的内容还是我们的指针呀,上两篇博客我们基本上已经把知识点过了一遍,这篇博客就让小雅兰来带大家看一些和指针有关的题目吧,现在,就让我们进入指针的世界吧 复习: 数组和…...

爬虫与反爬虫技术简介
互联网的大数据时代的来临,网络爬虫也成了互联网中一个重要行业,它是一种自动获取网页数据信息的爬虫程序,是网站搜索引擎的重要组成部分。通过爬虫,可以获取自己想要的相关数据信息,让爬虫协助自己的工作,…...

Pag的2D渲染执行流程
Pag的渲染 背景 根据Pag文章里面说的,Pag之前长时间使用的Skia库作为底层渲染引擎。但由于Skia库体积过大,为了保证通用型(比如兼容CPU渲染)做了很多额外的事情。所以Pag的工程师们自己实现了一套2D图形框架替换掉Skiaÿ…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...
