小程序入门-登录+首页
正常新建一个登录页面
创建首页和TatBar，实现登录后底部出现两个按钮
代码
"pages": ["pages/login/index","pages/index/index","pages/logs/logs" ],"tabBar": {"list": [{"pagePath": "pages/index/index","text": "首页","iconPath": "res/images/tab/home.png","selectedIconPath": "res/images/tab/home-select.png"},{"pagePath": "pages/logs/logs", "text": "日志","iconPath": "res/images/tab/home.png","selectedIconPath": "res/images/tab/home-select.png"}]},把Login页面放在Page的第一个，这样程序进来默认就会打开登录页面。
登录成功后使用下面的方式跳转到首页
wx.switchTab({url: '../index/index'})如果想要在首页上面加一条灰色的线，可以在app全局样式里面添加下面代码
page::after{content: '';position: fixed;left: 0;bottom: 0;width: 100%;height: 1px;background-color: #E7E7E7;z-index: 9999;
}相关文章：
小程序入门-登录+首页
正常新建一个登录页面 创建首页和TatBar，实现登录后底部出现两个按钮 代码 "pages": ["pages/login/index","pages/index/index","pages/logs/logs" ],"tabBar": {"list": [{"pagePath"…...
React快速入门之组件
目录 组件JSX在标签使用{}嵌入JS表达式使用组件组件嵌套以🌲树的方式管理组件间的关系组件纯粹原则 组件 文件：Profile.js export default function Profile({isPacked true，head,stlyeTmp,src,size 80}) {if (isPacked) {head head &q…...
.NET Conf 2023 回顾 – 庆祝社区、创新和 .NET 8 的发布
作者： Jon Galloway - Principal Program Manager, .NET Community Team Mehul Harry - Product Marketing Manager, .NET, Azure Marketing 排版：Alan Wang .NET Conf 2023 是有史以来规模最大的 .NET 会议，来自全球各地的演讲者进行了 100 …...
Hadoop入门学习笔记——六、连接到Hive
视频课程地址：https://www.bilibili.com/video/BV1WY4y197g7 课程资料链接：https://pan.baidu.com/s/15KpnWeKpvExpKmOC8xjmtQ?pwd5ay8 Hadoop入门学习笔记（汇总） 目录 六、连接到Hive6.1. 使用Hive的Shell客户端6.2. 使用Beel…...
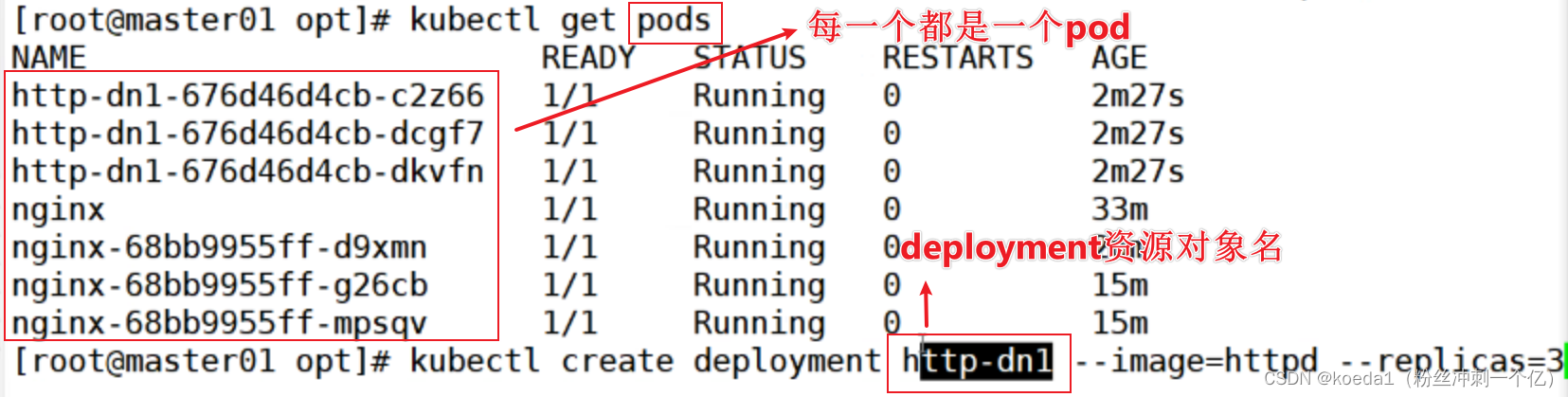
【K8S 基本概念】Kurbernetes的架构和核心概念
目录 一、Kurbernetes 1.1 简介 1.2、K8S的特性： 1.3、docker和K8S： 1.4、K8S的作用： 1.5、K8S的特性： 二、K8S集群架构与组件： 三、K8S的核心组件： 一、master组件： 1、kube-apiserve…...
WPS复选框里打对号，显示小太阳或粗黑圆圈的问题解决方法
问题描述 WPS是时下最流行的字处理软件之一，是目前唯一可以和微软office办公套件相抗衡的国产软件。然而，在使用WPS的过程中也会出现一些莫名其妙的错误，如利用WPS打开docx文件时，如果文件包含复选框，经常会出…...
对“企业数据资源相关会计处理暂行规定“的个人理解
附：2023年数据资源入表白皮书下载： 关注WX公众号： commindtech77， 获得数据资产相关白皮书下载地址 1. 回复关键字：数据资源入表白皮书 下载 《2023数据资源入表白皮书》 2. 回复关键字：光大银行 下载 光…...
JavaScript：函数隐含对象arguments/剩余参数. . .c/解构赋值
除了this，在函数内部还存在着一个隐含的参数arguments arguments 是一个类数组对象（伪数组） 调用函数时传递的所有实参，都被存储在arguments中 arguments[0] 表示的是第一个实参 arguments[1] 表示的是第二个实参 以此类推..…...
MFC窗体背景颜色的设置、控件白色背景问题、控件文本显示重叠问题、被父窗体背景覆盖的问题
文章目录 设置mfc窗体背景颜色窗体设置背景颜色后解决控件白色背景解决重复修改控件文本后重叠的问题自绘控件被父窗体背景覆盖的问题 设置mfc窗体背景颜色 设置窗体的背景颜色非常简单，只需要在窗体的OnEraseBkgnd里面填充窗体背景就可以了，甚至直接画…...
c++简易AI
今天小编一时雅兴大发，做了一个c的简易AI，还是很垃圾的！ 题外话（每期都会有）：我的蛋仔名叫酷影kuying，大家能加我好友吗？ 上代码咯！ #include<bits/stdc.h> #in…...
java获取两个List集合之间的交集、差集、并集
文章目录 方式一、jdk8 Stream求交集、并集、差集方式二、求交集方式三、collections4.CollectionUtils求交集、差集、并集 本文总结一下java中获取两个List之间的交集、补集、并集的几种方式。 最常用的通过for循环遍历两个集合的方式在这里就不整理了，主要整理一些…...
轻松实现iphone截图传电脑
目录 摘要 引言 用户登录工具和连接设备 生成截图 摘要 本篇博文介绍了克魔助手这款工具，解决了iPhone与Windows系统下图片传输的烦恼。通过连接同一Wi-Fi，使用克魔助手轻松实现了iPhone截图传输到电脑上的便捷操作。用户只需简单地下载并安装克魔助…...
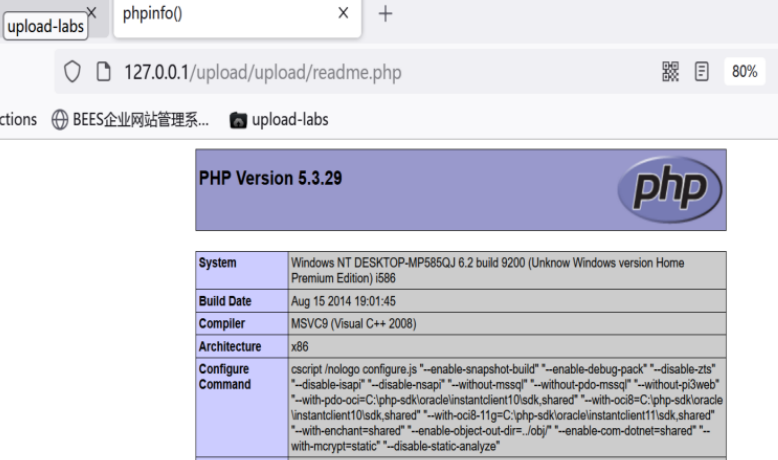
【网络安全】upload靶场pass1-10思路
目录 Pass-1 Pass-2 Pass-3 Pass-4 Pass-5 Pass-6 Pass-7 Pass-8 Pass-9 Pass-10 🌈嗨！我是Filotimo__🌈。很高兴与大家相识，希望我的博客能对你有所帮助。 💡本文由Filotimo__✍️原创，首发于CSDN…...
共享单车之数据存储
文章目录 第1关：获取工作簿中的数据第2关：保存共享单车数据 第1关：获取工作簿中的数据 相关知识 获取工作簿中的信息，我们可以使用Java POI（POI是一个提供API给Java程序对Microsoft Office格式档案读和写的功能&#…...
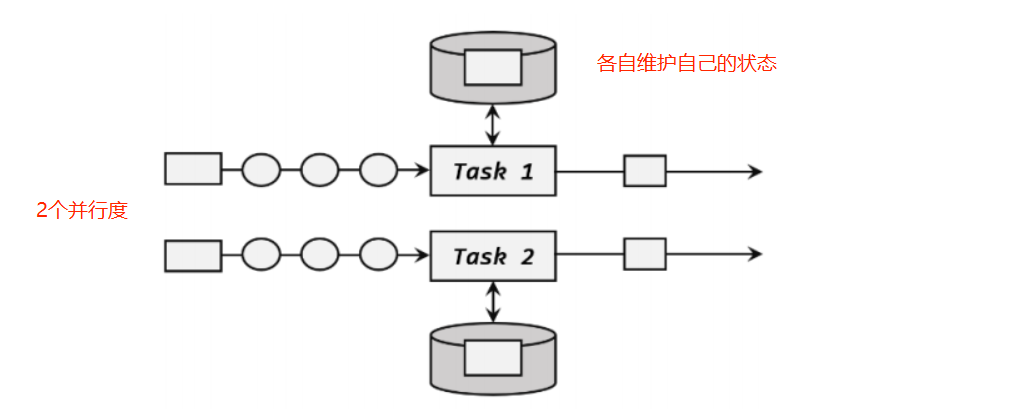
Flink（十一）【状态管理】
Flink 状态管理 我们一直称 Flink 为运行在数据流上的有状态计算框架和处理引擎。在之前的章节中也已经多次提到了“状态”（state），不论是简单聚合、窗口聚合，还是处理函数的应用，都会有状态的身影出现。状态就如同事务…...
【三维目标检测/自动驾驶】IA-BEV：基于结构先验和自增强学习的实例感知三维目标检测（AAAI 2024）
系列文章目录 论文：Instance-aware Multi-Camera 3D Object Detection with Structural Priors Mining and Self-Boosting Learning 地址：https://arxiv.org/pdf/2312.08004.pdf 来源：复旦大学 英特尔Shanghai Key Lab /美团 文章目录 系列文…...
wefew
123212...
Springboot整合JSP-修订版本(Springboot3.1.6+IDEA2022版本)
1、问题概述？ Springboot对Thymeleaf支持的要更好一些，Springboot内嵌的Tomcat默认是没有JSP引擎，不支持直接使用JSP模板引擎。这个时候我们需要自己配置使用。 2、Springboot整合使用JSP过程 现在很多的IDEA版本即使创建的项目类型是WAR工…...
Java核心知识点1-java和c++区别、隐式和显示类型转换
java和c区别 java通过虚拟机实现跨平台特性，但c依赖于特定的平台。java没有指针，它的引用可以理解为安全指针，而c和c一样具有指针。java支持自动垃圾回收，而c需要手动回收。java不支持多重继承，只能通过实现多个接口来…...
C++图论之强连通图
1. 连通性 什么是连通性？ 连通，字面而言，类似于自来水管道中的水流，如果水能从某一个地点畅通流到另一个地点，说明两点之间是连通的。也说明水管具有连通性，图中即如此。 无向图和有向图的连通概念稍有差…...
突破不可导策略的训练难题：零阶优化与强化学习的深度嵌合
强化学习（Reinforcement Learning, RL）是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程，然后使用强化学习的Actor-Critic机制（中文译作“知行互动”机制），逐步迭代求解…...
UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法：netstat [选项] 功能：查看网络状态 常用选项： n 拒绝显示别名&#…...
智能在线客服平台：数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展，消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁，不仅优化了客户体验，还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用，并…...
Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候，写过一篇简单实现，后期随着对该模型的深入研究，本次记录涉及到prophet 的公式以及参数调优，从公式可以更直观…...
srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935，SRS管理页面端口是8080，可…...
Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器，其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机（Virtual Host）。 1. 简介 Nginx 使用 server_name 指令来确定…...
k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN，根据VPN原理，打通两个内网必然需要借助一个公共中继节点，ktconnect工具巧妙的利用k8s原生的portforward能力，简化了建立连接的过程，apiserver间接起到了中继节…...
聊一聊接口测试的意义有哪些？
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开，首…...
Java 二维码
Java 二维码 **技术：**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...
C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性： 隐藏字段的实现细节 提供对字段的受控访问 访问控制： 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性： 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑： 可以…...