C++图论之强连通图
1. 连通性
什么是连通性?
连通,字面而言,类似于自来水管道中的水流,如果水能从某一个地点畅通流到另一个地点,说明两点之间是连通的。也说明水管具有连通性,图中即如此。
无向图和有向图的连通概念稍有差异。
无向图连通性
如果任意两点间存在路径,称此图具有连通性,如下的图结构具有连通性。提及连通性,就不得不说连通分量,通俗而言,指结构中有多少个连通通道,如下的图结构只有一个连通通道,也就是一个连通分量,所有节点在这个连通通道上都能互通。

而下图,则有2个连通分量。1,2,3,4,5可以在一个连通通道上互通,不能和6,7互通。6,7在自己的连通通道上可以互通。
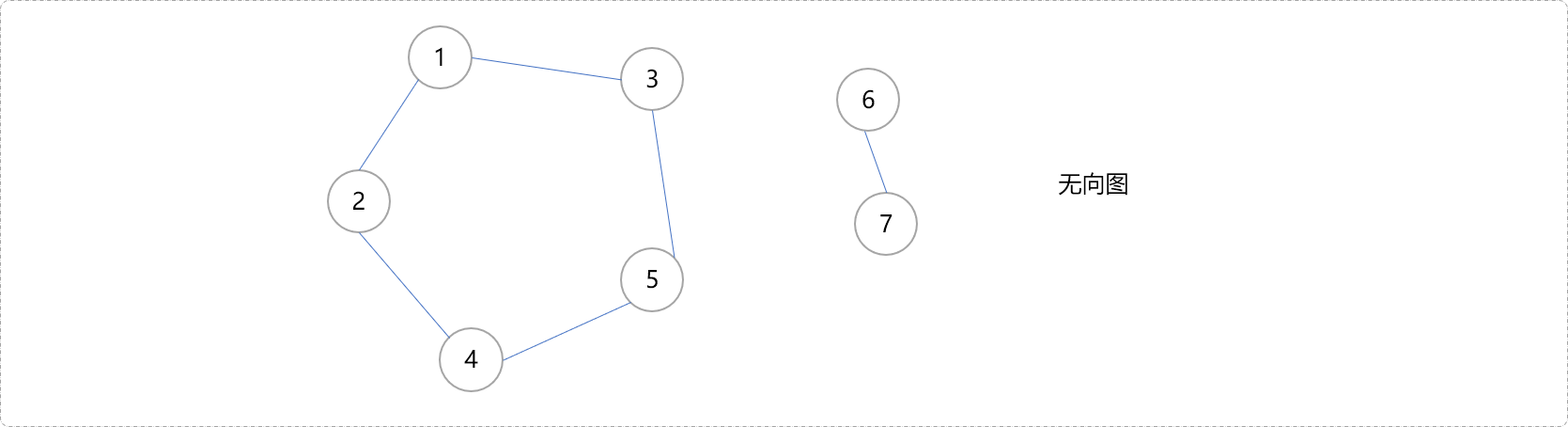
如何检查图结构的连通性和计算连通分量?
笨拙的方案自是使用深度或广度搜索算法。原理较简单,一次搜索完毕后,搜索到的节点必是在一个连通分量上。如果一次搜索完毕后被搜索出来的节点数量和图结构原有的节点数量相同,可证明只有一个连通分量。否则,可以再次从除第一次搜索出来的节点之外的节点开始重新搜索,再检查搜索出来的节点数量……如此如此,便可以检测出所有连通分量。
在性能要求不高的应用场景,这是不错的选择。否则,可以使用轻巧、快速的并查集数据结构来检查。
有向图的连通性
无论是在有向图或无向图中,都不可能改变连通这个概念。区别于有向图中的边有方向,无向图中的连通可以认为是双向通道,可认为是广义连通;有向图中的连通则是单向通道,可认为是狭义连通。
有向图中,如果一个节点能通过单向通道到达另一个节点,可认为这两点之间是连通的。如下图中,4->1、2->4->1是连通的,而2-3是不连通的。讨论连通的局部性没有太大意义,有向图中讨论的是强连通性。
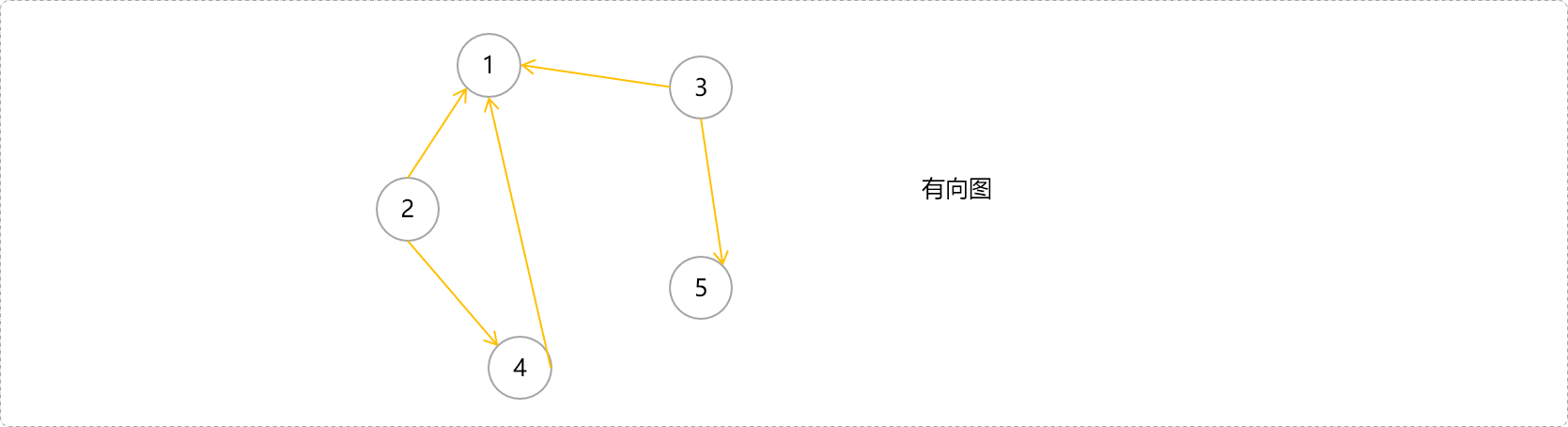
什么强连通?
强连通是有向图的特定概念。有向图中,任意两点之间都可以连通,则认定此有向图为强连通图,如下图。
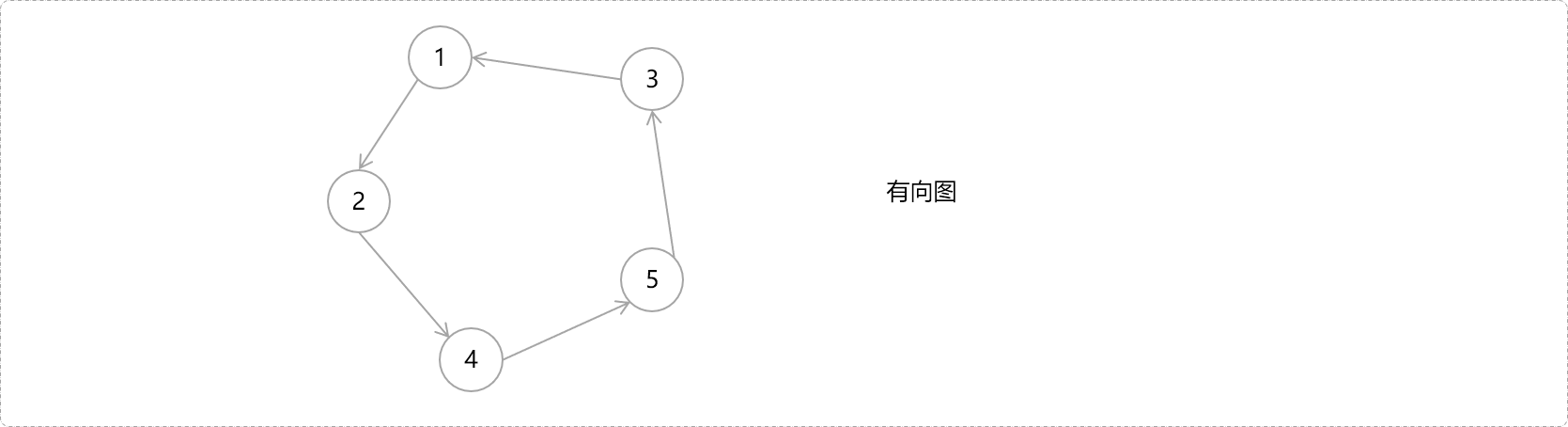
连通分量用来记录连通通道的数量,有向图中的连通分量指强连通分量。如上图,有一个强连通分量,也称此图为强连通性有向图。
如下图所示有向图结构,有向图本身不具有强连通性,但存在子图具有强连通性,则称子图即为原图的强连通分量。
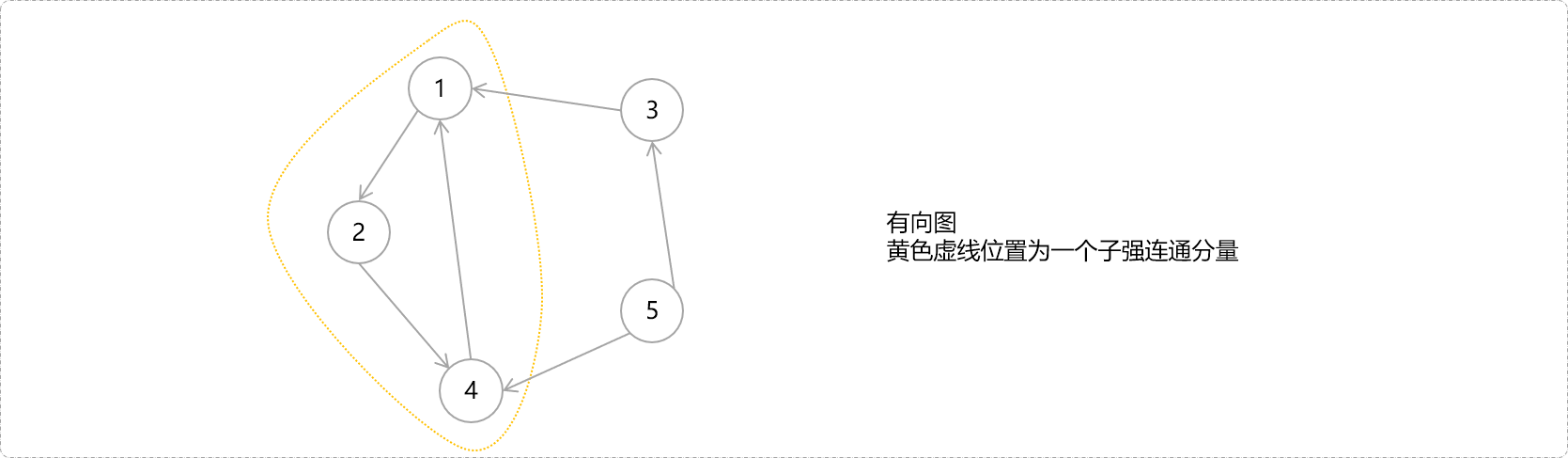
当然,具有强连通性的子图可能不只一个。猜一猜,下图有几个连通分量。
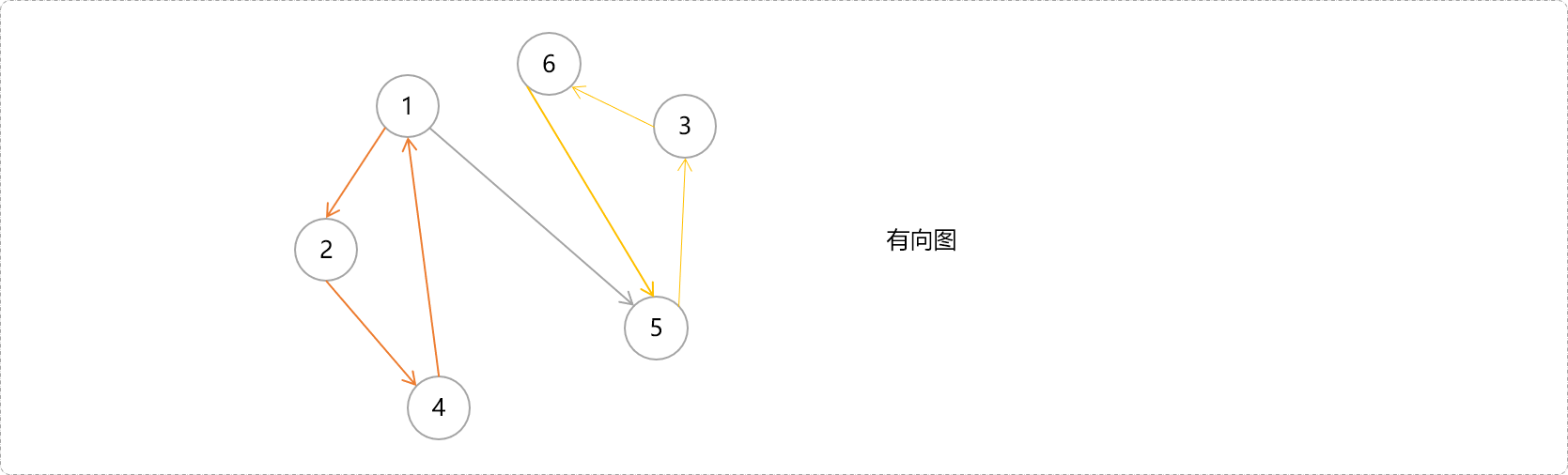
我们已知在无向图中计算连通分量的算法。那么在有向图中如何计算机强连通分量?
算法界有一句名言:没有暴力算法不能解决的问题。有向图中查找强连通子量,同样可以使用深度搜索或广度搜索。可以说,在树和图论问题中没有广度和深度搜索算法解决不了的。说起来感觉很历害,道理却是简单,任何问题都是在能搜索到的前提下得到解决的。
直接使用广度或深度搜索,毫无疑问属于暴力算法。虽然这是一条康庄大道,但是,不一定是一条捷径之路。好吧,现在让我们去发现是否有捷径小道。
2. Tarjan算法
Tarjan算法很优秀,也很优雅,颇有风淡云轻,四两拨千金之感。理解Tarjan算法,先要知晓几个概念,如DFS序、时间戳、回溯值……这些可以查阅我的文章《DFS序和欧拉序的降维打击》。
Tarjan可以解决很多问题。如公共祖先、割点、割边……当然还有本文的强连通分量的求解。
理解Tarjan算法求解强连通分量的工作机制之前,先搞明白有向图的 DFS 生成树中的 4 种边。

- 树边
(tree edge):节点与节点之间的边。 - 反祖边
(back edge):上图中以红色边表示(即7->1),也被叫做回边,即指向祖先节点的边。 - 横叉边
(cross edge):上图中以蓝色边表示(即9->7),搜索的时候遇到的一个已经访问过的结点,但是这个结点 并不是 当前结点的祖先。 - 前向边
(forward edge):上图中以绿色边表示(即3->6),在搜索的时候遇到子树中的结点的时候形成的。搜索过程所有前向边组成一条搜索分支。
DFS生成树与强连通分量之间的关系:
如果结点 u 是某个强连通分量在搜索树中遇到的第一个结点,那么这个强连通分量的其余结点肯定是在搜索树中以 u为根的子树中。结点 u被称为这个强连通分量的根。
以下图的结构为例,讲解查找强连通分量的流程。
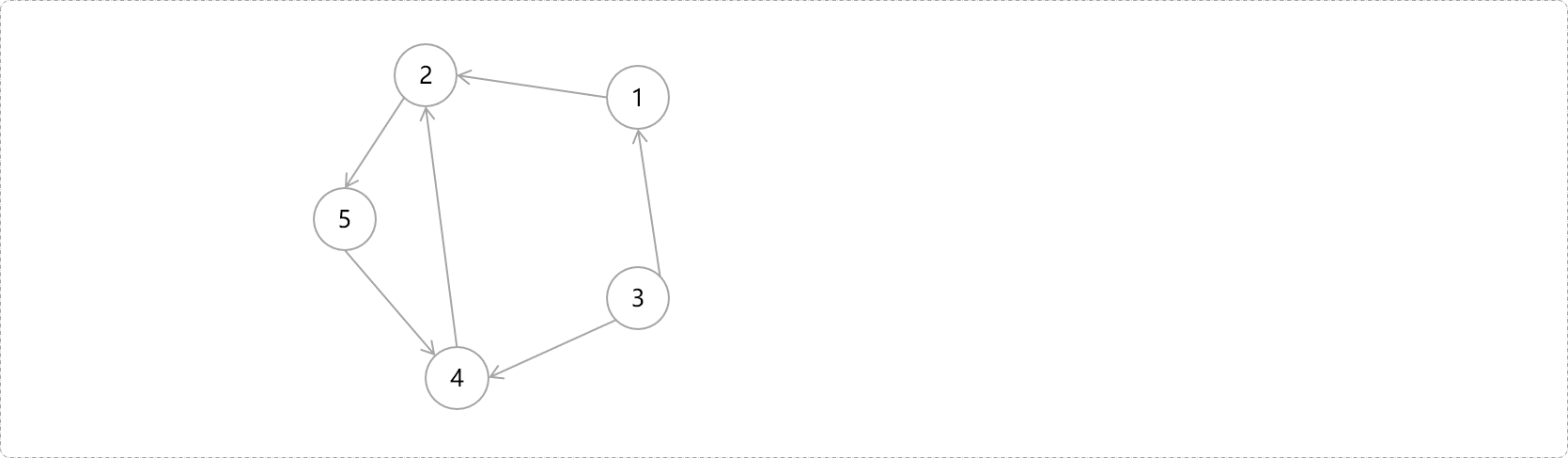
准备变量
- 栈
sta,存储强连通分量上的所有节点; dfn记录节点的时间戳,一个结点的子树内结点的dfn都大于该结点的dfn。也可以记录节点是否被访问过。low(回溯值)记录节点通过一条不在搜索树上的边能到达的结点。或者说不经过直接父节点能访问到的最早(远)的祖先,或者说是经过回边访问到的祖先节点。
搜索过程
- 从节点
1开始深度搜索,记录每一个节点在DFS时的时间戳以及回溯值。如1号节点的刚开始的时间戳为1,回溯值为1。别忘记了,1号节点现在也在栈中。
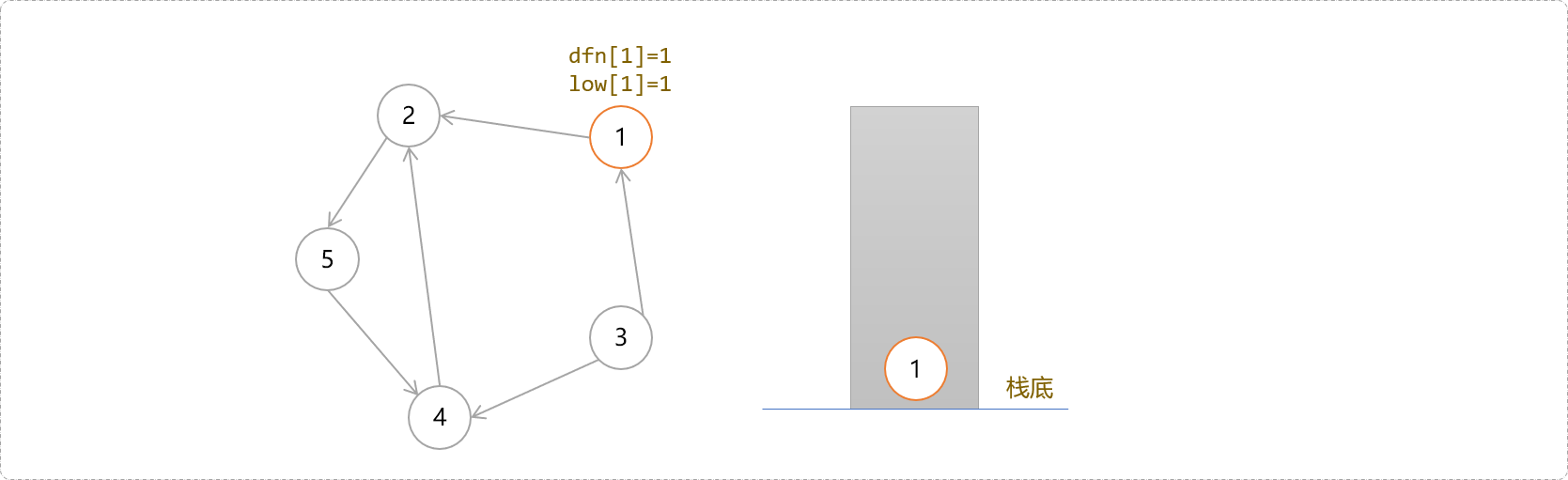
- 按深度搜索路线,一路下去,后面应该是
2、5、4。下图给出了当搜索到4号节点时,每一个节点的时间戳和回溯值以及栈中的状态。此时栈中由栈底到栈顶存储着一条DFS搜索树:1->2->5->4。
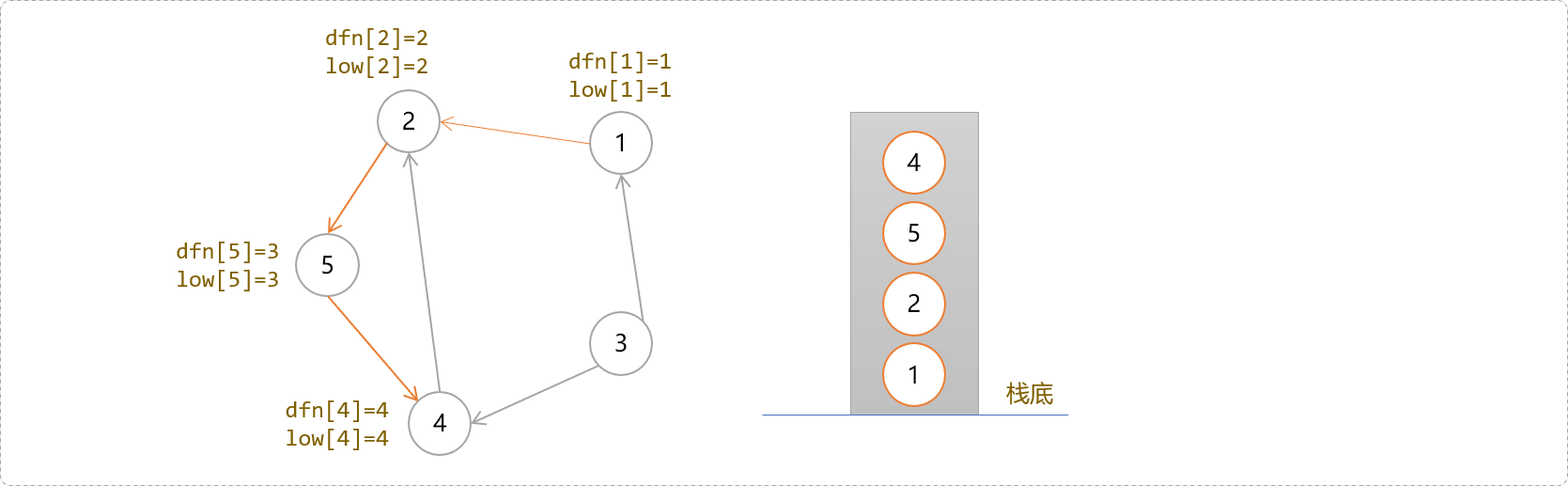
-
当从
4号节点访问到2号节点时,转机出现了。因为,2节点被访问过,现又以4号节点的子节点身份重新被访问,会想到是不是碰到了祖先,或者说遇到了同一个强连通分量上的节点?答案是,不能这么简单的认为?因为这种情况有可能是回边也有可能是横叉边。
如下图所示。
从
1号开始深度搜索,在第一条深度搜索分支结束后,4号节点也会被标记为被访问过。回溯到1号节点后,会开始第二条分支,在再次搜索到4号节点时,同样会发现4号节点也被访问。难道说4号节点和1号节点在同一个强连通分量上吗?4->2是回边,而1->4是横叉边。
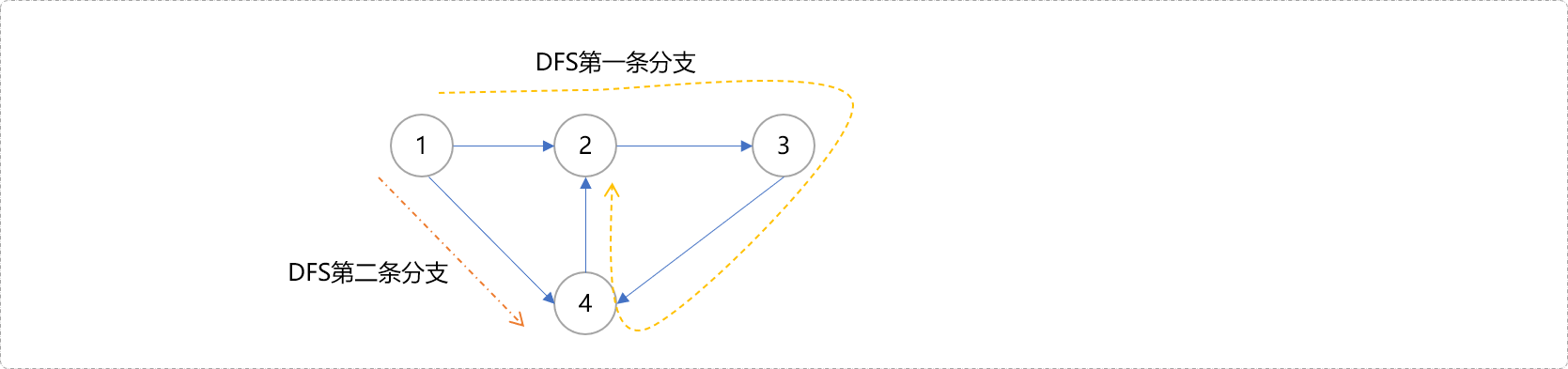
那么应该如何做出正确判断?继续回到我们的图结构上来讨论怎么正确得到强连通分量。
下图中2号节点在栈中,说明早于4号节点被访问到且还没有加入其它的强连通分量上,可以判断2是4号的祖先。所以节点是否在栈中,是判断是不是回边的一个很重要的条件。
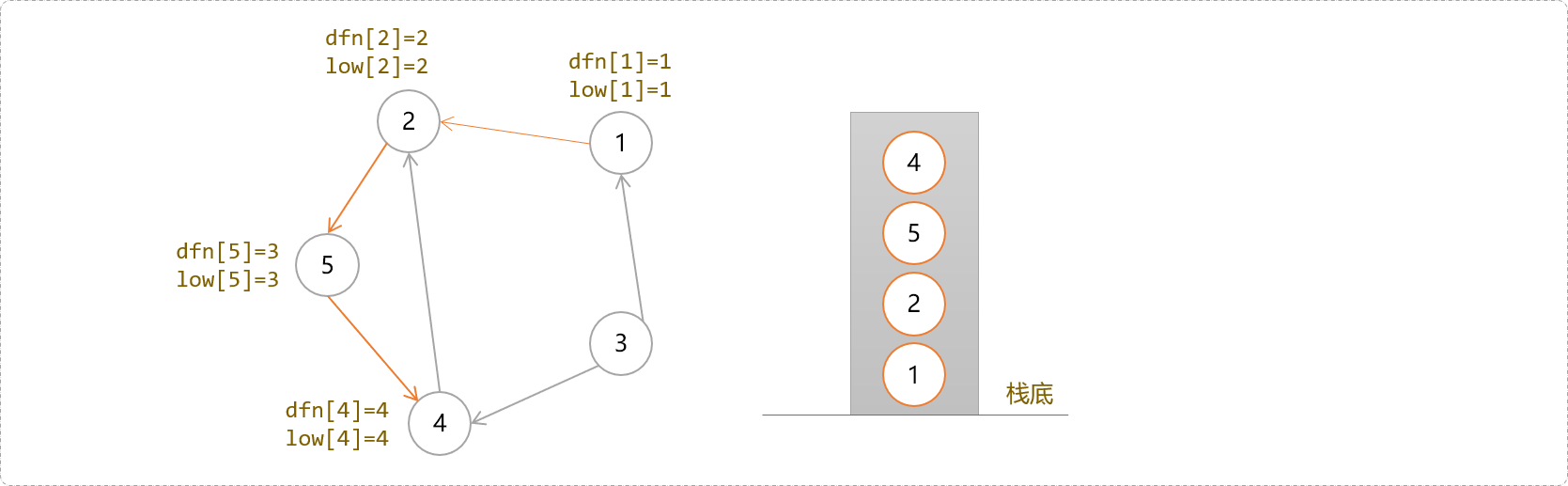
- 于是,更新
4号节点的low[4]=2。既然4号节点能到达2号节点,显然,点4的父节点们也能通过4号节点到达2号节点……一脉相承吗?于是这些节点的low值得以更新。
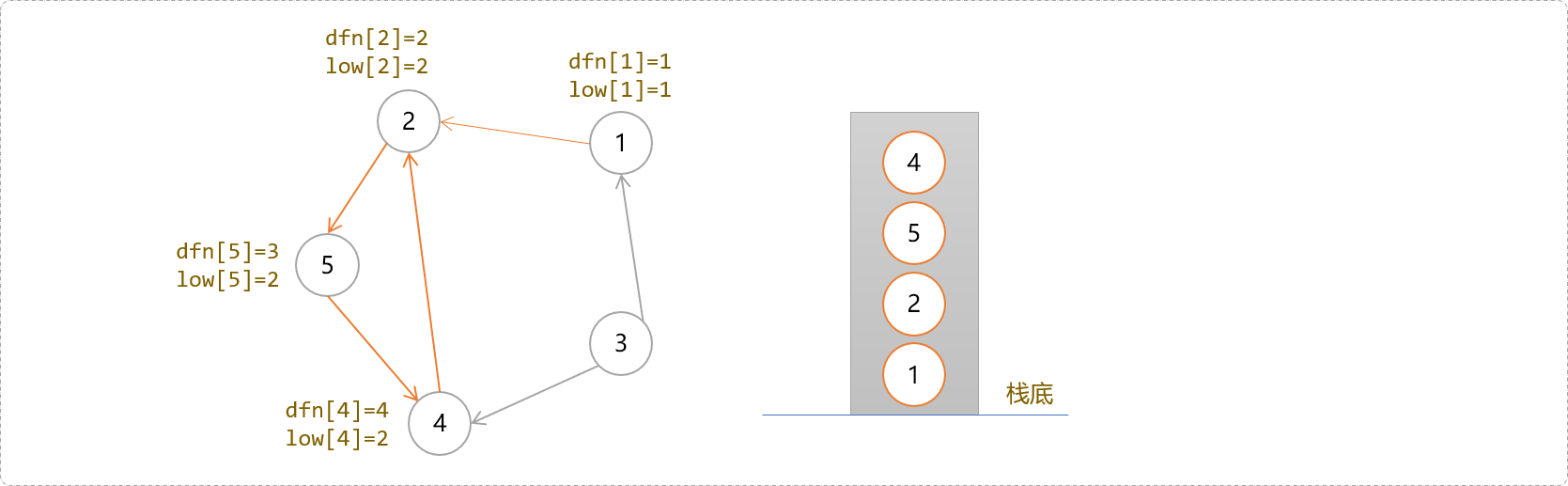
4号节点除了2号节点外没有其它子节点,搜索结束,回溯到4号,因其dfs[4]!=low[4],暂时不要出栈,继续回溯到5号节点,因为dfs[5]!=low[5],不出栈。继续回溯到2号节点,因其dfs[2]==low[2],说明一个强连通分量到2号节点结束。把它们从栈中弹出来,得到第一个强连通分量上的所有节点。
**Tips:**如果
i节点的dfn[i]!=low[i],说明其节点可以回到更早的祖先。也说明,其在以祖先开始的强连通分量上。所以只有一直回溯到祖先时,才能一一出栈。Tarjan算法求解强连通分量中,栈起到了至关重要的作用。一旦发现一个强连通分量,就会把这个强连通分量上的节点弹出来。所以访问过、但是不在栈中的节点说明已经加入到了另一个强连通分量上。如果访问过,但是还在栈中的节点说明还没有找到归属。
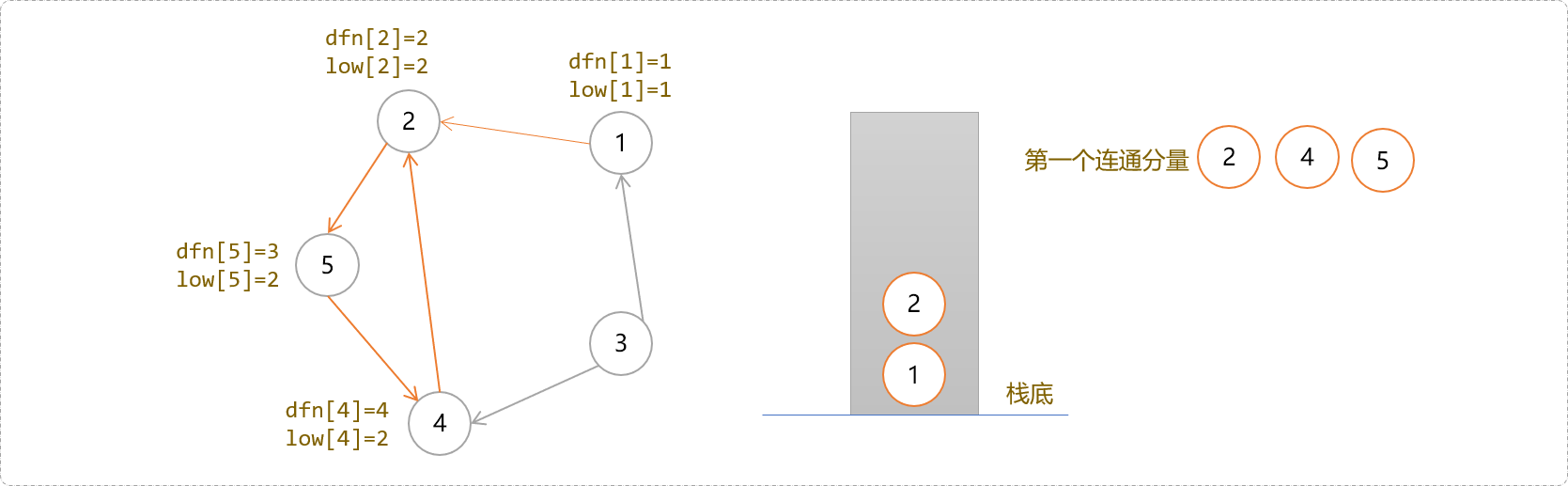
- 回溯到
1号节点时,因dfn[1]=low[1]。1号节点构成只有一个节点的强连通分量。
小结:
- **深度搜索阶段:**如果
u节点的子节点v已经访问、且在栈中。说明v是u的祖先,更新u的low值。同时更新u的除了v之外祖先的low值。 - **回溯阶段:**如果
u节点的dfn!=low,继续向上回溯, 如果u节点的dfn==low,说明找到了一个强连通分量,把栈中u节点(包含u)之上的节点全部弹出来。
编码实现
#include<iostream>
#include<stack>
#include<vector>
using namespace std;
//节点数、边数
int n,m;
//dfn记数器和强连通分量记数器
int cnt,cntb;
//矩阵存储图
vector<int> edge[101];
//记录强连通分量
vector<int> connections[101];
//是否在栈中
bool inSta[101];
//时间戳
int dfn[101];
//回溯值
int low[101];
//栈
stack<int> s;void getConn(int u) {++cnt;//前序位置记录节点的时间戳和回溯值dfn[u]=low[u]=cnt;//入栈s.push(u);inSta[u]=true;//遍历子节点for(int i=0; i<edge[u].size(); ++i) {int v=edge[u][i];if(!dfn[v]) {//没有被访问getConn(v);//回溯位置,根据子节点的 low 更新父节点的 lovwlow[u]=min(low[u],low[v]);} else if(inSta[v])//访问过且在栈中,遇到了回边。更新 low 为祖先节点的时间戳low[u]=min(low[u],dfn[v]);}//后序遍历位置if(dfn[u]==low[u]) {//如果时间戳和回溯值相同,找到一条强连通分量++cntb;int t;do {t=s.top();s.pop();inSta[t]=false;connections[cntb].push_back(t);} while(t!=u);}
}
int main() {cin>>n>>m;for(int i=1; i<=m; ++i) {int u,v;cin>>u>>v;edge[u].push_back(v);}getConn(1);for(int i=1; i<=cntb; ++i) {cout<<"conn: "<<i<<" : ";for(int j=0; j<connections[i].size(); ++j)cout<<connections[i][j]<<" ";cout<<endl;}return 0;
}
//测试数据
//7 11
//1 2
//2 3
//2 5
//2 4
//3 5
//3 7
//7 5
//5 6
//6 7
//4 1
//4 5
思考一下,如下图的强连通分量有几个。
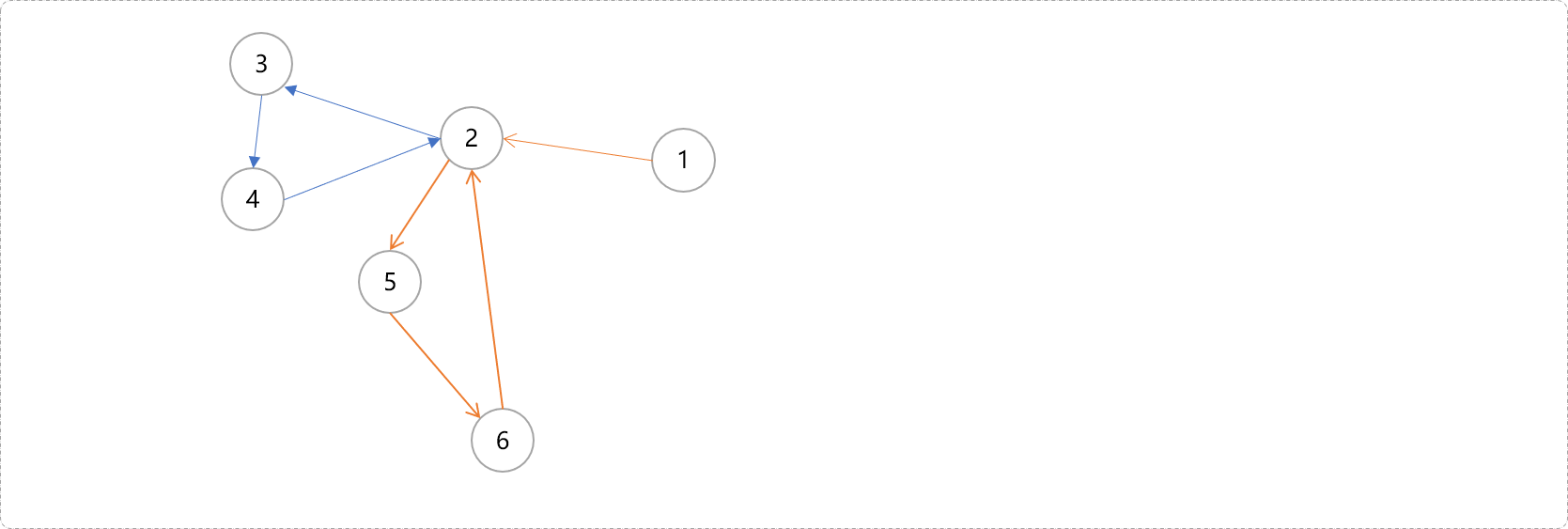
答案:有两个,分别是
6 5 4 3 21
3. 总结
强连通分量算法还有Kosaraju 、Garbow 算法。有兴趣者可自行了解。
相关文章:

C++图论之强连通图
1. 连通性 什么是连通性? 连通,字面而言,类似于自来水管道中的水流,如果水能从某一个地点畅通流到另一个地点,说明两点之间是连通的。也说明水管具有连通性,图中即如此。 无向图和有向图的连通概念稍有差…...

SadTalker数字人增加视频输出mp4质量精度
最近在用数字人简易方案,看到了sadtalker虽然效果差,但是可以作为一个快速方案,没有安装sd的版本,随便找了个一键安装包 设置如上 使用倒是非常简单,但是出现一个问题,就是输出的mp4都出马赛克了 界面上却…...
swing快速入门(三十二)消息对话框
注释很详细,直接上代码 上一篇 新增内容 1.自定义对话框前列图标 2.消息对话框的若干种形式 package swing21_30;import javax.swing.*; import java.awt.*; import java.awt.event.ActionEvent;public class swing_test_30 {// 定义一个JFrameJFrame jFrame n…...
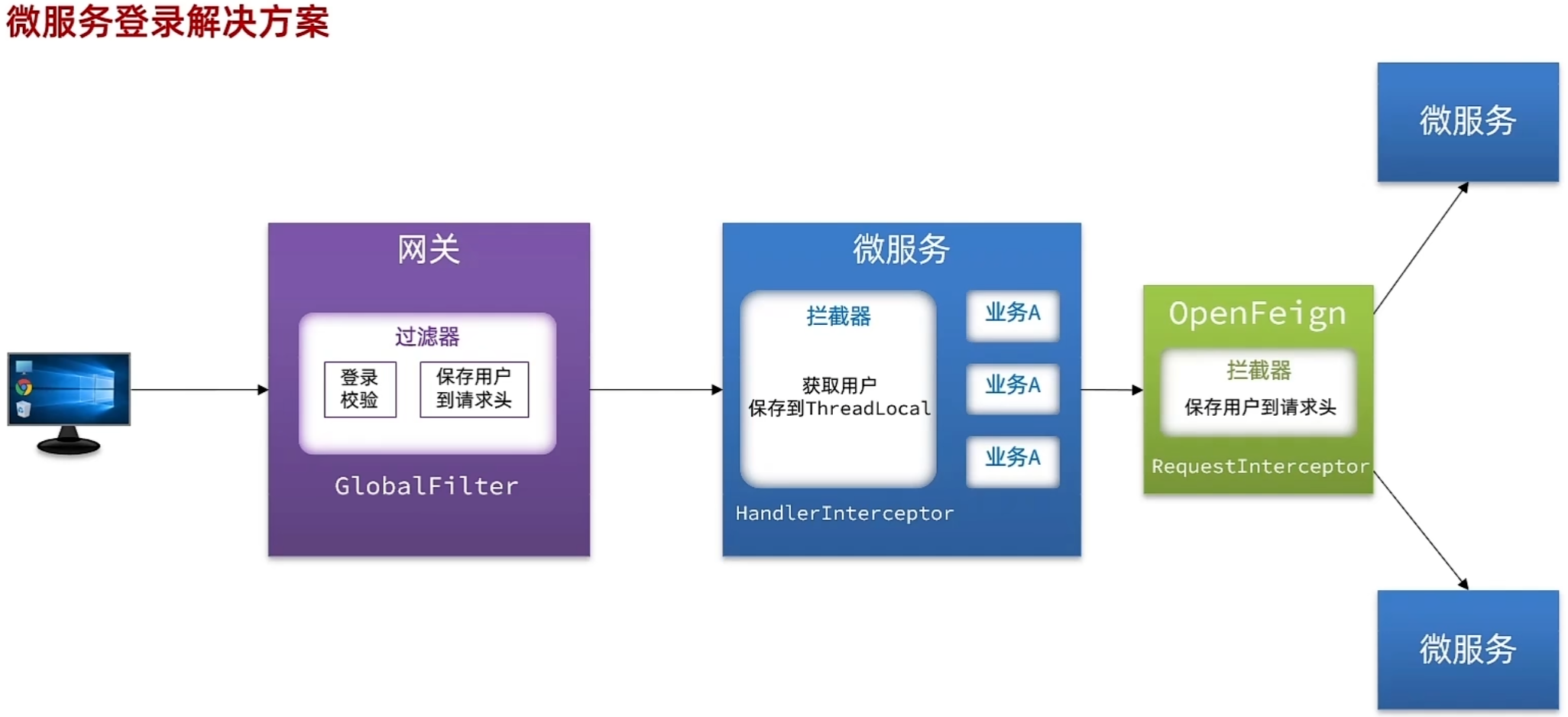
《Spring Cloud学习笔记:Nacos配置管理 OpenFeign LoadBalancer Getway》
基于Feign的声明式远程调用(代码更优雅),用它来去代替我们之前的RestTemplate方式的远程调用 1. Nacos配置管理:Nacos Config 服务配置中心介绍 首先我们来看一下,微服务架构下关于配置文件的一些问题: 配置文件相…...

深入解析 Flink CDC 增量快照读取机制
一、Flink-CDC 1.x 痛点 Flink CDC 1.x 使用 Debezium 引擎集成来实现数据采集,支持全量加增量模式,确保数据的一致性。然而,这种集成存在一些痛点需要注意: 一致性通过加锁保证:在保证数据一致性时,Debez…...

060:vue中markdown编辑器mavon-editor的应用示例
第060个 查看专栏目录: VUE ------ element UI 专栏目标 在vue和element UI联合技术栈的操控下,本专栏提供行之有效的源代码示例和信息点介绍,做到灵活运用。 (1)提供vue2的一些基本操作:安装、引用,模板使…...

使用SCP在Linux中安全复制文件:参数详解
SCP(Secure Copy)是一个在Linux和其他类Unix系统中使用的命令行工具,用于在本地和远程主机之间安全地复制文件和目录。本文将详细介绍SCP的多个常用参数,并通过示例进行说明。 基本语法 scp [options] source destination其中&a…...

【动态规划精选题目】3、简单多状态模型
此动态规划系列主要讲解大约10个系列【后续持续更新】 本篇讲解简单多状态模型中的9道经典题,会在讲解题目同时给出AC代码 目录 1、按摩师 2、力扣198:打家劫舍1 3、打家劫舍II 4、删除并获得点数 5、 粉刷房子 6、力扣309:买卖股票的最佳时机含冷冻期 7、 买…...

软件测试/测试开发丨Python 虚拟环境及pip环境管理
venv 虚拟环境管理 venv 虚拟环境的优点 独立的 Python 环境,不会产生冲突有助于包的管理删除和卸载方便 venv 使用方法 创建虚拟环境 python3 -m venv test 激活虚拟环境 切换指定文件夹Windows:/Scripts/macOS:/bin/ 执行指令ÿ…...

Mybatis SQL构建器类 - SQL类
下面是一些例子: // Anonymous inner class public String deletePersonSql() {return new SQL() {{DELETE_FROM("PERSON");WHERE("ID #{id}");}}.toString(); }// Builder / Fluent style public String insertPersonSql() {String sql new…...

海云安亮相2023北京国际金融安全论坛,助力金融企业数字化转型降本增效
近日,2023北京国际金融安全论坛暨金融科技标准认证生态大会在北京金融安全产业园成功举办。深圳海云安网络安全技术有限公司(以下简称“海云安”)受邀参展亮相此次大会。海云安作为国内领先的金融科技服务商,展示了开发安全系列产…...
nodeJS搭建免费代理IP池爬取贴吧图片实战
之前用python写过爬虫,这次想试试nodeJS爬虫爬取贴吧图片,话不多说代码如下,爬取制定吧的前十页所有帖子里的图片 爬取贴吧图片脚本 你得提前创建一个images文件夹 const axios require("axios"); const cheerio require("…...
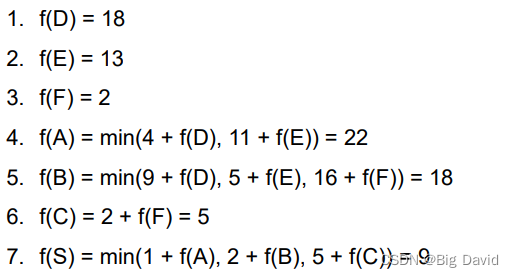
基于图搜索的自动驾驶规划算法 - BFS,Dijstra,A*
本文将讲解BFS,Dijstra,A*,动态规划的算法原理,不正之处望读者指正,希望有兴趣的读者能在评论区提出一些这些算法的面试考点,共同学习,一起进步 0 图论基础 图有三种:无向图、有向…...
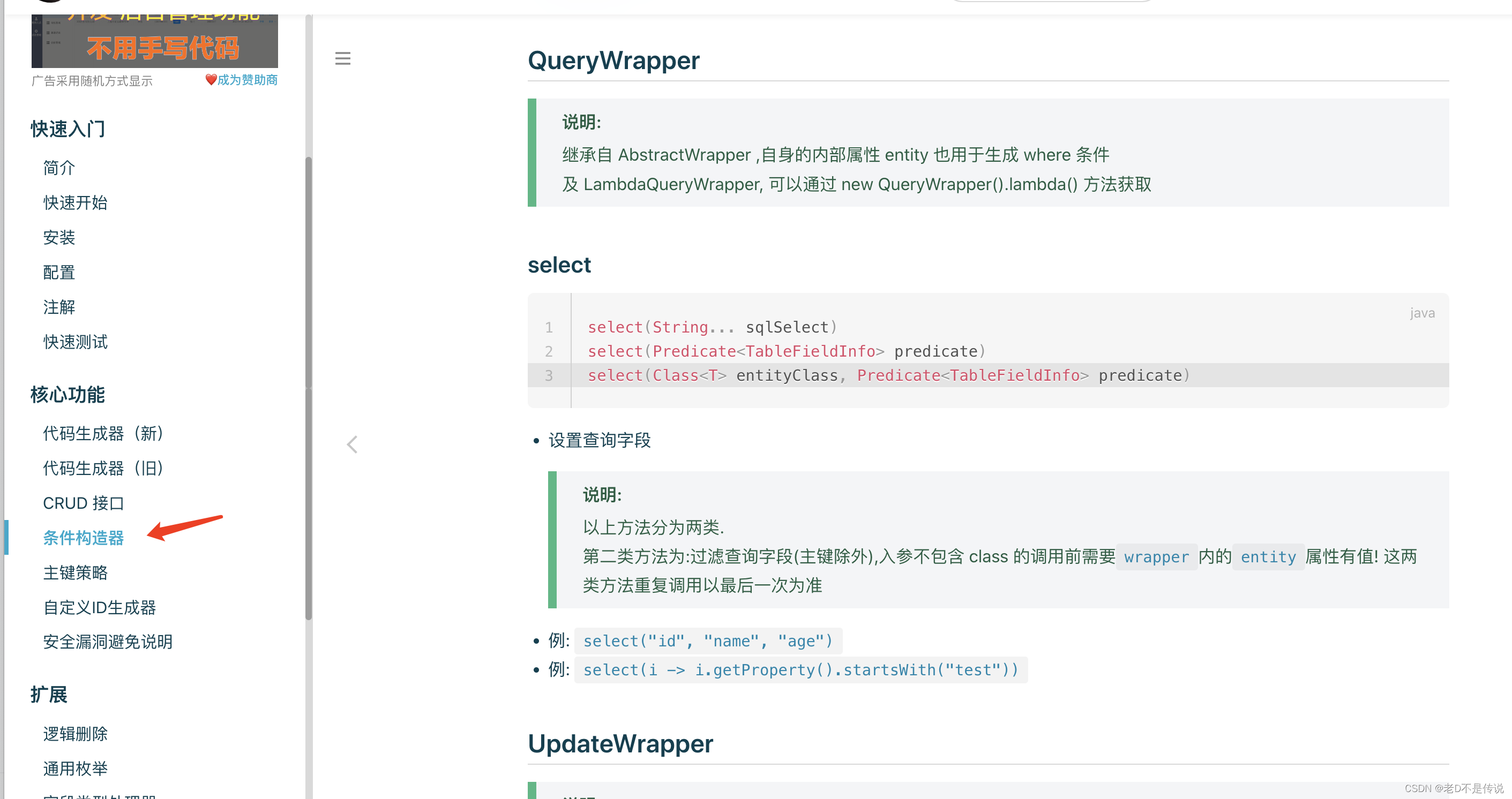
Spring系列学习四、Spring数据访问
Spring数据访问 一、Spring中的JDBC模板介绍1、新建SpringBoot应用2、引入依赖:3、配置数据库连接,注入dbcTemplate对象,执行查询:4,测试验证: 二、整合MyBatis Plus1,在你的项目中添加MyBatis …...
)
HBase 创建不分裂的表 ( 禁止 Table Split )
注意:由于 HBase 版本众多,配置表的语法在不同版本上会有差异,本文介绍的配置方法是在 1.4.9 版本上测试的,使用 HBase 2.0 的版本需要核实并修改相关配置方法! 有时候,出于特殊需要,我们希望对…...

docker入门概念详解
本篇文章对docker的一些基础概念和周边概念进行了详细解释。帮助你可以很好的理解docker是用来干什么的,docker是怎么工作的。其中有docker所运用到的技术解释,docker的不同发展版本,dokcer的架构,docker的生态等等详解。希望本片…...

C++程序设计实践报告【格式】
C程序设计实践报告 原XX工业学院 C程序设计实践报告 题目: 专业: 学号: 姓名: 年 月 日 目录 一、绪…...

浅谈数据仓库运营
一、背景 企业每天都会产生大量的数据,随着时间增长,数据会呈现几何增长,尤其在系统基建基础好的公司。好的数据仓库需要提前规划和好的运营,才能支持企业的发展,为企业提供数据分析基础。 二、目标 提高数据仓库存储…...
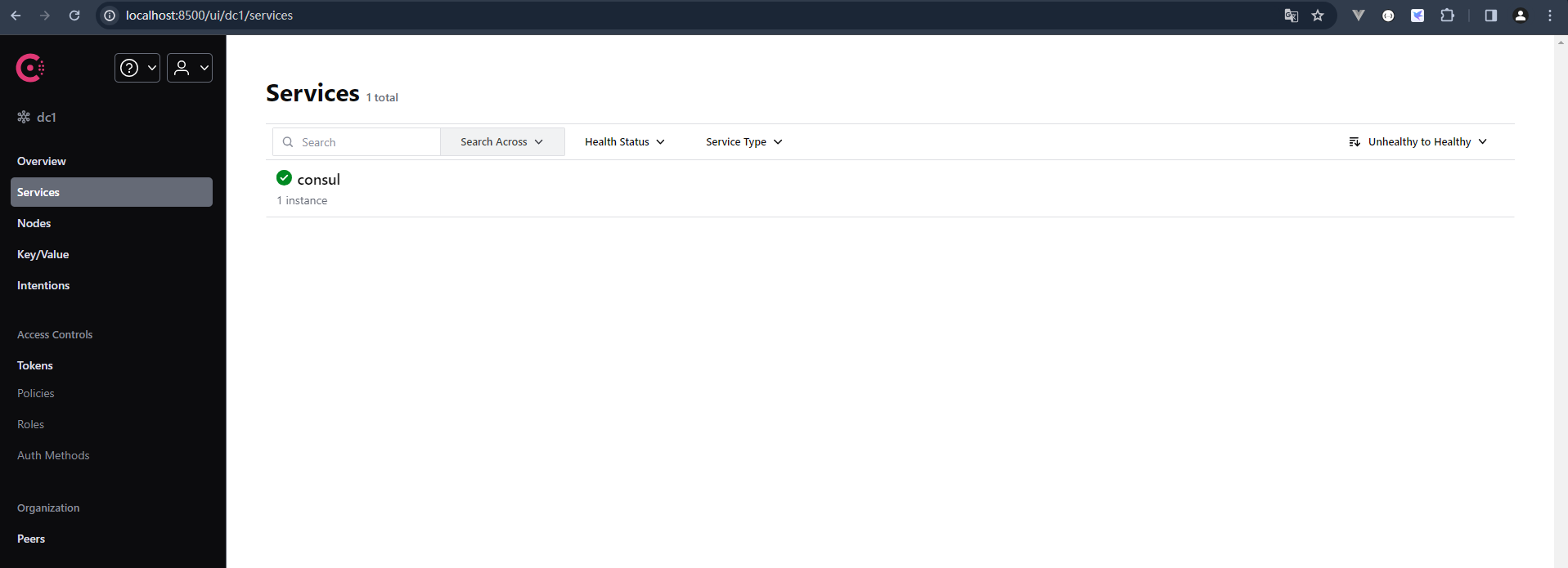
系列六、Consul
一、Consul 1.1、概述 Consul是一套开源的分布式服务发现和配置管理系统,由HashiCorp公司用Go语言开发。他提供了微服务系统中的服务治理、配置中心、控制总线等功能。这些功能中的每一个功能都可以单独使用,也可以一起使用以构建全方位的服务网格&…...

Java集合/泛型篇----第一篇
系列文章目录 文章目录 系列文章目录前言一、ArrayList和linkedList的区别二、HashMap和HashTable的区别三、Collection包结构,与Collections的区别四、泛型常用特点前言 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

《Offer来了:Java面试核心知识点精讲》大纲
文章目录 一、《Offer来了:Java面试核心知识点精讲》的典型大纲框架Java基础并发编程JVM原理数据库与缓存分布式架构系统设计二、《Offer来了:Java面试核心知识点精讲(原理篇)》技术文章大纲核心主题:Java基础原理与面试高频考点Java虚拟机(JVM)原理Java并发编程原理Jav…...

【阅读笔记】MemOS: 大语言模型内存增强生成操作系统
核心速览 研究背景 研究问题:这篇文章要解决的问题是当前大型语言模型(LLMs)在处理内存方面的局限性。LLMs虽然在语言感知和生成方面表现出色,但缺乏统一的、结构化的内存架构。现有的方法如检索增强生成(RA…...
