最优化方法Python计算:无约束优化应用——逻辑分类模型
逻辑回归模型更多地用于如下例所示判断或分类场景。
例1 某银行的贷款用户数据如下表:
| 欠款(元) | 收入(元) | 是否逾期 | |
|---|---|---|---|
| 1 | 7000 | 800 | Yes |
| 2 | 2000 | 2500 | No |
| 3 | 5000 | 3000 | Yes |
| 4 | 4000 | 4000 | No |
| 5 | 2000 | 3800 | No |
显然,客户是否逾期(记为 y y y)与其欠款额(记为 x 1 x_1 x1)和收入(记为 x 2 x_2 x2)相关。如果将客户逾期还款记为1,未逾期记为0,我们希望根据表中数据建立 R 2 → { 0 , 1 } \text{R}^2\rightarrow\{0,1\} R2→{0,1}的拟合函数
y = F ( x ) y=F(\boldsymbol{x}) y=F(x)
使得 F ( x i ) ≈ y i , i = 1 , 2 , ⋯ , 5 F(\boldsymbol{x}_i)\approx y_i,i=1,2,\cdots,5 F(xi)≈yi,i=1,2,⋯,5,并用 F ( x ) F(\boldsymbol{x}) F(x)根据新客户的欠款额与收入数据
| 欠款(元) | 收入(元) | 是否逾期 |
|---|---|---|
| 3500 | 3500 | ? |
| 3000 | 2100 | ? |
进行预测分类。
要用回归模型分类,关键在于如何将预测值 y y y离散化为0,1,或一般地离散化为连续的 n n n个整数 N 1 , N 1 + 1 , ⋯ , N 1 + n − 1 , N 2 N_1, N_1+1,\cdots,N_1+n-1,N_2 N1,N1+1,⋯,N1+n−1,N2。解决之道是设置阈值,譬如,设 μ 1 = N 1 + 0.5 , μ 2 = N 1 + 1.5 , ⋯ , μ n − 1 = N 1 + n − 0.5 \mu_1=N_1+0.5,\mu_2=N_1+1.5,\cdots,\mu_{n-1}=N_1+n-0.5 μ1=N1+0.5,μ2=N1+1.5,⋯,μn−1=N1+n−0.5,对 y < μ 1 y<\mu_1 y<μ1, y y y转换为 N 1 N_1 N1; μ i ≤ y < μ i + 1 \mu_i\leq y<\mu_{i+1} μi≤y<μi+1,将其转化为 N 1 + i N_1+i N1+i; y ≥ μ n − 1 y\geq\mu_{n-1} y≥μn−1,转换为 N 2 N_2 N2。
其次,对分类模型的评价指标应该是分类正确率:设 ( x i , y i ) (\boldsymbol{x}_i,y_i) (xi,yi), i = 1 , 2 , ⋯ , m i=1,2,\cdots,m i=1,2,⋯,m为测试数据。用训练所得的最优模式 w 0 \boldsymbol{w}_0 w0,得预测值 y i ′ y'_i yi′, i = 1 , 2 , ⋯ , m i=1,2,\cdots,m i=1,2,⋯,m。记 y = ( y 1 y 2 ⋮ y m ) \boldsymbol{y}=\begin{pmatrix}y_1\\y_2\\\vdots\\y_m\end{pmatrix} y= y1y2⋮ym , y t = ( y 1 ′ y 2 ′ ⋮ y m ′ ) \boldsymbol{y}_t=\begin{pmatrix}y'_1\\y'_2\\\vdots\\y'_m\end{pmatrix} yt= y1′y2′⋮ym′ ,计算 y i = y i ′ y_i=y'_i yi=yi′成立的个数 m 1 m_1 m1,则正确率为 m 1 m × 100 \frac{m_1}{m}\times100 mm1×100。
下列代码实现用于分类的Classification类。
import numpy as np #导入numpy
class Classification(): #分类模型def threshold(self, x): #阈值函数N1 = x.min().astype(int) - 1 #最小阈值整数部分N2 = np.round(x.max()).astype(int) + 1 #最大阈值整数部分y = np.array([N1] * x.size) #因变量数组for n in range(N1, N2): #对每个可能的函数值d = np.where((x >= n - 0.5)&(x < n + 0.5)) #取值区间y[d] = n #函数值if(y.size == 1): #单值情形y = y[0]return ydef predict(self, X): #重载预测函数yp = RegressModel.predict(self, X) #计算预测值return self.threshold(yp) #转换为离散值def accuracy(self, y1, y2): #正确率m = y1.sizeacc=np.where(y1 == y2)[0].size #计算两者相等的元素个数return acc / m * 100def test(self, x, y): #测试函数yp = self.predict(x)return yp, self.accuracy(y, yp)
class LogicClassifier(Classification, LogicModel):'''逻辑分类模型'''
程序中第2~22行定义了用于分类的Classification辅助类。其中第3~12行定义阈值函数threshold。第13~15行在预测函数predict外“套上”阈值函数threshold,筛选出分类值返回。第16~19行定义计算两个等长整数数组y1,y2中对应元素相等的比率函数accuracy。第20~22行定义测试函数test,对测试数据x和y,计算x的预测值yp,然后调用accuracy计算y和yt的相等比率返回。第23~24行联合Classification类和LogicModel类(详见博文《最优化方法Python计算:无约束优化应用——逻辑回归模型》)实现逻辑分类模型类LogicClassifier。下面我们来小试牛刀:用逻辑分类模型LogicClassifier计算例1中的问题。
import numpy as np #导入numpy
x = np.array([[7000, 800], #设置训练、测试数据[2000, 2500],[5000, 3000],[4000, 4000],[2000, 3800]])
y = np.array([1, 0, 1, 0, 0])
title = np.array(['No', 'Yes']) #预测值标签
np.random.seed(2024) #随机种子
credit = LogicClassifier() #创建逻辑分类模型
credit.fit(x,y) #训练
_, acc=credit.test(x,y) #测试
print('准确率:%.1f'%acc + '%')
x1 = np.array([[3500, 3500], #设置预测数据[3000, 2100]])
print('对测试数据:')
print(x1)
Y = credit.predict(x1) #计算预测值
print('归类为:')
print([title[y] for y in Y])
看官可借助代码内注释信息理解程序,需要提请注意的是第9行设置随机种子是为了使看官的运行结果与下列的输出一致。运行程序,输出
训练中...,稍候
3次迭代后完成训练。
准确率:100.0%
对测试数据:
[[3500 3500][3000 2100]]
归类为:
['No', 'Yes']
开胃菜后,上正餐。
综合案例
文件iris.csv(来自UC Irvine Machine Learning Repository)是统计学家R. A. Fisher在1936年采集的一个小型经典数据集,这是用于评估分类方法的最早的已知数据集之一。该数据集含有150例3种鸢尾花:setosa、versicolour和virginica的数据
| Sepal.Length | Sepal.Width | Petal.Length | Petal.Width | Species | |
|---|---|---|---|---|---|
| 1 | 5.1 | 3.5 | 1.4 | 0.2 | setosa |
| 2 | 4.9 | 3 | 1.4 | 0.2 | setosa |
| 3 | 4.7 | 3.2 | 1.3 | 0.2 | setosa |
| ⋯ \cdots ⋯ | ⋯ \cdots ⋯ | ⋯ \cdots ⋯ | ⋯ \cdots ⋯ | ⋯ \cdots ⋯ | ⋯ \cdots ⋯ |
| 51 | 7 | 3.2 | 4.7 | 1.4 | versicolor |
| 52 | 6.4 | 3.2 | 4.5 | 1.5 | versicolor |
| 53 | 6.9 | 3.1 | 4.9 | 1.5 | versicolor |
| ⋯ \cdots ⋯ | ⋯ \cdots ⋯ | ⋯ \cdots ⋯ | ⋯ \cdots ⋯ | ⋯ \cdots ⋯ | ⋯ \cdots ⋯ |
| 148 | 6.5 | 3 | 5.2 | 2 | virginica |
| 149 | 6.2 | 3.4 | 5.4 | 2.3 | virginica |
| 150 | 5.9 | 3 | 5.1 | 1.8 | virginica |
五个数据属性的意义分别为
- Sepal.Length:花萼长度;
- Sepal.Width:花萼宽度;
- Petal.Length:花瓣长度;
- Petal.Width:花瓣宽度;
- Species:种类。
下列代码从文件中读取数据,将花的种类数字化。
import numpy as np #导入numpy
data = np.loadtxt('iris.csv', delimiter=',', dtype=str) #读取数据文件
X = np.array(data) #转换为数组
X = X[:, 1:] #去掉编号
title = X[0, :4] #读取特征名称
X = X[1:, :] #去掉表头
Y = X[:, 4] #读取标签数据
X = X[:, :4].astype(float)
m = X.shape[0] #读取样本个数
print('共有%d个数据样本'%m)
print('鸢尾花特征数据:')
print(X)
Y = np.array([0 if y == 'setosa' else #类别数值化1 if y == 'versicolor' else2 for y in Y])
print('鸢尾花种类数据:')
print(Y)
运行程序,输出
共有150个数据样本
鸢尾花特征数据:
[[5.1 3.5 1.4 0.2][4.9 3. 1.4 0.2][4.7 3.2 1.3 0.2]
...[6.5 3. 5.2 2. ][6.2 3.4 5.4 2.3][5.9 3. 5.1 1.8]]
鸢尾花种类数据:
[0 0 0 ... 2 2 2]
花萼的长度、宽度,花瓣的长度、宽度对鸢尾花的种类有明显的相关性。接下来我们要从数据集中随机选取一部分作为训练数据,训练LogicClassifier分类模型,然后用剩下的数据进行测试,评价训练效果。在前面的程序后添加以下代码
……
a = np.arange(m) #数据项下标
np.random.seed(2024)
index = np.random.choice(a,m//3,replace=False) #50个随机下标
Xtrain = X[index] #训练数据
Ytrain = Y[index]
index1 = np.setdiff1d(a,index) #测试数据下标
Xtest = X[index1] #测试数据
Ytest = Y[index1]
iris = LogicClassifier() #创建模型
print('随机抽取%d个样本作为训练数据。'%(m//3))
iris.fit(Xtrain,Ytrain) #训练模型
_, accuracy = iris.test(Xtest,Ytest) #测试
print('对其余%d个数据测试,分类正确率为%.2f'%(m-m//3,accuracy)+'%')
运行程序输出
……
随机抽取50个样本作为训练数据。
训练中...,稍候
23次迭代后完成训练。
对其余100个数据测试,分类正确率为99.00%
第1行的省略号表示前一程序的输出。从测试结果可见训练效果效果不错!
相关文章:

最优化方法Python计算:无约束优化应用——逻辑分类模型
逻辑回归模型更多地用于如下例所示判断或分类场景。 例1 某银行的贷款用户数据如下表: 欠款(元)收入(元)是否逾期17000800Yes220002500No350003000Yes440004000No520003800No 显然,客户是否逾期ÿ…...
springboot定时执行某个任务
springboot定时执行某个任务 要定时执行的方法加上Schedule注解 括号内跟 cron表达式 “ 30 15 10 * * ?” 代表秒 分 时 日 月 周几 启动类上加上EnableScheduling 注释...

Java EE Servlet之Servlet API详解
文章目录 1. HttpServlet1.1 核心方法 2. HttpServletRequest3. HttpServletResponse 接下来我们来学习 Servlet API 里面的详细情况 1. HttpServlet 写一个 Servlet 代码,都是要继承这个类,重写里面的方法 Servlet 这里的代码,只需要继承…...

neo4j运维管理
管理数据库 概念 Neo4j 5(从v4.0),可以同时创建和使用多个活动数据库。 DBMS Neo4j是一个数据库管理系统(DBMS),能够管理多个数据库。DBMS可以管理一个独立的服务器,也可以管理集群中的一组服务器。 实例 Neo4j实例是运行Neo4j服务器代…...
【MYSQL】-函数
💖作者:小树苗渴望变成参天大树🎈 🎉作者宣言:认真写好每一篇博客💤 🎊作者gitee:gitee✨ 💞作者专栏:C语言,数据结构初阶,Linux,C 动态规划算法🎄 如 果 你 …...
传统船检已经过时?AR智慧船检来助力!!
想象一下,在茫茫大海中,一艘巨型货轮正缓缓驶过。船上的工程师戴着一副先进的AR眼镜,他们不再需要反复翻阅厚重的手册,一切所需信息都实时显示在眼前。这不是科幻电影的场景,而是智慧船检技术带来的现实变革。那么问题…...

JAVA进化史: JDK11特性及说明
JDK 11(Java Development Kit 11)是Java平台的一个版本,于2018年9月发布。这个版本引入了一些新特性和改进,以下是其中一些主要特性。 HTTP Client(标准化) JDK 11引入了一个新的HTTP客户端,用…...
模型 安索夫矩阵
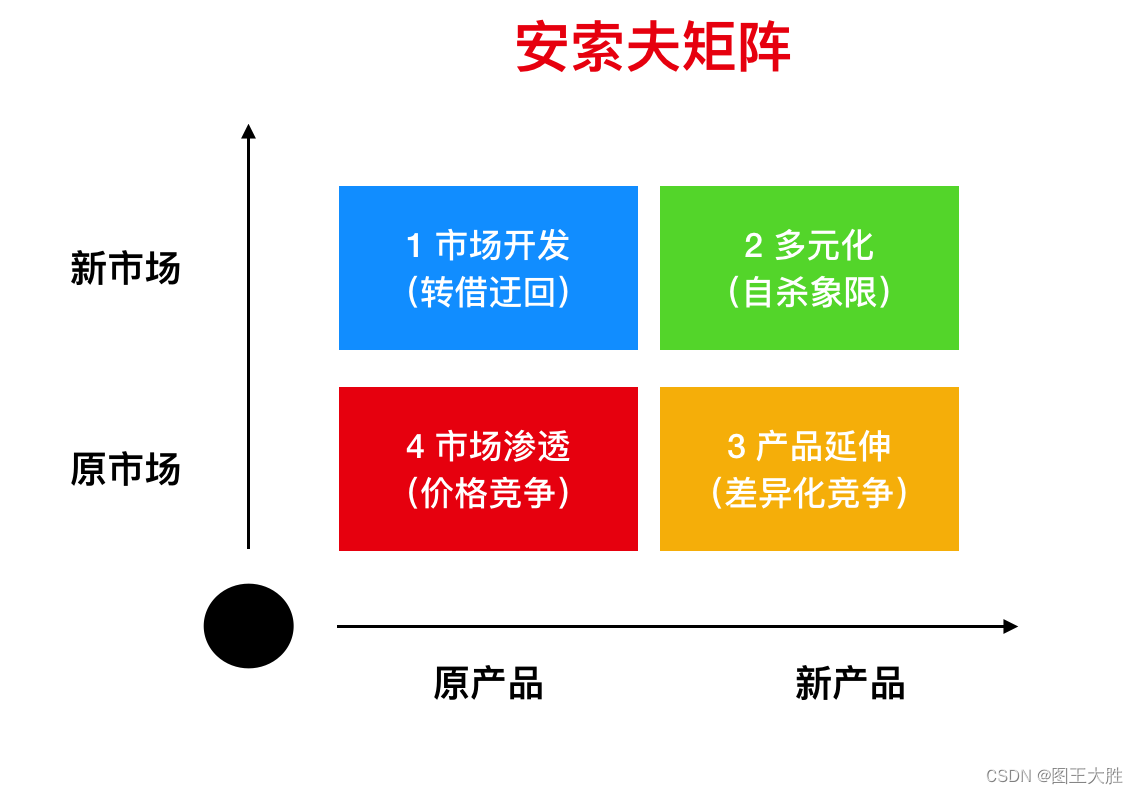
本系列文章 主要是 分享模型,涉及各个领域,重在提升认知。产品市场战略。 1 安索夫矩阵的应用 1.1 江小白的多样化经营策略 使用安索夫矩阵来分析江小白市场战略。具体如下: 根据安索夫矩阵,江小白的现有产品是其白酒产品&…...

性能手机新标杆,一加 Ace 3 发布会定档 1 月 4 日
12 月 27 日,一加宣布将于 1 月 4 日发布新品一加 Ace 3。一加 Ace 系列秉持「产品力优先」理念,从一加 Ace 2、一加 Ace 2V 到一加 Ace 2 Pro,款款都是现象级爆品,得到了广大用户的认可与支持。作为一加 2024 开年之作࿰…...

Vue 框架前导:详解 Ajax
Ajax Ajax 是异步的 JavaScript 和 XML。简单来说就是使用 XMLHttpRequest 对象和服务器通信。可以使用 JSON、XML、HTML 和 text 文本格式来发送和接收数据。具有异步的特性,可在不刷新页面的情况下实现和服务器的通信,交换数据或者更新页面 01. 体验 A…...

3分钟快速安装 ClickHouse、配置服务、设置密码和远程登录以及修改数据目录
下面是一个完整的 ClickHouse 安装和配置流程,包括安装 ClickHouse、配置服务、设置密码和远程登录以及修改数据目录。 安装 ClickHouse 安装 YUM 工具包: sudo yum install -y yum-utils添加 ClickHouse YUM 仓库: sudo yum-config-manager…...

PHP8使用PDO对象增删改查MySql数据库
PDO简介 PDO(PHP Data Objects)是一个PHP扩展,它提供了一个数据库访问层,允许开发人员使用统一的接口访问各种数据库。PDO 提供了一种用于执行查询和获取结果的简单而一致的API。 以下是PDO的一些主要特点: 统一接口…...
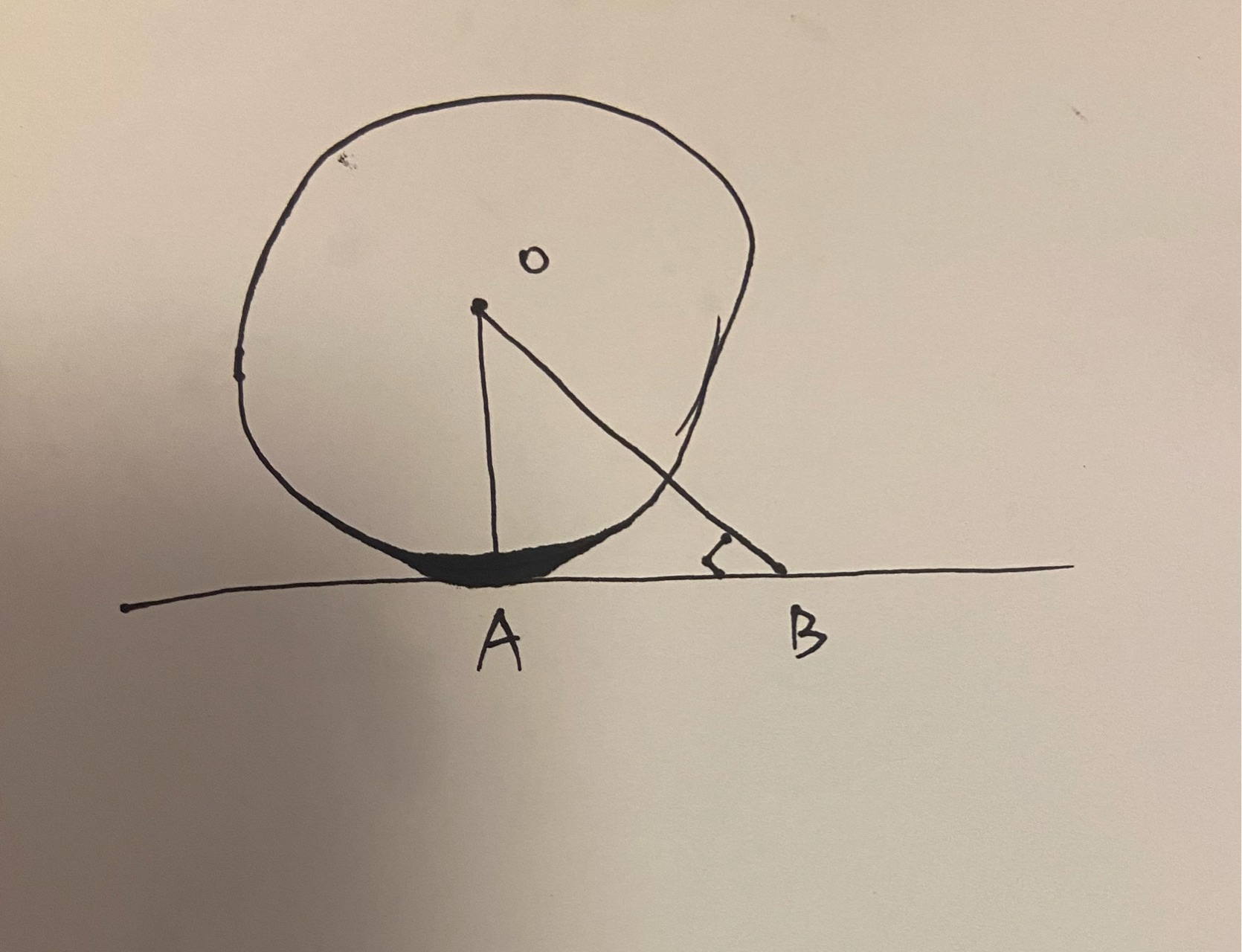
证明:切线垂直于半径
证明: 切线垂直于过切点的半径。 下面是网上最简单的证明方法。 证明: 利用反证法。 如下图所示,直线AB和圆O切于点A,假设OA 不垂直于 AB,而 O B ⊥ A B OB \perp AB OB⊥AB,则 ∠ O B A 90 \angle OB…...
普中STM32-PZ6806L开发板(STM32CubeMX创建项目并点亮LED灯)
简介 搭建一个用于驱动 STM32F103ZET6 GPIO点亮LED灯的任务;电路原理图 LED电路原理图 芯片引脚连接LED驱动引脚原理图 创建一个点亮LED灯的Keil 5项目 创建STM32CubeMX项目 New Project -> 单击 -> 芯片搜索STM32F103ZET6->双击创建 初始化时钟 调试设置 一…...
【Windows】共享文件夹拍照还原防火墙设置(入站,出站设置)---图文并茂详细讲解
目录 一 共享文件夹(两种形式) 1.1 普通共享与高级共享区别 1.2 使用 二 拍照还原 2.1 是什么 2.2 使用 三 防火墙设置(入栈,出站设置) 3.1 引入 3.2 入站出站设置 3.2.1入站出站含义 3.3入站设置 3.4安装jdk 3.5使用tomcat进行访…...
1.决策树
目录 1. 什么是决策树? 2. 决策树的原理 2.1 如何构建决策树? 2.2 构建决策树的数据算法 2.2.1 信息熵 2.2.2 ID3算法 2.2.2.1 信息的定义 2.2.2.2 信息增益 2.2.2.3 ID3算法举例 2.2.2.4 ID3算法优缺点 2.2.3 C4.5算法 2.2.3.1 C4.5算法举例 2.2.4 CART算法 2.2.4…...

基于微信小程序的停车预约系统设计与实现
基于微信小程序的停车预约系统设计与实现 项目概述 本项目旨在结合微信小程序、后台Spring Boot和MySQL数据库,打造一套高效便捷的停车预约系统。用户通过微信小程序进行注册、登录、预约停车位等操作,而管理员和超级管理员则可通过后台管理系统对停车…...

再见2023,你好2024
再见2023,你好2024 生活1月 悲伤与治愈2~4月 运动与偏爱5月 体验与美食6月 婚礼与热爱7~8月 就医与别离9~11月 陪伴与暖房12月 体验&新生 运动追剧读书总结 生活 生活是一个修罗场,来世间一场,要经历丰腴有趣的人生。去体验各种滋味&…...

年度总结|存储随笔2023年度最受欢迎文章榜单TOP15-part1
原创 古猫先生 存储随笔 2023-12-31 08:31 发表于上海 回首2023 2-8月份有近半年时间基本处于断更状态 好在8月份后小编没有松懈 (虽然2023年度总结,更像是近4个月总结) 本年度顺利加V啦! 感谢各位粉丝朋友的一路支持与陪伴 …...

微信小程序 手机号授权登录 偶尔后端解密失败
微信小程序wx.login获取code要在手机号授权前触发 <button:id"code":open-type"hasGetPrivacySetting ? getPhoneNumber|agreePrivacyAuthorization : getPhoneNumber"getphonenumber"onGetPhoneNumber"class"btn"click"cli…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...
