拒绝采样(算法)总结
先说说什么是拒绝采样算法:就类似于数学上的求阴影面积的方法,直接求求不出来,就用大面积 - 小面积 = 阴影面积的办法。
所谓拒绝 和 采样 :就像是撒豆子计个数,计算概率问题一样,大桶里面套小桶,一把豆子撒下去,每个豆子都是一个“样本”,如果落在小桶外面的大桶里面去了,就“拒绝”这个样本,如果在小桶里,就“采用”这个样本, 就这样拒绝-和采用所有的豆子,小桶里面的豆子数量除以所有的豆子的数量就得到啊小桶在大桶里的占比,也就是豆子落在小桶里的概率……………………巴拉巴拉一些关于概率的问题就可以这样求解了。
这是力扣的两题,一一举例加以解释。

读题:现在有一个只能生成1、2、3、4、5、6、7这7个数字的随机函数Rand7(),问你如何用这个函数实现一个可以随机生成1~10的随机函数Rand10()(PS:随机函数,生成其中每个值的概率必须相等才行)
想法:想想二进制(011010010111000010101010)这玩意,用两个Rand7()就可以生成7*7=49种选择,我们只要10种就够了,所以可以有
1和1、1和2、1和3 表示 1
1和4、1和5、1和6 表示 2
2和1、2和2、2和3 表示 3
2和4、2和5、2和6 表示 4
3和1、3和2、3和3 表示 5
3和4、3和5、3和6 表示 6
4和1、4和2、4和3 表示 7
4和4、4和5、4和6 表示 8
5和1、5和2、5和3 表示 9
5和4、5和5、5和6 表示 10
6和1、6和2、6和3 (拒绝表示)
6和4、6和5、6和6 (拒绝表示)
7和1、7和2、7和3 (拒绝表示)
7和4、7和5、7和6 (拒绝表示)
也就是:第一个Rand7() 只能生成1~5中的一个数,第二个Rand7()只能生成1~6中的一个数,不然就拒绝采样,重新生成才行。
代码:(优化前)
class Solution {
public:int rand10() {int a,b;while(1){a = rand7();if( a != 6 && a != 7 ) break;}while(1){b = rand7();if( b != 7 ) break;}if( a == 1 ){if( b <= 3 ) return 1;else return 2;}else if( a == 2 ){if( b <= 3 ) return 3;else return 4;}else if( a == 3 ){if( b <= 3 ) return 5;else return 6;}else if( a == 4 ){if( b <= 3 ) return 7;else return 8;}else {if( b <= 3 ) return 9;else return 10;}}
};代码:(优化后)
class Solution {
public:int rand10() {while (true) {int num = (rand7() - 1) * 7 + rand7();if (num <= 40) return num % 10 + 1;}}
};不懂??????????没关系,看第二个,更简单!!!!!!!!!!!!!!!!!
第二题(别看题目,看下面读题)

读题:给一个半径 r0 和圆心坐标 x0, y0 ; 然后返回这个圆上或者圆内随机一点的坐标值(注:全是double类型,而且落在每一点上的概率必须相等)
官解:两个随机函数呗,一个随机范围是 [ x0-r0, x0+r0 ] ,另一个是[ y0-r0, y0+r0 ], 只要两个随机数的平方和大于了半径 r0 就统统 “拒绝”,只计算 平方和小于半径的结果,看图:
(这官解太low了)

这不就是撒豆子算概率问题嘛,随机生成的坐标点 x , y 就豆子的落点,这个落点只能在圆内,如果在圆外了就“拒绝”这个坐标,给我重新生成去。
(单纯是为了说明拒绝采样算法而已,此题有更佳的解法)
// 作者:力扣官方题解
class Solution {
private:mt19937 gen{random_device{}()};uniform_real_distribution<double> dis;double xc, yc, r;public:Solution(double radius, double x_center, double y_center): dis(-radius, radius), xc(x_center), yc(y_center), r(radius) {}vector<double> randPoint() {while (true) {double x = dis(gen), y = dis(gen);if (x * x + y * y <= r * r) {return {xc + x, yc + y};}}}
};最有解法:(极坐标法)
(这字丑自己都不想看)
代码:(并没有用拒绝采样算法,但是效率上是它的两倍,拒绝采样要170ms+,但是极坐标只需要80ms)
class Solution {
private:double rc,xc,yc;
public:Solution(double radius, double x_center, double y_center) {rc = radius;xc = x_center;yc = y_center;}vector<double> randPoint() {double Rx = rc * sqrt( (double)rand()/RAND_MAX );double angle = 2 * M_PI * (double)rand()/RAND_MAX;return { xc + Rx*cos(angle), yc + Rx*sin(angle)};}
};相关文章:

拒绝采样(算法)总结
先说说什么是拒绝采样算法:就类似于数学上的求阴影面积的方法,直接求求不出来,就用大面积 - 小面积 阴影面积的办法。 所谓拒绝 和 采样 :就像是撒豆子计个数,计算概率问题一样,大桶里面套小桶,…...
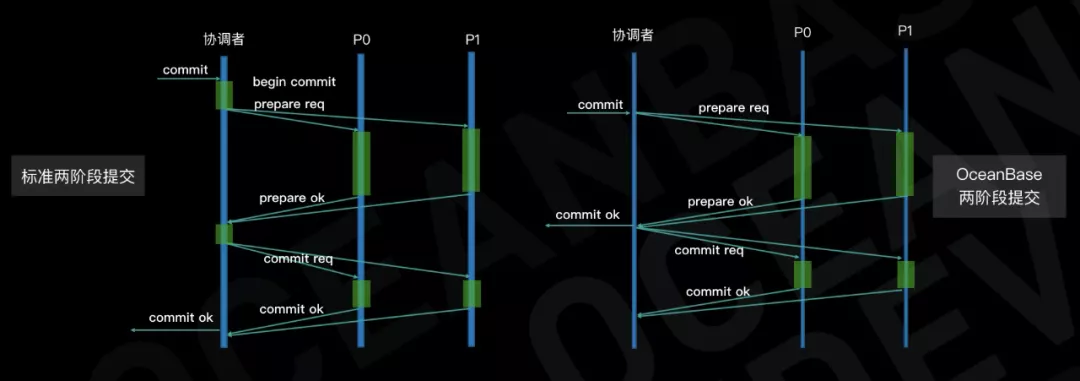
分布式数据库事务故障恢复的原理与实践
关系数据库中的事务故障恢复并不是一个新问题,自70年代关系数据库诞生之后就一直伴随着数据库技术的发展,并且在分布式数据库的场景下又遇到了一些新的问题。本文将会就事务故障恢复这个问题,分别讲述单机数据库、分布式数据库中遇到的问题和…...
Spark中的数据加载与保存
Apache Spark是一个强大的分布式计算框架,用于处理大规模数据。在Spark中,数据加载与保存是数据处理流程的关键步骤之一。本文将深入探讨Spark中数据加载与保存的基本概念和常见操作,包括加载不同数据源、保存数据到不同格式以及性能优化等方…...

2023-12-20 LeetCode每日一题(判别首字母缩略词)
2023-12-20每日一题 一、题目编号 2828. 判别首字母缩略词二、题目链接 点击跳转到题目位置 三、题目描述 给你一个字符串数组 words 和一个字符串 s ,请你判断 s 是不是 words 的 首字母缩略词 。 如果可以按顺序串联 words 中每个字符串的第一个字符形成字符…...
)
C# 事件(Event)
C# 事件(Event) C# 事件(Event)通过事件使用委托声明事件(Event)实例 C# 事件(Event) 事件(Event) 基本上说是一个用户操作,如按键、点击、鼠标移…...

2312d,d的sql构建器
原文 项目 该项目在我工作项目中广泛使用,它允许自动处理联接方式动态构建SQL语句. 还会自动直接按表示数据库行结构序化.它在dconf2022在线演讲中介绍了:建模一切. 刚刚添加了对sqlite的支持.该API还不稳定,但仍非常有用.这是按需构建,所以虽然有个计划外表,但满足了我的需要…...

以太网二层交换机实验
实验目的: (1)理解二层交换机的原理及工作方式; (2)利用交换机组建小型交换式局域网。 实验器材: Cisco packet 实验内容: 本实验可用一台主机去ping另一台主机,并…...

启封涂料行业ERP需求分析和方案分享
涂料制造业是一个庞大而繁荣的行业 它广泛用于建筑、汽车、电子、基础设施和消费品。涂料行业生产不同的涂料,如装饰涂料、工业涂料、汽车涂料和防护涂料。除此之外,对涂料出口的需求不断增长,这增加了增长和扩张的机会。近年来,…...
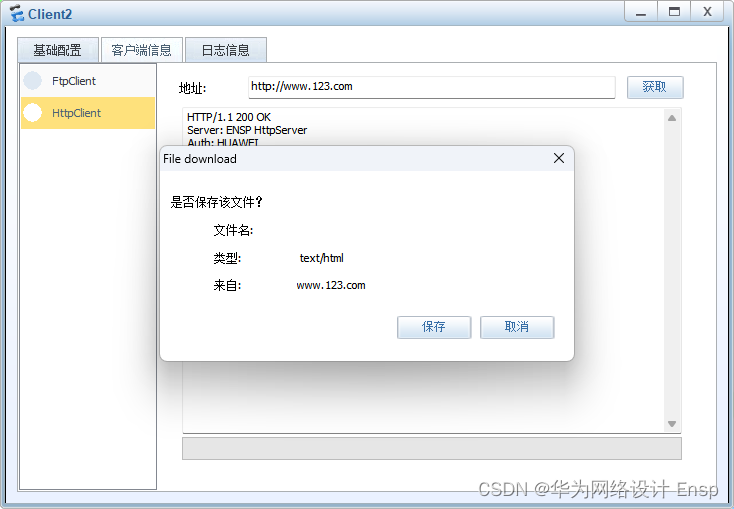
华为ensp网络设计期末测试题-复盘
网络拓扑图 地址分配表 vlan端口分配表 需求 The device is running!<Huawei>sys Enter system view, return user view with CtrlZ. [Huawei]un in en Info: Information center is disabled. [Huawei]sys S1 [S1]vlan 99 [S1-vlan99]vlan 100 [S1-vlan100]des IT [S1-…...

Dockerfile: WORKDIR vs VOLUME
WORKDIR WORKDIR指令为Dockerfile中的任何RUN、CMD、ENTRYPOINT、COPY和ADD指令设置工作目录。 如果WORKDIR不存在,它将被创建,即使它没有在任何后续Dockerfile指令中使用。 语法 : WORKDIR dirpath WORKDIR指令可以在Dockerfile中多次使用。如果提供了…...
;)
spring ioc源码-refresh();
主要作用是刷新应用上下文 Override public void refresh() throws BeansException, IllegalStateException {synchronized (this.startupShutdownMonitor) {// 启动刷新的性能跟踪步骤StartupStep contextRefresh this.applicationStartup.start("spring.context.refre…...

使用递归实现深拷贝
文章目录 为什么要使用递归什么深拷贝具体实现基础实现处理 函数处理 Symbol处理 Set处理 Map处理 循环引用 结语-源码 为什么要使用递归什么深拷贝 我们知道在 JavaScript 中可以通过使用JSON序列化来完成深拷贝,但是这种方法存在一些缺陷,比如对于函数…...

工程(十七)——自己数据集跑R2live
博主创建了一个科研互助群Q:772356582,欢迎大家加入讨论。 r2live是比较早的算法,编译过程有很多问题,通过以下两个博客可以解决 编译R2LIVE问题&解决方法-CSDN博客 r2live process has died 问题解决了_required process …...
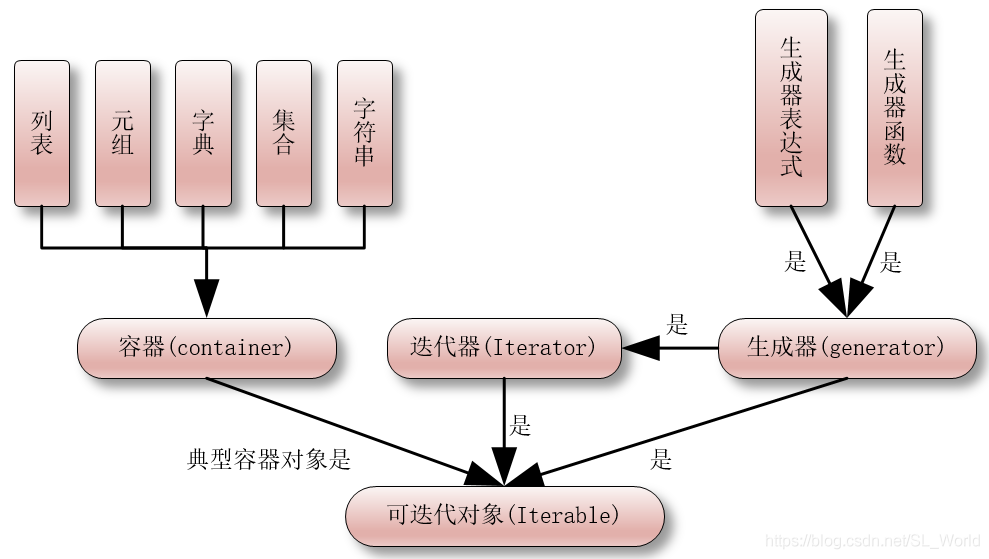
【python高级用法】迭代器、生成器、装饰器、闭包
迭代器 可迭代对象:可以使用for循环来遍历的,可以使用isinstance()来测试。 迭代器:同时实现了__iter__()方法和__next__()方法,可以使用isinstance()方法来测试是否是迭代器对象 from collections.abc import Iterable, Iterat…...

Nx市工业数据洞察:Flask、MySQL、Echarts的可视化之旅
Nx市工业数据洞察:Flask、MySQL、Echarts的可视化之旅 背景数据集来源技术选型功能介绍创新点总结 背景 随着工业化的不断发展,Nx市工业数据的收集和分析变得愈发重要。本博客将介绍如何利用Flask、MySQL和Echarts等技术,从统计局获取的数据…...

关于正态分布
目录 1.正态分布是什么2.正态分布有什么用途3.如何确定数据服从正态分布 本文简单介绍正态分布的基本概念和用途。 1.正态分布是什么 正态分布,也称为高斯分布,是由德国数学家卡尔弗里德里希高斯在研究测量误差时提出的。他发现许多自然现象和统计数据…...

每日一练(编程题-C/C++)
目录 CSDN每日一练1. 2023/2/27- 一维数组的最大子数组和(类型:数组 难度:中等)2. 2023/4/7 - 小艺照镜子(类型:字符串 难度:困难)3. 2023/4/14 - 最近的回文数(难度:中等)4. 2023/2/1-蛇形矩阵(难度:困难)…...

Unity UnityWebRequest 在Mac上使用报CommectionError
今天是想把前两天写的Demo拿到Mac上打个IPA的完事我发现 在运行时释放游戏资源的时候UnityWebRequest返回的结果不是Success 查看Log发现是 req.result 是CommectionError error是 Cannot connect to destination host 代码如下: UnityWebRequest req UnityWebRequ…...

WorkPlus为企业打造私有化部署IM解决方案
在移动数字化时代,企业面临着如何全面掌控业务和生态的挑战。企业微信、钉钉、飞书、Teams等应用虽然提供了部分解决方案,但无法满足企业的私有化部署需求。此时,WorkPlus作为安全专属的移动数字化平台,被誉为移动应用的“航空母舰…...
QT上位机开发(抽奖软件)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 用抽奖软件抽奖,是一种很常见的抽奖方式。特别是写这篇文章的时候,正好处于2023年12月31日,也是一年中最后一天…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...
