java的参数传递机制概述,方法重载概述,以及相关案例
前言:
学了Java的传递机制,稍微记录一下。循循渐进,daydayup!
java的参数传递机制概述
1,java的参数传递机制是什么?
java的参数传递机制是一种值传递机制。
2,值传递是什么?
值传递指的是,传输实参给方法形参的时候,实参存储的值的副本。
3,实参/形参是什么?
实参指的是在方法内部定义的变量。形参指的是方法定义时的变量。如下图:
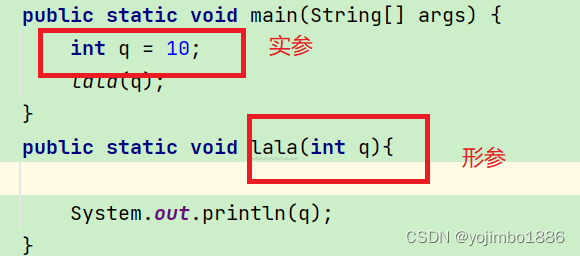
基本类型和引用类型的参数在传递时有什么不同?
1,基本类型的参数传递
基本类型的参数传递是一种值传递,参数储存的是数据值
例:如图代码
public static void main(String[] args) {int q =10;//laal(q);System.out.println("main"+q);}public static void laal(int q){System.out.println("一次"+ q);q = 20;System.out.println("二次"+ q);}结果如下:即使在方法里q赋值成了20,在main里q依旧输出10;

2,引用类型的参数传递
引用类型的参数传递同样是一种值传递,参数储存的是地址值
例:如图代码
public static void main(String[] args) {int [] lala = {1,2,3,4,5};la( lala);System.out.println("main"+lala [1]);}public static void la(int [] lala){System.out.println("第一次"+lala[1]);lala [1] = 20;System.out.println("第二次"+lala[1]);}结果如下:当方法中数组里的数改变后,main中也随之改变(因为参数记录的是地址值,并不影响引用数值的改变)

方法重载
1,什么是方法重载?
一个类中,多个方法的名称相同,但他们的形参列表不同
2,方法重载需要注意什么?
一个类中,只要一些方法的名称相同,形参列表不同(形参的个数,类型,顺序不同),那就是重载了
3,重载的应用场合是什么?
一类业务需要多种解决方案时(此时用方法重载特别专业)
例:如图代码
public static void lala(){}public static int lala(int a){ return a;}public static int lala(int a,int b){return a +b ;}
综合案例
案例1,用方法,把数组{1,2,3,4,5}按照[1|2|3|4|5]格式输出
public class definedemo3 {public static void main(String[] args) {int [] lol = {1,2,3,4,5};lala(lol);}public static void lala(int [] lol){if(lol == null){System.out.println("null");return;//以防是null}System.out.print("[");//添加[for (int i = 0; i < lol.length; i++) {//使数组循环输出System.out.print(i == lol.length - 1 ? lol[i]:lol[i]+"|");}//判断i是否等于数组最大长度,如果是则不输出|System.out.println("]");//加上]}
}实验结果:

案例2:两个数组对比,如果一致,输出true
实验思路:判断两个是否null;再判断两个长度是否一样;再判断两个数是否相同;
public static void main(String[] args) {int[] q1 = {1,2,3};int[] q2 = {1,2,3};System.out.println(lala(q1,q2));}public static boolean lala(int [] q1,int [] q2){if (q1 == null && q2 == null){return true;}if (q1 == null || q2 ==null){return false;}if (q1.length != q2.length){return false;}for (int i = 0; i < q1.length; i++) {if (q1[i] != q2[i]){return false;}}return true;}实验结果:实验成功,一致输出true,不一致输出false

案例3 :设计两个模式,模式1为发射导弹;模式2为向指定地区发射导弹
public class overloaddemo1 {public static void main(String[] args) {fire(1);fire("哈哈国",1);}public static void fire(int a){System.out.println(a);}public static void fire(String con,int a ){System.out.println("向"+con+"发射"+ a+"枚导弹");}
}实验结果:模式1为发射一枚导弹,模式2为向哈哈国发射1枚导弹

今日结束!
---------------------------------------------------------------------------------------------------------------------------------
最后
如果您看到了这篇文章,同时您也在学习java,希望您阅读这篇文章,希望与您一起讨论
基于黑马程序员的java学习笔记(持续更新)
相关文章:

java的参数传递机制概述,方法重载概述,以及相关案例
前言: 学了Java的传递机制,稍微记录一下。循循渐进,daydayup! java的参数传递机制概述 1,java的参数传递机制是什么? java的参数传递机制是一种值传递机制。 2,值传递是什么? 值…...

2013年第二届数学建模国际赛小美赛B题寄居蟹进化出人类的就业模式解题全过程文档及程序
2013年第二届数学建模国际赛小美赛 B题 寄居蟹进化出人类的就业模式 原题再现: 寄居蟹是美国最受欢迎的宠物品种,依靠其他动物的壳来保护。剥去寄居蟹的壳,你会看到它柔软、粉红色的腹部卷曲在头状的蕨类叶子后面。大多数寄居蟹喜欢蜗牛壳&…...

2023总结
随着各大应用程序开始发送自己的年终总结,我的2023也只剩最后的几个小时了 ,我的2023可以说是过的还算顺利,但是也算是一路坎坷,希望2024,我的本命年能够让我过的顺利点。 1,毕业进度 毕业进度总体来说还…...

Prometheus 监控进程
prometheus 进程的监控 1. process exporter功能 2. 监控目标对主机进程的监控,chronyd sshd 等服务进程已经已定义脚本运行程序的运行状态监控。 process-compose的安装 监控所有进程 mkdir /data/process_exporter -p cd /data/process_exporter创建配置文件 …...

用ChatGPT挑选钻石!著名珠宝商推出-珠宝GPT
根据Salesforce最新发布的第五版《互联网购物报告》显示,ChatGPT等生成式AI的出现、快速发展,对零售行业和购物者产生了较大影响。可有效简化业务流程实现降本增效,并改善购物体验。 著名珠宝商James Allen为了积极拥抱生成式AI全面提升销售…...
啊?这也算事务?!
作者简介:大家好,我是smart哥,前中兴通讯、美团架构师,现某互联网公司CTO 联系qq:184480602,加我进群,大家一起学习,一起进步,一起对抗互联网寒冬 学习必须往深处挖&…...
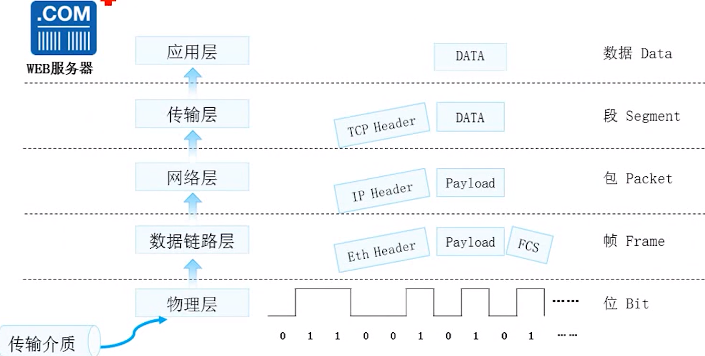
数据通信网络基础的网络参考模型华为ICT网络赛道
网络参考模型 目录 网络参考模型 2.1.应用与数据 2.2.网络参考模型与标准协议 2.2.1.OSI参考模型 2.2.2.TCP/IP参考模型 2.2.3.应用层 2.2.4.传输层 2.2.5.TCP和UDP 2.2.6.网络层 2.2.7.数据链路层 2.2.8.物理层 2.3.数据通信过程 2.1.应用与数据 应用的存在&#…...
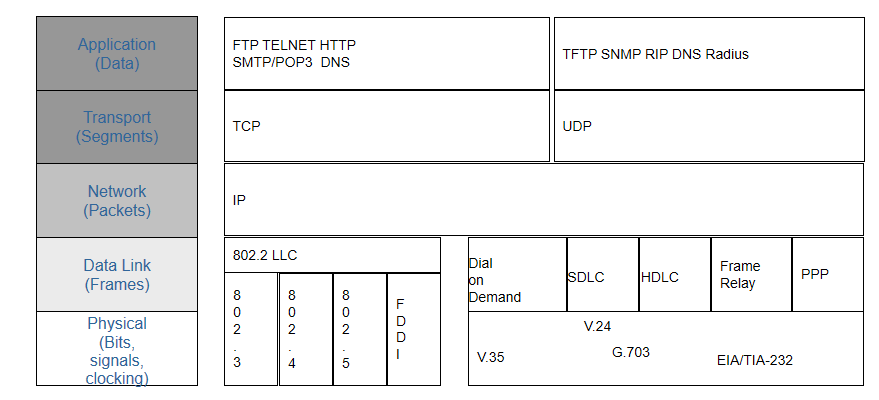
弱电工程计算机网络系统基础知识
我们周围无时无刻不存在一张网,如电话网、电报网、电视网、计算机网络等;即使我们身体内部也存在许许多多的网络系统,如神经系统、消化系统等。最为典型的代表即计算机网络,它是计算机技术与通信技术两个领域的结合。 计算机网络的…...
大数据与人工智能|万物皆算法(第三节)
要点一:数据与智能的关系 1. 一切的核心都是数据,数据和智能之间是密切相关的。 数据是对客观现实的描述,而信息是数据转化而来的。 例如,24是数据,但说“今天的气温是24摄氏度”是信息,而说“班可以分成24…...

[语音识别]开源语音识别faster-whisper模型下载地址
官方源码: https://github.com/SYSTRAN/faster-whisper 模型下载地址: large-v3模型:https://huggingface.co/Systran/faster-whisper-large-v3/tree/main large-v2模型:https://huggingface.co/guillaumekln/faster-whisper-l…...
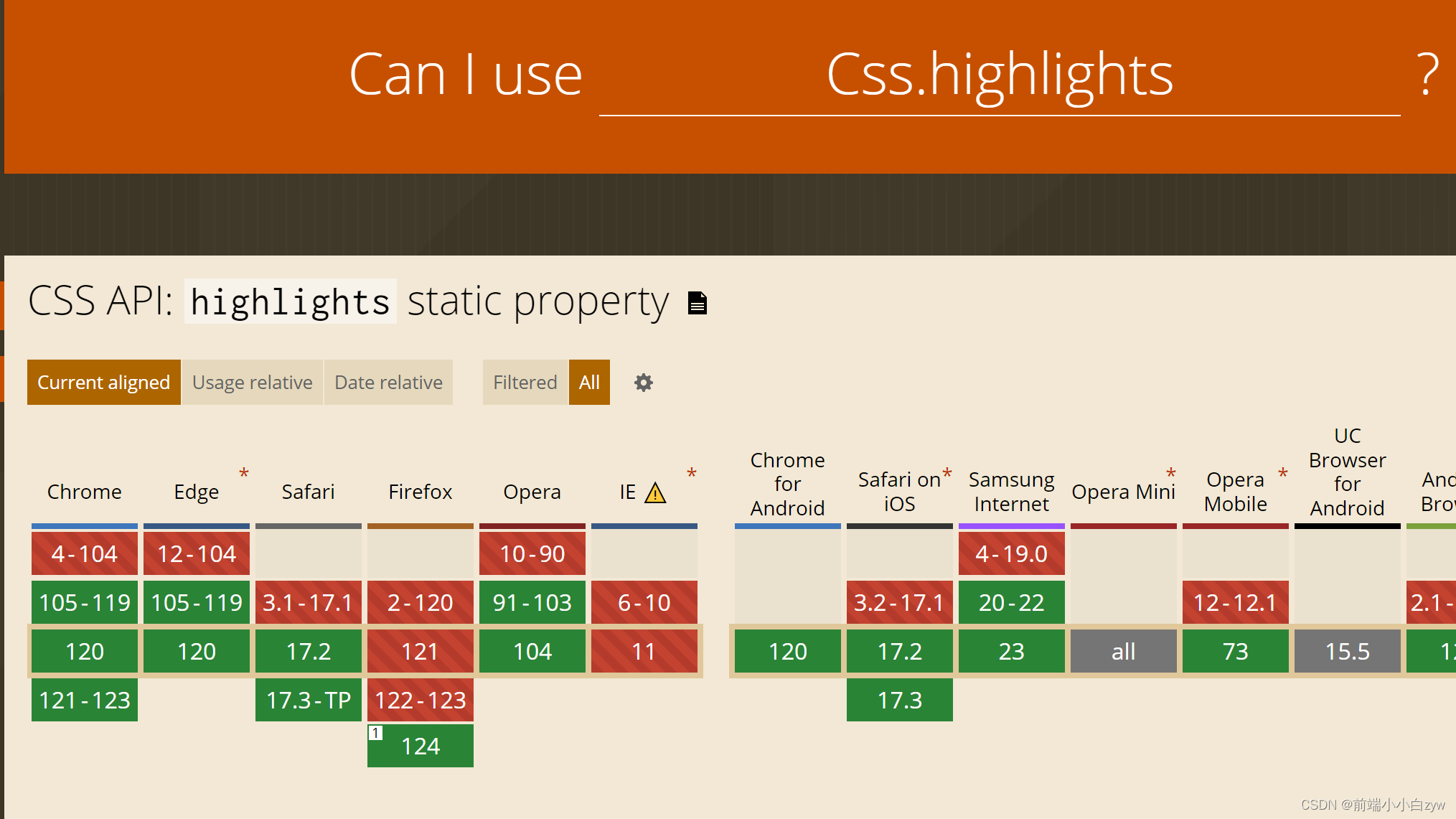
JS + CSS 实现高亮关键词(不侵入DOM)
之前在做关键词检索高亮功能的时候,研究了下目前前端实现高亮的几种方式,第一就是替换dom元素实现高亮,第二就是利用浏览器新特性Css.highlights结合js选区与光标与CSS高亮伪类实现,实现功能如下: 一、页面布局 一个…...
Qt 中使用 MySQL 数据库保姆级教程(下)
作者:billy 版权声明:著作权归作者所有,商业转载请联系作者获得授权,非商业转载请注明出处 前言 上篇中我们安装好了 MySQL 数据库和 Navicat 软件,下面在 Qt 中尝试使用数据库 1. 在 Qt 中连接 MySQL 数据库&#…...
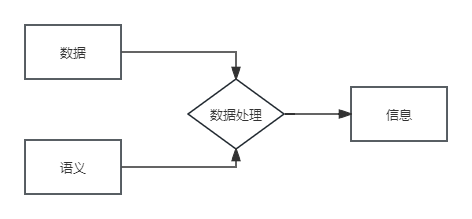
【数据库原理】(1)数据库技术的发展
数据与信息 数据:数据并非只是数字,像文字、符号、图像、影音等都属于数据的范畴。但一般会用数字来表述客观事物的数量、质量、关系等,便于更加直观的看待问题。 语义:数据还需要结合关联的语义解释才能够清晰的描述事物&#…...

【动态规划】【字符串】C++算法:正则表达式匹配
作者推荐 视频算法专题 涉及知识点 动态规划 字符串 LeetCode10:正则表达式匹配 给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 ‘.’ 和 ‘’ 的正则表达式匹配。 ‘.’ 匹配任意单个字符 ’ 匹配零个或多个前面的那一个元素 所谓匹配,是…...

fgetc_fgets_getc_getchar
一、fgetc 1、从流中读取下一个字符 下一个的意思是紧跟在指针后面的,对于一个刚打开文件的流,指针在文件的最前面,它的下一个字符就是文件的第一个字符。读完第一个字符后,指针就会走到第一个字符后面,这时它的下一个…...
12.30_黑马数据结构与算法笔记Java
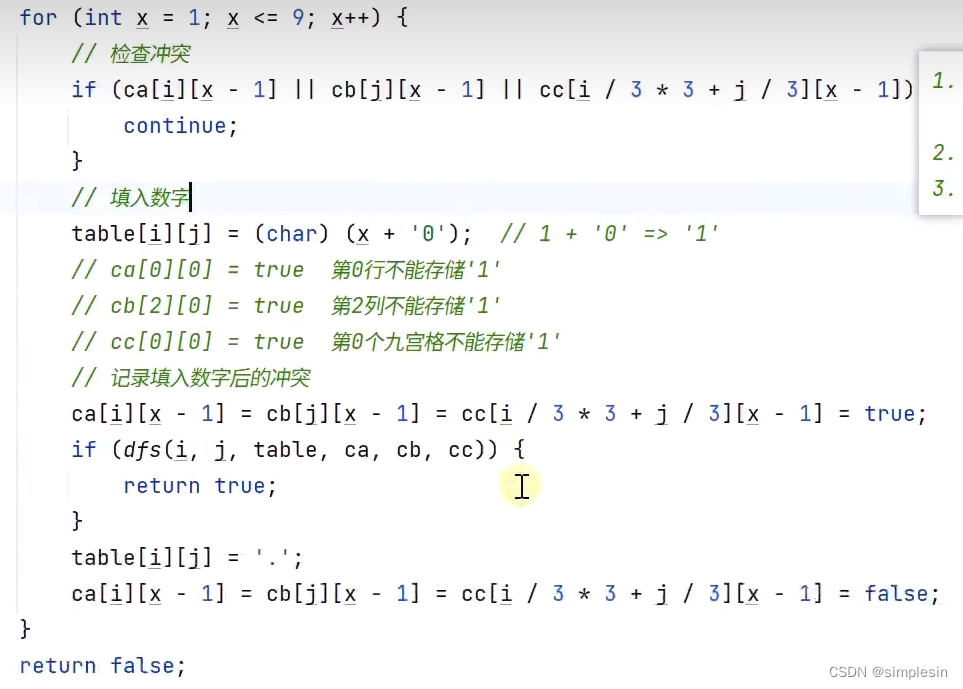
目录 320 全排列无重复 Leetcode47 321 组合 Leetcode77 分析 322 组合 Leetcode77 实现 323 组合 Leetcode77 剪枝 324 组合之和 Leetcode 39 325 组合之和 Leetcode 40 326 组合之和 Leetcode 216 327 N皇后 Leetcode51-1 328 N皇后 Leetcode51-2 329 解数独 Leetco…...

【电路笔记】-电容分压器
电容分压器 文章目录 电容分压器1、概述2、串联电容器的电压分布3、电容分压器示例14、电容分压器示例2 分压器电路可以由电抗元件构成,就像由固定值电阻器构成一样容易。 1、概述 但就像电阻电路一样,电容分压器网络即使使用属于电抗元件的电容器&…...

线性代数基础知识
计算机视觉一些算法中常会用到线性代数的一些知识,为了便于理解和快速回忆,博主这边对常用的一些知识点做下整理,主要来源于如下这本书籍。 1. 矩阵不仅仅是数字排列而已,不然也不会有那么大精力研究它。其可以表示一种映射 关于…...

Linux Shell 016-文本比较工具diff
Linux Shell 016-文本比较工具diff 本节关键字:Linux、Bash Shell、文本比较 相关指令:diff、cat、patch diff介绍 diff工具用于逐行比较文件的不同,如果指定要比较目录,则diff会比较目录中相同文件名的文件,但不会…...
)
八股文打卡day13——计算机网络(13)
面试题:DNS是什么?DNS的查询过程是什么? 我的回答: 我来讲一下我对DNS的理解 DNS是域名系统,它是一个域名和IP地址相互映射的数据库。通过DNS,可以将我们浏览器中输入的域名,例如:…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...
