图文证明 费马,罗尔,拉格朗日,柯西
图文证明 罗尔,拉格朗日,柯西
费马引理和罗尔都比较好证,不过多阐述,看图即可:
费马引理:
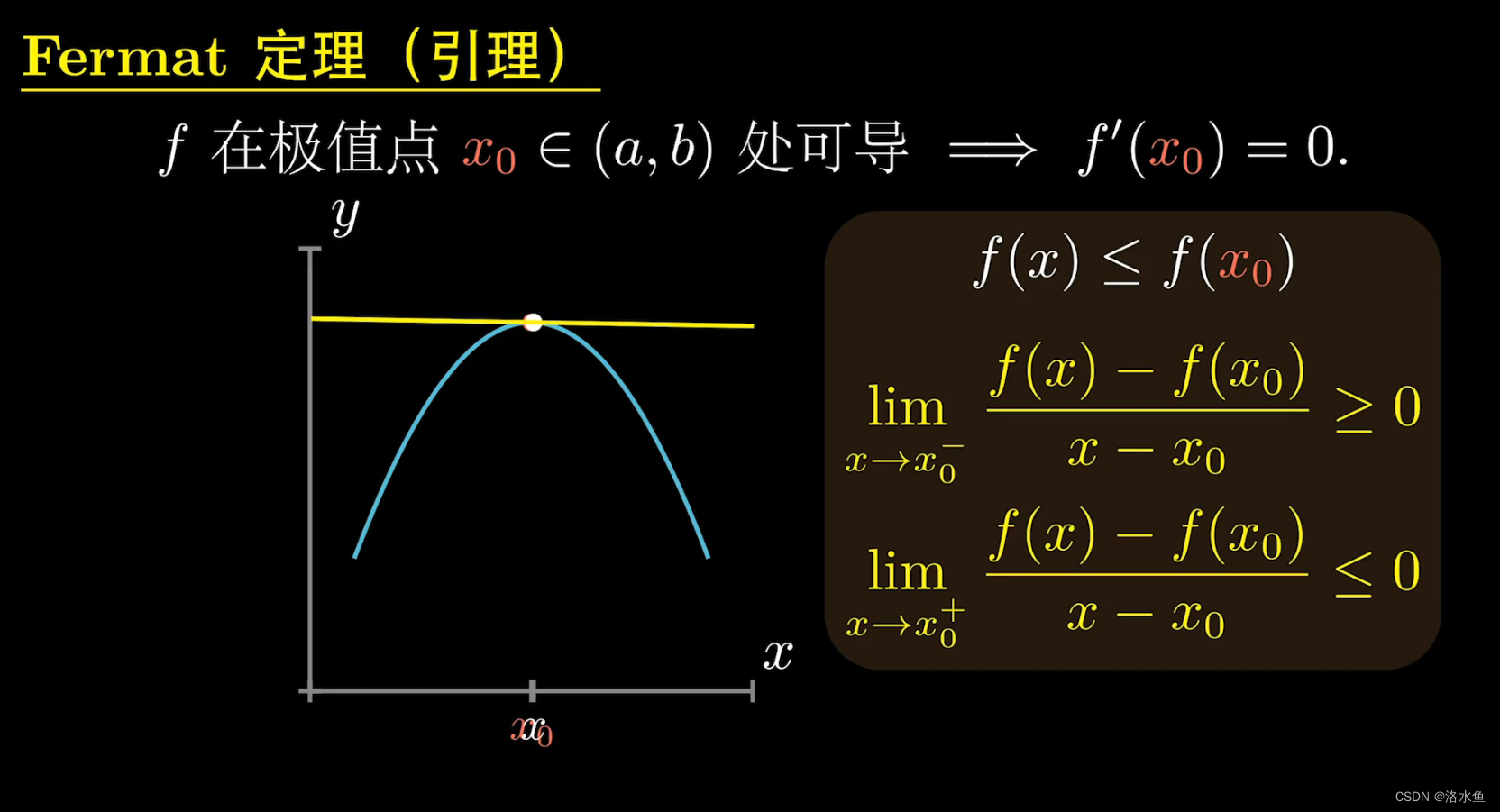
罗尔定理:

重点来证明拉格朗日和柯西
拉格朗日:

我认为不需要去看l(x)的那一行更好推:
详细的推理过程:
构造 h ( x ) = f ( x ) − l ( x ) , 因为 a , b 两点为交点 , f ( a ) = l ( a ) , f ( b ) = l ( b ) , 构造h(x) = f(x) - l(x), \quad \text{因为} \; a, b \; \text{两点为交点}, \; f(a) = l(a), \; f(b) = l(b), 构造h(x)=f(x)−l(x),因为a,b两点为交点,f(a)=l(a),f(b)=l(b),
所以 h ( a ) = h ( b ) = 0. 根据罗尔定理 , ∃ c ∈ ( a , b ) 使得 h ′ ( ξ ) = 0. \text{所以} \; h(a) = h(b) = 0. \quad \text{根据罗尔定理}, \; \exists \, c \in (a, b) \; \text{使得} \; h'(\xi ) = 0. 所以h(a)=h(b)=0.根据罗尔定理,∃c∈(a,b)使得h′(ξ)=0.
因为 h ( ξ ) = f ( ξ ) − l ( ξ ) , 我们有 h ′ ( ξ ) = f ′ ( ξ ) − l ′ ( ξ ) . 因此 , h ′ ( ξ ) = f ′ ( ξ ) − l ′ ( ξ ) = 0. \text{因为} \; h(\xi ) = f(\xi ) - l(\xi ), \; \text{我们有} \; h'(\xi ) = f'(\xi ) - l'(\xi ). \quad \text{因此}, \; h'(\xi ) = f'(\xi ) - l'(\xi ) = 0. 因为h(ξ)=f(ξ)−l(ξ),我们有h′(ξ)=f′(ξ)−l′(ξ).因此,h′(ξ)=f′(ξ)−l′(ξ)=0.
由此得出 f ′ ( ξ ) = l ′ ( ξ ) . \text{由此得出} \; f'(\xi ) = l'(\xi ). 由此得出f′(ξ)=l′(ξ).
根据两点式得: l ′ ( ξ ) = f ( b ) − f ( a ) b − a \text{根据两点式得:} \; l'(\xi ) = \frac{{f(b)-f(a)}}{{b-a}} 根据两点式得:l′(ξ)=b−af(b)−f(a)
由于已知 f ′ ( ξ ) = l ′ ( ξ ) , 你可以使用这个信息进一步推导出 f ′ ( x ) = l ′ ( x ) = f ( b ) − f ( a ) b − a . \text{由于已知} \; f'(\xi ) = l'(\xi ), \; \text{你可以使用这个信息进一步推导出} \; \ f'(x) = l'(x) = \frac{{f(b)-f(a)}}{{b-a}}. 由于已知f′(ξ)=l′(ξ),你可以使用这个信息进一步推导出 f′(x)=l′(x)=b−af(b)−f(a).
柯西:

给定两个函数 f ( x ) 和 g ( x ) \text{给定两个函数} \; f(x) \; \text{和} \; g(x) \; 给定两个函数f(x)和g(x)
在区间 [ a , b ] 上,其中 f ( x ) ≠ g ( x ) 。根据拉格朗日中值定理,存在 c ∈ ( a , b ) 使得 \text{在区间} \; [a, b] \; \text{上,其中} \; f(x) \neq g(x) \; \text{。根据拉格朗日中值定理,存在} \; c \in (a, b) \; \text{使得} 在区间[a,b]上,其中f(x)=g(x)。根据拉格朗日中值定理,存在c∈(a,b)使得
f ′ ( ξ ) = f ( b ) − f ( a ) b − a , g ′ ( ξ ) = g ( b ) − g ( a ) b − a . f'(\xi ) = \frac{f(b) - f(a)}{b - a}, \quad g'(\xi ) = \frac{g(b) - g(a)}{b - a}. f′(ξ)=b−af(b)−f(a),g′(ξ)=b−ag(b)−g(a).
现在,我们使用换元法,将 f ′ ( ξ ) 的 ( b − a ) 替换为 g ( b ) − g ( a ) g ′ ( ξ ) \text{现在,我们使用换元法,将} \; f'(\xi ) \; \text{的} \; (b - a) \; \text{替换为} \; \frac{g(b) - g(a)}{g'(\xi )} 现在,我们使用换元法,将f′(ξ)的(b−a)替换为g′(ξ)g(b)−g(a)
f ′ ( c ) = f ( b ) − f ( a ) g ( b ) − g ( a ) g ′ ( c ) . f'(c) = \frac{f(b) - f(a)}{\frac{g(b) - g(a)}{g'(c)}}. f′(c)=g′(c)g(b)−g(a)f(b)−f(a).
通过简化得到 f ′ ( c ) = f ( b ) − f ( a ) g ( b ) − g ( a ) ⋅ g ′ ( c ) . \text{通过简化得到} \; f'(c) = \frac{f(b) - f(a)}{g(b) - g(a)} \cdot g'(c). 通过简化得到f′(c)=g(b)−g(a)f(b)−f(a)⋅g′(c).
发现一个看一眼就明了的列子
拉格朗日:如果你一小时跑了5km,你的平均速度就是5km/h。那么在这一小时以内,要么一直保持5km/h,要么一部分比这个速度快,一部分比这个速度慢。在快慢转换的点,你的速度就是5km/h。
柯西:我一小时跑了5km,你一小时跑了20km。要么你的速度一直是我的20/5=4倍,要么你一部分比我四倍还快,一部分比我四倍慢,在这转换的这一点,你的速度是我的四倍。
参考视频:
罗尔、拉格朗日、柯西【中值定理】 证明
相关文章:

图文证明 费马,罗尔,拉格朗日,柯西
图文证明 罗尔,拉格朗日,柯西 费马引理和罗尔都比较好证,不过多阐述,看图即可: 费马引理: 罗尔定理: 重点来证明拉格朗日和柯西 拉格朗日: 我认为不需要去看l(x)的那一行更好推: 详细的推理过程: 构造 h ( x ) f ( x ) − l ( x ) , 因为 a , b 两点为交点 , f ( a ) l ( …...
CEC2017(Python):粒子群优化算法PSO求解CEC2017(提供Python代码)
一、CEC2017简介 参考文献: [1]Awad, N. H., Ali, M. Z., Liang, J. J., Qu, B. Y., & Suganthan, P. N. (2016). “Problem definitions and evaluation criteria for the CEC2017 special session and competition on single objective real-parameter numer…...
(一))
AUTOSAR从入门到精通- 虚拟功能总线(RTE)(一)
目录 前言 几个高频面试题目 RTE S/R接口implicit与Explicit的实现与区别 接口的代码 implicit...

B/S架构云端SaaS服务的医院云HIS系统源码,自主研发,支持电子病历4级
医院云HIS系统源码,自主研发,自主版权,电子病历病历4级 系统概述: 一款满足基层医院各类业务需要的云HIS系统。该系统能帮助基层医院完成日常各类业务,提供病患挂号支持、病患问诊、电子病历、开药发药、会员管理、统…...
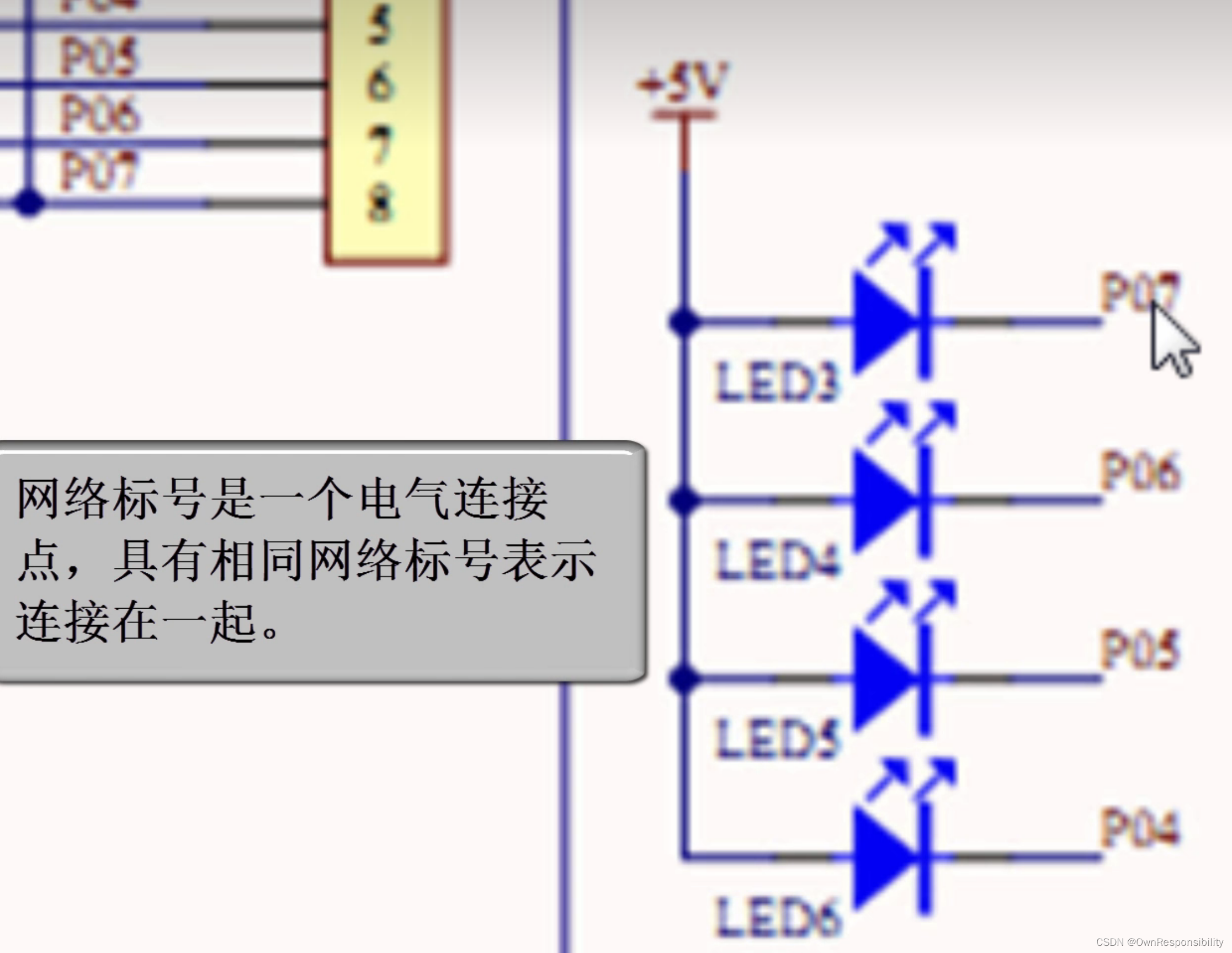
看懂基本的电路原理图(入门)
文章目录 前言一、二极管二、电容三、接地一般符号四、晶体振荡器五、各种符号的含义六、查看原理图的顺序总结 前言 电子入门,怎么看原理图,各个图标都代表什么含义,今天好好来汇总一下。 就比如这个电路原理图来说,各个符号都…...

赫夫曼树基本数据结构
自编头文件: #ifndef HUFFMAN_H_INCLUDED #define HUFFMAN_H_INCLUDED#include<limits.h> #include<string.h> typedef struct {unsigned int weight;unsigned int parent,lchild,rchild; }HTNode,*HuffmanTree; typedef char** HuffmanCode;void Sele…...
10TB海量JSON数据从OSS迁移至MaxCompute
前提条件 开通MaxCompute。 在DataWorks上完成创建业务流程,本例使用DataWorks简单模式。详情请参见创建业务流程。 将JSON文件重命名为后缀为.txt的文件,并上传至OSS。本文中OSS Bucket地域为华东2(上海)。示例文件如下。 {&qu…...
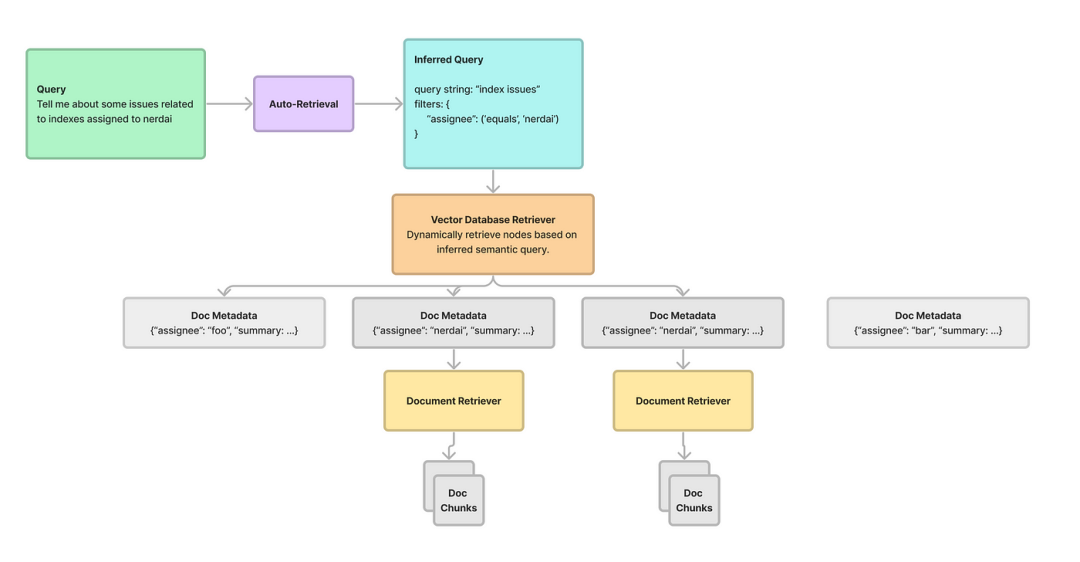
LLM之RAG实战(九)| 高级RAG 03:多文档RAG体系结构
在RAG(检索和生成)这样的框架内管理和处理多个文档有很大的挑战。关键不仅在于提取相关内容,还在于选择包含用户查询所寻求的信息的适当文档。基于用户查询对齐的多粒度特性,需要动态选择文档,本文将介绍结构化层次检索…...

Windows电脑引导损坏?按照这个教程能修复
前言 Windows系统的引导一般情况下是不会坏的,小伙伴们可以不用担心。发布这个帖子是因为要给接下来的文章做点铺垫。 关注小白很久的小伙伴应该都知道,小白的文章都讲得比较细。而且文章与文章之间的关联度其实还是蛮高的。在文章中,你会遇…...

记Android字符串资源支持的参数类型
参数以%开头,后拼接对应的参数类型名称,如下所示: <string name"tips">Hello, %s! You have some new messages.</string> 类型名称如下所示: s字符串格式用于插入字符串值。例如,"Hel…...
Java实现树结构(为前端实现级联菜单或者是下拉菜单接口)
Java实现树结构(为前端实现级联菜单或者是下拉菜单接口) 我们常常会遇到这样一个问题,就是前端要实现的样式是一个级联菜单或者是下拉树,如图 这样的数据接口是怎么实现的呢,是什么样子的呢? 我们可以看看 …...

MySQL中常用的数据类型
整型 int 有符号范围: -2147483648 ~ 2147483647 int unsigned 无符号范围: 0 ~ 4294967295 int(5) zerofill 仅用于显示,当不满足5位时,按照左边补0,例如: 00002满足时,正常显示 tinyint[(m)] [unsigned] [zerofill] 有符号&a…...

HTML+CSS+JS制作三款雪花酷炫特效
🎀效果展示 🎀代码展示 <!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd"> <html...
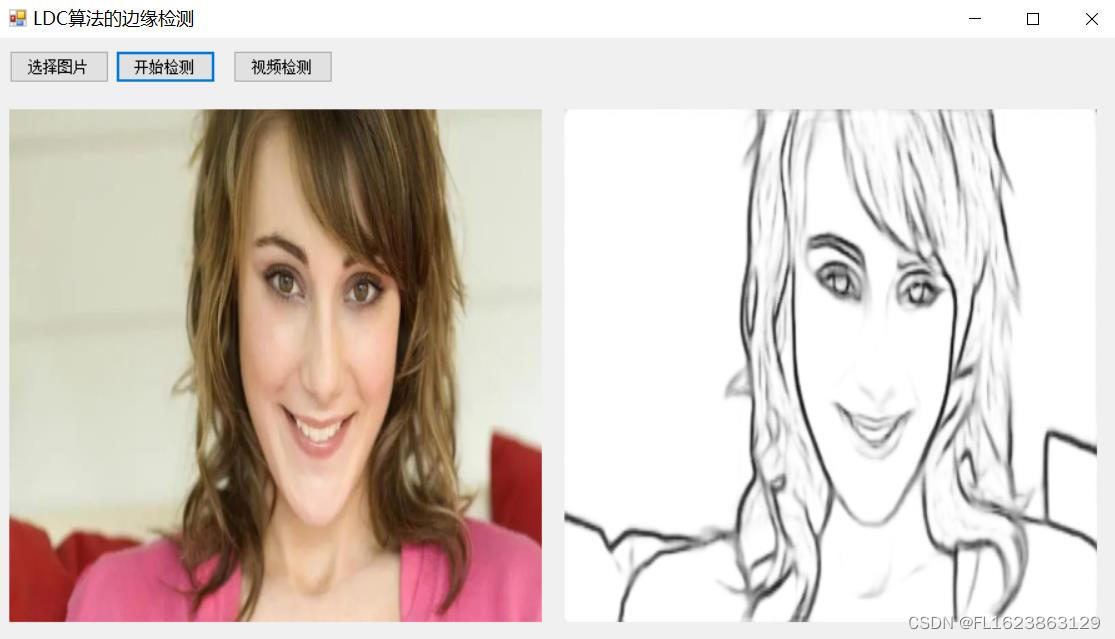
[C#]使用ONNXRuntime部署一种用于边缘检测的轻量级密集卷积神经网络LDC
源码地址: github.com/xavysp/LDC LDC: Lightweight Dense CNN for Edge Detection算法介绍: 由于深度学习方法的快速发展,近年来,用于执行图像边缘检测的卷积神经网络(CNN)模型爆炸性地传播。但边缘检测…...

ZigBee案例笔记 - 无线点灯
文章目录 无线点灯实验概述工程关键字工程文件夹介绍Basic RF软件设计框图简单说明工程操作Basic RF启动流程Basic RF发送流程Basic RF接收流程 无线点灯案例无线点灯现象 无线点灯实验概述 ZigBee无线点灯实验(即Basic RF工程),由TI公司提供…...
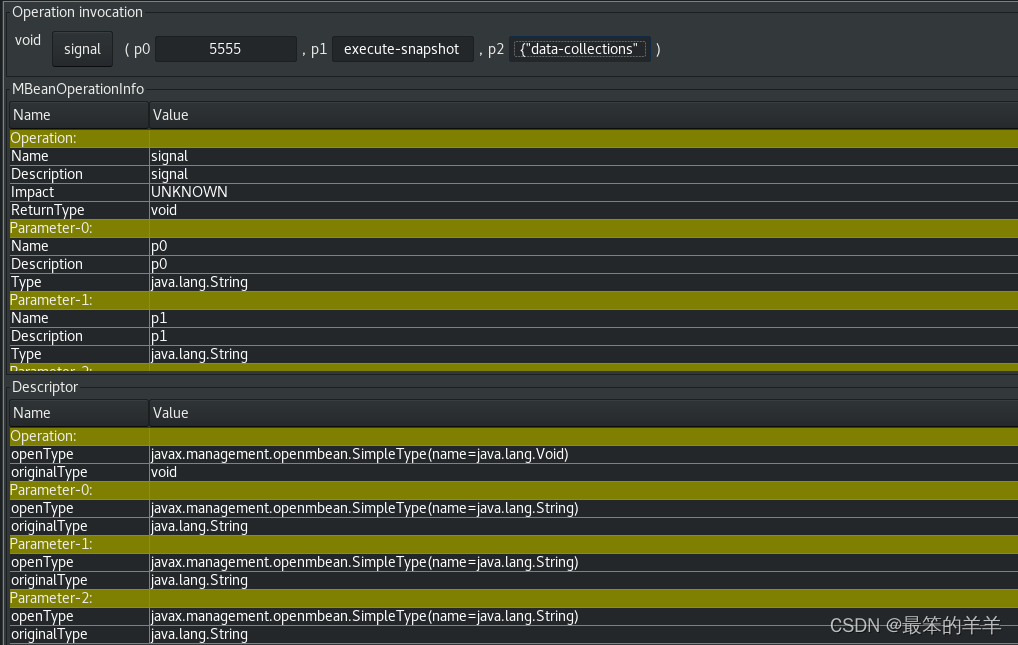
Debezium日常分享系列之:向 Debezium 连接器发送信号
Debezium日常分享系列之:向 Debezium 连接器发送信号 一、概述二、激活源信号通道三、信令数据集合的结构四、创建信令数据集合五、激活kafka信号通道六、数据格式七、激活JMX信号通道八、自定义信令通道九、Debezium 核心模块依赖项十、部署自定义信令通道十一、信…...

《C#程序设计教程》总复习
一、单项选择题 1.short 类型的变量在内存中占据的位数是 ( )。 A. 8 B. 16 C. 32 D. 64 2.对千 int[ 4,5]型的数组 a, 数组元素 a[2,3] 存在数组第 ( )个位置上。 A. 11 B. 12 C. 14 D. 15 3.设 int 类型变量 x,y,z 的值分别是2、3、6 , 那么…...

为什么ChatGPT选择了SSE,而不是WebSocket?
我在探索ChatGPT的使用过程中,发现了一个有趣的现象:ChatGPT在实现流式返回的时候,选择了SSE(Server-Sent Events),而非WebSocket。 那么问题来了:为什么ChatGPT选择了SSE,而不是We…...
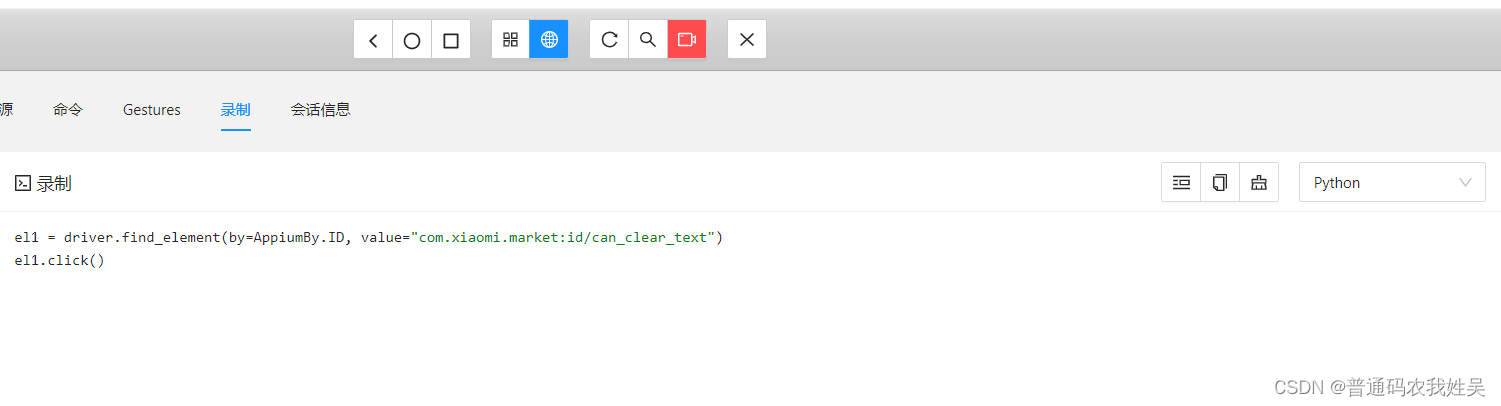
appium入门基础
介绍 appium支持在不同平台的UI自动化,如web,移动端,桌面端等。还支持使用java,python,js等语言编写自动化代码。主要用于自动化测试脚本,省去重复的手动操作。 Appium官网 安装 首先必须环境有Node.js用于安装Appium。 总体来…...
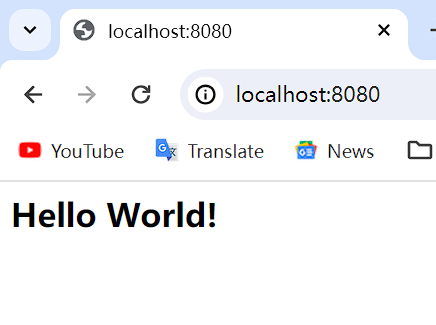
jsp介绍
JSP 一种编写动态网页的语言,可以嵌入java代码和html代码,其底层本质上为servlet,html部分为输出流,编译为java文件 例如 源jsp文件 <% page contentType"text/html; charsetutf-8" language"java" pageEncoding&…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...
