从有向带权图判断最短路径里各目标顶点顺序
对如下有向带权图,若采用迪杰斯特拉(Dijkstra)算法求从源点a到其他各顶点的最短路径,则得到的第一路径的目标顶点是b,第二条最短路径的目标顶点是c,后续得到的其余各最短路径的目标顶点依次是()
A.d,e,f
B.e,d,f
C.f,d,e
D.f,e,d

首先,先看除了a还有5个顶点,那么就是要走5趟。
在下面表格列出b、c、d、e、f 以及一两三四五趟,最后一行写集合。
| 顶点 | 一趟 | 两趟 | 三趟 | 四趟 | 五趟 |
| b | |||||
| c | |||||
| d | |||||
| e | |||||
| f | |||||
| 集合 |

- 在一开始我自己定义:
- 顶点a至b算一趟,顶点a至c也算一趟
- 以此类推,例如后面讲述的顶点a至b至c算两趟
- 然后再看,从a出发,首先接触的是b、c,那么分别写下到b和c的距离。
- 其他顶点对a来说一趟接触不到,那么我们就写无穷,即∞。
- 其中,(a,b)最短,距离为2,那么得出结论:集合就是{a,b}
- 由于顶点c这次没被引用,于是将(a,c)5先搁置至二趟(但每一次搁置到后面一趟需检验a至c是不是最短的,还有没有从a至c更加短的距离,详情看后面几轮)
| 顶点 | 一趟 | 两趟 | 三趟 | 四趟 | 五趟 |
| b | (a,b)2 | ||||
| c | (a,c)5 | (a,c)5 | |||
| d | ∞ | ||||
| e | ∞ | ||||
| f | ∞ | ||||
| 集合 | {a,b} |

- 然后再看,从a至b出发,能走两趟的就只有(a,b,c)和(a,b,d),此时(a,b,c)距离为3,(a,b,d)距离为5。
- 上一趟的(a,c)搁置到二趟需检验a至c是不是最短的,还有没有从a至c更加短的路线,哦有,就是我们刚才写的(a,b,c),(a,c)距离为5,(a,b,c)距离才3,那么就用(a,b,c)代替(a,c)。
- 此时(a,b,c)距离为3,(a,b,d)距离为5
- 那么最短的就是(a,b,c)
- 那么集合就是{a,b,c}
| 顶点 | 一趟 | 两趟 | 三趟 | 四趟 | 五趟 |
| b | (a,b)2 | ||||
| c | (a,c)5 | (a,c)5/(a,b,c)3 | |||
| d | ∞ | (a,b,d)5 | |||
| e | ∞ | ∞ | |||
| f | ∞ | ∞ | |||
| 集合 | {a,b} | {a,b,c} |

- 然后再看,此时b和c都被引用了,就剩d、e、f,即从a至b至c出发,能走三趟的,能接触到的就是d、e、f
- 此时三趟为(a,b,c,d)距离为6,(a,b,c,e)距离为7,(a,b,c,f)距离为4。
- (a,b,d)因为上一趟距离长没有选上,虽不是最短,但可以先搁置到这一趟继续写,但搁置到这一趟需检验a至d是不是最短的,还有没有从a至d更加短的路线,哦没有,还是(a,b,d),(a,b,c,d)距离为6,(a,b,d)距离才5,那么就保留(a,b,d)。
- 此时三趟为(a,b,d)距离为5,(a,b,c,e)距离为7,(a,b,c,f)距离为4,(a,b,c,f)最短,选(a,b,c,f)。
- 故集合为{a,b,c,f}
| 顶点 | 一趟 | 两趟 | 三趟 | 四趟 | 五趟 |
| b | (a,b)2 | ||||
| c | (a,c)5 | (a,c)5/(a,b,c)3 | |||
| d | ∞ | (a,b,d)5 | (a,b,d)5/(a,b,c,d)6 | ||
| e | ∞ | ∞ | (a,b,c,e)7 | ||
| f | ∞ | ∞ | (a,b,c,f)4 | ||
| 集合 | {a,b} | {a,b,c} | {a,b,c,f} |

- 然后再看,从a至b至c至f出发,能走四趟的,能接触到的就是d、e
- (a,b,d)是从二趟开始搁置到这一趟,因为已经检验过了所以不用检验,而(a,b,c,e)是从三趟才开始搁置的,还没检验过,检验一下,(a,b,c,e)距离为7,(a,b,d,e)距离为6,(a,c,e)距离为9,(a,b,c,d,e)距离为7,故(a,b,d,e)最短,用(a,b,d,e)替代这几个
- 然而虽然(a,b,d,e)距离为6,(a,b,d)5距离为5而已,故还是选(a,b,d)。
- 故集合为{a,b,c,f,d}
| 顶点 | 一趟 | 两趟 | 三趟 | 四趟 | 五趟 |
| b | (a,b)2 | ||||
| c | (a,c)5 | (a,c)5/(a,b,c)3 | |||
| d | ∞ | (a,b,d)5 | (a,b,d)5/(a,b,c,d)6 | (a,b,d)5 | |
| e | ∞ | ∞ | (a,b,c,e)7 | (a,b,c,e)7/(a,b,d,e)6/(a,c,e)9/(a,b,c,d,e)7 | |
| f | ∞ | ∞ | (a,b,c,f)4 | ||
| 集合 | {a,b} | {a,b,c} | {a,b,c,f} | {a,b,c,f,d} |

- 然后再看,此时就剩e,即从a至b至c至f至d出发,能走五趟的,能接触到的就只有e了
- (a,b,d,e)是从四趟开始搁置到这一趟,因为已经检验过了所以不用检验。
- 故集合为{a,b,c,f,d,e}
| 顶点 | 一趟 | 两趟 | 三趟 | 四趟 | 五趟 |
| b | (a,b)2 | ||||
| c | (a,c)5 | (a,c)5/(a,b,c)3 | |||
| d | ∞ | (a,b,d)5 | (a,b,d)5/(a,b,c,d)6 | (a,b,d)5 | |
| e | ∞ | ∞ | (a,b,c,e)7 | (a,b,c,e)7/(a,b,d,e)6/(a,c,e)9/(a,b,c,d,e)7 | (a,b,d,e)6 |
| f | ∞ | ∞ | (a,b,c,f)4 | ||
| 集合 | {a,b} | {a,b,c} | {a,b,c,f} | {a,b,c,f,d} | {a,b,c,f,d,e} |
故后续得到的其余各最短路径的目标顶点依次是{a,b,c,f,d,e}
相关文章:

从有向带权图判断最短路径里各目标顶点顺序
对如下有向带权图,若采用迪杰斯特拉(Dijkstra)算法求从源点a到其他各顶点的最短路径,则得到的第一路径的目标顶点是b,第二条最短路径的目标顶点是c,后续得到的其余各最短路径的目标顶点依次是() A.d,e,f B.e,d,f C.f,d,e D.f,…...

鼠标驱动框架:模拟键盘按键
/* 参考: drivers\hid\usbhid\usbmouse.c */ #include <linux/kernel.h> #include <linux/slab.h> #include <linux/module.h> #include <linux/init.h> #include <linux/usb.h> #include <linux/input.h> #include <linux/hid.h>st…...
ES6之Promise的链式调用
✨ 专栏介绍 在现代Web开发中,JavaScript已经成为了不可或缺的一部分。它不仅可以为网页增加交互性和动态性,还可以在后端开发中使用Node.js构建高效的服务器端应用程序。作为一种灵活且易学的脚本语言,JavaScript具有广泛的应用场景&#x…...
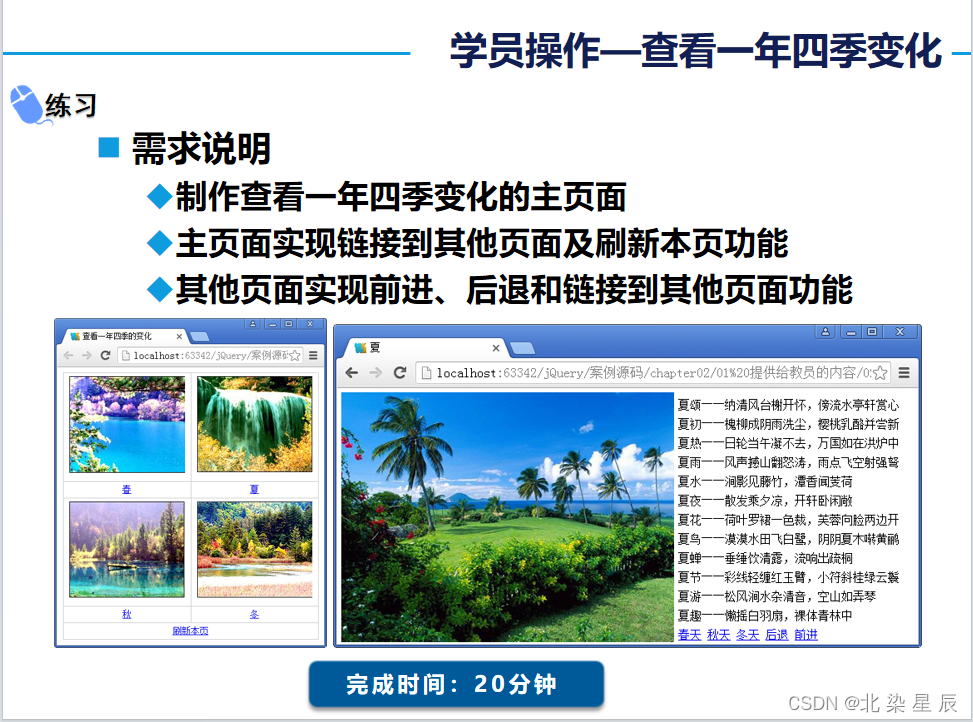
HTML----JavaScript操作对象BOM对象
文章目录 目录 文章目录 本章要求 一.BOM模型概述 二.BOM核心:window对象 常用属性 常用方法: confirm() 案例 open ()close()案例 setTimeout( ) 案例 setInterval( ) 案例 document对象 练习 本章要求 了解BOM模型掌握BOM模型实际应用 一.BOM模型…...
)
隆道数智大会回顾|第13期《如何构建绿色产业供应链新生态》(完)
本期演讲嘉宾: 史文月 采购与供应链专家 邢庆峰 品类管理和质量管理专家 刘婷婷 中兴通讯供应链规划总监 张燕华 正大生物CIO 吴树贵 隆道公司总裁 本期演讲主题: 如何构建绿色产业供应链新生态 本期内容要点: 1.供应链管理的核心问…...
粒子群优化pso结合bp神经网络优化对csv文件预测matlab(3)
1.csv数据为密西西比数据集,获取数据集可以管我要,数据集内容形式如下图: 2.代码 这里参考的是b站的一位博主。 数据集导入教程在我的另一篇文章bp写过,需要的话可以去看一下 psobp.m close all clc%读取数据 inputX; outputY;…...

软性演员-评论家算法 SAC
软性演员-评论家算法 SAC 软性演员-评论家算法 SAC优势原理软性选择模型结构目标函数重参数化熵正则化代码实现 软性演员-评论家算法 SAC 优势原理 DDPG 的问题在于,训练不稳定、收敛差、依赖超参数、不适应复杂环境。 软性演员-评论家算法 SAC,更稳定…...

Nginx多域名部署多站点
目录 1.修改配置文件nginx.conf 2. 修改hosts文件 1.修改配置文件nginx.conf 在配置文件的 server_name 处修改成自己需要的域名,然后保存退出 j 查看语法是否错误,然后重启nginx nginx -t # 查看语法是否正确 systemctl restart nginx # 重启nginx …...

Java的常规面试题
Java的面试题主要涉及Java基础知识、并发编程、集合原理、JVM原理、I/O与网络编程、设计模式、互联网常用框架等多个领域[6]。一些常见的面试问题包括: 1. 面向对象的特征:继承、封装和多态性。 2. 访问修饰符public、private、protected以及默认时的区别…...

大数据技术发展史
文章目录 Google论文HadoopHive大数据生态 Google论文 今天我们常说的大数据技术,其实起源于Google在2004年前后发表的三篇论文,也就是我们经常听到的“三驾马车”,分别是分布式文件系统GFS、大数据分布式计算框架MapReduce和NoSQL数据库系统…...

linux常见基础指令
入门常见基础指令 ls、stat、 pwd 、cd、tree、 whoami、 touch、 mkdir、 rm 、 man、 cp、mv、cat、tac、echo、>、 >>、 < 、more、 less、 head、 tail、date、 cal、 find、 which、alias、whereis、grep、zip与unzip、 tar、bc、uname、xargs... 热键Tab、…...

“人家赚那么多”系列01:如何练习?练什么?
01 如何练习?练习什么? 今年计划重点围绕「在不骗自己的前提下,如何才能把事儿彻底做好,并做得有声有色?」为主题来写点儿东西,聊聊我是怎么做的,如何通过一些有效的方法来不断优化自己的。 想把…...

【Android】使用android studio查看内置数据库信息
要使用Android Studio查看内置数据库信息,可以按照以下步骤进行操作: 打开Android Studio并打开你的项目。 在左侧的Project窗口中,找到并展开你的app模块。 找到并展开"app" > "src" > "main"文件夹。…...

PHP开发日志 ━━ 基于PHP和JS的AES相互加密解密方法详解(CryptoJS) 适合CryptoJS4.0和PHP8.0
最近客户在做安全等保,需要后台登录密码采用加密方式,原来用个base64变形一下就算了,现在不行,一定要加密加key加盐~~ 前端使用Cypto-JS加密,传输给后端使用PHP解密,当然,前端虽然有key有盐&…...

2021-01-03 excel实现列递增,行保持不变
需求:excel文档数据操作的时候发现自动递增只能实现列不变行号递增 我这里里需要的是列递增行不变 解决方式:通过一些函数的组合使用 INDIRECT("驻场明细!"&CHAR(ROW()62)&ROW(驻场明细!A$28)) INDIRECT()函数的使用: INDI…...

[Python]两个杯子取水问题
利用两个杯子巧取三升水: 今天的这个趣味数学小游戏是利用两个没有刻度的水杯,巧妙地取出三升水来。 题目的条件是:一个总容量为6升的杯子和一个总容量为5升的杯子,同时面前有无限容量的水供你使用。不借助其它任何的容器…...

C++汇编语言学习计划
前几天买了某游戏的外挂,感觉外挂在我计算机上进行了不少操作,我想一探究竟,可是只有exe,没办法,翻译成汇编我也看不懂,索性来简单学习下。访问Chatgpt4,给了如下学习计划。 要从零开始学习C生成…...
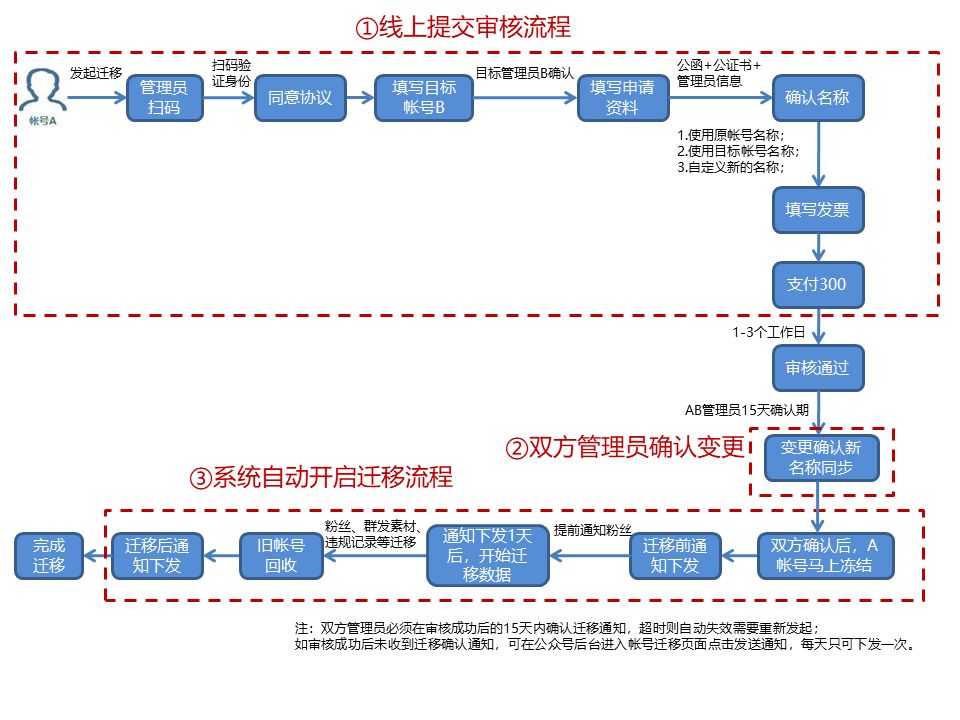
微信服务号升级订阅号条件
服务号和订阅号有什么区别?服务号转为订阅号有哪些作用?首先我们要看一下服务号和订阅号的主要区别。1、服务号推送的消息没有折叠,消息出现在聊天列表中,会像收到消息一样有提醒。而订阅号推送的消息是折叠的,“订阅号…...
SpringBoot整合mybatis多数据源
废话不多说先上结果 对应数据库 首先导入所需的mybatis、mysql和lombok依赖 <dependency><groupId>org.mybatis.spring.boot</groupId><artifactId>mybatis-spring-boot-starter</artifactId><version>2.2.2</version></dependen…...
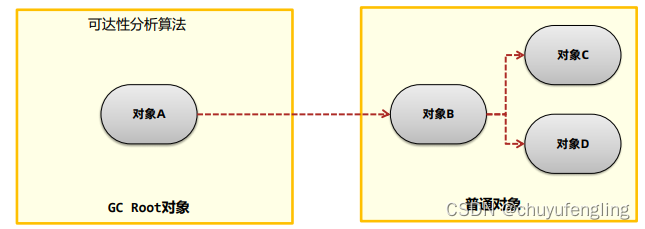
垃圾收集器与内存分配策略
内存分配和回收原则 对象优先在Eden区分配 大对象直接进入老年代 长期存活的对象进入老年代 什么是内存泄漏 不再使用的对象在系统中未被回收,内存泄漏的积累可能会导致内存溢出 自动垃圾回收与手动垃圾回收 自动垃圾回收:由虚拟机来自动回收对象…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...
