当前位置： 首页 > news >正文

隐藏层节点数对分类准确率的影响

news 2025/12/8 16:25:10

直线上有9个格子，4个石子，

数量

结构编号

6

0

1

1

1

1

0

0

0

0

0

5

2

1

1

1

0

1

0

0

0

0

5

1

1

0

1

1

1

0

0

0

0

4

3

1

1

0

0

1

1

0

0

0

4

4

1

0

1

0

1

1

0

0

0

3

5

1

0

1

0

1

0

1

0

0

有6个不同的结构

1

0

1

0

1

0

1

0

0

0

1

0

1

0

1

0

1

0

0

0

1

0

1

0

1

0

1

如结构5可能的置换有3个。这6个结构置换的数量顺序为0>2=1>3=4>5.

(A，B)---1*n*2---(1,0)(0,1)

做一个网络分类A和B，让A就是这6个结构，B全是0.用训练集做测试集

A

B

1-0

0-1

1

0

0.444

1

0.722

0*1

1

0

0.5

这个网络可能的合理分类方法只有两种，一种是认为1属于A，0属于B，则A的分类准确率是0.444，B的分类准确率是1，因为两个测试集图片数量相同，所以总的分类准确率是0.722.第二种方法是认为0和1都属于A，则A的准确率是1，B为0，平均是0.5.

现在让这个网络的隐藏层节点数为

20

16

15

12

10

8

6

4

2

210

190

170

150

130

110

90

70

50

30

410

390

370

350

330

310

290

270

250

230

610

590

570

550

530

510

490

470

450

430

810

790

770

750

730

710

690

670

650

630

2到810的共49个值，收敛误差为7e-4，每个n的每个结构收敛199次，取平均值。比较迭代次数和分类准确率的变化。

得到的6个结构的顺序为

810

5

4

1

0

3

2

310

0

1

2

3

4

5

790

5

4

2

3

0

1

290

0

1

2

3

4

5

770

4

5

3

1

0

2

270

0

1

2

3

4

5

750

5

4

0

3

1

2

250

0

1

2

3

4

5

730

5

4

0

3

2

1

230

0

1

2

3

4

5

710

5

4

3

0

2

1

210

0

1

2

3

4

5

690

5

4

3

0

2

1

190

0

1

2

3

4

5

670

5

3

4

0

2

1

170

0

2

1

3

4

5

650

4

5

0

3

2

1

150

0

2

1

3

4

5

630

4

3

0

5

2

1

130

0

2

1

3

4

5

610

0

5

3

4

2

1

110

0

1

2

3

4

5

590

3

0

1

4

2

5

90

0

2

1

3

4

5

570

3

0

1

2

4

5

70

0

2

1

3

4

5

550

3

0

1

2

4

5

50

0

2

1

3

4

5

530

1

3

0

2

4

5

30

0

2

1

3

4

5

510

1

3

0

2

4

5

20

0

2

1

3

4

5

490

1

3

0

2

4

5

16

0

2

1

3

4

5

470

1

3

0

2

4

5

15

0

2

1

3

4

5

450

3

0

1

2

4

5

12

0

2

1

3

5

4

430

0

3

1

2

4

5

10

0

2

3

1

4

5

410

0

1

3

2

4

5

8

2

0

1

3

5

4

390

0

1

3

2

4

5

6

0

2

3

4

1

5

370

0

1

3

2

4

5

4

5

0

1

2

3

4

350

0

1

2

3

4

5

2

0

2

1

3

4

5

330

0

1

2

3

4

5

只有16-90的第Ⅱ区顺序是稳定的，并且和计算顺序一致。n<16或n>90的顺序都变得混乱。

比较迭代次数的数据

比值

乘积

810

747.4422

753

764.6482

767.8543

773.0905

781.4121

1.05

632943.8

790

755.0704

759.9146

775.8945

784.4372

785.2211

786.1558

1.04

621063.1

770

765.1106

767.0503

787.4824

789.6935

795.5327

798.5176

1.04

614858.5

750

771.794

774.3869

793.7236

803.794

805.3819

805.8945

1.04

604420.9

730

776.4673

784.9698

804.8492

808.1156

815.2513

819.0101

1.05

597877.3

710

786.6683

795.3518

805.4523

812.3568

822.8794

826.2663

1.05

586649.1

690

801.7035

806.7588

812.3568

821.3116

831.0302

846.0754

1.06

583792

670

818.5377

819.9347

820.7286

834.0653

837.9146

859.0402

1.05

575556.9

650

826.8894

833.7538

847.995

849.7136

859.5528

908.0151

1.1

590209.8

630

832.2764

859.1407

860.1156

862.4271

914.2462

945.794

1.14

595850.2

610

872.6884

879.7839

892.9497

904.2965

930.3467

960.9899

1.1

586203.9

590

926.3266

926.6884

952.8693

958.4372

982.7889

1156.698

1.25

682452.1

570

976.3467

979.0603

991.8543

1012.638

1069.603

1244.196

1.27

709191.7

550

1039.211

1047.171

1050.266

1053.452

1175.161

1336.819

1.29

735250.5

530

1100.377

1107.774

1129.935

1140.015

1286.236

1466.618

1.33

777307.6

510

1174.186

1191.261

1219.844

1245.482

1438.377

1666.879

1.42

850108.5

490

1274.859

1292.116

1323.503

1374.92

1640.085

1977.854

1.55

969148.6

470

1404.749

1409.704

1437.834

1525.704

1896.789

2436.899

1.73

1145343

450

1561.211

1567.362

1569.191

1716.648

2226.307

3075.854

1.97

1384134

430

1718.779

1754.688

1765.563

1948.025

2664.005

3967.08

2.31

1705845

410

1902.487

2008.518

2009.221

2239.734

3261.804

5170.276

2.72

2119813

390

2130.698

2314.065

2372.749

2602.085

4089.613

6795.342

3.19

2650183

370

2442.759

2705.543

2892.035

3059.955

4988.085

8947.834

3.66

3310699

350

2902.437

3206.196

3617.05

3634.286

6105.302

11611.92

4

4064174

330

3580.467

3834.568

4301.141

4670.055

7456.749

14825.29

4.14

4892346

310

4480.106

4639.683

5159.261

6043.482

9064.266

18442.67

4.12

5717227

290

5409.503

5606.799

6218.095

7723.181

10894.39

22193.55

4.1

6436130

270

6202.95

6754.095

7529.472

9602.146

12904.78

25645.17

4.13

6924196

250

6879.261

8087.814

9140.698

11564.15

15053.65

28624.63

4.16

7156157

230

7539.472

9633.01

11109.66

13480.83

17323.91

30956.28

4.11

7119944

210

8259.925

11394.75

12548.27

15324.88

19684.45

32700.39

3.96

6867081

190

9140.116

13358.02

13594.44

16876.72

22087.49

33990.51

3.72

6458196

170

10199.22

14788.86

15172.74

18641.08

23904.1

34084.14

3.34

5794303

150

11521.18

16116.43

16294.62

20568.49

24188.75

32346.82

2.81

4852023

130

13172.66

17641.18

17681.79

22395.26

24748.56

31508.51

2.39

4096106

110

15335.37

19483.33

19552.62

24494.39

25861.12

31575.62

2.06

3473319

90

18231.47

21967.69

22060.23

26975.49

27672.07

32541.56

1.78

2928741

70

22283.1

25434.01

25893.23

30198.58

30638.54

34406.15

1.54

2408430

50

28214.42

30471.65

31501.27

34627.12

35155.54

37923.02

1.34

1896151

30

38335.66

39628.41

40700.18

42628.53

43286.57

44890.92

1.17

1346728

20

47392.38

48605.16

49894.38

50763.62

51584.3

52764.43

1.11

1055289

16

53654.12

55215.5

55892.45

56862.55

57756.04

58652.06

1.09

938432.9

15

56311.78

56624.75

57703.21

58880.99

59387.43

60366.67

1.07

905500

12

64075.93

64656.91

65501.91

66791.22

67267.99

67753.18

1.06

813038.2

10

71077.3

71915.43

73532.09

73680.97

74362.53

75526.56

1.06

755265.6

8

84117.8

84531.26

85455.77

85712.93

86315.25

86410.77

1.03

691286.2

6

103357.2

104393.6

105619.4

105846.8

105909.8

106796.6

1.03

640779.8

4

148083.9

148184.7

148217.1

148629.3

150324.7

150991

1.02

603963.9

2

259206.7

259809.3

260652.9

261047.7

261532.5

262058.4

1.01

524116.8

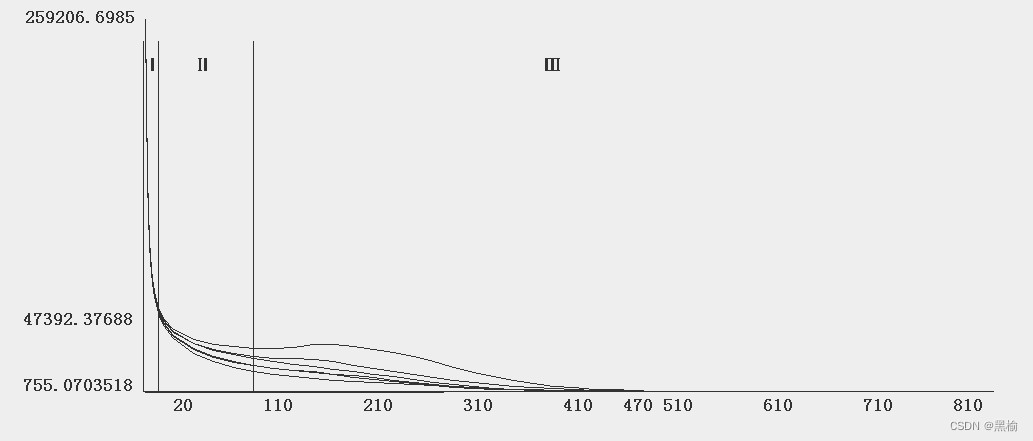
把中间段的曲线放大

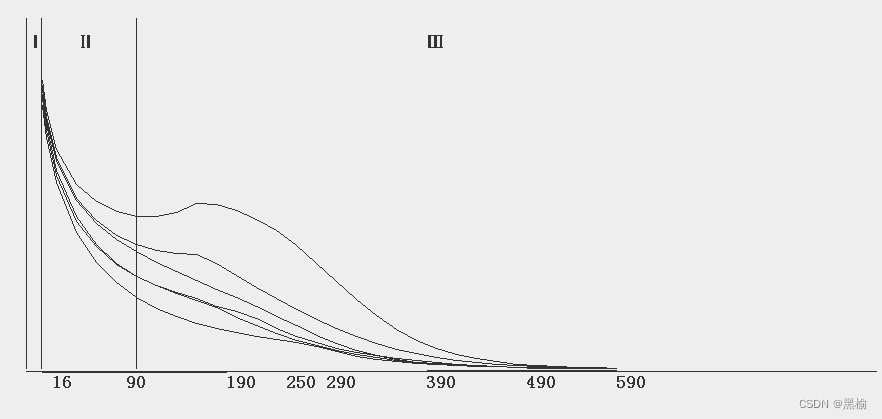
16-90区域几乎就是这条曲线分布最为规则的区域，分布稀疏间距均匀。

特别比较每组隐藏层节点数和迭代次数乘积的曲线

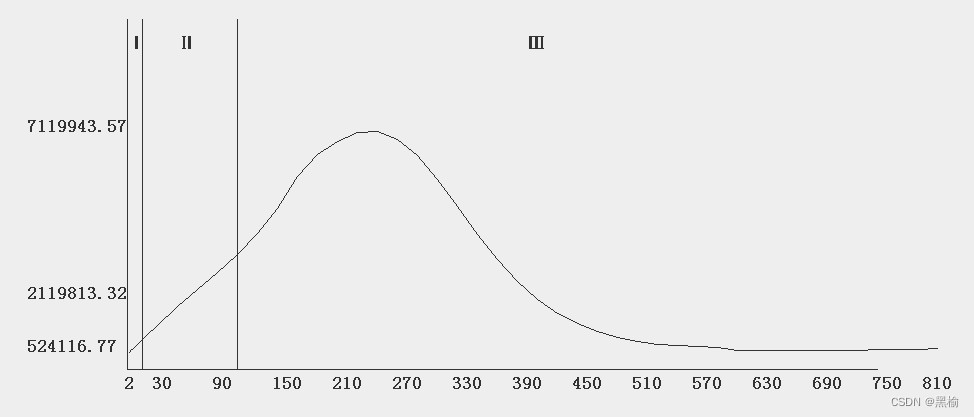
比如当n为2或810时

810

781.4121

632943.8

2

262058.4

524116.8

随着n的增加迭代次数d减小，但是n*d从没有小于524116的，当n=690的时候d已经和n相当，但是d的减小量小于n的增加量。所以在收敛误差一定的情况下n*d有极小值。就是2d=524116。所以用这个办法估算当n=100时的最大迭代次数应不小于5241，真实数值为这个数的6.6倍。

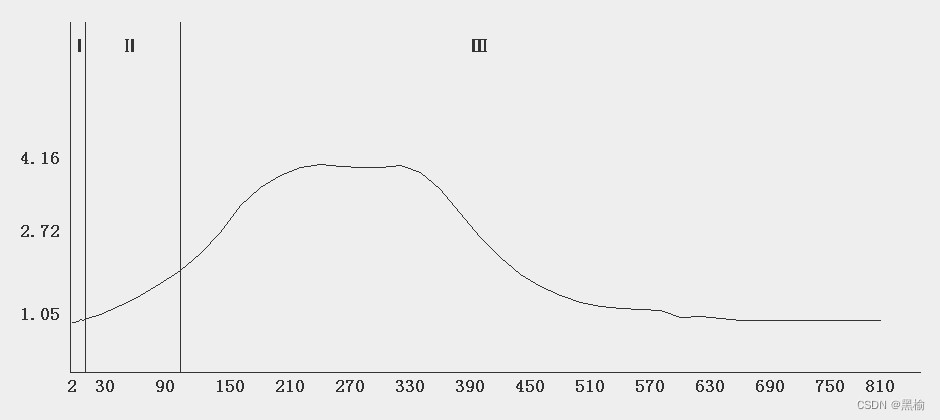
再比较同组迭代次数最大值和最小值的比例，在16-90区域这个值为1.09-1.78.这个值最大值为4.16.这条曲线和n*d的曲线很接近，结构上左右对称。

比较分类准确率

810

0.5

0.5

0.5

0.5

0.5

0.5

790

0.5

0.5

0.5

0.5

0.5

0.5

770

0.5

0.5

0.5

0.5

0.5

0.5

750

0.5

0.5

0.5

0.5

0.5

0.5

730

0.5

0.5

0.5

0.5

0.5

0.5

710

0.5

0.5

0.5

0.5

0.5

0.5

690

0.5

0.5

0.5

0.5

0.5

0.5

670

0.5

0.5

0.5

0.5

0.5

0.5

650

0.5

0.5

0.5

0.5

0.5

0.5

630

0.5

0.5

0.5

0.5

0.5

0.5

610

0.5

0.5

0.5

0.5

0.5

0.5

590

0.5

0.5

0.5

0.5

0.5

0.5

570

0.5

0.5

0.5

0.5

0.5

0.5

550

0.5

0.5

0.5

0.5

0.5

0.5

530

0.5

0.5

0.5

0.5

0.5

0.5

510

0.5

0.5

0.5

0.5

0.5

0.5

490

0.5

0.5

0.5

0.5

0.5

0.5

470

0.5

0.5

0.5

0.5

0.5

0.5

450

0.5

0.5

0.5

0.5

0.5

0.5

430

0.5

0.5

0.5

0.5

0.5

0.5

410

0.5

0.5

0.5

0.5

0.5

0.5

390

0.5

0.5

0.5

0.5

0.5

0.5

370

0.5

0.5

0.5

0.5

0.5

0.5

350

0.5

0.5

0.5

0.5

0.5

0.5

330

0.5

0.5

0.5

0.5

0.5

0.5

310

0.5

0.5

0.5

0.5

0.5

0.5

290

0.5

0.5

0.5

0.5

0.5

0.5

270

0.5

0.5

0.5

0.5

0.5

0.5

250

0.5

0.5

0.5

0.5

0.5

0.5

230

0.722222

0.5

0.5

0.5

0.5

0.5

210

0.722222

0.5

0.722222

0.5

0.5

0.5

190

0.5

0.5

0.5

0.5

0.5

0.5

170

0.5

0.5

0.5

0.5

0.5

0.5

150

0.5

0.5

0.5

0.5

0.722222

0.722222

130

0.5

0.722222

0.722222

0.722222

0.722222

0.722222

110

0.722222

0.722222

0.722222

0.722222

0.722222

0.722222

90

0.722222

0.722222

0.722222

0.722222

0.722222

0.722222

70

0.722222

0.722222

0.722222

0.722222

0.722222

0.722222

50

0.722222

0.722222

0.722222

0.722222

0.722222

0.722222

30

0.722222

0.722222

0.722222

0.722222

0.722222

0.722222

20

0.722222

0.722222

0.722222

0.722222

0.722222

0.722222

16

0.722222

0.722222

0.722222

0.722222

0.722222

0.722222

15

0.722222

0.722222

0.722222

0.722222

0.722222

0.722222

12

0.722222

0.722222

0.722222

0.722222

0.722222

0.722222

10

0.722222

0.722222

0.722222

0.722222

0.722222

0.722222

8

0.722222

0.722222

0.722222

0.722222

0.722222

0.722222

6

0.722222

0.722222

0.722222

0.722222

0.722222

0.722222

4

0.722222

0.722222

0.722222

0.722222

0.722222

0.722222

2

0.722222

0.722222

0.722222

0.722222

0.722222

0.722222

很意外的是Ⅰ区的分类准确率和Ⅱ区是相同的，而Ⅲ区用的第二种分类方法，分类性能从n=130开始变化。

Ⅰ区n<16，尽管迭代次数顺序混乱，但这并不影响分类性能

Ⅱ区16-90，迭代次数顺序和计算顺序一致，分类与计算结果也相同

Ⅲ区n>90，迭代次数顺序开始混乱，网络分类性能开始退化

相关文章：

隐藏层节点数对分类准确率的影响

直线上有9个格子&#xff0c;4个石子&#xff0c; 数量 结构编号 6 0 1 1 1 1 0 0 0 0 0 5 2 1 1 1 0 1 0 0 0 0 5 1 1 0 1 1 1 0 0 0 0 4 3 1 1 0 0 1 1 0 0 0 4 4 1 0 1 0 1 1 0 0 0 3 5 1 0 1 0 1 0 1 0…...

编程日记 2024/1/5 0:41:46

【水浸传感器】软硬件一体水浸监测整套方案远程监测解决各种环境漏水问题

一、痛点分析 在工业生产中&#xff0c;水浸传感器可以安装在数据中心、半导体厂房、输油管道、车间仓库、变电室等易发生水浸的区域。一旦检测到漏水情况&#xff0c;立即发出信号反馈。然而&#xff0c;水浸传感器分散在各个地点&#xff0c;导致管理不集中、不便捷&#xf…...

编程日记 2024/1/5 0:40:45

知虾会员**成为知虾会员，尊享专属权益**

在当今繁忙的生活中&#xff0c;线上购物已经成为现代人们的主要消费方式之一。而作为线上购物平台的领军者之一&#xff0c;Shopee为了提供更加个性化和便利的购物体验&#xff0c;推出了知虾会员&#xff08;Shopee会员&#xff09;服务。知虾会员不仅可以享受到一系列会员专…...

编程日记 2024/1/5 0:37:43

好代码网同款wordpress主题，适合搭建资源分享类网站，自带五六百的精品资源数据

代码简介&#xff1a; 好代码资源网是个还不错的资源分享类网站&#xff0c;基于wordpress搭建的。它的主题看起来还是不错的。这里分享一下这个网站的主题包。说是主题包&#xff0c;其实就是整站打包的&#xff0c;集成了主题&#xff08;wordpress美化主题包几个插件&#…...

编程日记 2024/1/5 0:36:42

Java多线程＜三＞常见的多线程设计模式

多线程的设计模式 两阶段线程终止 park方法 interrupted() 会让他失效。 使用volatile关键字进行改写 单例模式 双锁检测 保护性暂停 实现1&#xff1a; package threadBase.model;/*** author: Zekun Fu* date: 2022/5/29 19:01* Description:* 保护性暂停&#xff0c;* …...

编程日记 2024/1/5 0:35:41

JavaScript 基础二part1.运算符：赋值、一元、比较、逻辑运算符

JavaScript 基础二 1.1 赋值运算符1.2 一元运算符自增运算符的用法&#xff1a;例题 1.3 比较运算符不同类型间的比较严格相等对 null 和 undefined 进行比较 1.4 逻辑运算符例题 1.5 运算符优先级 1.1 赋值运算符 赋值运算符&#xff1a;对变量进行赋值的运算符 已经学过的赋…...

编程日记 2024/1/5 0:31:38

Linux 进程(八) 进程的退出码

main 函数的返回值叫做进程的退出码。当进程成功退出的时候&#xff0c;我们一般用0来表示。进程失败的时候一般用非零来表示。我们使用不同的数字来表示进程退出时不同的失败原因。 我们查看系统的有多少退出码以及其含义时需要用到strerror() 他的头文件和用法如下。 通过一…...

编程日记 2024/1/5 0:30:37

Go语言中支持的internal目录配置与组织内私网包配置详解

Go 中的内部包 这里可能会有歧义 可能是 Go 的 internal 目录中的包也可能是指内部开发的包 函数和变量的可见性 对于函数和变量而言&#xff0c;有如下规则&#xff1a;1 &#xff09;小写字母开头的函数变量结构体只能在本包内访问2 &#xff09;大写字母开头的函数变量结…...

编程日记 2024/1/5 0:29:36

如何使用Nmap加强网络安全？

Nmap是Network Mapper&#xff08;网络映射器&#xff09;的缩写&#xff0c;是一个用于端口和IP扫描以及应用程序检测的开源工具。网络和系统管理员将其用于清点网络资产、管理服务升级计划和监视服务正常运行时间。 起初&#xff0c;它是作为一款Linux工具而开发的&#xff…...

编程日记 2024/1/5 0:28:35

LeetCode 2487. 从链表中移除节点：单调栈

【LetMeFly】2487.从链表中移除节点&#xff1a;单调栈 力扣题目链接&#xff1a;https://leetcode.cn/problems/remove-nodes-from-linked-list/ 给你一个链表的头节点 head 。 移除每个右侧有一个更大数值的节点。 返回修改后链表的头节点 head 。 示例 1&#xff1a; 输…...

编程日记 2024/1/5 0:26:33

LabVIEW在高精度机器人视觉定位系统中的应用

在现代工业自动化中&#xff0c;精确的机器人视觉定位系统对于提高生产效率和产品质量至关重要。LabVIEW软件&#xff0c;以其卓越的图像处理和自动化控制功能&#xff0c;在这一领域发挥着重要作用。本案例将展示LabVIEW如何帮助开发和实现一个高精度的机器人视觉定位系统&…...

编程日记 2024/1/5 0:23:30

Arm CCA机密计算扩展

目录 Realms Realm World和Root World Arm TrustZone扩展和Arm RME之间有什么区别？ 在《什么是机密计算？》中所述，Arm CCA允许您在阻止更高特权软件实体（例如Hypervisor）访问的同时部署应用程序或虚拟机（VM）。然而，通常由这些特权软件实体管理内存等资源。在这种情况…...

编程日记 2024/1/5 0:22:30

【Unity入门】热更新框架之xLua

目录 一、xLua概述1.1xLua简介1.2xLua安装 二、Lua文件加载2.1执行字符串2.2加载Lua文件2.3自定义loader 三、xLua文件配置3.1打标签3.2静态列表3.3动态列表 四、Lua与C#交互4.1 C#访问Lua4.1.1 获取一个全局基本数据类型4.1.2 访问一个全局的table4.1.3 访问一个全局的functio…...

编程日记 2024/1/5 0:21:29

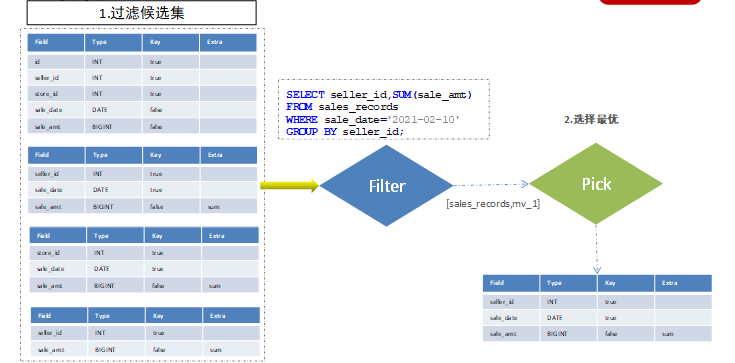
大数据Doris（四十五）：物化视图选择最优

文章目录 物化视图选择最优 物化视图选择最优 下面详细解释一下第一步最优物化视图是被如何选择出来的。 这里分为两个步骤： 对候选集合进行一个过滤。只要是查询的结果能从物化视图数据计算（取部分行，部分列，或部分行列的聚合）出都可以留在候选集中，过滤完成后候选集合…...

编程日记 2024/1/5 0:18:25

PostgreSQL10数据库源码安装及plpython2u、uuid-ossp插件安装

PostgreSQL10数据库源码安装及plpython2u、uuid-ossp插件安装 1、环境2、安装包下载3、安装3.1 、解压3.2、配置3.3、编译安装3.4 、启动与关闭 4、安装 uuid-ossp 、plpython2u插件5、参考 1、环境 centos 7 、 postgresql 10.19 2、安装包下载 postgres 源码安装包 3、安…...

编程日记 2024/1/5 0:09:15

如何成为ChatGPT 优质Prompt创作者

如何提问&#xff1f; 我想让你成为我的Prompt创作者。你的目标是帮助我创作最佳的Prompt&#xff0c;这个Prompt将由你ChatGPT使用。你将遵循 以下过程&#xff1a;1.首先&#xff0c;你会问我Prompt是关于什么&#xff1f;我会告诉你&#xff0c;但我们需要 通过不断的重复来…...

编程日记 2024/1/5 0:08:15

LeetCode第71题 - 简化路径

题目 以 Unix 风格给出一个文件的绝对路径&#xff0c;你需要简化它。或者换句话说&#xff0c;将其转换为规范路径。 在 Unix 风格的文件系统中&#xff0c;一个点&#xff08;.&#xff09;表示当前目录本身&#xff1b;此外&#xff0c;两个点 &#xff08;…&#xff09; 表…...

编程日记 2024/1/5 0:07:14

VSCode上远程调试代码出现的问题

记录一下&#xff1a; 真的是汗流浃背了&#xff0c;师妹叫帮忙如何在VSCode上远程调试代码&#xff0c;一些自己已经经历过的问题&#xff0c;现在已经忘记了。又在网上一顿搜索&#xff0c;这次记录下吧。。。 出现以下问题&#xff1a; 1. 终端界面总是sh-4.4 $ &#xff…...

编程日记 2024/1/5 0:06:13

【langchain】入门初探实战笔记（Chain, Retrieve, Memory, Agent）

1. 简介 1.1 大语言模型技术栈 大语言模型技术栈由四个主要部分组成&#xff1a; 数据预处理流程&#xff08;data preprocessing pipeline&#xff09;嵌入端点&#xff08;embeddings endpoint &#xff09;向量存储&#xff08;vector store&#xff09;LLM 终端&#xff…...

编程日记 2024/1/5 0:03:10

《数据结构、算法与应用C++语言描述》- 平衡搜索树 -全网唯一完整详细实现插入和删除操作的模板类

平衡搜索树 完整可编译运行代码见&#xff1a;Github::Data-Structures-Algorithms-and-Applications/_34Balanced search tree 概述 本章会讲AVL、红-黑树、分裂树、B-树。 平衡搜索树的应用&#xff1f; AVL 和红-黑树和分裂树适合内部存储的应用。 B-树适合外部存储的…...

编程日记 2024/1/5 0:02:09

JavaSec-RCE

简介 RCE(Remote Code Execution)&#xff0c;可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景&#xff1a;Groovy代码注入 Groovy是一种基于JVM的动态语言&#xff0c;语法简洁&#xff0c;支持闭包、动态类型和Java互操作性&#xff0c…...

编程新知 2025/12/7 7:55:23

el-switch文字内置

el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

编程新知 2025/11/27 12:34:31

MySQL 8.0 OCP 英文题库解析（十三）

Oracle 为庆祝 MySQL 30 周年&#xff0c;截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始&#xff0c;将英文题库免费公布出来&#xff0c;并进行解析&#xff0c;帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

编程新知 2025/12/6 21:00:55

C++八股 —— 单例模式

文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全&#xff08;Thread Safety&#xff09; 线程安全是指在多线程环境下&#xff0c;某个函数、类或代码片段能够被多个线程同时调用时&#xff0c;仍能保证数据的一致性和逻辑的正确性&#xf…...

编程新知 2025/12/2 3:35:50

【C++进阶篇】智能指针

C内存管理终极指南&#xff1a;智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

编程新知 2025/11/30 3:13:04

MySQL 索引底层结构揭秘：B-Tree 与 B+Tree 的区别与应用

文章目录 一、背景知识&#xff1a;什么是 B-Tree 和 BTree&#xff1f; B-Tree&#xff08;平衡多路查找树&#xff09; BTree&#xff08;B-Tree 的变种&#xff09; 二、结构对比&#xff1a;一张图看懂 三、为什么 MySQL InnoDB 选择 BTree&#xff1f; 1. 范围查询更快 2…...

编程新知 2025/12/3 6:15:50

如何应对敏捷转型中的团队阻力

应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中&#xff0c;明确沟通敏捷转型目的尤为关键&#xff0c;团队成员只有清晰理解转型背后的原因和利益&#xff0c;才能降低对变化的…...

编程新知 2025/12/5 0:32:22

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG

TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码&#xff1a;HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...

编程新知 2025/12/7 20:24:29

WebRTC调研

WebRTC是什么&#xff0c;为什么&#xff0c;如何使用 WebRTC有什么优势 WebRTC Architecture Amazon KVS WebRTC 其它厂商WebRTC 海康门禁WebRTC 海康门禁其他界面整理 威视通WebRTC 局域网 Google浏览器 Microsoft Edge 公网 RTSP RTMP NVR ONVIF SIP SRT WebRTC协…...

编程新知 2025/12/5 21:11:55

Xcode 16 集成 cocoapods 报错

基于 Xcode 16 新建工程项目&#xff0c;集成 cocoapods 执行 pod init 报错 ### Error RuntimeError - PBXGroup attempted to initialize an object with unknown ISA PBXFileSystemSynchronizedRootGroup from attributes: {"isa">"PBXFileSystemSynchro…...

编程新知 2025/11/29 6:41:01