《数据结构、算法与应用C++语言描述》- 平衡搜索树 -全网唯一完整详细实现插入和删除操作的模板类
平衡搜索树
完整可编译运行代码见:Github::Data-Structures-Algorithms-and-Applications/_34Balanced search tree
概述
本章会讲AVL、红-黑树、分裂树、B-树。
平衡搜索树的应用?
AVL 和红-黑树和分裂树适合内部存储的应用。
B-树适合外部存储的应用,例如,存储在磁盘上的大型词典。
STL类map 和 multimap使用的是红-黑树结构,以保证查找、插入和删除操作具有对数级的时间性能。
什么时候适合用平衡搜索树?
- 按关键字实施字典操作,而且操作时间不能超过指定的范围。
- 按名次实施的查找和删除操作。
- 不按精确的关键字匹配所进行的字典操作(例如寻找关键字大于k的最小元素)。
AVL和红-黑树的旋转?
AVL树对每个插人操作最多需要一次旋转,对每个删除操作最多需要O(logn)次旋转。
红-黑树对每个插入和删除操作,都只需要一次旋转。
当一次旋转只需用时 Θ ( 1 ) \Theta(1) Θ(1)时,他们之间的区别不明显。但是当一次旋转的时间复杂度比较高时,比如平衡优先搜索树。平衡优先搜索树用于描述具有二维关键字的元素,此时,每个关键字是一数对(x,y)。它是关于y的优先队列,同时又是关于x的搜索树。在这样的树中,每一次旋转都需耗时 O(logn)。如果用红-黑树来描述平衡优先搜索树,则因为每一次插入或删除仅需要执行一次旋转,所以插入或删除操作的总时间仍保持为O(logn)。当使用AVL树时,则删除操作的时间将变为 O ( l o g 2 n ) O(log^2n) O(log2n)。
AVL树
定义
如果搜索树的高度总是O(logn),我们就能保证查找、插人和删除的时间为O(logn)。最坏情况下的高度为O(logn)的树称为平衡树(balanced tree)。比较流行的一种平衡树是AVL树(AVL tree),它是Adelson-Velskii 和 Landis在 1962年提出的。
定义15-1一棵空的二叉树是AVL树;如果T是一棵非空的二叉树, T L T_L TL和 T R T_R TR分别是其左子树和右子树,那么当T满足以下条件时,T是一棵AVL树:
1) T L T_L TL和 T R T_R TR是AVL树;2) ∣ h L − h R ∣ < 1 |h_L-h_R|<1 ∣hL−hR∣<1,其中 h L h_L hL和 h R h_R hR分别是 T L T_L TL和 T R T_R TR的高。
一棵AVL搜索树既是二叉搜索树,也是AVL树。
一棵索引AVL搜索树既是索引二叉搜索树,也是AVL树。
用AVL搜索树来描述字典的要求
如果用AVL搜索树来描述字典,并在对数级时间内完成每一种字典操作,那么,我们必须确定AVL树的下述特征:
1)一棵n个元素的AVL树,其高度是O(logn)。
2)对于每一个n, n ≥ 0 n\geq 0 n≥0,都存在一棵AVL树。
3)对一棵n元素的AVL搜索树,在O(高度)=O(logn)的时间内可以实现查找。
4)将一个新元素插入一棵n元素的AVL搜索树中,可以得到一棵n+1个元素的AVL树,而且插人用时为O(logn)。
5)一个元素从一棵n元素的AVL搜索树中删除,可以得到一棵n-1个元素的AVL树,而且删除用时为O(logn)。
AVL树的高度
对一棵高度为h的AVL树,令 N h N_h Nh是其最少的节点数。在最坏情况下,根的一棵子树的高度是h-1,另一棵子树的高度是h-2,而且两棵子树都是AVL树。因此有:
N h = N h − 1 + N h − 2 + 1 , N 0 = 0 且 N 1 = 1 N_h=N_{h-1}+N_{h-2}+1,N_0=0且N_1=1 Nh=Nh−1+Nh−2+1,N0=0且N1=1
N h N_h Nh的定义与斐波拉契数列的定义是相似的:
F n = F n − 1 + F n − 2 , F 0 = 0 且 F 1 = 1 F_n = F_{n - 1} + F_{n-2}, F_0=0且F_1 = 1 Fn=Fn−1+Fn−2,F0=0且F1=1
经分析可得 N h N_h Nh的列表为:1,2,4,7,12,20,33…
F n F_n Fn的列表为:1,1,2,3,5,8,13,21,34…
因此 N h N_h Nh可以表示为:
N h = F h + 2 − 1 , h ≥ 0 N_h=F_{h+2}-1,h\geq 0 Nh=Fh+2−1,h≥0
由斐波拉契定理可知:
F h = ϕ h 5 F_h=\frac{\phi^h}{\sqrt{5}} Fh=5ϕh,其中 ϕ = 1 + 5 2 \phi=\frac{1+\sqrt{5}}{2} ϕ=21+5,因此 N h ≈ ϕ h + 2 5 − 1 N_h\approx\frac{\phi^{h+2}}{\sqrt{5}}-1 Nh≈5ϕh+2−1。如果树中有n个节点,那么树的最大高度为: l o g ϕ ( 5 ( n + 1 ) ) − 2 ≈ 1.44 l o g 2 ( n + 2 ) = O ( l o g n ) log_{\phi}(\sqrt{5}(n+1))-2\approx1.44log_2(n+2)=O(logn) logϕ(5(n+1))−2≈1.44log2(n+2)=O(logn)。
证明了AVL树的最大高度满足O(logn)。
AVL树的描述
链表描述-平衡因子
AVL树一般用链表描述。但是,为简化插入和删除操作,我们为每个节点增加一个平衡因子bf。节点x的平衡因子bf(x)定义为:x的左子树高度-x的右子树高度
从AVL树的定义可以知道,平衡因子的可能取值为-1、0和1。图15-1是两棵带有平衡因子的AVL搜索树。

AVL树的搜索
与二叉搜索树的搜索方法一致。
假设要查找关键字为theKey的元素。先从根开始查找。如果根为空,那么搜索树不包含任何元素,即查找失败。如果不空,则将 theKey与根的关键字相比较。如果 theKey小,那么就不必在右子树中查找,只要查找左子树。如果theKey大,则正好相反,只需查找右子树。如果 theKey等于根的关键字,则查找成功。时间复杂度为O(n)。
AVL树的插入
插入新的元素可能会导致不平衡。在插入之前,从根节点往下移动寻找插入新元素的位置时,设X是最后一个具有-1或1平衡因子的节点。
如果节点X不存在,那么从根节点至新插入节点的途径中,所有节点在插入前的平衡因子都是0。由于插人操作只会使平衡因子增减0或1,并且只有从根节点至新插入节点的途径中的节点的平衡因子会被改变,所以插入后,树的平衡不会被破坏。因此,只有插人后的树是不平衡的,X才存在。
一棵树从平衡变为不平衡的唯一过程是:在插人操作之后,平衡因子bf(X)的值由-1变为-2,或者由1变为2。当插入元素后,X是离新插入节点最近的祖先,且平衡因子是-2或2。
节点X的不平衡情况有两类:L型不平衡(新插人节点在X的左子树中)和R型不平衡。
L型不平衡可以分为两类:
- LL:新插入节点在X节点的左子树的左子树中

- LR:新插入节点在X节点的左子树的右子树中

R型不平衡可以分为两类:
- RL:新插入节点在X节点的右子树的左子树中

- RR:新插入节点在X节点的右子树的右子树中

因此,AVL树中插入节点可能会导致不平衡的情况总共分为四类。
解决不平衡的方法:
LL旋转
下图是一种普通的LL型不平衡。图a是插入前的条件,图b是在节点B的左子树BL中插人一个元素后的情形。恢复平衡所进行的子树移动如图c所示。原来以X为根节点的子树,现在以B为根节点,BL’仍然是B的左子树,X变成B的右子树的根,BR变成X的左子树,X的右子树不变。随着X的平衡因子的改变,在从B到新插入节点的路径上,BL’的所有节点的平衡因子都要改变。其他节点的平衡因子与旋转前的一致。因为图a和图c的子树的高度是一样的,所以它们的祖父节点如果存在的话,其平衡因子与插入前是一样的。因此所有节点的平衡因子都是-1、0或1。

LR旋转
下图给出了一种普通的LR型不平衡。因为插人操作发生在B的右子树,所以这棵子树在插入后不可能为空,因此节点C是存在的。但是,C的子树CL和CR有可能为空。为了恢复平衡,需要对子树进行重新整理,如图c所示,将C作为根,B作为C的左子树,B的左子树不变,B的右子树指向C的左子树;X作为C的右子树,X的左子树指向C的右子树,X的右子树不变。重新整理后,bf(B)和 bf(X)的值取决于bf(C)在插入之后、重新整理之前的值b。重新整理后的子树仍是二叉搜索树。另外,因为图a 和图c的子树的高度是相同的,所以它们的祖先如果存在,其平衡因子在插入前与在插入后也是相同的。因此,在节点A的一个LR旋转即可完成整个树的重新平衡。
可以理解为X的左孩子的RR旋转和X的LL旋转。
注意事项:需要检查X的左孩子的右孩子是否存在,如果存在,则执行此算法;如果不存在,则需要执行LL算法。

RR旋转
下图是一种普通的RR型不平衡。图a是插入前的条件,图b是在节点B的右子树BR中插人一个元素后的情形。恢复平衡所进行的子树移动如图c所示。原来以X为根节点的子树,现在以B为根节点,BR’仍然是B的右子树,X变成B的左子树的根,BL变成X的右子树,X的左子树不变。随着X的平衡因子的改变,在从B到新插入节点的路径上,BR’的所有节点的平衡因子都要改变。其他节点的平衡因子与旋转前的一致。因为图a和图c的子树的高度是一样的,所以它们的祖父节点如果存在的话,其平衡因子与插入前是一样的。因此所有节点的平衡因子都是-1、0或1。

RL旋转
下图给出了一种普通的RL型不平衡。因为插人操作发生在B的左子树,所以这棵子树在插入后不可能为空,因此节点C是存在的。但是,C的子树CL和CR有可能为空。为了恢复平衡,需要对子树进行重新整理,如图c所示,将C作为根,B作为C的右子树,B的右子树不变,B的左子树指向C的右子树;X作为C的左子树,X的右子树指向C的左子树,X的左子树不变。重新整理后,bf(B)和 bf(X)的值取决于bf(C)在插入之后、重新整理之前的值b。重新整理后的子树仍是二叉搜索树。另外,因为图a 和图c的子树的高度是相同的,所以它们的祖先如果存在,其平衡因子在插入前与在插入后也是相同的。因此,在节点A的一个RL旋转即可完成整个树的重新平衡。
可以理解为X的右孩子的LL旋转和X的RR旋转。
注意事项:需要检查X的右孩子的左孩子是否存在,如果存在,则执行此算法;如果不存在,则需要执行LL算法。

插入节点的步骤
使用递归的方法:沿着从根节点开始的路径,根据新元素的关键字,去寻找新元素的插入位置。
- 终止条件:所传递的参数cur节点为nullptr。new一个新的AVLTreeNode节点。
- 如果插入元素的键值大于当前节点的键值,则递归到当前节点的左孩子。根据当前cur的bf值决定是否执行LL旋转或LR旋转。
- 如果插入元素的键值小于当前节点的键值,则递归到当前节点的右孩子。根据当前cur的bf值决定是否执行RR旋转或RL旋转。
- 如果插入元素的键值等于当前节点的键值,则更新当前节点的值为新的值。
- 每轮递归都要更新当前节点的高度。
AVL树的删除
删除一个节点后,记录其父亲节点q。如果要删除图15-1b中关键字为25的元素,那么该元素的节点被删除,并且根节点的右孩子指针指向被删除节点的唯一孩子。因为根节点是被删除节点的父节点,所以q就是根节点。如果要删除的是关键字为15的元素,那么该元素的节点将被关键字为12的元素所占用,而
12的原节点被删除。这时的q是原15的节点(根的左孩子)。
**从根到q的路径上的一些节点或全部节点的平衡因子都可能会改变,所以要从q沿原路折回,可以使用栈存储被删除节点的所有祖先,以便后续调整平衡树。**如果删除发生在q的左子树,那么bf(q)减1。如果删除发生在q的右子树,那么bf(q)加1。下面是删除的几种情形:
- D1:如果q的新平衡因子是0,那么它的高度减少了1,这时需要改变它的父节点(如果有的话)的平衡因子,而且可能需要改变其他祖先节点的平衡因子。
- D2:如果q的新平衡因子是-1或1,那么它的高度与删除前相同,而且无需改变其祖先的平衡因子值。
- D3:如果q的新平衡因子是-2或2,那么树在q处是不平衡的。
从q到根节点的路径上,节点的平衡因子可能发生很大变化,有的节点的平衡因子有可能变为-2或2。令A是第一个这样的节点。要恢复A节点的平衡,需要根据不平衡的类型而定。如果删除发生在A的左子树,那么不平衡类型是L型;否则,不平衡类型就是R型。如果在删除后,bf(A)=2,那么在删除前,bf(A)的值一定为1。因此,A有一棵以B为根的左子树。根据bf(B)的值,可以把一个R型不平衡细分为R0,R1和R-1,把一个L型不平衡细分为L0,L1和L-1。
- R0型:就是B节点的bf为0。子树的高度在删除前和删除后都是h+2,因此,到根节点途径上的剩余节点没有改变平衡因子,整棵树在一次旋转后获得平衡。其实和LL旋转一样的操作。

- R1型:B节点的bf为1。旋转后子树的高度是h+1,比删除前减少了1。因此,如果A不是根节点,它的某些祖先的平衡因子将产生变化,可能需要进行旋转以保持平衡。R1旋转后,必须继续检查至根节点路径上的节点。其实和LL旋转一样的操作。

- R-1型:B节点的bf为-1。节点A和B在旋转后的平衡因子取决于B的右孩子的平衡因子b。这次旋转得到了一棵高度为h1的子树,而删除前的子树高度是h+2,因此,在至根节点的路径上需要继续旋转。先来一次B节点的L0旋转,再来一次A节点的R0旋转。

L0,L1,L-1与R0,R1和R-1差不多,只是方向不同。
代码
AVLTree.h
/*
Project name : _34Balanced_search_tree
Last modified Date: 2023年12月27日10点57分
Last Version: V1.0
Descriptions: AVL树模板类
*/#ifndef _34BALANCED_SEARCH_TREE_AVLTREE_H
#define _34BALANCED_SEARCH_TREE_AVLTREE_H
#include "AVLTreeNode.h"
#include "dictionary.h"
#include <stack>
using namespace std;void AVLTreeTest();template<class K, class E>
class AVLTree : public dictionary<K,E>{
public:AVLTree(){root = nullptr;treeSize = 0;}[[nodiscard]] bool empty() const {return treeSize == 0;}[[nodiscard]] int size() const {return treeSize;}pair<K, E>* find(K theKey) const;void insert(pair<K, E>& thePair) {insert(thePair, root);}void erase(K theKey);/*中序遍历二叉树,使用函数指针的目的是是的本函数可以实现多种目的*/void inOrder(void(*theVisit)(AVLTreeNode<pair<K, E>>*)){visit = theVisit;/*是因为递归,所以才要这样的*/inOrder(root);/*这里调用的是静态成员函数inOrder()*/}/*中序遍历---输出endl*/void inOrderOutput() { inOrder(output); cout << endl; }/*前序遍历二叉树,使用函数指针的目的是是的本函数可以实现多种目的*/void preOrder(void(*theVisit)(AVLTreeNode<pair<K, E>>*)){visit = theVisit;/*是因为递归,所以才要这样的*/preOrder(root);/*这里调用的是静态成员函数preOrder()*/}/*中序遍历---输出endl*/void preOrderOutput() { preOrder(output); cout << endl; }private:AVLTreeNode<pair<K, E>>* root;// 指向根的指针int treeSize;// 树的结点个数static void (*visit)(AVLTreeNode<pair<K, E>>*);//是一个函数指针,返回值为void 函数参数为binaryTreeNode<pair<K, E>>*static void output(AVLTreeNode<pair<K, E>>* t) { cout << *t << endl; }static void inOrder(AVLTreeNode<pair<K, E>>* t);static void preOrder(AVLTreeNode<pair<K, E>>* t);void rotateLL(AVLTreeNode<pair<K, E>>*& x);void rotateLR(AVLTreeNode<pair<K, E>>*& x);void rotateRR(AVLTreeNode<pair<K, E>>*& x);void rotateRL(AVLTreeNode<pair<K, E>>*& x);void insert(pair<K, E>& thePair, AVLTreeNode<pair<K, E>>*& cur);
};/*私有静态成员初始化*/
/*这里是静态函数指针成员的初始化,不初始化会引发LINK错误*/
template<class K, class E>
void (*AVLTree<K,E>::visit)(AVLTreeNode<pair<K, E>>*) = 0; // visit function/*中序遍历 递归*/
template<class K, class E>
void AVLTree<K,E>::inOrder(AVLTreeNode<pair<K, E>>* t)
{if (t != nullptr){inOrder(t->leftChild);/*中序遍历左子树*/visit(t);/*访问树根*/inOrder(t->rightChild);/*中序遍历右子树*/}
}/*前序遍历 递归*/
template<class K, class E>
void AVLTree<K,E>::preOrder(AVLTreeNode<pair<K, E>>* t)
{if (t != nullptr){visit(t);/*访问树根*/preOrder(t->leftChild);/*中序遍历左子树*/preOrder(t->rightChild);/*中序遍历右子树*/}
}/* 查找元素* 输入:theKey表示需要查找元素的键值* 输出:键值为theKey的节点的pair地址* 时间复杂度:O(logn),n表示节点个数*/
template<class K, class E>
pair<K, E>* AVLTree<K,E>::find(K theKey) const
{// 返回值是匹配数对的指针// 如果没有匹配的数对,返回值为nullptr// p从根节点开始搜索,寻找关键字等于theKey的一个元素AVLTreeNode<pair<K, E> > *p = root;while (p != nullptr)// 检查元素 p->elementif (theKey < p->element.first)p = p->leftChild;elseif (theKey > p->element.first)p = p->rightChild;else // 找到匹配的元素return &p->element;// 没找到匹配的元素return nullptr;
}/** LL旋转:在x的左孩子的左孩子插入元素的时候使用* 输入:AVLTreeNode<pair<K, E>>* x,x表示从根节点往下移动寻找插入新元素的位置时,最后一个具有-1或1平衡因子的节点。* 输出:void* 时间复杂度:O(1)*/
template<class K, class E>
void AVLTree<K,E>::rotateLL(AVLTreeNode<pair<K, E>>*& x){AVLTreeNode<pair<K, E>>* b = x->leftChild;x->leftChild = b->rightChild;b->rightChild = x;// 更新x的高度if(x->leftChild != nullptr && x->rightChild != nullptr)x->height = max(x->leftChild->height, x->rightChild->height) + 1;else if(x->leftChild != nullptr)x->height = x->leftChild->height + 1;else if(x->rightChild != nullptr)x->height = x->rightChild->height + 1;elsex->height = 1;// 更新b的高度if(b->leftChild != nullptr && b->rightChild != nullptr)b->height = max(b->leftChild->height, b->rightChild->height) + 1;else if(b->leftChild != nullptr)b->height = b->leftChild->height + 1;else if(x->rightChild != nullptr)b->height = b->rightChild->height + 1;elseb->height = 1;x = b;
}
/** RR旋转:在x的右孩子的右孩子插入元素的时候使用* 输入:AVLTreeNode<pair<K, E>>* x,x表示从根节点往下移动寻找插入新元素的位置时,最后一个具有-1或1平衡因子的节点。* 输出:void* 时间复杂度:O(1)*/
template<class K, class E>
void AVLTree<K,E>::rotateRR(AVLTreeNode<pair<K, E>>*& x){AVLTreeNode<pair<K, E>>* b = x->rightChild;x->rightChild = b->leftChild;b->leftChild = x;// 更新x的高度if(x->leftChild != nullptr && x->rightChild != nullptr)x->height = max(x->leftChild->height, x->rightChild->height) + 1;else if(x->leftChild != nullptr)x->height = x->leftChild->height + 1;else if(x->rightChild != nullptr)x->height = x->rightChild->height + 1;elsex->height = 1;// 更新b的高度if(b->leftChild != nullptr && b->rightChild != nullptr)b->height = max(b->leftChild->height, b->rightChild->height) + 1;else if(b->leftChild != nullptr)b->height = b->leftChild->height + 1;else if(x->rightChild != nullptr)b->height = b->rightChild->height + 1;elseb->height = 1;x = b;
}
/** LR旋转:在x的左孩子的右孩子插入元素的时候使用* 输入:AVLTreeNode<pair<K, E>>* x,x表示从根节点往下移动寻找插入新元素的位置时,最后一个具有-1或1平衡因子的节点。* 输出:void* 时间复杂度:O(1)*/
template<class K, class E>
void AVLTree<K,E>::rotateLR(AVLTreeNode<pair<K, E>>*& x){rotateRR(x->leftChild);rotateLL(x);
}/** RL旋转:在x的右孩子的左孩子插入元素的时候使用* 输入:AVLTreeNode<pair<K, E>>* x,x表示从根节点往下移动寻找插入新元素的位置时,最后一个具有-1或1平衡因子的节点。* 输出:void* 时间复杂度:O(1)*/
template<class K, class E>
void AVLTree<K,E>::rotateRL(AVLTreeNode<pair<K, E>>*& x){rotateLL(x->rightChild);rotateRR(x);
}/** 插入元素* 输入:const pair<K, E> thePair表示需要插入的键值对* 输出:void* 时间复杂度:O(logn),表示节点个数*/
template<class K, class E>
void AVLTree<K,E>::insert(pair<K, E>& thePair, AVLTreeNode<pair<K, E>>*& cur)
{if(cur == nullptr){cur = new AVLTreeNode<pair<K, E> > (thePair, nullptr, nullptr);treeSize++;}else if(thePair.first < cur->element.first){insert(thePair, cur->leftChild);// 计算bf,检查bf是否 == 2,如果是需要调整平衡int bf = 0;if(cur->leftChild != nullptr && cur->rightChild != nullptr)bf = cur->leftChild->height - cur->rightChild->height;else if(cur->leftChild != nullptr)bf = cur->leftChild->height;else if(cur->rightChild != nullptr)bf = 0 - cur->rightChild->height;elsebf = 0;if(bf == 2){if(thePair.first < cur->leftChild->element.first)// 左左插入rotateLL(cur);// 单旋转else // 左右插入{if(cur->leftChild->rightChild == nullptr)rotateLL(cur);// 当当前节点的左孩子的右孩子为空时,找不到示意图中替换的C节点elserotateLR(cur);}}}else if(thePair.first > cur->element.first){insert(thePair, cur->rightChild);// 计算bf,检查bf是否等于-2,如果是需要调整平衡int bf = 0;if(cur->leftChild != nullptr && cur->rightChild != nullptr)bf = cur->leftChild->height - cur->rightChild->height;else if(cur->leftChild != nullptr)bf = cur->leftChild->height;else if(cur->rightChild != nullptr)bf = 0 - cur->rightChild->height;elsebf = 0;if(bf == -2){if(thePair.first > cur->rightChild->element.first) // 右右插入rotateRR(cur);// 单旋转else // 右左插入{if(cur->rightChild->leftChild == nullptr)rotateRR(cur);// 当当前节点的左孩子的右孩子为空时,找不到示意图中替换的C节点elserotateRL(cur);}}}else// 如果键值已经存在的话,就更新元素cur->element.second = thePair.second;// 更新cur节点的高度if(cur->leftChild != nullptr && cur->rightChild != nullptr)cur->height = max(cur->leftChild->height, cur->rightChild->height) + 1;else if(cur->leftChild != nullptr)cur->height = cur->leftChild->height + 1;else if(cur->rightChild !=nullptr)cur->height = cur->rightChild->height + 1;elsecur->height = 1;
}
/** 删除元素* 输入:const K theKey表示需要删除元素的键值* 输出:void* 时间复杂度:O(logn),n表示节点个数*/
template<class K, class E>
void AVLTree<K,E>::erase(K theKey)
{// 删除关键字等于theKey的数对// 查找关键字为theKey的节点// 前面的删除节点的步骤与二叉搜索树的一致;但是要记录一下路径stAVLTreeNode<pair<K, E> > *p = root,*pp = nullptr;stack<AVLTreeNode<pair<K, E> > *> st;// 记录轨迹while (p != nullptr && p->element.first != theKey){pp = p;st.push(pp);// 记录轨迹if (theKey < p->element.first)p = p->leftChild;elsep = p->rightChild;}if (p == nullptr)return; // 不存在与关键字theKey匹配的数对// 重新组织树结构// 当p有两个孩子时的处理if (p->leftChild != nullptr && p->rightChild != nullptr){// 两个孩子// 在P的左子树中寻找最大元素AVLTreeNode<pair<K, E> > *s = p->leftChild,*ps = p; // s的父节点while (s->rightChild != nullptr){// 移动到更大的pairps = s;st.push(ps);// 记录轨迹s = s->rightChild;// 右孩子比较大}// 将最大元素s移到p// p->element = s->element 的键值是 const// 当最大值就是p的左孩子时,new的元素不能直接指向p的左孩子,而要指向p的左孩子的左孩子(此时p的左孩子没有右孩子),因为到时候s会被delete掉,这个问题在后面的p至多有一个孩子那里解决的AVLTreeNode<pair<K, E> >* q = nullptr;q = new AVLTreeNode<pair<K, E> >(s->element, p->leftChild, p->rightChild, p->height);// pp是p的父节点// 如果p没有父节点if (pp == nullptr)root = q;else if (p == pp->leftChild)// 如果p是pp的左孩子pp->leftChild = q;else// 如果p是pp的右孩子pp->rightChild = q;// 如果s的父节点就是p,说明p节点的左子树只有左子树没有右子树// 那么删除p后pp就是其父节点if (ps == p) pp = q;else pp = ps;// 反之ps是其父节点delete p;p = s;}// p至多只有一个孩子// 把孩子的指针存放到cAVLTreeNode<pair<K, E> > *c;if (p->leftChild != nullptr)c = p->leftChild;elsec = p->rightChild;// 删除pif (p == root)root = c;else{// p是pp的左孩子还是右孩子if (p == pp->leftChild)pp->leftChild = c;else pp->rightChild = c;}treeSize--;delete p;// 调整平衡int bf = 0;bool isRoot = false;// 如果当前节点是根节点,当调整树之后,需要更新root指向的节点while(!st.empty()){p = st.top();st.pop();// 更新p节点的高度和其bf值if(p->leftChild != nullptr && p->rightChild != nullptr){p->height = max(p->leftChild->height, p->rightChild->height) + 1;bf = p->leftChild->height - p->rightChild->height;}else if(p->leftChild != nullptr){p->height = p->leftChild->height + 1;bf = p->leftChild->height;}else if(p->rightChild != nullptr){p->height = p->rightChild->height + 1;bf = 0 - p->rightChild->height;}else{p->height = 1;// 只有它自己bf = 0;}if(bf == 2) // 说明被删除节点在当前节点的右子树,是R型不平衡{// 计算当前节点左孩子的bf值int bfL = 0;// p的左孩子一定存在if(p->leftChild->leftChild != nullptr && p->leftChild->rightChild != nullptr)bfL = p->leftChild->leftChild->height - p->leftChild->rightChild->height;else if(p->leftChild->leftChild != nullptr)bfL = p->leftChild->leftChild->height;else if(p->leftChild->rightChild != nullptr)bfL = 0 - p->leftChild->rightChild->height;elsebfL = 0;// R0型if(bfL == 0){if(p == root)isRoot = true;rotateLL(p);if(isRoot)root = p;break;// 不用检查其父节点了}else if(bfL == 1)// R1型{if(p == root)isRoot = true;rotateLL(p);// 需要继续检查其父节点if(isRoot)root = p;}else if(bfL == -1)// R-1型{if(p == root)isRoot = true;if(p->leftChild->rightChild == nullptr)rotateLL(p);// 当当前节点的左孩子的右孩子为空时,找不到示意图中替换的C节点elserotateLR(p);//需要继续检查其父节点if(isRoot)root = p;}else{}// 其他,基本上不存在别的什么情况了}else if(bf == -2) // 说明被删除节点在当前节点的左子树,是L型不平衡{// 计算当前节点左孩子的bf值int bfR = 0;// p的右孩子一定存在if(p->rightChild->leftChild != nullptr && p->rightChild->rightChild != nullptr)bfR = p->rightChild->leftChild->height - p->rightChild->rightChild->height;else if(p->rightChild->leftChild != nullptr)bfR = p->rightChild->leftChild->height;else if(p->rightChild->rightChild != nullptr)bfR = 0 - p->rightChild->rightChild->height;elsebfR = 0;// L0型if(bfR == 0){if(p == root)isRoot = true;rotateRR(p);//需要继续检查其父节点if(isRoot)root = p;break;// 不用检查其父节点了}else if(bfR == 1)// L1型{if(p == root)isRoot = true;rotateRR(p);//需要继续检查其父节点if(isRoot)root = p;}else if(bfR == -1)// L-1型{if(p == root)isRoot = true;if(p->rightChild->leftChild == nullptr)rotateRR(p); // 当当前节点的右孩子的左孩子为空时,找不到示意图中替换的C节点elserotateRL(p);//需要继续检查其父节点if(isRoot)root = p;}else{}// 其他,基本上不存在别的什么情况了}else{}// 其他不操作}
}
// overload << for pair
template <class K, class E>
ostream& operator<<(ostream& out, const pair<K, E>& x)
{out << x.first << ":" << x.second; return out;}template <class K, class E>
ostream& operator<<(ostream& out, const AVLTreeNode<pair<K, E>>& x)
{out << x.element.first << ":" << x.element.second << " h = " << x.height; return out;}
#endif //_34BALANCED_SEARCH_TREE_AVLTREE_H
AVLTree.cpp
/*
Project name : _34Balanced_search_tree
Last modified Date: 2023年12月27日10点57分
Last Version: V1.0
Descriptions: AVL树测试函数
*/
#include "AVLTree.h"
#include<vector>void AVLTreeTest() {cout << "*************************AVLTreeTest() begin*******************************" << endl;AVLTree<int, char> y;pair<int, char> data(30, 'a');y.insert(data);data = pair<int, char>(35, 'e');y.insert(data);data = pair<int, char>(60, 'c');y.insert(data);data = pair<int, char>(5, 'b');y.insert(data);data = pair<int, char>(2, 'd');y.insert(data);data = pair<int, char>(80, 'f');y.insert(data);data = pair<int, char>(32, 'g');y.insert(data);data = pair<int, char>(85, 'h');y.insert(data);data = pair<int, char>(31, 'i');y.insert(data);data = pair<int, char>(33, 'j');y.insert(data);cout << "Tree size is " << y.size() << endl;cout << "Elements in ascending order are" << endl;y.inOrderOutput();pair<int, char> *s = y.find(60);cout << "Search for 60 succeeds " << endl;cout << s->first << ' ' << s->second << endl;y.erase(60);cout << "60 deleted " << endl;cout << "Tree size is " << y.size() << endl;cout << "Elements in ascending order are" << endl;y.inOrderOutput();s = y.find(80);cout << "Search for 80 succeeds " << endl;cout << s->first << ' ' << s->second << endl;y.erase(80);cout << "80 deleted " << endl;cout << "Tree size is " << y.size() << endl;cout << "Elements in ascending order are" << endl;y.inOrderOutput();s = y.find(30);cout << "Search for 30 succeeds " << endl;cout << s->first << ' ' << s->second << endl;y.erase(30);cout << "30 deleted " << endl;cout << "Tree size is " << y.size() << endl;cout << "Elements in ascending order are" << endl;y.inOrderOutput();s = y.find(35);cout << "Search for 35 succeeds " << endl;cout << s->first << ' ' << s->second << endl;y.erase(35);cout << "35 deleted " << endl;cout << "Tree size is " << y.size() << endl;cout << "Elements in ascending order are" << endl;y.inOrderOutput();s = y.find(2);cout << "Search for 2 succeeds " << endl;cout << s->first << ' ' << s->second << endl;y.erase(2);cout << "2 deleted " << endl;cout << "Tree size is " << y.size() << endl;cout << "Elements in ascending order are" << endl;y.inOrderOutput();s = y.find(32);cout << "Search for 32 succeeds " << endl;cout << s->first << ' ' << s->second << endl;y.erase(32);cout << "32 deleted " << endl;cout << "Tree size is " << y.size() << endl;cout << "Elements in ascending order are" << endl;y.inOrderOutput();s = y.find(5);cout << "Search for 5 succeeds " << endl;cout << s->first << ' ' << s->second << endl;y.erase(5);cout << "5 deleted " << endl;cout << "Tree size is " << y.size() << endl;cout << "Elements in ascending order are" << endl;y.inOrderOutput();cout << "***************************AVLTreeTest() end*******************************" << endl;
}
AVLTreeNode.h
/*
Project name : _34Balanced_search_tree
Last modified Date: 2023年12月27日10点57分
Last Version: V1.0
Descriptions: AVL树节点模板类
*/#ifndef _34BALANCED_SEARCH_TREE_AVLTREENODE_H
#define _34BALANCED_SEARCH_TREE_AVLTREENODE_Htemplate<class T>
struct AVLTreeNode {T element;AVLTreeNode<T> *leftChild, // 左子树*rightChild; // 右子树// 记录height即可,需要bf的值可以根据height来计算,但是bf值本身没有特别的意义,只是为了方便分析各种不平衡的情况int height;AVLTreeNode() {leftChild = rightChild = nullptr;height = 0;}explicit AVLTreeNode(T &theElement) : element(theElement) {leftChild = rightChild = nullptr;height = 0;}explicit AVLTreeNode(T &theElement,AVLTreeNode *theLeftChild,AVLTreeNode *theRightChild): element(theElement), leftChild(theLeftChild), rightChild(theRightChild) {height = 0;}explicit AVLTreeNode(T &theElement,AVLTreeNode *theLeftChild,AVLTreeNode *theRightChild, int theHeight): element(theElement), leftChild(theLeftChild), rightChild(theRightChild) {height = theHeight;}
};#endif //_34BALANCED_SEARCH_TREE_AVLTREENODE_H
dictionary.h
/*
Project name : _33Search_tree
Last modified Date: 2023年12月21日11点13分
Last Version: V1.0
Descriptions: 字典虚基类
*/#ifndef _33SEARCH_TREE_DICTIONARY_H
#define _33SEARCH_TREE_DICTIONARY_H
#include <iostream>
#include <utility>using namespace std;template<class K, class E>
class dictionary
{
public:virtual ~dictionary() = default;[[nodiscard]] virtual bool empty() const = 0;// 如果字典为空则返回true,反之返回false[[nodiscard]] virtual int size() const = 0;// 返回字典中有多少个pairvirtual pair<K, E>* find(K) const = 0;// 根据键值返回pair的指针virtual void erase(K) = 0;// 根据键值移除pair元素virtual void insert(pair<K, E>&) = 0;// 插入一个(key, value)pair到字典中
};
#endif //_33SEARCH_TREE_DICTIONARY_H
main.cpp
#include <iostream>
#include "AVLTree.h"int main() {AVLTreeTest();return 0;
}
运行结果
"C:\Users\15495\Documents\Jasmine\prj\_Algorithm\Data Structures, Algorithms and Applications in C++\_34Balanced search tree\cmake-build-debug\_34Balanced_search_tree.exe"
*************************AVLTreeTest() begin*******************************
Tree size is 10
Elements in ascending order are
2:d h = 1
5:b h = 2
30:a h = 1
31:i h = 3
32:g h = 2
33:j h = 1
35:e h = 4
60:c h = 1
80:f h = 2
85:h h = 1Search for 60 succeeds
60 c
60 deleted
Tree size is 9
Elements in ascending order are
2:d h = 1
5:b h = 2
30:a h = 1
31:i h = 3
32:g h = 2
33:j h = 1
35:e h = 4
80:f h = 2
85:h h = 1Search for 80 succeeds
80 f
80 deleted
Tree size is 8
Elements in ascending order are
2:d h = 1
5:b h = 2
30:a h = 1
31:i h = 4
32:g h = 2
33:j h = 1
35:e h = 3
85:h h = 1Search for 30 succeeds
30 a
30 deleted
Tree size is 7
Elements in ascending order are
2:d h = 1
5:b h = 2
31:i h = 4
32:g h = 2
33:j h = 1
35:e h = 3
85:h h = 1Search for 35 succeeds
35 e
35 deleted
Tree size is 6
Elements in ascending order are
2:d h = 1
5:b h = 2
31:i h = 4
32:g h = 1
33:j h = 3
85:h h = 1Search for 2 succeeds
2 d
2 deleted
Tree size is 5
Elements in ascending order are
5:b h = 1
31:i h = 2
32:g h = 1
33:j h = 3
85:h h = 1Search for 32 succeeds
32 g
32 deleted
Tree size is 4
Elements in ascending order are
5:b h = 1
31:i h = 2
33:j h = 3
85:h h = 1Search for 5 succeeds
5 b
5 deleted
Tree size is 3
Elements in ascending order are
31:i h = 1
33:j h = 2
85:h h = 1***************************AVLTreeTest() end*******************************Process finished with exit code 0
相关文章:

《数据结构、算法与应用C++语言描述》- 平衡搜索树 -全网唯一完整详细实现插入和删除操作的模板类
平衡搜索树 完整可编译运行代码见:Github::Data-Structures-Algorithms-and-Applications/_34Balanced search tree 概述 本章会讲AVL、红-黑树、分裂树、B-树。 平衡搜索树的应用? AVL 和红-黑树和分裂树适合内部存储的应用。 B-树适合外部存储的…...

网络路由跟踪工具
随着企业网络需求的增长,组织发现监控和管理其网络基础设施变得越来越困难。网络管理员正在转向其他工具和资源,这些工具和资源可以使他们的工作更轻松一些,尤其是在故障排除方面。 目前,网络管理员主要使用简单、免费提供的实用…...

设计模式 七大原则
1.单一职责原则 单一职责原则(SRP:Single responsibility principle)又称单一功能原则 核心:解耦和增强内聚性(高内聚,低耦合)。 描述: 类被修改的几率很大,因此应该专注…...

(1)(1.13) SiK无线电高级配置(一)
文章目录 前言 1 监控链接质量 2 诊断范围问题 3 MAVLink协议说明 前言 本文提供 SiK 遥测无线电(SiK Telemetry Radio)的高级配置信息。它面向"高级用户"和希望更好地了解无线电如何运行的用户。 !Tip 大多数用户只需要 SiK Radio v2 中提供的基本…...
drf知识--10
接口文档 # 后端把接口写好后: 登录接口:/api/v1/login ---> post---name pwd 注册接口 查询所有图书带过滤接口 # 前后端需要做对接,对接第一个东西就是这个接口文档,前端照着接口文档开发 公司3个人ÿ…...

探索 Vue 实例方法的魅力:提升 Vue 开发技能(下)
🤍 前端开发工程师(主业)、技术博主(副业)、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云…...
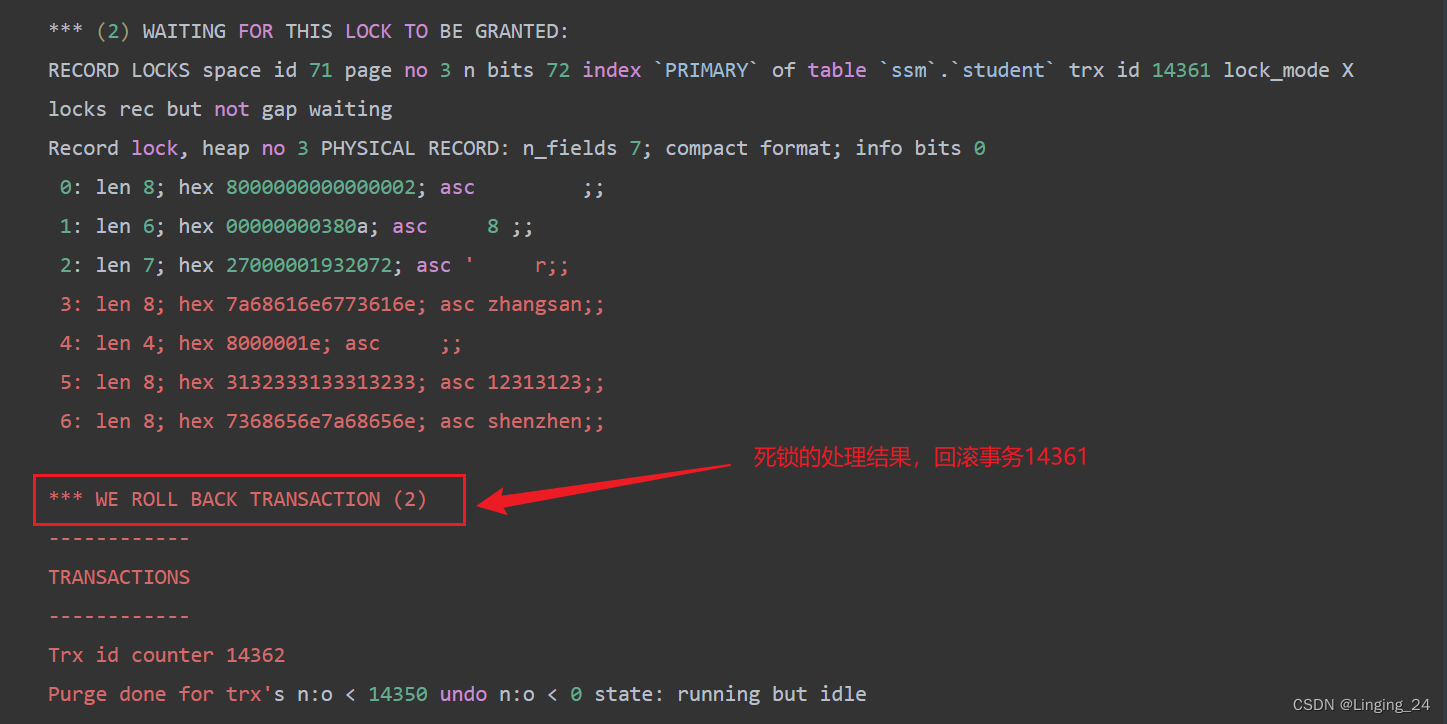
mysql死锁排查
查看正在进行中的事务 SELECT * FROM information_schema.INNODB_TRX;字段解释trx_id唯一事务id号,只读事务和非锁事务是不会创建id的trx_state事务的执行状态,值一般分为:RUNNING, LOCK WAIT, ROLLING BACK, and COMMITTING.trx_started事务…...
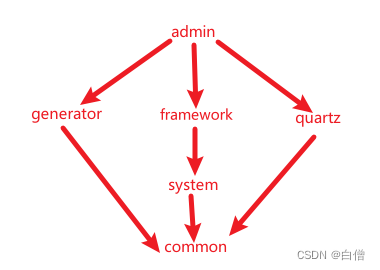
若依项目(ruoy-vue)多模块依赖情况简要分析
主pom文件关键点分析 properties标签声明变量信息:版本号、编码类型、java版本spring-boot依赖形式:spring-boot-dependencies、pom、importdependencies中添加本项目内部模块,同时在modules中声明模块packaging打包选择pom设置打包maven-co…...

【普中开发板】基于51单片机的篮球计分器液晶LCD1602显示( proteus仿真+程序+设计报告+讲解视频)
基于普中开发板51单片机的篮球计分器液晶LCD1602显示 1.主要功能:讲解视频:2.仿真3. 程序代码4. 设计报告5. 设计资料内容清单&&下载链接资料下载链接(可点击): 基于51单片机的篮球计分器液晶LCD1602显示 ( pr…...

按照层次遍历结果打印完全二叉树
按照层次遍历结果打印完全二叉树 按照推论结果: l 层首个节点位置 2h-l - 1l 层节点间距:2h-l1 - 1 编码实现 public static<E> void print(BinaryTree<E> tree) {List<List<Node<E>>> levelNodeList levelOrderTraver…...

基于SpringBoot的药店管理系统
文章目录 项目介绍主要功能截图:部分代码展示设计总结项目获取方式🍅 作者主页:超级无敌暴龙战士塔塔开 🍅 简介:Java领域优质创作者🏆、 简历模板、学习资料、面试题库【关注我,都给你】 🍅文末获取源码联系🍅 项目介绍 基于SpringBoot的药店管理系统,java项目…...
Java 泛型深入解析
Java 中的泛型是一种强大的编程特性,允许我们编写更加通用和类型安全的代码。本篇博客将深入探讨 Java 泛型的各个方面,包括泛型类、泛型方法、泛型接口以及泛型通配符。 1. 泛型类 首先,让我们看一个简单的泛型类的例子。在下面的代码中&a…...

Apache Doris (六十): Doris - 物化视图
🏡 个人主页:IT贫道_大数据OLAP体系技术栈,Apache Doris,Clickhouse 技术-CSDN博客 🚩 私聊博主:加入大数据技术讨论群聊,获取更多大数据资料。 🔔 博主个人B栈地址:豹哥教你学编程的个人空间-豹哥教你学编程个人主页-哔哩哔哩视频 目录...

【javaweb】tomcat9.0中的HttpServlet
2023年12月28日,周四晚上 目录 什么是HttpServlet tomcat中的HttpServlet由谁产生 什么是HttpServlet 在Tomcat中,HttpServlet 是 Java Servlet API 中的一个抽象类,用于简化基于HTTP协议的Servlet的开发。HttpServlet 扩展了 GenericServ…...
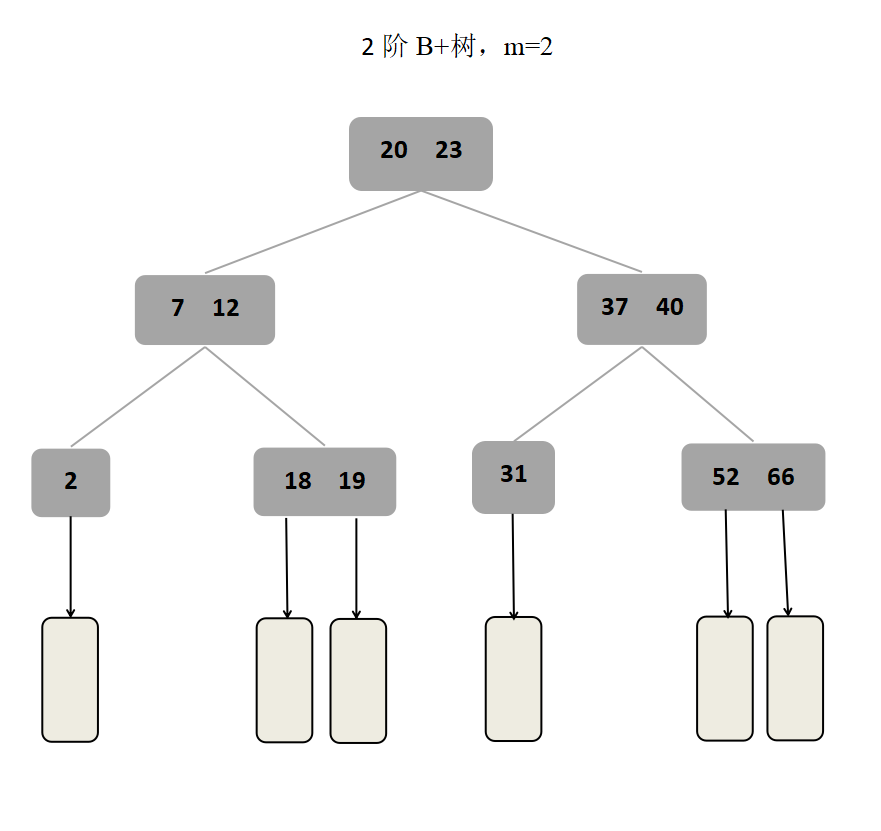
数据结构学习笔记——查找算法中的树形查找(B树、B+树)
目录 前言一、B树(一)B树的概念(二)B树的性质(三)B树的高度(四)B树的查找(五)B树的插入(六)B树的删除 二、B树(一…...
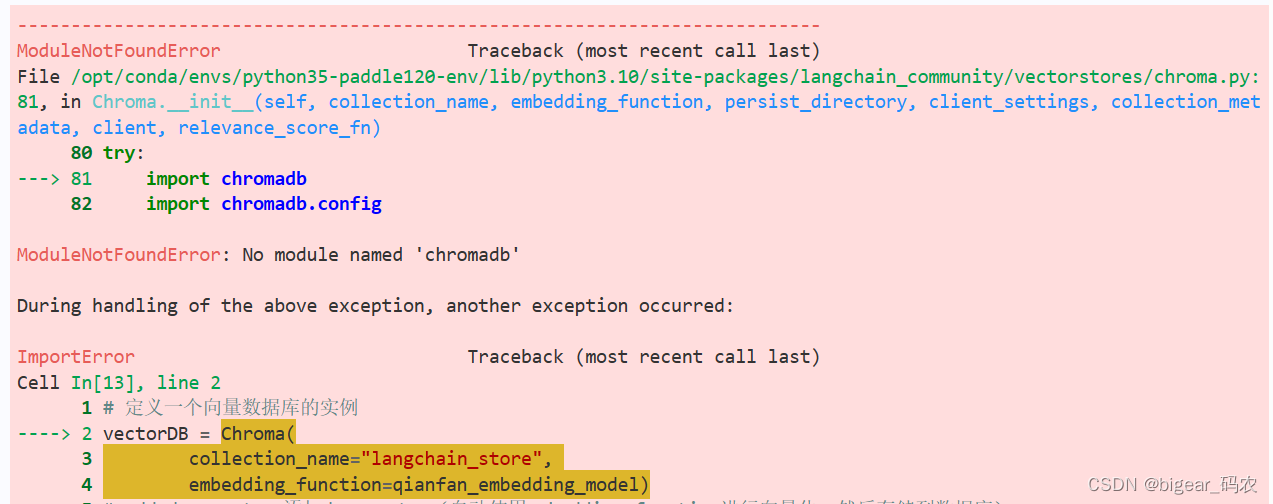
python包chromadb安装失败总结
1,背景: 最近在学习langchain的课程,里面创建自己的知识库的Retrieval模块中,需要用到向量数据库。 所以按照官方的教程(vectorstores),准备使用chroma的向量数据库。图片来源 2,问…...

机器学习(四) -- 模型评估(2)
系列文章目录 机器学习(一) -- 概述 机器学习(二) -- 数据预处理(1-3) 机器学习(三) -- 特征工程(1-2) 机器学习(四) -- 模型评估…...

泊松分布与二项分布的可加性
泊松分布与二项分布的可加性 泊松分布的可加性 例 : 设 X , Y X,Y X,Y 相互独立 , X ∼ P ( λ 1 ) X\sim P(\lambda_1) X∼P(λ1) , Y ∼ P ( λ 2 ) Y\sim P(\lambda_2) Y∼P(λ2) , 求证 Z X Y ZXY ZXY 服从参数为 λ 1 λ 2 \lambda_1 \lambda_2 λ1λ2 …...

【PostgreSQL】约束-排他约束
【PostgreSQL】约束链接 检查 唯一 主键 外键 排他 排他约束 排他约束是一种数据库约束,用于确保某一列或多个列中的值在每一条记录中都是唯一的。这意味着任何两条记录都不能具有相同的值。 排他约束可以在数据库中创建唯一索引或唯一约束来实现。当尝试插入或更…...

Java重修第一天—学习数组
1. 认识数组 建议1.5倍速学习,并且关闭弹幕。 数组的定义:数组是一个容器,用来存储一批同种类型的数据。 下述图:是生成数字数组和字符串数组。 为什么有了变量还需要定义数组呢?为了解决在某些场景下,变…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

ubuntu22.04 安装docker 和docker-compose
首先你要确保没有docker环境或者使用命令删掉docker sudo apt-get remove docker docker-engine docker.io containerd runc安装docker 更新软件环境 sudo apt update sudo apt upgrade下载docker依赖和GPG 密钥 # 依赖 apt-get install ca-certificates curl gnupg lsb-rel…...

客户案例 | 短视频点播企业海外视频加速与成本优化:MediaPackage+Cloudfront 技术重构实践
01技术背景与业务挑战 某短视频点播企业深耕国内用户市场,但其后台应用系统部署于东南亚印尼 IDC 机房。 随着业务规模扩大,传统架构已较难满足当前企业发展的需求,企业面临着三重挑战: ① 业务:国内用户访问海外服…...

欢乐熊大话蓝牙知识17:多连接 BLE 怎么设计服务不会乱?分层思维来救场!
多连接 BLE 怎么设计服务不会乱?分层思维来救场! 作者按: 你是不是也遇到过 BLE 多连接时,调试现场像网吧“掉线风暴”? 温度传感器连上了,心率带丢了;一边 OTA 更新,一边通知卡壳。…...

Cursor AI 账号纯净度维护与高效注册指南
Cursor AI 账号纯净度维护与高效注册指南:解决限制问题的实战方案 风车无限免费邮箱系统网页端使用说明|快速获取邮箱|cursor|windsurf|augment 问题背景 在成功解决 Cursor 环境配置问题后,许多开发者仍面临账号纯净度不足导致的限制问题。无论使用 16…...
