【计算机算法设计与分析】n皇后问题(C++_回溯法)
文章目录
- 题目描述
- 测试样例
- 算法原理
- 算法实现
- 参考资料
题目描述
在nxn格的棋盘上放置彼此不受攻击的n格皇后。按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。n后问题等价于在nxn格的棋盘上放置n个皇后,任何2个皇后不放在同一行或同一列或同一斜线上。
当n=6时,一个如下的 6×6 的跳棋棋盘:

上面的布局可以用序列 2 4 6 1 3 5 来描述,第 i 个数字表示在第 i 行的相应位置有一个棋子。这只是棋子放置的一个解。请编一个程序找出所有棋子放置的解。并把它们以上面的序列方法输出,解按字典顺序排列。请输出前三个解。最后一行是解的总个数。
测试样例
输入:
6
输出:
2 4 6 1 3 5
3 6 2 5 1 4
4 1 5 2 6 3
4
算法原理
使用回溯法对解空间进行深度优先搜索遍历,同时要满足规则(任何两个皇后不放在同一行或同一列或同一斜线上),为节省时间我创建了四个数组:x[1000], y[1000], zr[1000], zl[1000],分别存储横轴、纵轴、左对角线、右对角线上是否已被占用的信息。其中,x[i]=j表示在第i行第j个位置放置一个皇后(方便输出结果);y[j]=1表示第j列已被占用;zr[i - j + n]=1表示这条从左上到右下的对角线已被占用(所有处于同一条左上到右下对角线上元素的横坐标减纵坐标都相同,为了让索引为正,所以加n);zl[i+j]=1表示这条从右上到左下的对角线已被占用(所有处于同一条右上到左下对角线上元素的横坐标加纵坐标都相同)。
算法实现
#include<bits/stdc++.h>
using namespace std;int n, num = 0;
int x[1000], y[1000], zr[1000], zl[1000];
void print()
{if (num < 3){for (int i = 1; i <= n; i++)cout << x[i] << " ";cout << endl;}num++;
}
void dfs(int i)
{if (i > n){print();return;}else{for (int j = 1; j <= n; j++){if ((!y[j]) && (!zr[i - j + n]) && (!zl[i + j])){x[i] = j;//i行第j个y[j] = 1;zr[i - j + n] = 1;zl[i + j] = 1;dfs(i + 1);//递归y[j] = 0;zr[i - j + n] = 0;zl[i + j] = 0;}}}
}
int main()
{cin >> n;dfs(1);cout << num;return 0;
}
参考资料
回溯法之n皇后问题总结_用回溯法求解n皇后问题的思路
相关文章:

【计算机算法设计与分析】n皇后问题(C++_回溯法)
文章目录 题目描述测试样例算法原理算法实现参考资料 题目描述 在nxn格的棋盘上放置彼此不受攻击的n格皇后。按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。n后问题等价于在nxn格的棋盘上放置n个皇后,任何2个皇后不放在同…...

Calendar日历类型常见方法
Calendar日历类型常见方法: 概括:1.get( )方法2、set( ) 设置时间3、常用的add方法4、after()方法表示的时间是否在指定时间之后, before( ) 方法则之前, 返回判断结果4.1、compareTo比较器 概括: Calendar类是一个抽…...

Docker-Compose部署Redis(v7.2)主从模式
文章目录 一、前提准备1. redis配置文件2. 下载redis镜像3. 文件夹结构 二、docker-compose三、主从配置1.主节点配置文件2.从节点配置文件 四、运行五、测试 环境 docker desktop for windows 4.23.0redis 7.2 一、前提准备 1. redis配置文件 因为Redis 7.2 docker镜像里面…...
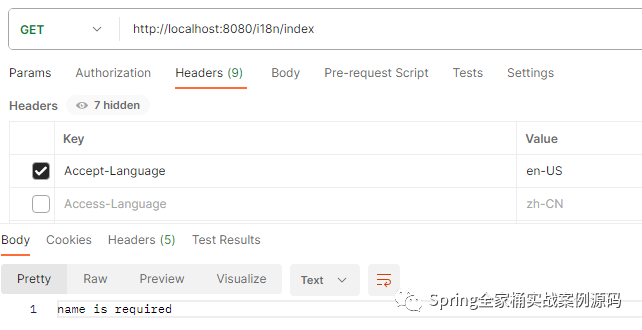
Spring国际化的应用及原理详解
1. 简介 Spring国际化(Spring Internationalization,简称i18n)是Spring框架提供的一种机制,用于支持多语言的应用程序。它使得开发者能够轻松地在应用程序中实现不同语言的支持,从而满足全球化的需求。通过Spring国际…...

Existing installation is up to date
这个报错是之前安装的docker没有删除干净 解决方法: 打开注册表编辑器 然后再搜索栏:HKEY_LOCAL_MACHINE\SOFTWARE\Microsoft\Windows\CurrentVersion\Uninstall\Docker Desktop 回车 找到Docker Desktop文件夹后,右键删除 重新安装Docker…...
windows安装kafka以及kafka管理工具推荐
windows安装 1.下载地址 下载地址 下载最新版本的.tgz文件解压 2.修改配置 修改config目录下的zookeeper.properties中的dataDir属性 server.properties文件中的log.dir属性 3.启动zookeeper 进入到bin\windows\下的用cmd输入zookeeper-server-start.bat ..\..\config\zo…...
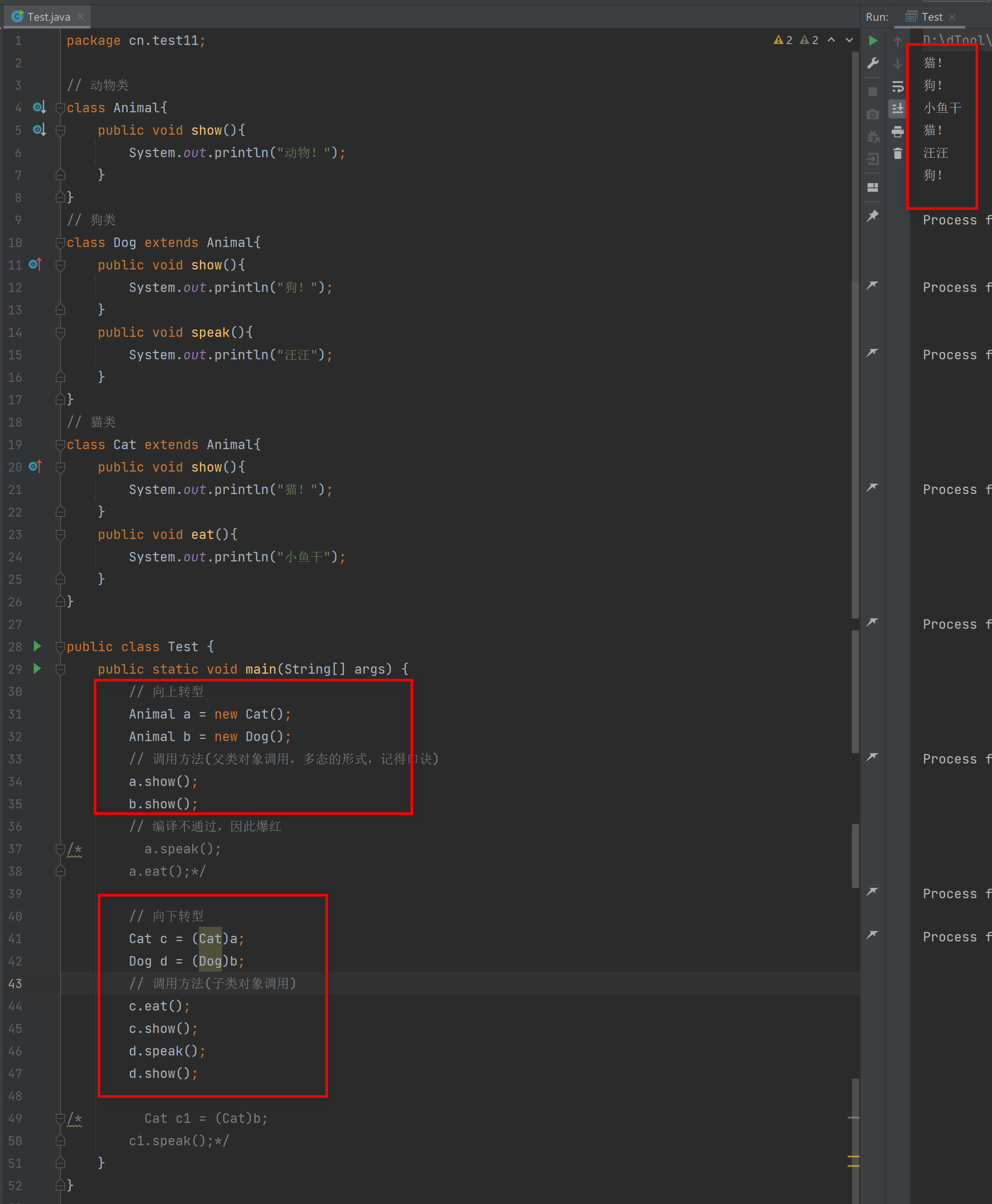
面向对象的三大特征之一多态
多态 概念 多态是同一个对象,在不同时刻表现出来不同的形态,称之为多态。 例如:水,我们把水理解成为一个对象,而水会有不同的形态,比如 液态水、冰块、水蒸气 多态的前提 有继承/实现关系(继承…...
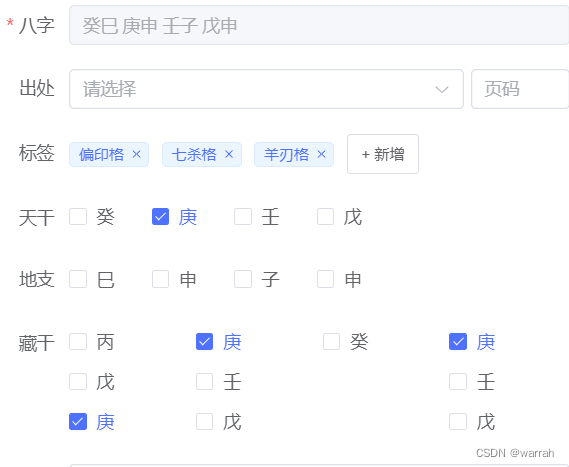
vue3中标签form插件
想写一个系统,对八字进行标注,比如格局,有些八字就有很多格局,于是就想着使用el-tag但是,form表单中如何处理呢? 这个时候,就需要自己写一个,modelValue是表单的默认属性 <template><…...
企业数字化转型:1个核心、2种力量、3个关键点、4大转型、5大平台
引言 企业数字化转型源于当今数字化时代的巨大变革。随着科技的飞速发展和全球市场的日益竞争,企业们正面临着前所未有的挑战和机遇。这些挑战包括消费者行为的变化、新技术的涌现以及市场竞争的加剧。在这种环境下,传统的商业模式和运营方式已经不再适…...

Agilent安捷伦E4990A阻抗分析仪20Hz
Agilent安捷伦E4990A阻抗分析仪性能卓越,适用于元器件、半导体和材料测量。它具有宽广的频率范围,从20Hz到120MHz,能够适应各种不同的阻抗测量需求。在宽阻抗范围内,该仪器能够提供出色的0.045%(典型值)基本…...
性能优化-OpenMP概述(一)-宏观全面理解OpenMP
本文旨在从宏观角度来介绍OpenMP的原理、编程模型、以及在各个领域的应用、使用、希望读者能够从本文整体上了解OpenMP。 🎬个人简介:一个全栈工程师的升级之路! 📋个人专栏:高性能(HPC)开发基础…...
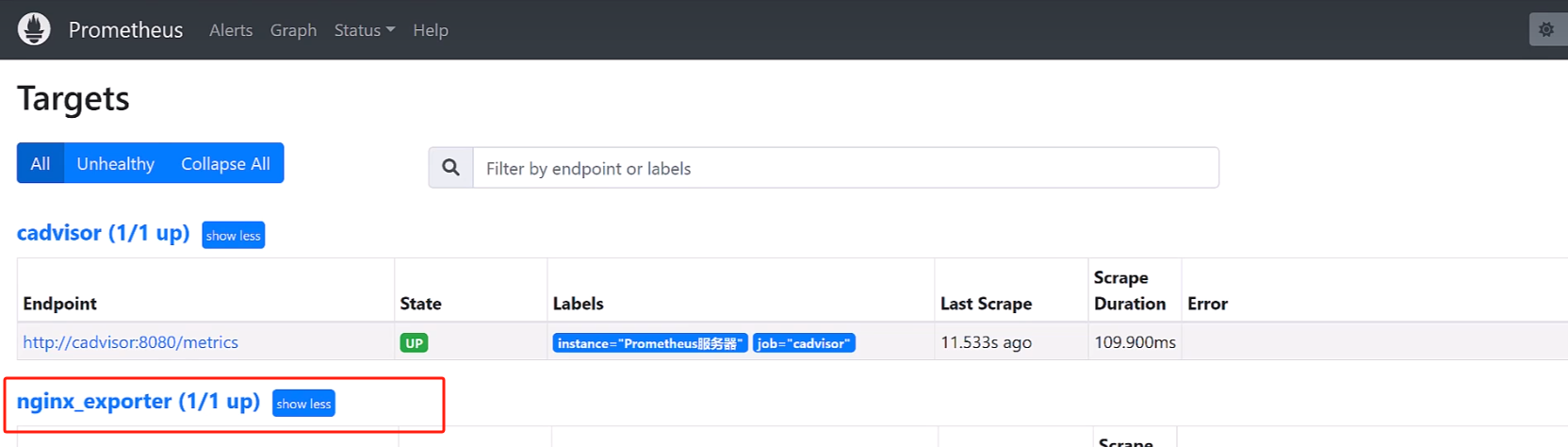
Prometheus实战篇:Prometheus监控nginx
准备环境 在此专栏的前几篇文章中已经准备了一台服务器作为我们进行环境的准备.大家也可以通过虚拟机创建俩台服务器,一台作为Prometheus的安装另外一台进行其他软件安装并且进行监控的服务器. 这里我就不赘述nginx的安装教程,相信大家都可以搜到,使用docker或者直接通过安装包…...

JVM加载class文件的原理机制
1、JVM 简介 JVM 是我们Javaer 的最基本功底了,刚开始学Java 的时候,一般都是从“Hello World ”开始的,然后会写个复杂点class ,然后再找一些开源框架,比如Spring ,Hibernate 等等,再然后就开发…...

如何使用CapSolver解决Web爬虫中遇到的CAPTCHA问题
Web爬取是一种强大的技术,用于从网站中提取数据,但经常会遇到一个常见障碍,即CAPTCHA。CAPTCHA是“Completely Automated Public Turing test to tell Computers and Humans Apart”的缩写,旨在防止自动机器人访问网站。然而&…...

杰发科技AC7801——IO模拟IIC注意事项
7801的参考手册没有说清楚 7840说明了用开漏 使用办法...

展台搭建与设计都有哪些思路
1、现代简约 设计理念强调简洁、线条清晰和空间布局,突出产品本身,使展台干净整洁,适合展示高科技、现代化的产品。 2、自然生态 利用植物、木材等自然元素,营造与自然和谐共处的氛围,适合健康、环保、生态产品。 3、品…...

解决mock单元测试中 无法获取实体类xxx对应的表名
错误描述:在执行单元测试时,执行到new Example时抛出异常,提示无法获取实体类xxx对应的表名 Example example new Example(ServeSubscribeRecord.class);Example.Criteria criteria example.createCriteria();criteria.andEqualTo("se…...

arm64虚拟化技术与kvm实现原理分享
文章目录 1 简介2 arm64 虚拟化相关硬件支持2.1 arm64 cpu 虚拟化基本原理及硬件支持2.2 系统寄存器捕获和虚拟寄存器支持2.3 VHE 特性支持2.4 内存虚拟化支持2.5 IO 虚拟化支持2.6 DMA 虚拟化支持2.7 中断虚拟化支持2.8 定时器虚拟化支持 3 arm64 kvm 初始化流程3.1 初始化总体…...

选择 省市区 组件数据 基于vue3 + elment-plus
h5 <el-cascader v-model"form.area" :props"{value: label,label: label }" :options"jsonData" change"handleChange" style"width: 100%;" /> script import jsonData from /utils/city.json; 选完省市区 数据是一…...

了解 nextTick
一. 什么是 nextTick 简单的说,nextTick 方法是在 Vue.js 中常见的一种异步更新 DOM 的机制。它的原理是利用 JavaScript 的事件循环机制以及浏览器的渲染流程来实现延迟执行 DOM 更新操作。 它的出现主要是为了解决 Vue 的异步更新导致的 DOM 更新后的操作问题。…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...
