算法每日一题:队列中可以看到的人数 | 单调栈
大家好,我是星恒
今天是一道困难题,他的题解比较好理解,但是不好想出来,接下来就让我带大家来捋一捋这道题的思路,以及他有什么特征
题目:leetcode 1944
有 n 个人排成一个队列,从左到右 编号为 0 到 n - 1 。给你以一个整数数组 heights ,每个整数 互不相同,heights[i] 表示第 i 个人的高度。
一个人能 看到 他右边另一个人的条件是这两人之间的所有人都比他们两人 矮 。更正式的,第 i 个人能看到第 j 个人的条件是 i < j 且 min(heights[i], heights[j]) > max(heights[i+1], heights[i+2], …, heights[j-1]) 。
请你返回一个长度为 n 的数组_ answer ,其中 answer[i] _是第 i 个人在他右侧队列中能 看到 的 人数 。
示例:
示例 1:
输入:heights = [10,6,8,5,11,9]
输出:[3,1,2,1,1,0]
解释:
第 0 个人能看到编号为 1 ,2 和 4 的人。
第 1 个人能看到编号为 2 的人。
第 2 个人能看到编号为 3 和 4 的人。
第 3 个人能看到编号为 4 的人。
第 4 个人能看到编号为 5 的人。
第 5 个人谁也看不到因为他右边没人。
示例 2:
输入:heights = [5,1,2,3,10]
输出:[4,1,1,1,0]
提示:
- n == heights.length
- 1 <= n <= 105
- 1 <= heights[i] <= 105
- heights 中所有数 互不相同 。
分析:
看到这道题,大家第一想到的一定是枚举每一种情况,然后依次与每一个值比较,记录比当前值大的值;当然,他的时间复杂度是O(n2),他的作用只能是为我们提供一些信息:
最大都是O(n2),说明优化大概率是O(n) 或者 O(nlogn);我们可以想到的方法,二分?利用一些特殊的数据结构?动归?等等。很明显这道题不能使用二分,因为没有折半的判断条件呀!所以我们可以拓展其他思维
从题目中的例子可以看出,对于某个人,他可以看到 比它小的人,并且这些人的规律是 单调递增,ok,看到单调性,我们肯定能想到这个数据结构:单调栈,没错,这道题的思路就是单调栈,但难点就在如何使用单调栈:
由于前面的看到的是一个单调递增的序列,并且我们需要从后向前来维护,所以我们维护一个从栈底到栈顶递减的一个栈。
同样,由于前面的人,看不到被后面的人挡住的比其(后面的这个人)小的人,即使这个人比它小,所以我们可以直接把他抛弃掉,这样前面的人只要将栈里面比它小的人统计,就可以知道它可以看多少人了,当然,统计后出栈即可,因为它挡住了前面的视线(看比它小的人的视线)
题解:
class Solution {public int[] canSeePersonsCount(int[] heights) {int n = heights.length;Deque<Integer> stack = new ArrayDeque<Integer>();int[] res = new int[n];for (int i = n - 1; i >= 0; i--) {int h = heights[i];while (!stack.isEmpty() && stack.peek() < h) {stack.pop();res[i]++;}if (!stack.isEmpty()) {res[i]++;}stack.push(h);}return res;}
}
如果大家有什么思考和问题,可以在评论区讨论,也可以私信我,很乐意为大家效劳。
好啦,今天的每日一题到这里就结束了,如果大家觉得有用,可以可以给我一个小小的赞呢,我们下期再见!
这里和大家说声不好意思,这周从元旦开始都没有发帖子,尤其每日一题,对不起!
原因是这今天都计划上午写贴子,晚上发贴子,但是由于这几天回了家里,稍微有点忙,并且和在学校相比,有些许不适应,所以一直没有顾上发,但其实我每天都在坚持写,今天我们把我这周攒下的每日一题都发出来了,大家感兴趣的可以去看看,让我们一起进步 ~~~
相关文章:

算法每日一题:队列中可以看到的人数 | 单调栈
大家好,我是星恒 今天是一道困难题,他的题解比较好理解,但是不好想出来,接下来就让我带大家来捋一捋这道题的思路,以及他有什么特征 题目:leetcode 1944有 n 个人排成一个队列,从左到右 编号为 …...

报表控件Stimulsoft 2023回顾:都做了哪些产品的改变?
在2023年过去一年中,报表控件Stimulsoft 针各类控件都做了重大改变,其中新增了某些产品、同时加强了很多产品的性能和UI设计,更加符合开发者需求,下面就跟随小编一起来回顾,具体都有哪些↓↓↓ Stimulsoft Ultimate &…...
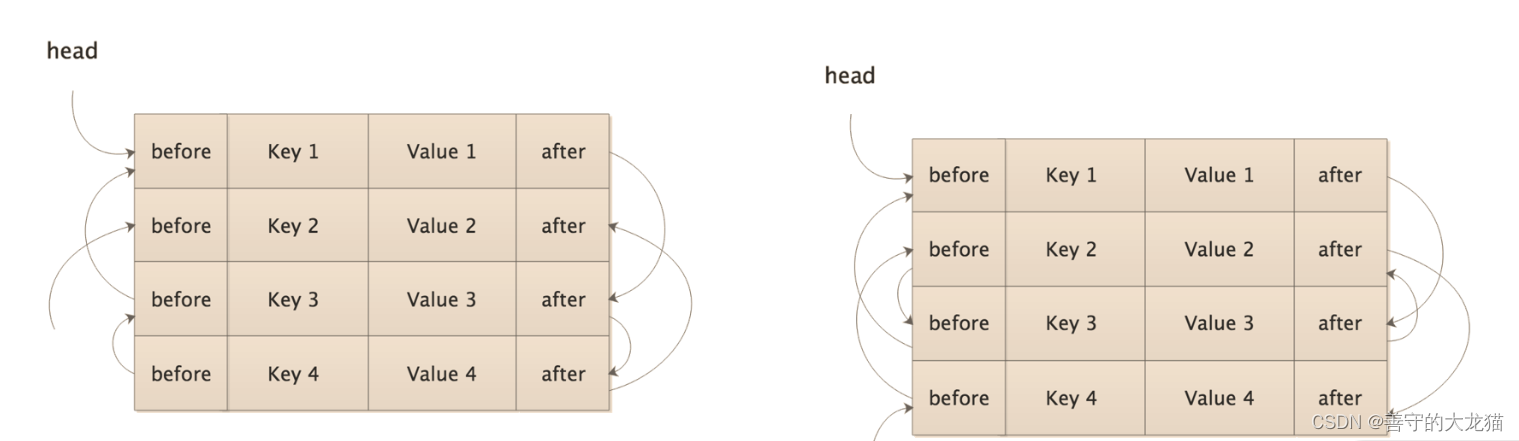
Mybatis缓存实现方式
文章目录 装饰器模式Cache 接口及核心实现Cache 接口装饰器1. BlockingCache2. FifoCache3. LruCache4. SoftCache5. WeakCache 小结 缓存是优化数据库性能的常用手段之一,我们在实践中经常使用的是 Memcached、Redis 等外部缓存组件,很多持久化框架提供…...
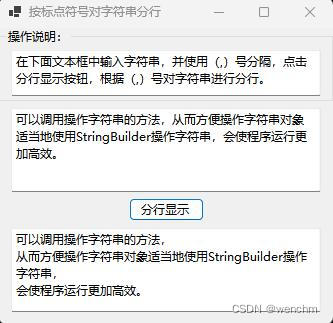
C#用StringBuilder高效处理字符串
目录 一、背景 二、使用StringBuilder便捷、高效地操作字符串 三、实例 1.源码 2.生成效果 四、实例中知识点 1.StringBuilder 构造函数 (1)定义 (2)重载 (3)StringBuilder() (4&…...
答案(4.2))
python开发案例教程-清华大学出版社(张基温)答案(4.2)
目录 练习 4.2 1. 代码分析题 2. 程序设计题 练习 4.2 1. 代码分析题 阅读下面的代码,给出输出结果。 (1) class A:def __init__(self,a,b,c):self.xabca A(3,5,7);b getattr(a,x);setattr(a,x,b3);print(a.x)18 (2&…...
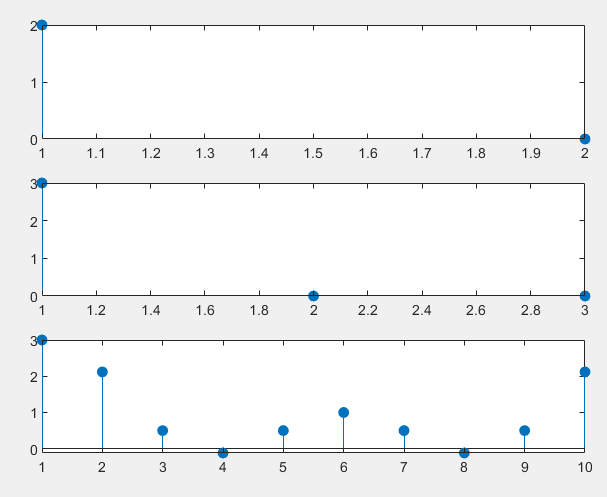
【MATLAB】【数字信号处理】线性卷积和抽样定理
已知有限长序列:xk1,2,1,1,0,-3, hk[1,-1,1] , 计算离散卷积和ykxk*h(k) 。 程序如下: function [t,x] My_conv(x1,x2,t1,t2,dt) %文件名与函数名对应 %自写的卷积函数 x conv(x1,x2)*dt; t0 t1(1) t2(1); L length(x1) length(x2)-2; t t0:dt…...

什么是 MVVM ?
课堂笔记 什么是 MVVM ? MVVM 是一种架构模式,它最初是由微软的两位工程师在 2005 年的时候所提出的。 Model:Model代表的是你的数据View:视图,直接和用户打交道的ViewModel:ViewModel 是 View 和 Model…...
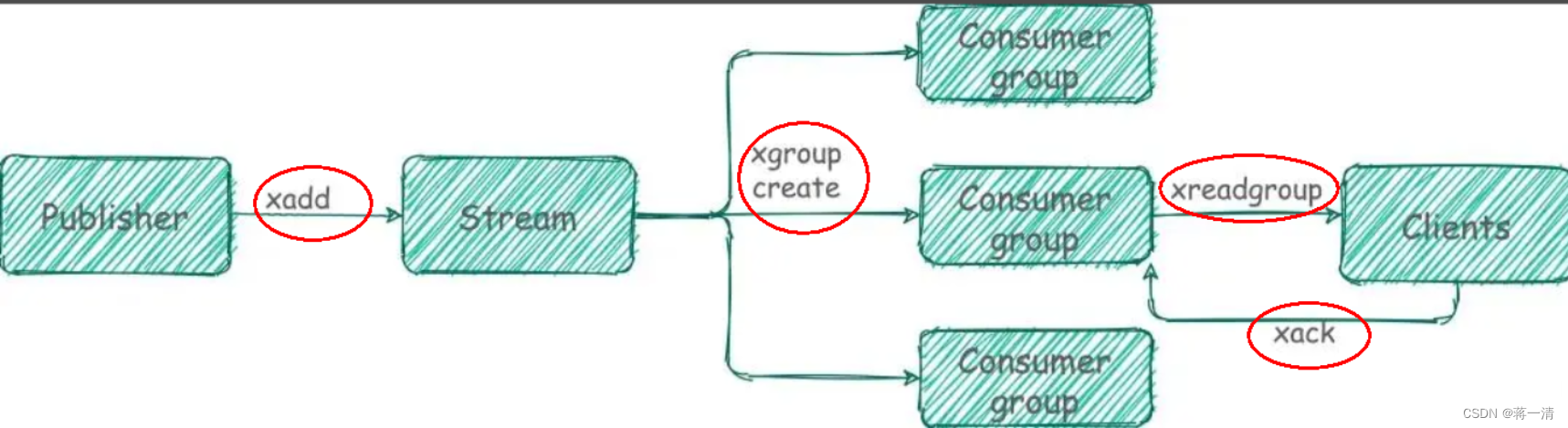
Redis(一)
1、redis Redis是一个完全开源免费的高性能(NOSQL)的key-value数据库。它遵守BSD协议,使用ANSI C语言编写,并支持网络和持久化。Redis拥有极高的性能,每秒可以进行11万次的读取操作和8.1万次的写入操作。它支持丰富的数…...
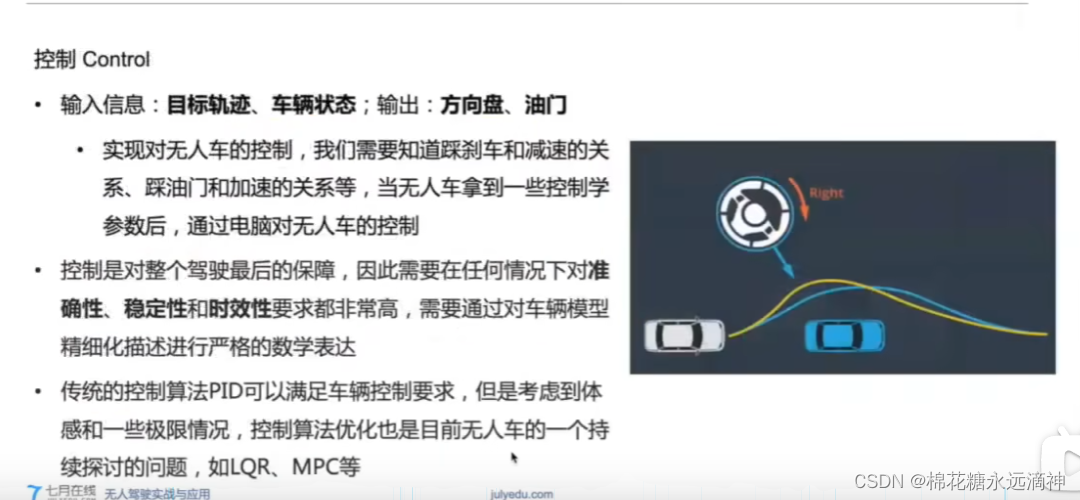
自动驾驶预测-决策-规划-控制学习(1):自动驾驶框架、硬件、软件概述
文章目录 前言:无人驾驶分级一、不同level的无人驾驶实例分析1.L2级别2.L3级别3.L4级别①如何在减少成本的情况下,实现类似全方位高精度的感知呢?②路侧终归是辅助,主车的智能才是重中之重:融合深度学习 二、无人驾驶的…...
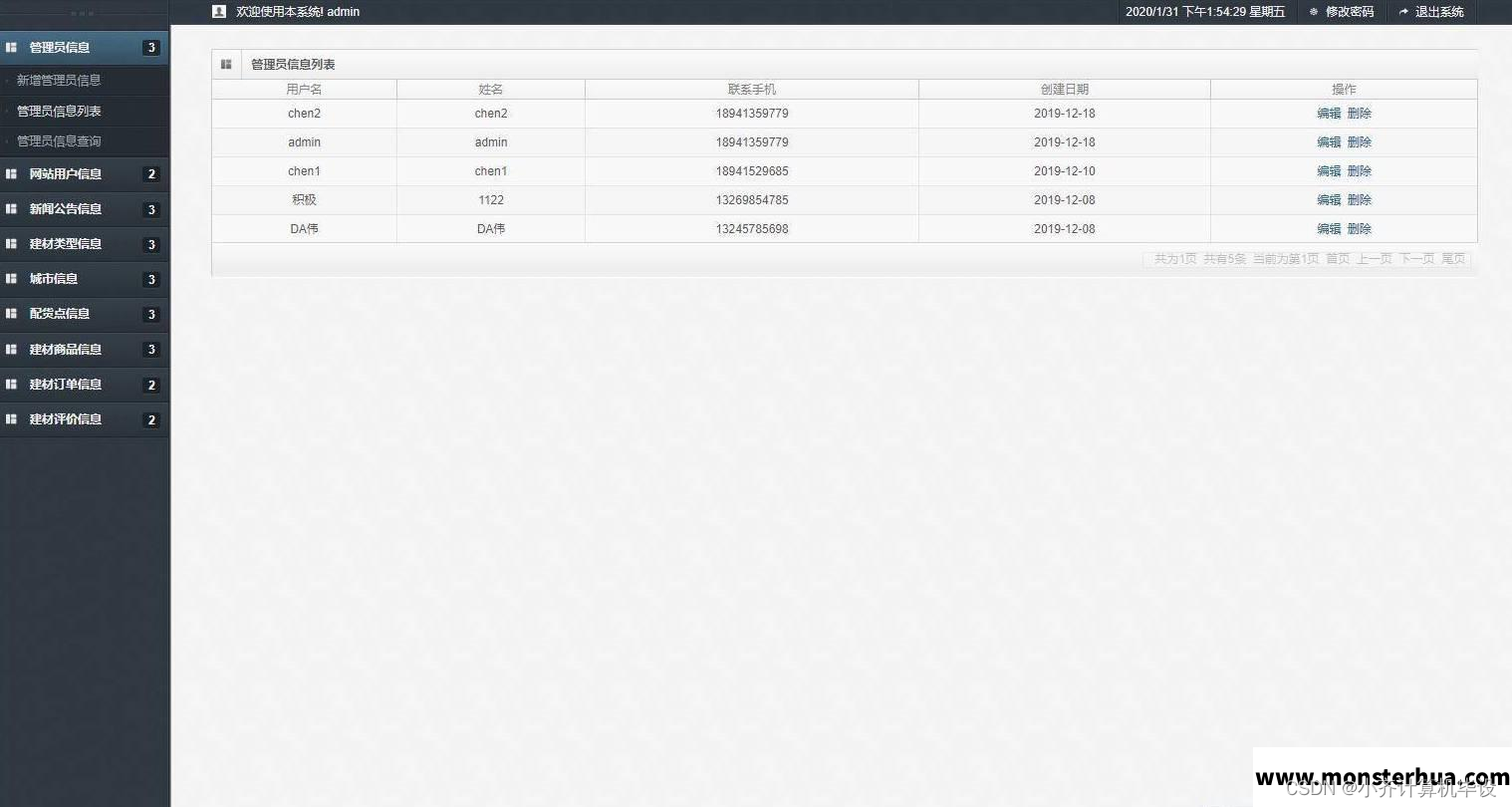
SSM建材商城网站----计算机毕业设计
项目介绍 本项目分为前后台,前台为普通用户登录,后台为管理员登录; 管理员角色包含以下功能: 管理员登录,管理员管理,注册用户管理,新闻公告管理,建材类型管理,配货点管理,建材商品管理,建材订单管理,建材评价管理等功能。 用…...

js逆向第9例:猿人学第2题-js混淆-动态cookie1
题目2:提取全部5页发布日热度的值,计算所有值的加和,并提交答案 (感谢蔡老板为本题提供混淆方案) 既然题目已经给出了cookie问题,那就从cookie入手,控制台找到数据请求地址 可以看到如下加密字符串m类似md5,后面跟着时间戳 m=45cc41dcdb15159ebb50564635f8e362|1704301…...
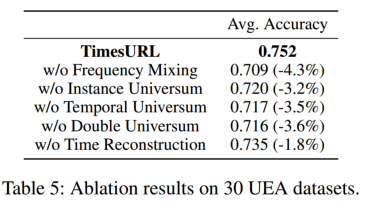
[论文分享]TimesURL:通用时间序列表示学习的自监督对比学习
论文题目:TimesURL: Self-supervised Contrastive Learning for Universal Time Series Representation Learning 论文地址:https://arxiv.org/abs/2312.15709 代码地址:暂无 摘要 学习适用于各种下游任务的通用时间序列表示具有挑战性&…...
解决sublime中文符号乱码问题
效果图 原来 后来 问题不是出自encode文件编码,而是win10的字体问题。 解决方法 配置: { "font_face":"Microsoft Yahei", "dpi_scale": 1.0 } 参考自 Sublime 输入中文显示方框问号乱码_sublime中文问号-CSDN博…...

厚积薄发11年,鸿蒙究竟有多可怕
12月20日中国工程院等权威单位发布《2023年全球十大工程成就》。本次发布的2023全球十大工程成就包括“鸿蒙操作系统”在内。入围的“全球十大工程成就”,主要指过去五年由世界各国工程科技工作者合作或单独完成且实践验证有效的,并且已经产生全球影响…...
 pyDAL查询操作)
pyDAL一个python的ORM(4) pyDAL查询操作
1 、简单查询 rows db(db.person.dept marketing).select(db.person.id, db.person.name, db.person.dept) rows db(db.person.dept marketing).select() rows db(db.person.dept marketing).select(db.person.ALL) rows db().select(db.person.ALL) / db(db.person).se…...

如何通过Python将各种数据写入到Excel工作表
在数据处理和报告生成等工作中,Excel表格是一种常见且广泛使用的工具。然而,手动将大量数据输入到Excel表格中既费时又容易出错。为了提高效率并减少错误,使用Python编程语言来自动化数据写入Excel表格是一个明智的选择。Python作为一种简单易…...
跟着cherno手搓游戏引擎【2】:日志系统spdlog和premake的使用
配置: 日志库文件github: GitHub - gabime/spdlog: Fast C logging library. 新建vendor文件夹 将下载好的spdlog放入 配置YOTOEngine的附加包含目录: 配置Sandbox的附加包含目录: 包装spdlog: 在YOTO文件夹下创建…...
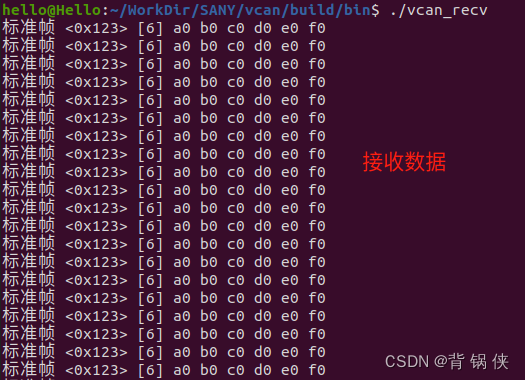
Ubuntu20.04 上启用 VCAN 用作本地调试
目录 一、启用本机的 VCAN 编辑 1.1 加载本机的 vcan 1.2 添加本机的 vcan0 1.3 查看添加的 vcan0 1.4 开启本机的 vcan0 1.5 关闭本机的 vcan0 1.6 删除本机的 vcan0 二、测试本机的 VCAN 2.1 CAN 发送数据 代码 2.2 CAN 接收数据 代码 2.3 CMakeLists.…...

LeetCode(31) 下一个排列
整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。 例如,arr [1,2,3] ,以下这些都可以视作 arr 的排列:[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。 整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地…...
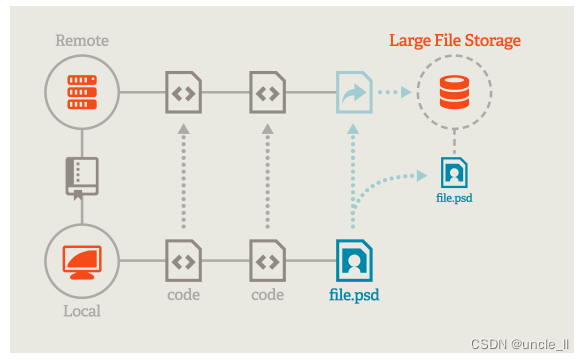
Git LFS: 简单高效的大文件版本控制
Git Large File Storage 问题 在使用git上传大文件时候,git push时候会报错: remote: error: File xxx.tar.gz is 135.17 MB; this exceeds GitHubs file size limit of 100 MB可以看到,git限制上传大小是100MB,超过的话就会报错ÿ…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...
