浅谈指数移动平均(ema)
经常在各种代码中看到指数移动平均(比如我专注的网络传输领域),但却不曾想到它就是诠释世界的方法,我们每个人都在被这种方式 “平均”…
今天说说指数移动平均(或移动指数平均,Exponential Moving Average)。
能查到的资料都侧重于其数学形式和实现,比如卷积和 python,这一点不再赘述,所以要写点内涵,物理意义和哲学。
指数移动平均在我们遇到的很多时间序采样中应用甚广,比如 tcp 的 srtt,它在形式上如下:
V n = ( 1 − β ) ∗ V n − 1 + β ∗ C V_n=(1-\beta)*V_{n-1}+\beta*C Vn=(1−β)∗Vn−1+β∗C
其中 C 为当前采样值,而 Vn 就是该采样序列的指数移动平均。
ema 的形式极端简洁,它只需要拿当前采用进行增量计算,不需要保存任何历史采样,其形式中,beta 为当下值权重,1 - beta 则留给过往,这非常符合我们的思维习惯。
我们认识的每一件事物,其本质都在采样,我们将当前采用叠加在对该采用的历史记忆之上,一杯敬当下,一杯敬过往,形成对世界的理解,形成我们的观点,我们的整个世界每时每刻对每件事物都在做指数移动平均。
将形式展开,我们将发现我们理解世界的过程:
V n = β ∗ C + ( 1 − β ) ∗ V n − 1 V_n=\beta*C+(1-\beta)*V_{n-1} Vn=β∗C+(1−β)∗Vn−1
V n = β ∗ C n + ( 1 − β ) ∗ ( β ∗ C n − 1 + ( 1 − β ) ∗ V n − 2 ) V_n=\beta*C_n+(1-\beta)*(\beta*C_{n-1}+(1-\beta)*V_{n-2}) Vn=β∗Cn+(1−β)∗(β∗Cn−1+(1−β)∗Vn−2)
…
V n = β ∗ ( 1 − β ) 0 ∗ C n + β ∗ ( 1 − β ) 1 ∗ C n − 1 + β ∗ ( 1 − β ) 2 ∗ C n − 2 + β ∗ ( 1 − β ) 3 ∗ C n − 3 + . . . β ∗ ( 1 − β ) n ∗ C 0 = Σ m = 0 n ( 1 − β ) m ∗ β C n − m V_n=\beta*(1-\beta)^0*C_n+\beta*(1-\beta)^1*C_{n-1}+\beta*(1-\beta)^2*C_{n-2}+\beta*(1-\beta)^3*C_{n-3}+...\beta*(1-\beta)^n*C_0=\Sigma_{m=0}^{n}{(1-\beta)^m*\beta C_{n-m}} Vn=β∗(1−β)0∗Cn+β∗(1−β)1∗Cn−1+β∗(1−β)2∗Cn−2+β∗(1−β)3∗Cn−3+...β∗(1−β)n∗C0=Σm=0n(1−β)m∗βCn−m
这里不讲卷积的形式,只从物理意义上理解 Vn 的每一项都是一个采样值 Cx 和一个 1 - beta 次幂的乘积的原因。下面开始。
假设我们的大脑能无差别均匀等价记忆所有采样值,我们的记忆是:
M = { C n , C n − 1 , C n − 2 , C n − 3 , . . . } M=\{C_{n},C_{n-1},C_{n-2},C_{n-3},...\} M={Cn,Cn−1,Cn−2,Cn−3,...}
然而我们不可能无差别记住所有采样,我们记忆容量有限,我们倾向于逐渐忘掉过往。由于历史记忆存在,当前采样仅能占据一部分记忆空间,这就是 β ∗ C \beta*C β∗C,那么 1 − β 1-\beta 1−β 的份额将留给过往,所有的过往将共享这 1 − β 1-\beta 1−β 的份额,这意味着随着新采样的不断进入,每一个历史采样必须衰减,历史越久的样本衰减越厉害,即 “逐渐忘掉过往” 。
M 集合按照历史时间序排序采样值 C,由于它进入记忆时均以 beta 份额压缩,事实上的 M 为:
M = { β ∗ C n , β ∗ C n − 1 , β ∗ C n − 2 , β ∗ C n − 3 , . . . } M=\{\beta*C_{n},\beta*C_{n-1},\beta*C_{n-2},\beta*C_{n-3},...\} M={β∗Cn,β∗Cn−1,β∗Cn−2,β∗Cn−3,...}
它的每一项被一个同样的按历史时间序加速衰减的集合过滤:
F = { ( 1 − β ) 0 , ( 1 − β ) 1 , ( 1 − β ) 2 , ( 1 − β ) 3 , . . . } F=\{(1-\beta)^0,(1-\beta)^1,(1-\beta)^2,(1-\beta)^3,...\} F={(1−β)0,(1−β)1,(1−β)2,(1−β)3,...}
把集合 M 往下漏被集合 F 阻隔过滤,就形成了新的集合 V:
V = { β ∗ C n ∗ ( 1 − β ) 0 , β ∗ C n − 1 ∗ ( 1 − β ) 1 , β ∗ C n − 2 ∗ ( 1 − β ) 2 , β ∗ C n − 3 ∗ ( 1 − β ) 3 , . . . } V=\{\beta*C_n*(1-\beta)^0,\beta*C_{n-1}*(1-\beta)^1,\beta*C_{n-2}*(1-\beta)^2,\beta*C_{n-3}*(1-\beta)^3,...\} V={β∗Cn∗(1−β)0,β∗Cn−1∗(1−β)1,β∗Cn−2∗(1−β)2,β∗Cn−3∗(1−β)3,...}
这就是指数移动平均的各项,看这相乘的形式当然可以把它理解成某种加权,但名称不重要。而它恰好可以被规整为一种简洁的递推式:
V n = ( 1 − β ) ∗ V n − 1 + β ∗ C V_n=(1-\beta)*V_{n-1}+\beta*C Vn=(1−β)∗Vn−1+β∗C
这就是历史记忆的运转方式。指数移动平均的本质在于一个样本的影响力以何种程度衰减到微不足道的地步,毕竟我们没人在乎自己 1 万年前的祖先是吃肉还是喝粥。
每个时代都认为自己的时代最特殊,最重要,但很快就被下个时代取而代之,淹没在历史长河。谁都逃不过指数移动被平均,过不了 100 年,人人乐道的改变世界的信息时代也将不过是一场平凡的技术革新罢了。
beta 如何选择取决于你想保存多久的记忆,或者说你容忍多久以前的采样可以忽略不计。
如果你希望的记忆周期为 100,在上述集合 V 中,数到第 100 个元素,它的衰减系数是集合 F 的第 100 项 (1 - beta)^99,只要它足够小,它后面的就相当于被彻底遗忘忽略不计了。
多小算足够小呢?取决于你自己。比如你认为 0.2 就足够小了,那就求解 (1 - beta)^99 > 0.2,选择一个 beta 即可。
前几天我论述的 dctcp,alpha 的系数 g 如何算呢:
α = ( 1 − g ) ∗ α + g ∗ F \alpha=(1-g)*\alpha+g*F α=(1−g)∗α+g∗F
一个 F 需要延展到整个拥塞周期,在该周期内它均需要表现出影响力,设一个拥塞周期为 T,选定一个足够小到不被在乎的数 Q,只要在满足 ( 1 − g ) T > Q (1-g)^T>Q (1−g)T>Q的 g 调得一手好参数即可。
如果既不知道什么是足够小,也不知道采样值的影响力周期,那就选择 1 / e 好了,因为 ( 1 − r ) 1 r (1-r)^{\frac{1}{r}} (1−r)r1 的极限就是 1 / e,此时就求 ( 1 − β ) 1 β = 1 e (1-\beta)^{\frac{1}{\beta}}=\dfrac{1}{e} (1−β)β1=e1 或 β 1 1 − β = 1 e \beta^{\frac{1}{1-\beta}}=\dfrac{1}{e} β1−β1=e1就好,取决于你偏好当前还是偏好过往。
浙江温州皮鞋湿,下雨进水不会胖。
相关文章:
)
浅谈指数移动平均(ema)
经常在各种代码中看到指数移动平均(比如我专注的网络传输领域),但却不曾想到它就是诠释世界的方法,我们每个人都在被这种方式 “平均”… 今天说说指数移动平均(或移动指数平均,Exponential Moving Average)。 能查到的资料都侧重于其数学形…...

1-并发编程线程基础
什么是线程 在讨论什么是线程前有必要先说下什么是进程,因为线程是进程中的一个实体,线程本身是不会独立存在的。 进程是代码在数据集合上的一次运行活动,是系统进行资源分配和调度的基本单位,线程则是进程的一个执行路径&#…...
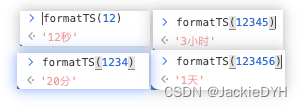
vue中动态出来返回的时间秒数,在多少范围显示多少秒,多少范围显示分,小时等等
在Vue中,你可以使用计算属性(computed property)或过滤器(filter)来根据动态返回的时间秒数来显示不同的时间单位,比如秒、分、小时等等。 下面是一个使用计算属性的示例: <template>&l…...

English: go through customs
文章目录 常见单词机场指示登机和中转降落以及公共服务签证篇出/入境卡篇入境英语会话篇 常见单词 customs: 海关 (kʌstəmz)cash: 现金 (kʃ)passport: 护照 (pspɔːt)luggage/baggage: 行李 (lʌɡɪdʒ/ˈbɡɪdʒ)Exchange: 换钱 (ɪks’tʃeɪndʒ)airport: 飞机场 (ɛ…...
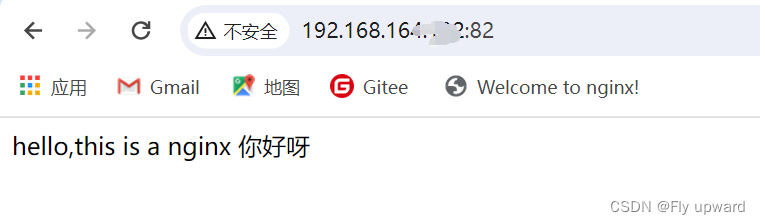
Nginx 多端口部署多站点
目录 1.进行nginx.conf 2.复制粘贴 3.修改端口及站点根目录 4. 网站上传 1.进行nginx.conf 在 nginx 主要配置文件 nginx.conf 中,server 是负责一个网站配置的,我们想要多个端口访问的话,可以复制多个 server 先进入到 nginx.conf 中 …...
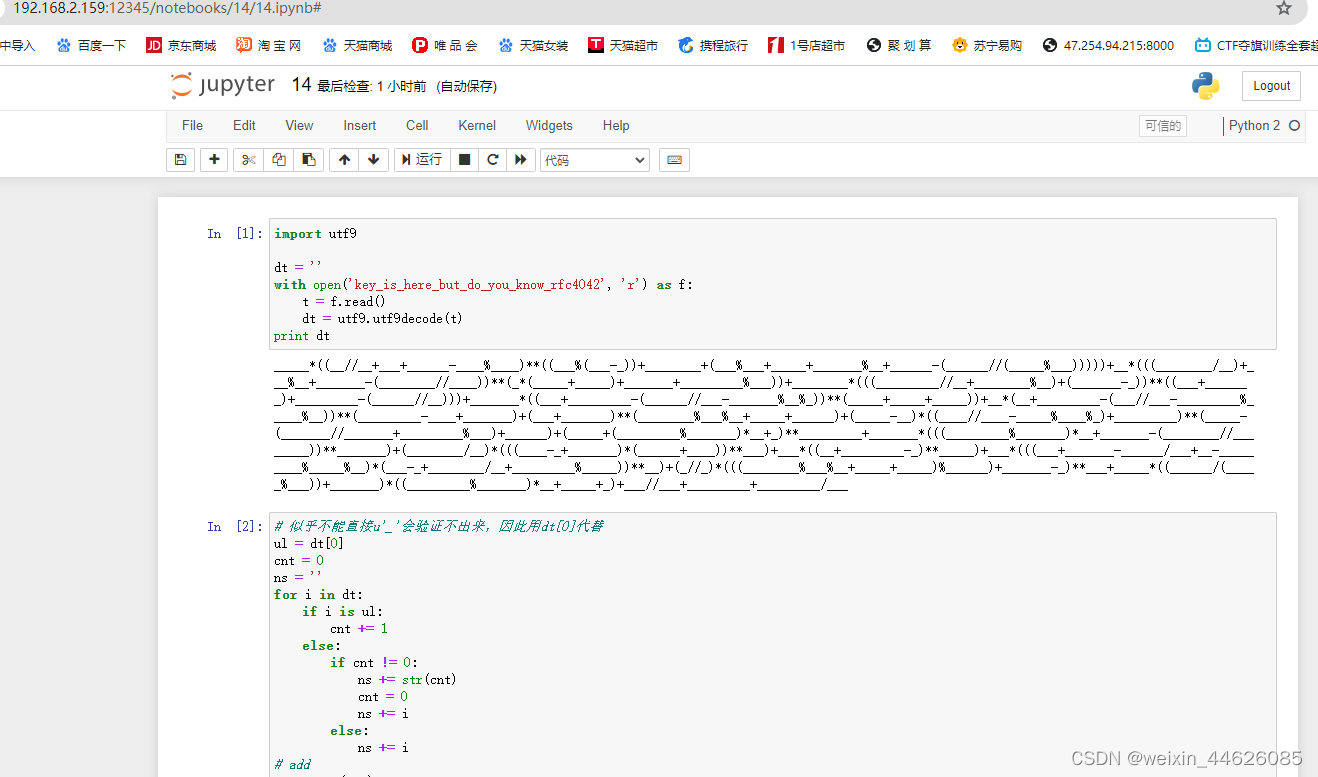
从零开始配置kali2023环境:配置jupyter的多内核环境
在kali2023上面尝试用anaconda3,anaconda2安装实现配置jupyter的多内核环境时出现各种问题,现在可以通过镜像方式解决 1. 搜索镜像 ┌──(holyeyes㉿kali2023)-[~] └─$ sudo docker search anaconda ┌──(holyeyes㉿kali2023)-[~] └─$ sudo …...

Dart调用JS对10000条定位数据滤波
使用Dart调用JS,还是为了练习跨语言调用; 一、编写对应的JS代码 平时在开发时不推荐将算法放在JS里,我这里是简单的做一下数据过滤; 首先生成一些随机定位数据,在实际开发中可以使用真实数据; // 随机定…...

大模型应用实践:AIGC探索之旅
随着OpenAI推出ChatGPT,AIGC迎来了前所未有的发展机遇。大模型技术已经不仅仅是技术趋势,而是深刻地塑造着我们交流、工作和思考的方式。 本文介绍了笔者理解的大模型和AIGC的密切联系,从历史沿革到实际应用案例,再到面临的技术挑…...

【.NET Core】异步编程模式
【.NET Core】异步编程模式 文章目录 【.NET Core】异步编程模式一、概述二、基于任务的异步模式(TAP)2.1 TAP模式命名、参数和返回类型2.2 TAP初始化异步操2.3 TAP如何编译2.4 手动生成TAP方法2.5 混合方法实现TAP2.6 TAP中Await挂起执行2.7 TAP中使用Y…...

macOS通过外置驱动器备份数据
通过外置驱动器备份数据(谨慎操作) 1.将外置驱动器连接到您的 Mac。驱动器容量应等于或大于您当前的启动磁盘。驱动器还应该是您可以抹掉的。 2.使用 macOS 恢复功能 抹掉外置驱动器,然后将 macOS 安装 到外置驱动器上。确保您选择的外置驱动…...
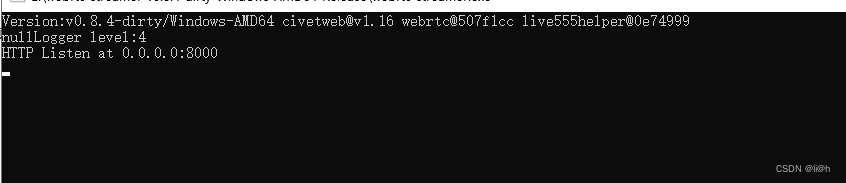
rtsp解析视频流
这里先说一下 播放rtsp 视频流,尽量让后端转换一下其他格式的流进行播放。因为rtsp的流需要flash支持,现在很多浏览器不支持flash。 先说一下这里我没有用video-player插件,因为它需要用flash ,在一个是我下载flash后,还是无法播放…...

【物联网】手把手完整实现STM32+ESP8266+MQTT+阿里云+APP应用——第3节-云产品流转配置
🌟博主领域:嵌入式领域&人工智能&软件开发 本节目标:本节目标是进行云产品流转配置为后面实际的手机APP的接入做铺垫。云产品流转配置的目的是为了后面能够让后面实际做出来的手机APP可以控制STM32/MCU,STM32/MCU可以将数…...
)
Spring Cloud Config相关问题及答案(2024)
1、什么是 Spring Cloud Config,它解决了哪些问题? Spring Cloud Config 是一个为微服务架构提供集中化外部配置支持的项目。它是构建在 Spring Cloud 生态系统之上,利用 Spring Boot 的开发便利性,简化了分布式系统中的配置管理…...
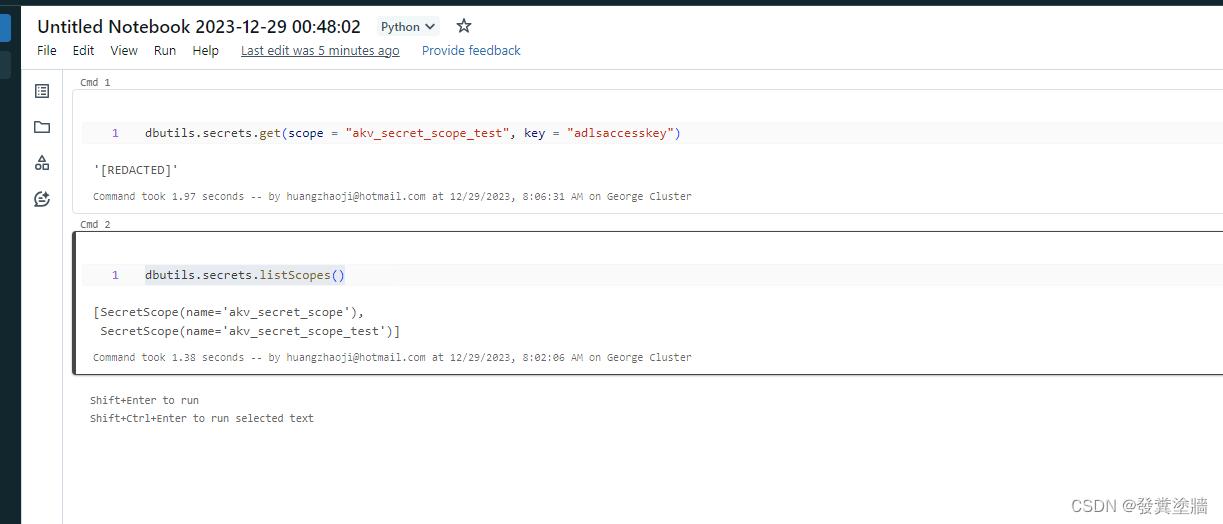
【Azure 架构师学习笔记】- Azure Databricks (4) - 使用Azure Key Vault 管理ADB Secret
本文属于【Azure 架构师学习笔记】系列。 本文属于【Azure Databricks】系列。 接上文 【Azure 架构师学习笔记】- Azure Databricks (3) - 再次认识DataBricks 前言 Azure Databricks有access token,是具有ADB内部最高权限的token。在云环境中这些高级别权限的sec…...

[每周一更]-(第50期):Go的垃圾回收GC
参考文章: https://juejin.cn/post/7111515970669117447https://draveness.me/golang/docs/part3-runtime/ch07-memory/golang-garbage-collector/https://colobu.com/2022/07/16/A-Guide-to-the-Go-Garbage-Collector/https://liangyaopei.github.io/2021/01/02/g…...
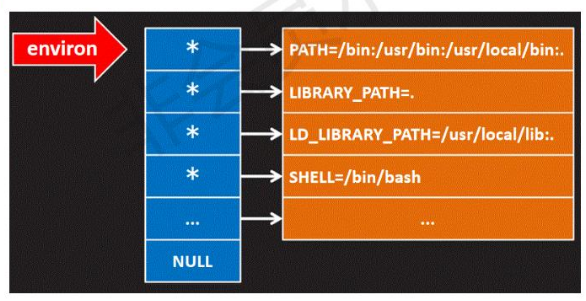
【嵌入式学习笔记-01】什么是UC,操作系统历史介绍,计算机系统分层,环境变量(PATH),错误
【嵌入式学习笔记】什么是UC,操作系统历史介绍,计算机系统分层,环境变量(PATH),错误 文章目录 什么是UC?计算机系统分层什么是操作系统? 环境变量什么是环境变量?环境变量的添加&am…...

【动态规划】LeetCode-10. 正则表达式匹配
10. 正则表达式匹配。 给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 ‘.’ 和 ‘*’ 的正则表达式匹配。 ‘.’ 匹配任意单个字符‘*’ 匹配零个或多个前面的那一个元素 所谓匹配,是要涵盖 整个 字符串 s的,而不是部分字符串。 …...

lenovo联想拯救者8.8英寸掌上游戏机Legion Go 8APU1(83E1)原装出厂Windows11预装系统
链接:https://pan.baidu.com/s/1d586XWXcAWVxlLyV2Oku7Q?pwdd74t 提取码:d74t 系统自带所有驱动、出厂主题壁纸、Office办公软件、联想电脑管家等预装程序 所需要工具:16G或以上的U盘 文件格式:ISO 文件大小:…...
复现YOLOV1(4)VOC2007数据集的读取及预处理)
经典目标检测YOLO系列(一)复现YOLOV1(4)VOC2007数据集的读取及预处理
经典目标检测YOLO系列(一)复现YOLOV1(4)VOC2007数据集的读取及预处理 之前,我们依据《YOLO目标检测》(ISBN:9787115627094)一书,提出了新的YOLOV1架构,并解决前向推理过程中的两个问题,继续按照此书进行YOLOV1的复现。 经典目标检…...
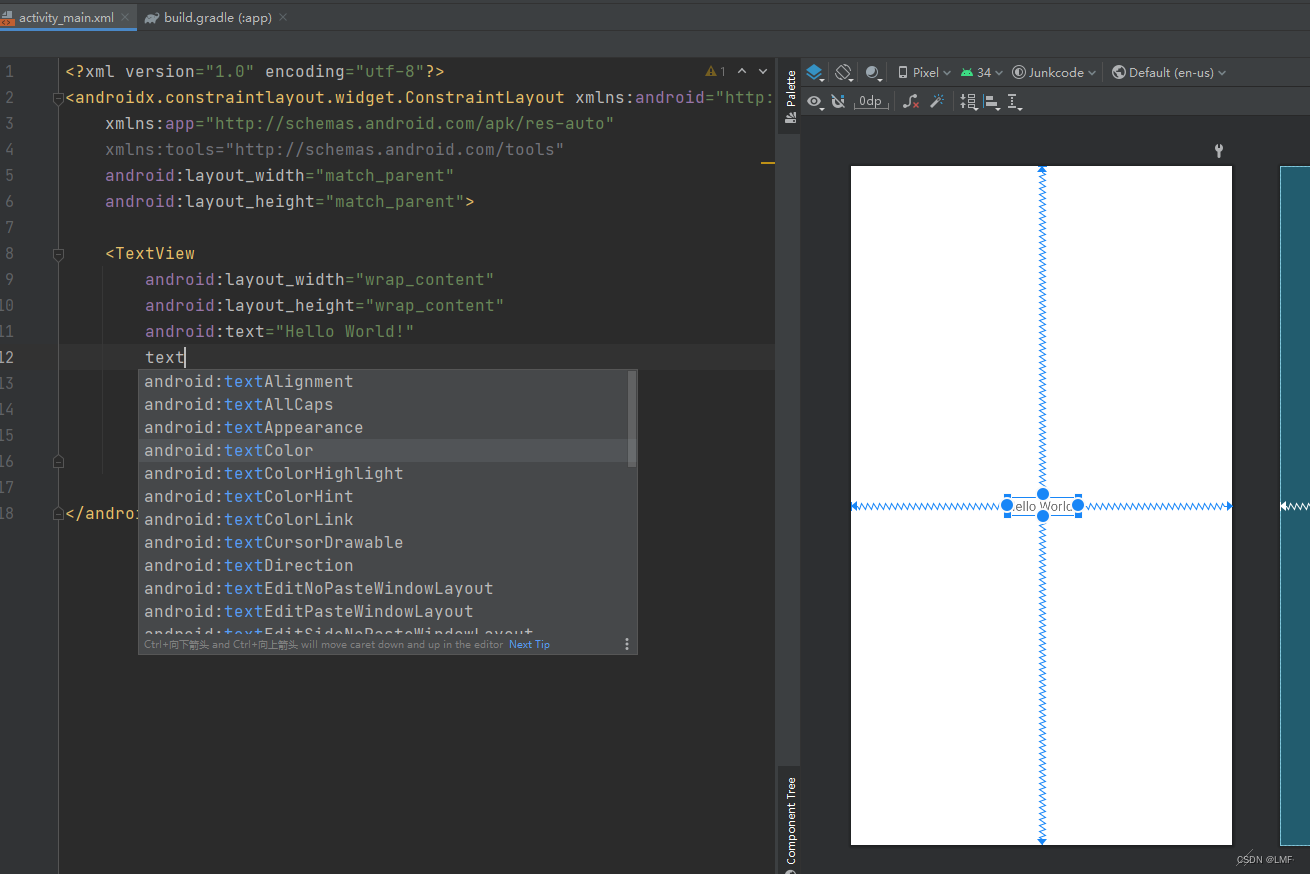
Android Studio xml布局代码补全功能失效问题
这里写目录标题 前言:问题描述原因分析:解决方案:1.更新 Android Studio 版本2.原版本解决XML补全失效 小结 前言: 在开发过程中,你可能遇到很多奇奇怪怪的问题。Android Studio 编译器出现问题也是常有的事情&#x…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...
