国科大图像处理2024速通期末——汇总2017-2019、2023回忆
国科大2023.12.28图像处理0854期末重点
图像处理 王伟强 作业 课件 资料
一、填空
- 一个阴极射线管它的输入与输出满足 s = r 2 s=r^{2} s=r2,这将使得显示系统产生比希望的效果更暗的图像,此时伽马校正通常在信号进入显示器前被进行预处理,令p与q表示伽马校正的输入与输出,则p与q之间的映射关系式表示为: q = p 1 2 q=p^{\frac{1}{2}} q=p21
- 卷积是一种图像处理领域最有影响力的计算之一,对于一幅输入图像f(x,y), 我们可以通过卷积运算产生一幅新的图像g(x,y),若g(x,y)=0.1f(x+1,y)+0.2f(x-1y)+0.3f(x,y)+0.2f(x,y-1)+0.2f(x,y+1)这里x表示行标,y表示图像中像素位置的列坐标,请用一个3X3的矩阵来表示这个卷积核
- 我们处理一幅图像可以在空域中通过线性滤波运算进行处理,也可以在频域内对它进行处理达到同样的效果。该事实的理论基础就是基于傅立叶变换的卷积定理,若我们用f(x,y),g(x,y)表示图像与线性滤波核,它们对应的傅立叶变换分别用F(u,v),G(u,v)表示则该定理可形式化描述为f(x,y)∗g(x,y)⟷F(u,v)×G(u,v)(2023秋)
- 拉普拉斯波器的频域表示的函数形式为 H ( u , v ) = − 4 π 2 ( u 2 + v 2 ) H(u,v)=-4\pi ^{2}(u^{2}+v^{2}) H(u,v)=−4π2(u2+v2)
- 假设我们有一个在0-1区间的均匀分布随机数发生器w,若已知一个满足瑞利分布的随机变量累加分布函数CDF是 F z ( z ) = { 1 − e x p ( − ( z − a ) 2 b ) , z ≥ a 0 , z < a F_{z}(z)=\begin{cases} 1-\frac{exp(-(z-a)^{2}}{b}),z\ge a\\ 0,z<a \end{cases} Fz(z)={1−bexp(−(z−a)2),z≥a0,z<a,则基于w的瑞利分布的随机数发生器z的方程为 z = a + − b l n ( 1 − w ) z=a+\sqrt{-bln(1-w)} z=a+−bln(1−w)
- 若高斯低通滤波器在频域中的表示为 H ( u , v ) = e − D 2 ( u , v ) 2 D 0 2 H(u,v)=e^{-\frac{D^{2}(u,v)}{2D_{0}^{2}}} H(u,v)=e−2D02D2(u,v)则对应的高斯高通滤波器在频域中的表示为 H h ( u , v ) = 1 − e − D 2 ( u , v ) 2 D 0 2 H_{h}(u,v)=1-e^{-\frac{D^{2}(u,v)}{2D_{0}^{2}}} Hh(u,v)=1−e−2D02D2(u,v)
- Weiner 滤波的计算方法为 F ( u , v ) = [ 1 H ( u , v ) ⋅ ∣ H ( u , v ) ∣ 2 ∣ H ( u , v ) ∣ 2 + S η ( x , y ) S f ( x , y ) ] G ( u , v ) ) F(u,v)=[\frac{1}{H(u,v)}·\frac{|H(u,v)|^{2}}{|H(u,v)|^{2}+\frac{S_{\eta }(x,y)}{S_{f}(x,y)}}]G(u,v)) F(u,v)=[H(u,v)1⋅∣H(u,v)∣2+Sf(x,y)Sη(x,y)∣H(u,v)∣2]G(u,v))其中 S η ( x , y ) S_{\eta }(x,y) Sη(x,y)代表噪声功率谱密度,H(u,v)代表退化函数(2023秋)
- YCbCr中的Y代表明度,Cb与Cr代表蓝色与红色的浓度偏移,HSV中的H代表色调,s代表饱和度(2023秋)
二、选择
-
采用对比度拉伸是实现灰度图像的增强的一种重要思路,而分段线性变换函数是一种常被采用的技术。针对某一段输入灰度范围,若你想扩大输出灰度的动态范围,所构造的那一段线性映射函数的斜率k应满足:(A)(2023秋)
A.k>1
B.k=1
C.k<1
D.取任何值都可以 -
若一幅图像中存在椒盐噪声,下面哪种滤波器可选择来去除它们:(D)
A.算术均值滤波器
B.反调和滤波器
C.拉普拉斯滤波器
D.中值滤波器 -
通过卷积运算对图像进行各种目的的滤波是图像处理的重要内容。对于离散的两个一维信号[3,5,6],g=[1,-1],对应的卷积结果是(A)(2023秋)
A.[3,2,1,-6]
B.[2.1]
C.[-3,-2-1,6]
D.[-2,-1] -
高斯低通滤波器 H ( u , v ) = e − D 2 ( u , v ) 2 D 0 2 H(u,v)=e^{-\frac{D^{2}(u,v)}{2D_{0}^{2}}} H(u,v)=e−2D02D2(u,v)中存在一个参数 D 0 D_{0} D0,对于一幅中年妇女面部特写图像,若发现采用 D 0 = 100 D_{0}=100 D0=100时,去除该妇女眼部的皱纹不彻底,则应该:(A)
A.适当减小 D 0 D_{0} D0
B.适当加大 D 0 D_{0} D0
C.保持 D 0 D_{0} D0不变
D.前面选项都不对 -
对于一个具有正交性质的完美重建滤波器组,若它的滤波器之间具有如下的关系:(B)
g 1 ( n ) = ( − 1 ) n g 0 ( 2 K − 1 − n ) , h 1 ( n ) = g 1 ( 2 K − 1 − n ) , i = 0 , 1 g_{1}(n)=(-1)^{n}g_{0}(2K-1-n),h_{1}(n)=g_{1}(2K-1-n),i=0,1 g1(n)=(−1)ng0(2K−1−n),h1(n)=g1(2K−1−n),i=0,1A. ( − 1 ) n h 0 ( 2 K − 1 − n ) (-1)^{n}h_{0}(2K-1-n) (−1)nh0(2K−1−n)
B. ( − 1 ) n + 1 h 0 ( 2 K − 1 − n ) (-1)^{n+1}h_{0}(2K-1-n) (−1)n+1h0(2K−1−n)
C. ( − 1 ) n h 0 ( n ) (-1)^{n}h_{0}(n) (−1)nh0(n)
D. ( − 1 ) n + 1 h 0 ( n ) (-1)^{n+1}h_{0}(n) (−1)n+1h0(n) -
信息论是信息压缩的理论基础,而互信息是信息论中一个非常重要的概念,信源z与信道输出v之间互信息I(z,v)的意义为©
A.信源z与信道输出v间的平均信息量
B.观察单一信道输出符号时接收到的平均信息
C.观测到输出v后信源符号的平均信息量
D信道可靠传输信息的最大传送率
三、判断
- 对一幅数字图像进行一次直方图均衡处理后,通常不会产生非常绝对平的直方图。即便我们对处理后的图像再进行一次直方图处理,理论上也不会产生任何效果。(√)
- 拉普拉斯滤波器与统计排序滤波器均不是一种卷积运算。(×)
- 卷积运算具有交换性与结合性。(√)
- 低通高阶巴特沃斯滤波器存在振铃效应,而低通高斯滤波器不存在振铃效应。(√)
- 我们可以用阶数Q<0的逆谐波均值滤波器来去除盐噪声。(√)
- 给定一幅图像,若我们能准确估计噪声的均值与方差,则可以知道噪声的能量(所有像素位置的噪声强度的平方和)。(√)
- 在图像编码中,涉及信源编码与信道编码,两者都是为了实现信息的压缩表示。(×)
- 对于一个事件,它发生的概率越小,它的熵越大。(×)(2023秋)
- 若一幅图像中含有一些噪声点或干扰性微小结构,可采用形态处理中的开操作作为一种处理段来去除它。(√)
四、简答
1. 简述什么是线性移不变系统(2023秋)
答:线性移不变性系统(Linear Shift-Invariant System,简称LSI系统)是一种特殊的系统,它对输入图像的处理满足线性和移不变性两个条件。
- 线性:系统对输入图像的处理是线性的,即如果输入图像是两个图像的线性组合,那么输出图像也是这两个图像经过系统处理后的输出的相同线性组合。数学上表示为,如果 f 1 ( x , y ) f_{1}(x,y) f1(x,y)和 f 2 ( x , y ) f_{2}(x,y) f2(x,y)是两个输入图像,α和β是任意常数,那么系统的输出满足: S ( α f 1 + β f 2 ) = α S ( f 1 ) + β S ( f 2 ) S(αf_{1}+βf_{2})=αS(f_{1})+βS(f_{2}) S(αf1+βf2)=αS(f1)+βS(f2)
- 移不变性:系统对输入图像的处理是移不变的,即如果输入图像在空间域内平移,那么输出图像也会相应地平移,而不会改变其它特性。数学上表示为,如果f(x,y)是输入图像, ( x 0 , y 0 ) (x_{0},y_{0}) (x0,y0)是平移量,那么系统的输出满足: H [ f ( x , y ) ] = g ( x , y ) , H [ f ( x − x 0 , y − y 0 ) ] = g ( x − x 0 , y − y 0 ) H[f(x,y)]=g(x,y),H[f(x-x_{0},y-y_{0})]=g(x-x_{0},y-y_{0}) H[f(x,y)]=g(x,y),H[f(x−x0,y−y0)]=g(x−x0,y−y0)
线性移不变性系统的一个重要特性是,它们可以通过卷积运算来描述。对于任何LSI系统,都存在一个称为系统冲激响应的函数 h ( x , y ) h(x,y) h(x,y),使得系统对任何输入图像 f ( x , y ) f(x,y) f(x,y) 的输出 g ( x , y ) g(x,y) g(x,y)可以表示为 f ( x , y ) f(x,y) f(x,y)和 h ( x , y ) h(x,y) h(x,y)的卷积: g ( x , y ) = f ( x , y ) ∗ h ( x , y ) g(x,y)=f(x,y)\ast h(x,y) g(x,y)=f(x,y)∗h(x,y)
2. 观察如下所示图像。右边的图像这样得到:
(a)在原始图像左边乘以 ( − 1 ) x + y (-1)^{x+y} (−1)x+y;
(b) 计算离散傅里叶变换(DFT);
© 对变换取复共轭;
(d) 计算傅里叶反变换;
(e) 结果的实部再乘以 ( − 1 ) x + y (-1)^{x+y} (−1)x+y。
(用数学方法解释为什么会产生右图的效果)。DIP旋转了180度
假设原图像为 f 1 ( x , y ) f_{1}(x,y) f1(x,y)
- 经过a操作变为 ( − 1 ) x + y f 1 ( x , y ) (-1)^{x+y}f_{1}(x,y) (−1)x+yf1(x,y)
- 经过b操作离散傅里叶变换变为 F ( u , v ) = 1 M N ∑ u = 0 M − 1 ∑ v = 0 N − 1 ( − 1 ) x + y f ( x , y ) e − j 2 π ( u x M + u y N ) F(u,v)=\frac{1}{MN}\sum_{u=0}^{M-1}\sum_{v=0}^{N-1}{(-1)^{x+y}f(x,y)e^{-j2\pi\left(\frac{ux}{M}+\frac{uy}{N}\right)}} F(u,v)=MN1∑u=0M−1∑v=0N−1(−1)x+yf(x,y)e−j2π(Mux+Nuy)
- 通过c操作,根据傅里叶变换性值
- F ∗ ( u , v ) = 1 M N ∑ u = 0 M − 1 ∑ v = 0 N − 1 ( − 1 ) x + y f ( x , y ) e j 2 π ( u x M + u y N ) F^\ast (u,v)=\frac{1}{MN}\sum_{u=0}^{M-1}\sum_{v=0}^{N-1}{(-1)^{x+y}f(x,y)e^{j2\pi\left(\frac{ux}{M}+\frac{uy}{N}\right)}} F∗(u,v)=MN1∑u=0M−1∑v=0N−1(−1)x+yf(x,y)ej2π(Mux+Nuy)
- 通过d操作得傅里叶反变换变为
- I D F T ( F ∗ ( u , v ) ) = 1 M N ∑ u = 0 M − 1 ∑ v = 0 N − 1 [ 1 M N ∑ u = 0 M − 1 ∑ v = 0 N − 1 ( − 1 ) x + y f ( x , y ) e j 2 π ( u x M + u y N ) ] e j 2 π ( u x M + u y N ) IDFT(F^\ast (u,v))=\frac{1}{MN}\sum_{u=0}^{M-1}\sum_{v=0}^{N-1}[\frac{1}{MN}\sum_{u=0}^{M-1}\sum_{v=0}^{N-1}{(-1)^{x+y}f(x,y)e^{j2\pi\left(\frac{ux}{M}+\frac{uy}{N}\right)}}]e^{j2\pi\left(\frac{ux}{M}+\frac{uy}{N}\right)} IDFT(F∗(u,v))=MN1∑u=0M−1∑v=0N−1[MN1∑u=0M−1∑v=0N−1(−1)x+yf(x,y)ej2π(Mux+Nuy)]ej2π(Mux+Nuy)实部为 ( − 1 ) x + y f ( − x , − y ) (-1)^{x+y}f(-x,-y) (−1)x+yf(−x,−y)
- e操作后变为 ( − 1 ) x + y ( − 1 ) x + y f ( − x , − y ) = f ( − x , − y ) (-1)^{x+y}(-1)^{x+y}f(-x,-y)=f(-x,-y) (−1)x+y(−1)x+yf(−x,−y)=f(−x,−y)
效果原图像旋转180°
3. 描述如何构建高斯金字塔与拉普拉斯金字塔(2023秋)
-
高斯金字塔建立:
- 生成初始图像(最底层): 将原始图像 f ( x , y ) f(x,y) f(x,y)作为金字塔的第一层。
- 进行下采样: 对当前层的图像进行高斯滤波,然后进行下采样,即去除一些行和列,以生成下一层的图像。下采样可以使用像素平均值或其他插值技术。下采样的目的是减小图像的尺寸。
- 重复步骤2: 重复进行高斯滤波和下采样,直到达到金字塔的顶层。每一层的图像尺寸都比前一层的尺寸小。
-
拉普拉斯金字塔建立:
- 生成高斯金字塔: 使用上述方法生成高斯金字塔。
- 构建拉普拉斯金字塔: 拉普拉斯金字塔的每一层都是由对应的高斯金字塔层与该层的上一层进行差分得到的。即,拉普拉斯金字塔的每一层是由高斯金字塔的对应层减去该层的上一层。对于每一层i,拉普拉斯金字塔的图像 L i L_{i} Li可以用以下公式表示: L i = G i − e x p a n e d ( G i + 1 ) L_{i}=G_{i}-expaned(G_{i+1}) Li=Gi−expaned(Gi+1)
其中, G i G_{i} Gi是高斯金字塔的第 i 层,expaned是上采样操作。这样,我们得到的拉普拉斯金字塔的第一层是高斯金字塔的最顶层,最后一层是高斯金字塔的最底层
4. 每一个小波的尺度函数都遵循Mallat提出的多分辨率分析的4个基本要求,请描述这4个基本要求的内容(2023秋)
答:
- 尺度函数对它的整数平移对应的函数是正交的
- 哈尔函数被称为是紧支撑的,意味着除了称为支撑域有限区间外,函数值都为0
- 必须注意,当尺度函数的支撑域大于1时,整数平移函数间的正交性将变得更加难于被满足 - 低尺度尺度函数张成的子空间包含于高尺度尺度函数张成的子空间内
V − ∞ ⊂ . . . ⊂ V − 1 ⊂ V − 0 ⊂ V 1 ⊂ . . . ⊂ V + ∞ V_{-∞} \subset ... \subset V_{-1}\subset V_{-0}\subset V_{1}\subset ...\subset V_{+∞} V−∞⊂...⊂V−1⊂V−0⊂V1⊂...⊂V+∞ - 唯一包含在 V j V_{j} Vj所有中的函数是f(x)=0
V − ∞ = 0 V_{-∞}=0 V−∞=0 - 任何函数都可以以任意精度表示 V ∞ = L 2 ( R ) V_{∞}=L^{2}(R) V∞=L2(R)
5. 傅里叶变换的6个性质
- 空域频移性 F [ f ( x − x 0 , y − y 0 ) ] = F ( u , v ) e − j 2 π ( u x 0 M + v y 0 N ) \mathscr{F}[f(x-x_{0},y-y_{0})]=F(u,v)e^{-j2\pi (\frac{ux_{0}}{M}+\frac{vy_{0}}{N})} F[f(x−x0,y−y0)]=F(u,v)e−j2π(Mux0+Nvy0)
- 时域频移性 F [ f ( x , y ) e − j 2 π ( u x 0 M + v y 0 N ) ] = F ( u − u 0 , v − v 0 ) \mathscr{F}[f(x,y)e^{-j2\pi (\frac{ux_{0}}{M}+\frac{vy_{0}}{N})}]=F(u-u_{0},v-v_{0}) F[f(x,y)e−j2π(Mux0+Nvy0)]=F(u−u0,v−v0)
- F [ f ( x , y ) ( − 1 ) x + y ] = F ( u − M 2 , v − N 2 ) \mathscr{F}[f(x,y)(-1)^{x+y}]=F(u-\frac{M}{2},v-\frac{N}{2}) F[f(x,y)(−1)x+y]=F(u−2M,v−2N) - 平均和对称
- 平均 F ( 0 , 0 ) = 1 M N ∑ u = 0 M − 1 ∑ v = 0 N − 1 f ( x , y ) F(0,0)=\frac{1}{MN}\sum_{u=0}^{M-1}\sum_{v=0}^{N-1}{f(x,y)} F(0,0)=MN1∑u=0M−1∑v=0N−1f(x,y)
- 共轭 F ( u , v ) = F ∗ ( − u , − v ) F(u,v)=F^{\ast}(-u,-v) F(u,v)=F∗(−u,−v)
- 对称 ∣ F ( u , v ) ∣ = ∣ F ( − u , − v ) ∣ |F(u,v)|=|F(-u,-v)| ∣F(u,v)∣=∣F(−u,−v)∣
- 可分离性 F ( u , v ) = F f ( x , y ) = ∑ y [ ∑ x f ( x , y ) e − j 2 π x u M ] e − j 2 π y v N = ∑ y F ( u , y ) e − j 2 π y v N F(u,v)=\mathscr{F}f(x,y)=\sum_{y}[\sum_{x}{f(x,y)e^{-j2\pi \frac{xu}{M}}}]e^{-j2\pi \frac{yv}{N}}=\sum_{y}F(u,y)e^{-j2\pi \frac{yv}{N}} F(u,v)=Ff(x,y)=∑y[∑xf(x,y)e−j2πMxu]e−j2πNyv=∑yF(u,y)e−j2πNyv
- 旋转性 x = r c o s θ , y = r s i n θ , u = ω c o s φ , v = ω s i n φ x=rcosθ ,y=rsinθ , u=\omega cos\varphi , v=\omega sin\varphi x=rcosθ,y=rsinθ,u=ωcosφ,v=ωsinφ
f ( r , θ + θ 0 ) ⇔ F ( ω , φ + θ 0 ) f(r,θ+θ_{0})\Leftrightarrow F(\omega,\varphi+θ_{0}) f(r,θ+θ0)⇔F(ω,φ+θ0) - 周期性f(x,y)=f(x+M,y)=f(x,y+N)=f(x+M,y+N)
F(u,v)=F(u+M,v)=F(u,v+N)=F(u+M,v+N) - 线性 F ( a f ( x , y ) + b g ( x , y ) ) = a F ( f ( x , y ) ) + b F ( g ( x , y ) ) \mathscr{F} (af(x,y)+bg(x,y))=a\mathscr{F} (f(x,y))+b\mathscr{F}(g(x,y)) F(af(x,y)+bg(x,y))=aF(f(x,y))+bF(g(x,y))
- 微分性
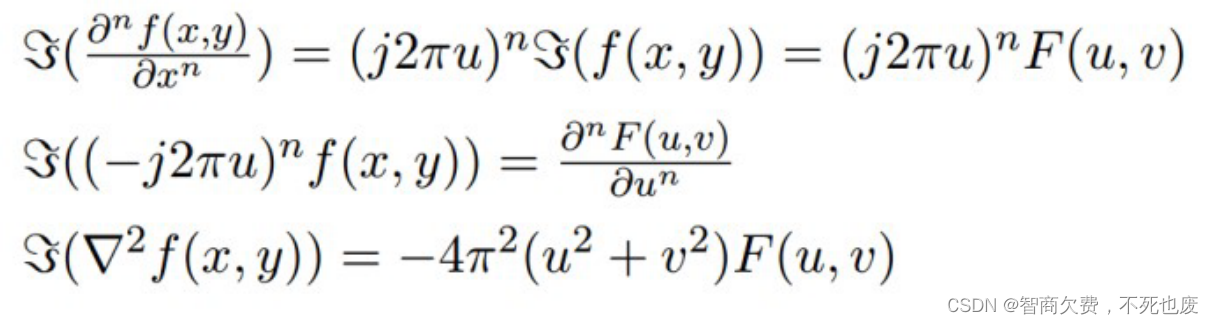
6. 请用集合的语言描述形态学中的腐蚀与膨胀,并用进一步用数学公式定义开运算与闭运算。
假设 A 是一个图像集合,并且 B 是一个称为结构元素的集合。
-
腐蚀(Erosion):
腐蚀操作可以看作是将结构元素 B 从图像 A 中滑动,只要 B 完全覆盖A 的某一部分,那么该部分就被保留,否则就被去除。
数学表述为: A ⊖ B = { z ∣ ( B ) z ⊆ A } A⊖B=\left \{ z∣(B)_{z}\subseteq A \right \} A⊖B={z∣(B)z⊆A}
⊖ 表示腐蚀操作, ( B ) z (B)_{z} (B)z表示将结构元素 B 的原点放在 z 处。 -
膨胀(Dilation):
膨胀操作可以看作是将结构元素 B 从图像 A 中滑动,只要B 与 A 有交集,那么该部分就被保留。
数学表述为: A ⊕ B = { z ∣ ( B ) z ⊆ A } A⊕B=\left \{ z∣(B)_{z}\subseteq A \right \} A⊕B={z∣(B)z⊆A}⊕ 表示膨胀操作 -
开运算(Opening):
开运算首先对图像进行腐蚀,然后再进行膨胀。这通常用于消除小的对象或噪声。
数学表述为: A ∘ B = ( A ⊕ B ) ⊖ B A∘B=(A⊕B)⊖B A∘B=(A⊕B)⊖B -
闭运算(Closing):
闭运算首先对图像进行膨胀,然后再进行腐蚀。这通常用于填充小的孔洞或连接不连续的对象。
数学表述为: A ⋅ B = ( A ⊖ B ) ⊕ B A·B=(A⊖B)⊕B A⋅B=(A⊖B)⊕B
7. 简述拉普拉斯算子、拉普拉斯算子的傅里叶变换表达式(2023秋)
8. 熵、条件熵、互信息的数学定义和物理意义。
五、计算
1.直方图均衡(2023秋)
一幅具有8个灰度级的图像的归一化直方图为[0.17 0.25 0.21 0.16 0.07 0.08 0.04 0.02],求直方图均衡后的灰度级和对应概率,并画出均衡后归一化直方图的示意图。
2. Z 变换证明
Z变换是一种信号分析的重要工具。它有许多重要的性质,请对如下性质进行证明:
- (1)若x(n)的Z变换为X(z),则 ( − 1 ) n x ( n ) (-1)^{n}x(n) (−1)nx(n)的Z变换为 X(-z)
- (2)若x(n)的Z变换为X(z),则 x(-n)的Z变换为 X ( 1 z ) X(\frac{1}{z}) X(z1)
- (3)若x(n)的Z变换为X(z),则下x(2n)的Z变换为 1 2 [ X ( z 1 2 ) + X ( − z 1 2 ) ] \frac{1}{2}[X(z^\frac{1}{2})+X(-z^\frac{1}{2})] 21[X(z21)+X(−z21)]
证明:已知x(n)的Z变换为: X ( Z ) = ∑ − ∞ ∞ x ( n ) z − n X(Z)=\sum_{-\infty}^{\infty}{x(n)z^{-n}} X(Z)=∑−∞∞x(n)z−n-
( − 1 ) n x ( n ) {(-1)}^nx(n) (−1)nx(n)的Z变换为:
∑ − ∞ ∞ ( − 1 ) n x ( n ) z − n = ∑ − ∞ ∞ ( − 1 ) − n x ( n ) z − n = ∑ − ∞ ∞ x ( n ) ( − z ) − n = X ( − z ) \sum_{-\infty}^{\infty}{\left(-1\right)^{n}x\left(n\right)z^{-n}}=\sum_{-\infty}^{\infty}{\left(-1\right)^{-n}x\left(n\right)z^{-n}}=\sum_{-\infty}^{\infty}{x\left(n\right)\left(-z\right)^{-n}}=X\left(-z\right) ∑−∞∞(−1)nx(n)z−n=∑−∞∞(−1)−nx(n)z−n=∑−∞∞x(n)(−z)−n=X(−z) -
x(-n)的Z变换为:
∑ − ∞ ∞ x ( − n ) z − ( − n ) = ∑ − ∞ ∞ x ( − n ) ( z − 1 ) − n = X ( z − 1 ) = X ( 1 Z ) \sum_{-\infty}^{\infty}{x\left(-n\right)z^{-(-n)}}=\sum_{-\infty}^{\infty}{x\left(-n\right)\left(z^{-1}\right)^{-n}}=X\left(z^{-1}\right)=X\left(\frac{1}{Z}\right) ∑−∞∞x(−n)z−(−n)=∑−∞∞x(−n)(z−1)−n=X(z−1)=X(Z1)
x(2n)的Z变换为
∑ − ∞ ∞ x ( 2 n ) z − n \sum_{-\infty}^{\infty}{x\left(2n\right)z^{-n}} ∑−∞∞x(2n)z−n
令 k = 2 n k=2n k=2n
有 ∑ − ∞ ∞ x ( 2 n ) z − n = ∑ − ∞ ∞ x ( k ) z − k 2 \sum_{-\infty}^{\infty}{x\left(2n\right)z^{-n}}=\sum_{-\infty}^{\infty}{x\left(k\right)z^{-\frac{k}{2}}} ∑−∞∞x(2n)z−n=∑−∞∞x(k)z−2k
将 X ( z 1 2 ) = ∑ − ∞ ∞ x ( k ) z − k 2 X(z^{\frac{1}{2}})=\sum_{-\infty}^{\infty}{x\left(k\right)z^{-\frac{k}{2}}} X(z21)=∑−∞∞x(k)z−2k
X ( z − 1 2 ) = ∑ − ∞ ∞ x ( k ) ( − 1 ) k z − k 2 X(z^{-\frac{1}{2}})=\sum_{-\infty}^{\infty}{x\left(k\right)(-1)^{k}z^{-\frac{k}{2}}} X(z−21)=∑−∞∞x(k)(−1)kz−2k相加得
1 2 [ X ( z 1 2 ) + X ( − z 1 2 ) ] = ∑ − ∞ ∞ x ( k ) z − k 2 + ∑ − ∞ ∞ x ( k ) ( − 1 ) k z − k 2 = ∑ − ∞ ∞ x ( 2 n ) z − n \frac{1}{2}[X(z^\frac{1}{2})+X(-z^\frac{1}{2})]\\ =\sum_{-\infty}^{\infty}{x\left(k\right)z^{-\frac{k}{2}}}+\sum_{-\infty}^{\infty}{x\left(k\right)(-1)^{k}z^{-\frac{k}{2}}}\\=\sum_{-\infty}^{\infty}{x\left(2n\right)z^{-n}} 21[X(z21)+X(−z21)]=∑−∞∞x(k)z−2k+∑−∞∞x(k)(−1)kz−2k=∑−∞∞x(2n)z−n
-
3. 拉普拉斯旋转不变性证明
形式化描述什么是拉普拉斯算子,并证明拉普拉斯算子具有旋转不变性质
(二维平面内的旋转变换计算公式为 x ′ = x c o s θ − y s i n θ , y = x s i n θ + y c o s θ x'=xcosθ-ysinθ,y=xsinθ+ycosθ x′=xcosθ−ysinθ,y=xsinθ+ycosθ)
证明:

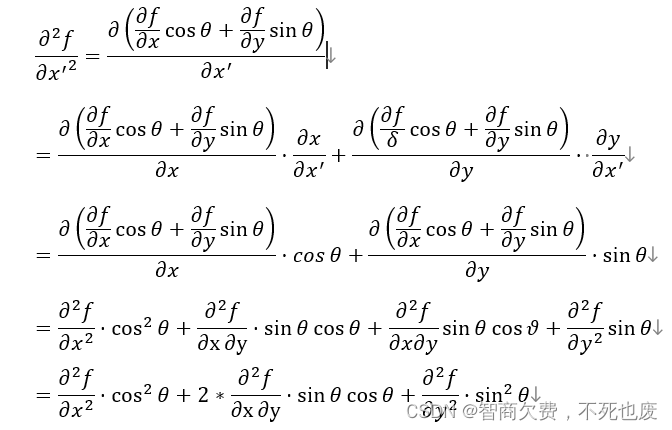
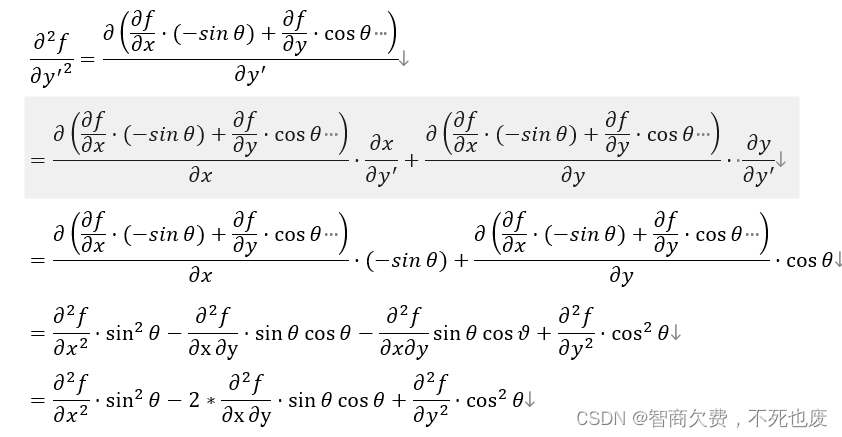

4.推导出随机数生成方程
假设我们有一个[0,1]上的均匀分布随机数发生器U(0,1), 请基于它构造指数分布的随机数发生器,推导出随机数生成方程。
若我们有一个标准正态分布的随机数发生器N(0,1),请推导出对数正态分布的随机数生成方程。
解: (1) 设U(0,1)可生成随机数 w ∈ [ 0 , 1 ] w\in [0,1] w∈[0,1],用它生成具有指数分布的随机数z,则其分布具有形式 F ( z ) = 1 − e − a z , z ≥ 0 F(z)=1-e^{-az},z\ge 0 F(z)=1−e−az,z≥0
令F(z)=w,解得: z = − 1 a l n [ 1 − U ( 0 , 1 ) ] z=-\frac{1}{a}ln[1-U(0,1)] z=−a1ln[1−U(0,1)]
(2) 设N(0,1)可生成随机数 w ∈ [ 0 , 1 ] w\in [0,1] w∈[0,1],用它生成具有正态分布的随机数z,则其分布具有形式 F ( z ) = ∫ 0 z 1 2 π b F(z)=\int_{0}^{z}\frac{1}{\sqrt{2\pi b}} F(z)=∫0z2πb1 e − [ l n ( v ) − a ] 2 2 b 2 d v e^{-\frac{[ln(v)-a]^{2}}{2b^{2}}}dv e−2b2[ln(v)−a]2dv
令F(z)=w,解得: z = e b w + a z=e^{bw+a} z=ebw+a
即 z = e b N ( 0 , 1 ) + a z=e^{bN(0,1)+a} z=ebN(0,1)+a
5. 快速小波变换分解与重建(2023秋)
在分析信号时小波分解与重建是一个重要的工具,离散 haar 小波是一种重要而简单J1/5 n=0.1的小波,它的尺度与小波向量分别为
- (1)现在假设我们有一个长度为8的信号f[1,-3,3,1,2,0,-2,1],利用快速哈尔小波变换进行三层的分解,计算各层的滤波器输出。
- (2)若利用哈尔小波对某个信号进行三层的分解的滤波器输出
W = [ W φ ( 1 , 0 ) , W φ ( 1 , 0 ) , W φ ( 2 , 0 ) , W φ ( 2 , 1 ) , W φ ( 3 , 0 ) , W φ ( 3 , 1 ) , W φ ( 3 , 2 ) , W φ ( 3 , 3 ) ] = [ 1 , 1 , − 1 , − 1 , 1 , 0 , 1 , 0 ] W=[W_{\varphi }(1,0),W_{\varphi }(1,0),W_{\varphi }(2,0),W_{\varphi }(2,1),W_{\varphi }(3,0),W_{\varphi }(3,1),W_{\varphi }(3,2),W_{\varphi }(3,3)]=[ 1,1,-1,-1,1,0,1,0] W=[Wφ(1,0),Wφ(1,0),Wφ(2,0),Wφ(2,1),Wφ(3,0),Wφ(3,1),Wφ(3,2),Wφ(3,3)]=[1,1,−1,−1,1,0,1,0],请计算重建原来的信号。
2023新增考点:算数编码与算数解码(2023未考)
对给出的编码模型信息进行解码0.23355
| 符号 | 概率 |
|---|---|
| a | 0.2 |
| e | 0.3 |
| i | 0.1 |
| o | 0.2 |
| u | 0.1 |
| ! | 0.1 |
解:根据概率将1划分成10份,a占0.2即[0,0.2),e占0.3即[0.2,0.5)以此类推得下面表格
| 符号 | 概率 | 范围 |
|---|---|---|
| a | 0.2 | [0.0,0.2) |
| e | 0.3 | [0.2,0.5) |
| i | 0.1 | [0.5,0.6) |
| o | 0.2 | [0.6,0.8) |
| u | 0.1 | [0.8,0.9) |
| ! | 0.1 | [0.9,1.0) |
0.2 < 0.23355 < 0.5 故第一位为e
将e的区间 [0.2,0.5) 划分成10份,每份为0.03,第一份为0.23
根据概率再次划分得
| 符号 | 概率 | 范围 |
|---|---|---|
| a | 0.2 | [0.2,0.26) |
| e | 0.3 | [0.26,0.35) |
| i | 0.1 | [0.35,0.38) |
| o | 0.2 | [0.38,0.44) |
| u | 0.1 | [0.44,0.47) |
| ! | 0.1 | [0.47,0.5) |
0.2 < 0.23355 < 0.26 故第二位为a
将a的区间 [0.2,0.26) 划分成10份,每份为0.006,第一份为0.206
根据概率再次划分得
| 符号 | 概率 | 范围 |
|---|---|---|
| a | 0.2 | [0.2,0.212) |
| e | 0.3 | [0.212,0.23) |
| i | 0.1 | [0.23,0.236) |
| o | 0.2 | [0.236,0.248) |
| u | 0.1 | [0.248,0.254) |
| ! | 0.1 | [0.254,0.26) |
0.23 < 0.23355 < 0.236 故第三位为i
将 i 的区间 [0.23,0.236) 划分成10份,每份为0.0006,第一份为0.2306
······
依次迭代最终得到“eaii!”
相关文章:

国科大图像处理2024速通期末——汇总2017-2019、2023回忆
国科大2023.12.28图像处理0854期末重点 图像处理 王伟强 作业 课件 资料 一、填空 一个阴极射线管它的输入与输出满足 s r 2 sr^{2} sr2,这将使得显示系统产生比希望的效果更暗的图像,此时伽马校正通常在信号进入显示器前被进行预处理,令p…...
)
编程笔记 html5cssjs 026 HTML输入类型(2/2)
编程笔记 html5&css&js 026 HTML输入类型(2/2) 输入类型:date输入类型:color输入类型:range输入类型:month输入类型:week输入类型:time输入类型:datetime输入类型…...
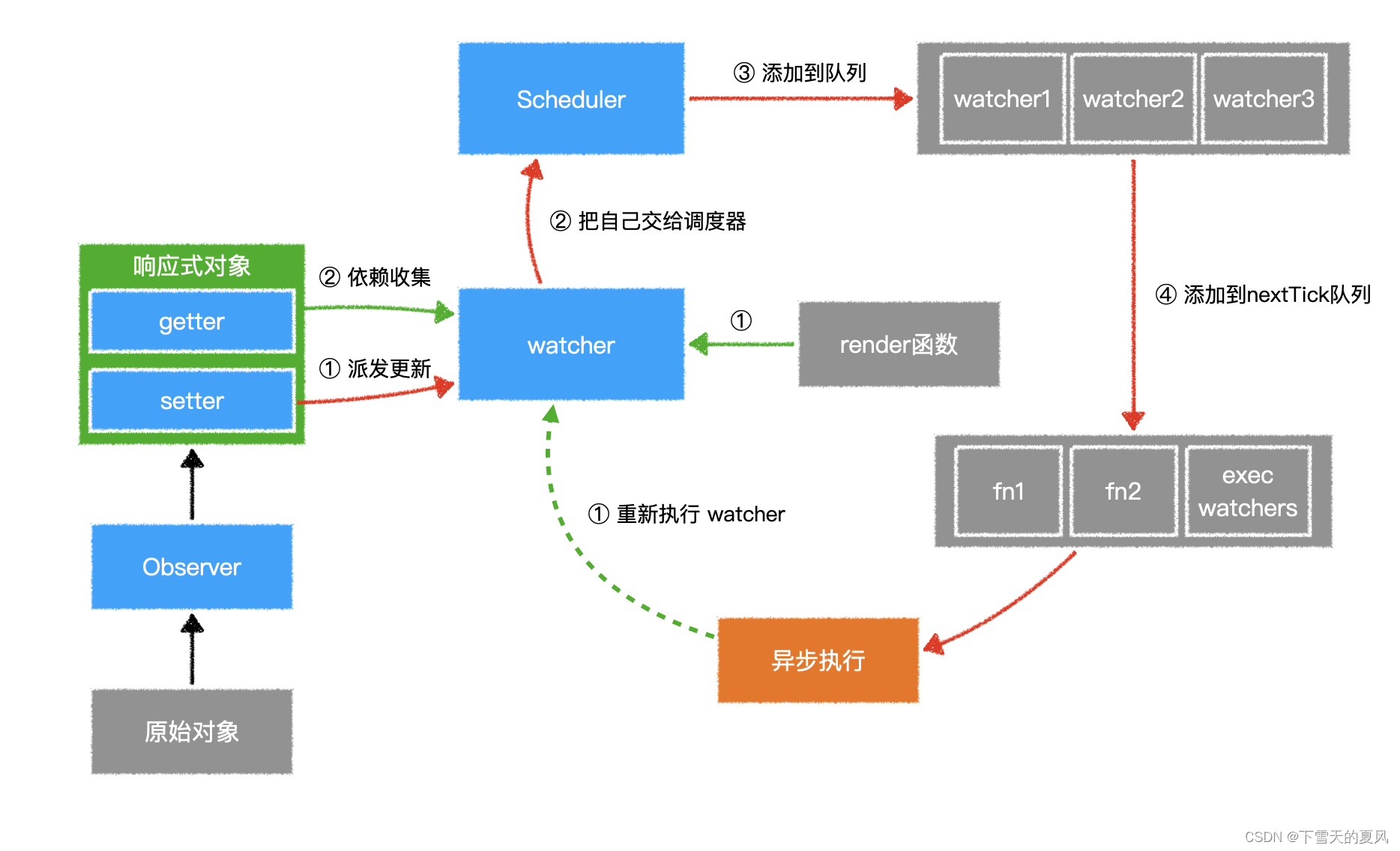
Vue2 - 数据响应式原理
目录 1,总览2,Observer3,Dep4,Watcher5,Schedule 1,总览 vue2官网参考 简单介绍下上图流程:以 Data 为中心来说, Vue 会将传递给 Vue 实例的 data 选项(普通 js 对象&a…...

基于华为云解析服务实现网站区域封禁
前言 中国大陆以外的网络攻击不断,个人博客时常遭受不明个人或组织的攻击,给网站的安全运行带来了巨大的风险,同时DDoS、CC攻击等还会消耗服务器的资源,站长可能需要因此支付高昂的服务器、CDN的流量费用。 因此,如果…...

在 Docker 中配置 MySQL 数据库并初始化 Project 项目
1. 文件准备 1.1. 添加 SQL 文件头部内容 每个 SQL 文件的头部需要添加以下内容: DROP DATABASE IF EXISTS xx_..; CREATE DATABASE xx_..; USE xx_..;1.2. 修改 AUTO_INCREMENT 在每个 SQL 文件中,将 AUTO_INCREMENT 修改为 1。 1.3. 插入机型 在 SQL…...
生活中的物理3——神奇陷阱(随机倒下的抽屉柜门)
1实验 材料:大自然(风)、抽屉门松掉的抽屉 实验 1、找一个大风的日子,打开窗户(不要找下雨天,不然你会被你亲爱的嫲嫲KO) 2、让风在抽屉面前刮过 3、你发现了什么??&…...

数模学习day08-拟合算法
这里拟合算法可以和差值算法对比 引入 插值和拟合的区别 与插值问题不同,在拟合问题中不需要曲线一定经过给定的点。拟 合问题的目标是寻求一个函数(曲线),使得该曲线在某种准则下与所 有的数据点最为接近,即曲线拟…...
第13课 利用openCV检测物体是否运动了
FFmpeg与openCV绝对是绝配。前面我们已经基本熟悉了FFmpeg的工作流程,这一章我们重点来看看openCV。 在前面,我们已经使用openCV打开过摄像头并在MFC中显示图像,但openCV能做的要远超你的想像,比如可以用它来实现人脸检测、车牌识…...
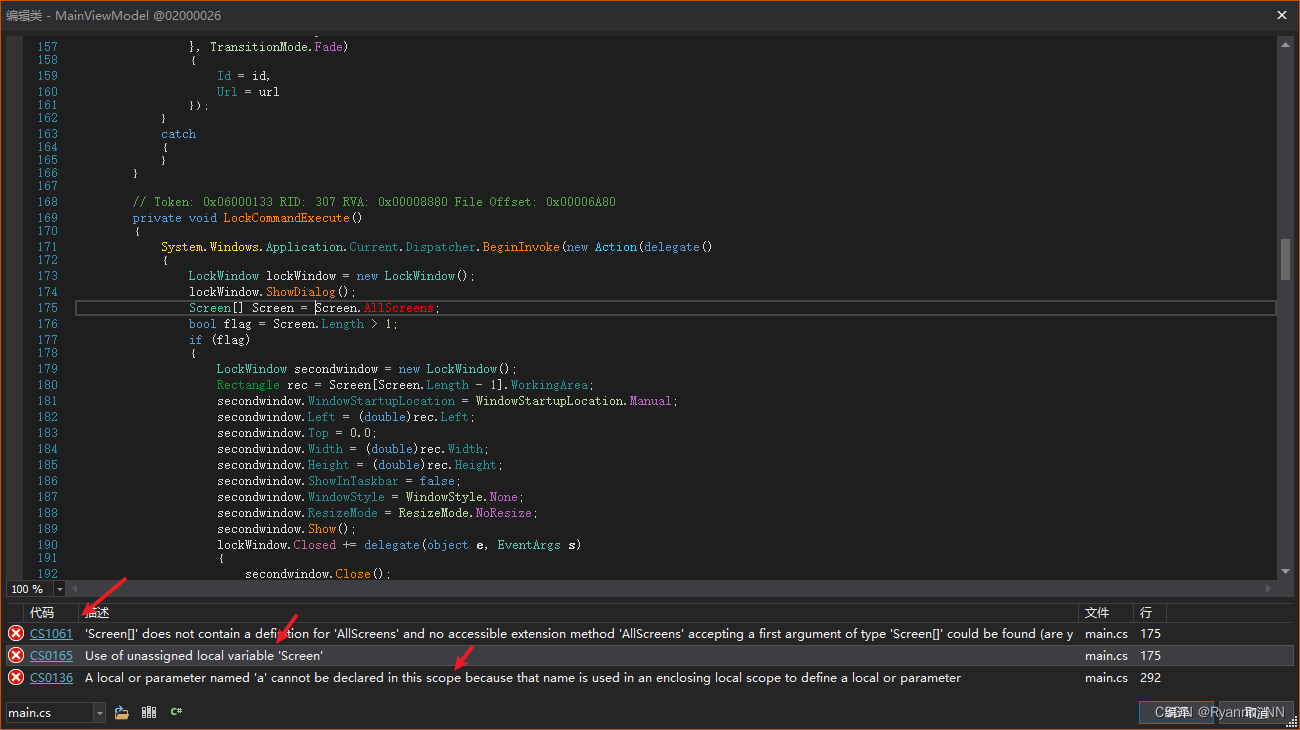
C#之反编译之路(一)
本文将介绍微软反编译神器dnSpy的使用方法 c#反编译之路(一) dnSpy.exe区分64位和32位,所以32位的程序,就用32位的反编译工具打开,64位的程序,就用64位的反编译工具打开(个人觉得32位的程序偏多,如果不知道是32位还是64位,就先用32位的打开试试) 目前只接触到wpf和winform的桌…...

使用CentOS 7.6搭建HTTP隧道代理服务器
在现代网络环境中,HTTP隧道代理服务器因其灵活性和安全性而受到广泛关注。CentOS 7.6,作为一个稳定且功能强大的Linux发行版,为搭建此类服务器提供了坚实的基础。 首先,我们需要明确HTTP隧道代理的基本原理。HTTP隧道代理允许客户…...

Swift爬虫使用代理IP采集唯品会商品详情
目录 一、准备工作 二、代理IP的选择与使用 三、使用Swift编写唯品会商品爬虫 四、数据解析与处理 五、注意事项与优化建议 六、总结 一、准备工作 在开始编写爬虫之前,需要准备一些工具和库,以确保数据抓取的顺利进行。以下是所需的工具和库&…...
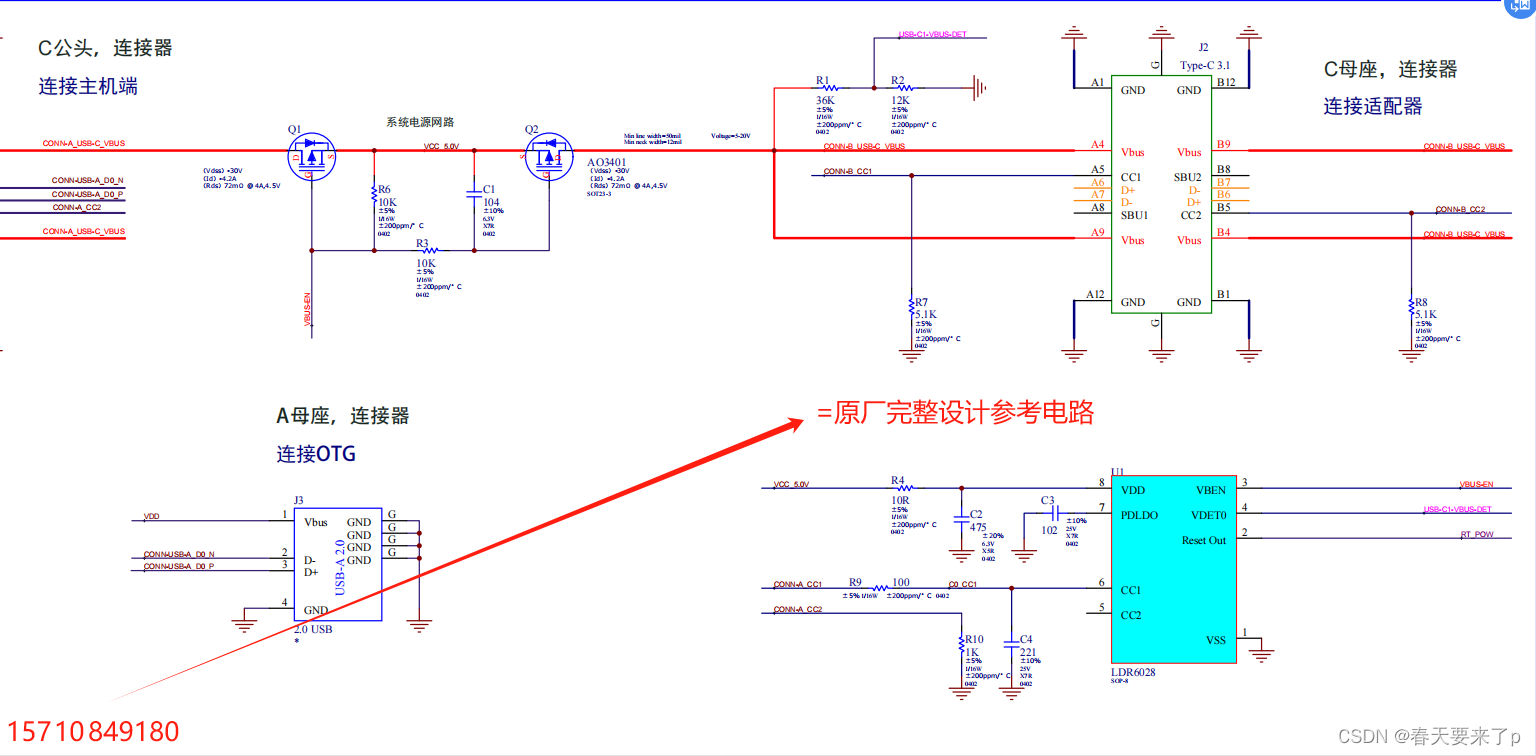
高性价比LDR6028Type-C转3.5mm音频和PD快充转接器
随着市面上的大部分手机逐渐取消了3.5mm音频耳机接口,仅保留一个Type-C接口,追求音质和零延迟的用户面临着一大痛点。对于这些用户,Type-C转3.5mm接口线的出现无疑是一大福音。这款线材在刚推出时就受到了手机配件市场的热烈欢迎,…...
【Docker】docker 服务相关命令
目录 1. 启动docker 服务 2.查看docker 服务的状态 3. 停止docker 服务 4.重启 docker 服务 5.开机自启动命令 1. 启动docker 服务 systemctl start docker 2.查看docker 服务的状态 systemctl status docker 3. 停止docker 服务 systemctl stop docker 此时再使用 syst…...

基于SpringBoot的在线问卷调查系统
文章目录 项目介绍主要功能截图:部分代码展示设计总结项目获取方式🍅 作者主页:超级无敌暴龙战士塔塔开 🍅 简介:Java领域优质创作者🏆、 简历模板、学习资料、面试题库【关注我,都给你】 🍅文末获取源码联系🍅 项目介绍 基于SpringBoot的在线问卷调查系统,java…...

智能分析网关V4太阳能风光互补远程视频智能监控方案
一、背景需求 在一些偏远地区,也具有视频监控的需求。但是这类场景中,一般无法就近获取市电,如果要长距离拉取市电,建设的成本非常高且长距离传输有安全隐患,因此风光互补远程视频监控方案的需求也较多。利用风光电转化…...

250:vue+openlayers 加载geotiff文件,并在地图上显示
第250个 点击查看专栏目录 本示例的目的是介绍演示如何在vue+openlayers中加载geotiff文件,并在地图上显示。这里使用到了WebGLTile图层和GeoTIFF脚本模块。这里一定要注意GeoTIFF的数据加载方式,要数组的模式。 直接复制下面的 vue+openlayers源代码,操作2分钟即可运行实现…...

【JavaEE】多线程(7) -- 线程池的概念和简单实现
目录 1.线程池是什么 2.标准库中的线程池 2.1ThreadPoolExecutor 2.2构造方法参数介绍 2.3拒绝策略(面试易考) 2.4Executor的使用 3.实现线程池 1.线程池是什么 线程池是一种用来管理线程的机制,它可以有效地控制线程的创建、复用和销毁,从而提高程…...

集合基础知识点
集合基础 1. 集合的由来 当 Java 程序中需要存放数据的时候,通常会定义变量来实现数据的存储,但是,当需要存储大量数据的时候该怎么办呢?这时首先想到的是数组,但是!数组只能存放同一类型的数据ÿ…...
最新版付费进群系统源码 /同城定位付费进群源码 /自带定位完整版/后台分销站点
源码介绍: 最新版付费进群系统源码 ,它是同城定位付费进群源码,而且自带定位完整版和后台分销站点。 看到有些人分享一些虚假的内容或者缺少文件的内容。现在分享完整给大家,功能是完整的。它是同城定位付费进群源码。 功能&am…...
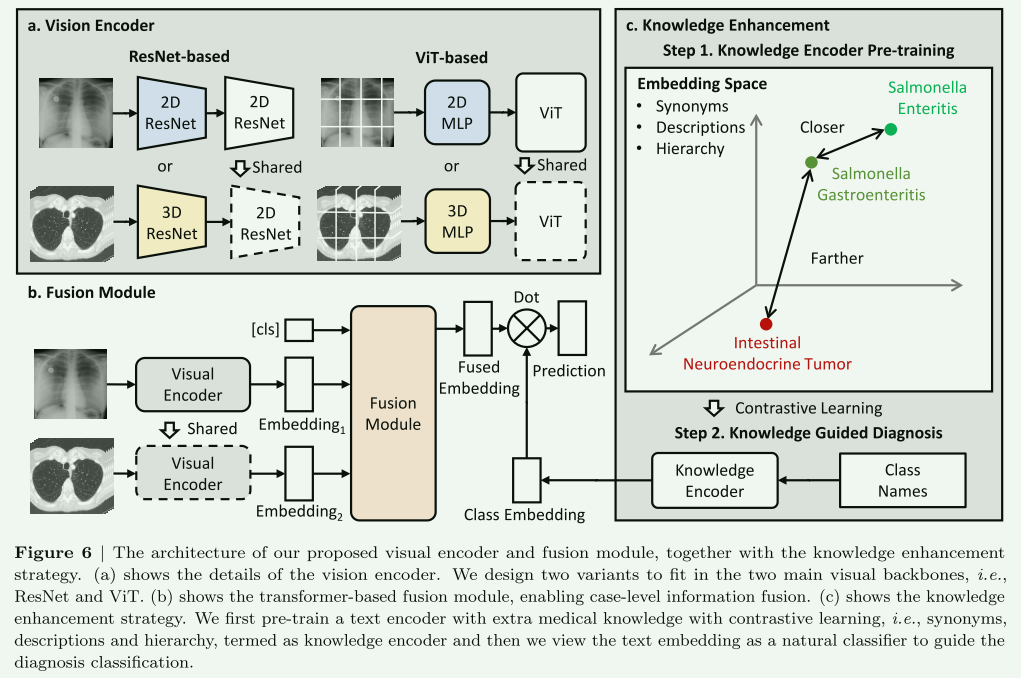
【论文阅读笔记】医学多模态新数据集-Large-scale Long-tailed Disease Diagnosis on Radiology Images
这是复旦大学2023.12.28开放出来的数据集和论文,感觉很宝藏,稍微将阅读过程记录一下。 Zheng Q, Zhao W, Wu C, et al. Large-scale Long-tailed Disease Diagnosis on Radiology Images[J]. arXiv preprint arXiv:2312.16151, 2023. 项目主页…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

从物理机到云原生:全面解析计算虚拟化技术的演进与应用
前言:我的虚拟化技术探索之旅 我最早接触"虚拟机"的概念是从Java开始的——JVM(Java Virtual Machine)让"一次编写,到处运行"成为可能。这个软件层面的虚拟化让我着迷,但直到后来接触VMware和Doc…...

从实验室到产业:IndexTTS 在六大核心场景的落地实践
一、内容创作:重构数字内容生产范式 在短视频创作领域,IndexTTS 的语音克隆技术彻底改变了配音流程。B 站 UP 主通过 5 秒参考音频即可克隆出郭老师音色,生成的 “各位吴彦祖们大家好” 语音相似度达 97%,单条视频播放量突破百万…...
