Mysql为什么只能支持2000w左右的数据量?
首先说明一下:
MySQL并没有硬性规定只能支持到2000万左右的数据量。
其实,MySQL能够处理的数据量远远超过这个数字。无论是开源社区版还是商业版,
MySQL在适当的硬件和配置下,都能够支持非常大的数据集。
通常所说的“MySQL只能支持2000万左右的数据量”,是在谈论具体的一些使用场景时大概的估算值,
受到某些配置、硬件资源或设计上的限制。在这些情况下,MySQL的性能可能会遇到瓶颈。
这些瓶颈可能来自于硬件限制、表结构设计、配置不当、查询优化、并发处理等。

2000万的数据量是如何估算的?
这里就不得提及数据库索引的构建,以及InnoDB存储引擎的结构和它是如何存储数据与索引的了。
索引的构建
索引是数据库中的一个数据结构,可以帮助快速定位到表中特定行的记录,就像书的目录能帮助你快速找到某个主题的章节一样。在MySQL的InnoDB存储引擎中,索引通常是使用B-Tree(具体来说是B+Tree)数据结构来构建的。
构建索引的过程如下:
- 选择索引列:通常,你会为表中的主键、经常用于查询条件(WHERE子句)的列、经常参与连接操作的列(JOIN条件)或者是经常需要排序和分组的列(ORDER BY、GROUP BY子句)创建索引。
- 确定索引类型:可以是单列索引,也可以是多列组合索引。组合索引考虑列的顺序,这会影响其效率。
- 创建索引:使用SQL语句
CREATE INDEX或者在创建表的时候直接定义。 - InnoDB处理索引:InnoDB存储引擎会在后台创建并维护相应的B+Tree结构,每个索引都会对应一棵B+Tree。
InnoDB的结构
InnoDB是MySQL的默认存储引擎,它支持事务、行级锁定和外键。它的主要结构包括:
- 表空间(Tablespace):InnoDB使用表空间来存储数据和索引。表空间可以是单个文件(file-per-table模式)也可以是共享的(如ibdata文件)。
- 数据页(Data Page):InnoDB将数据存储在页中,通常大小为16KB。数据页按行记录组织。
- B+Tree索引结构:这种索引结构有几个特点——平衡的树形结构,所有的叶子节点都在同一层,叶子节点之间是双向链表,叶子节点包含所有数据信息。
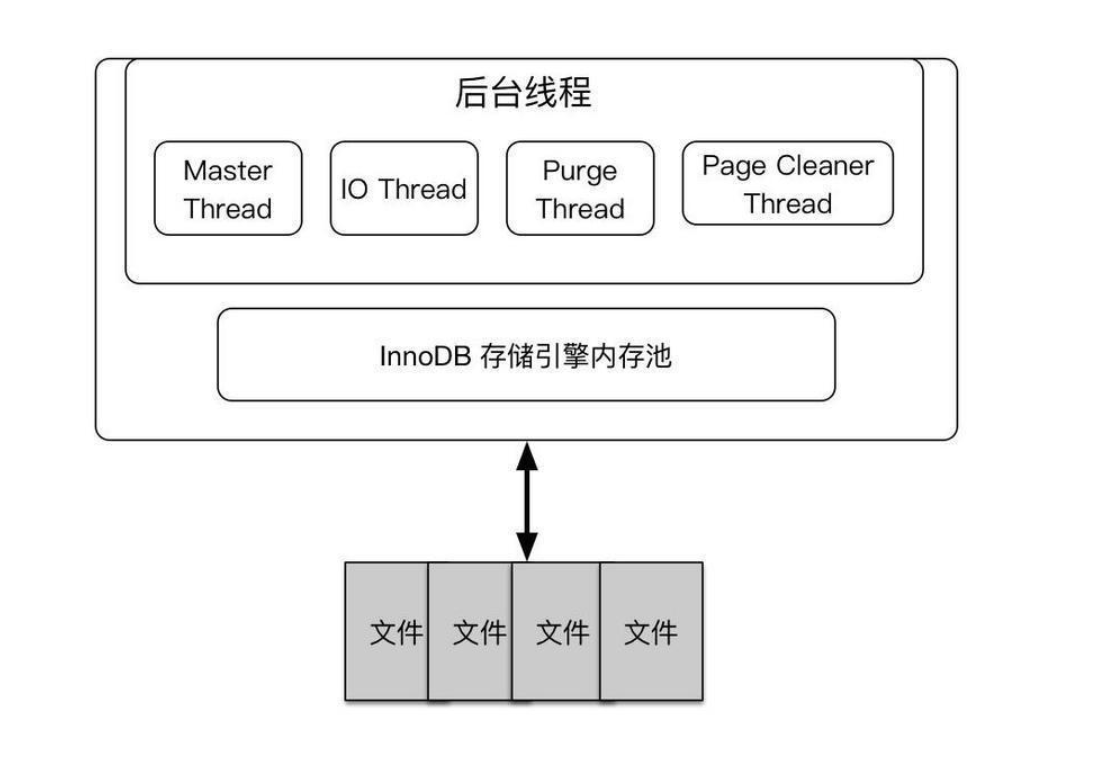
InnoDB如何存储数据与索引
在InnoDB中,表数据本身就是按照主键顺序存储的,这种结构被称为聚簇索引(Clustered Index)。每张表的聚簇索引是其主键索引,意味着表数据都存放在主键索引的B+Tree结构中的叶子节点上。如果表没有显式的主键,InnoDB会选择一个唯一索引代替;如果没有唯一索引,InnoDB会自动生成一个隐藏的row ID来作为主键。
对于非主键索引(也称为二级索引或辅助索引),叶子节点不直接存储行数据,而是存储相应行的主键值。当通过辅助索引查找数据时,会先在辅助索引的B+Tree中找到主键,然后再通过主键在聚簇索引中检索实际的行数据。
索引与2000万数据的关系
索引可以显著提高查询效率,尤其是在数据量大的表中。
但同时,索引也占用磁盘空间,并且在插入、更新和删除操作时需要额外的维护成本,因为不仅是数据本身,索引也需要相应地更新。
在数据库设计中,特别是当涉及到大量数据的时候,考虑B+树索引的层数是非常重要的。主键列被广泛使用bigint类型,这主要是因为bigint类型的整数范围很大(从-263到263-1),
能够支持极大量的数据行,这对于有大量数据的系统来说非常有用。
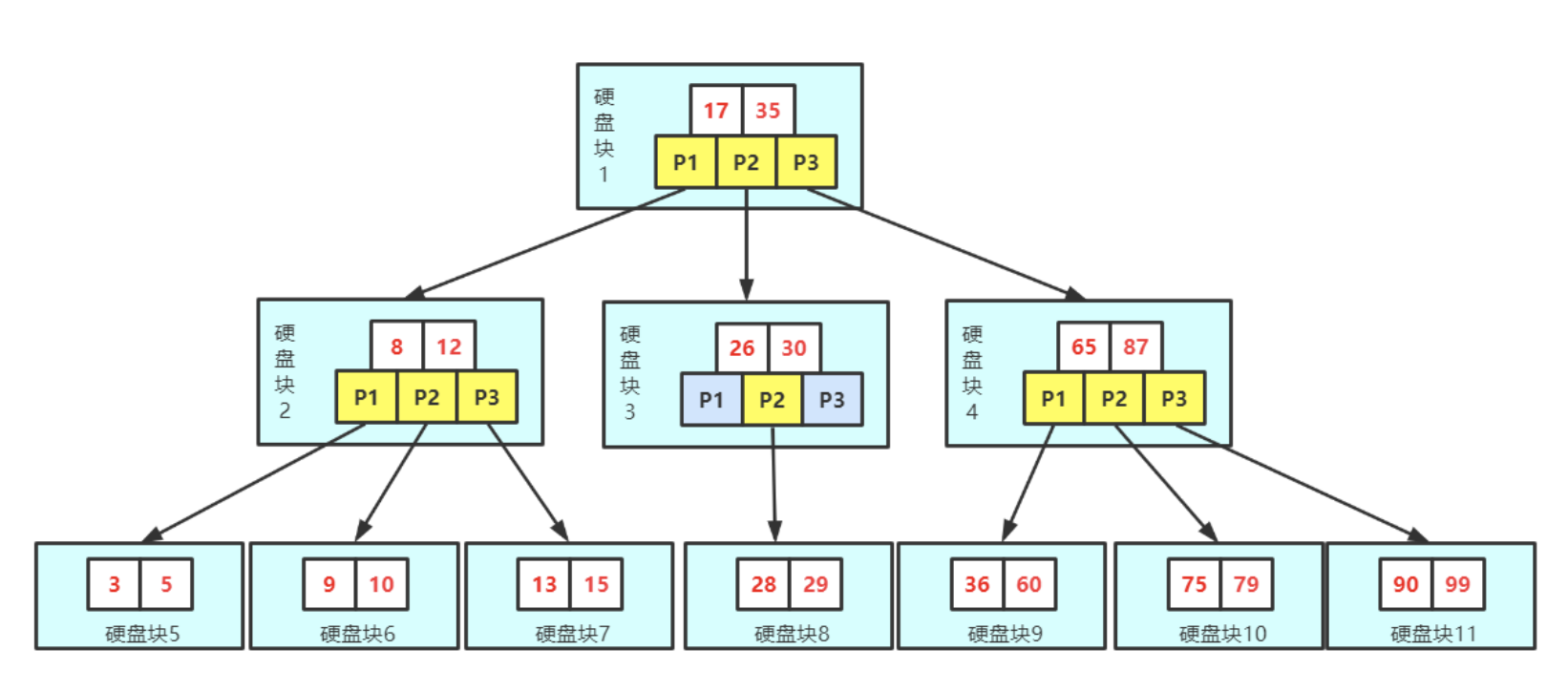
B+树索引层数的影响
B+树索引的层数决定了查询需要多少次磁盘I/O操作才能找到指定的数据。
理论上,B+树的每增加一层,就能够索引更多的数据,但同时也意味着访问数据时需要更多的磁盘访问次数。
因此,数据库系统通常尽可能地减少这些层数。
如何估算B+树索引的层数
假设我们使用的是InnoDB存储引擎,一个页(Page)默认是16KB大小,而一个bigint类型的索引大约需要8字节(实际上可能更多一点,因为还包括了页的指针,假设为14字节)。我们可以大概估算一下:
- 首先算每个叶子结点能够存储的数据量(假设每条数据1k,那么每个page能存储16条,非叶子节点的上一层节点数 = 数据量 / 16)
- 然后,假设每个非叶子节点存储的节点数量是 x,那么第一层就是 x = 16384 / 14;第二层就是,x的平方,三层就是x的三次方,以此类推
- 计算值与非叶子节点的上一层节点数比较即可得到层数
为何MySQL建议树的层数不超过三层?
B+树的层数建议限制在3层以内,主要是基于性能的考虑。当B+树的层数增加时,每次查询数据所需的磁盘I/O次数也会增加,因为每一层都可能涉及到一次磁盘I/O(尽管数据库的缓存机制可以减少这种情况发生的频率)。磁盘I/O通常比CPU计算和内存访问要慢得多,因此,为了维持数据库查询的高性能,建议尽量减少层数。
现在我们来估算一下三层B+树能存放多少索引条目。以InnoDB存储引擎为例,它的默认页大小是16KB(16384字节)。
我们假设现在数据库中的每一条数据为1k,每个索引条目大小为14字节(如果包含事务ID和回滚指针的话),
那么每个数据页假设存储16条数据。
下面是计算过程:
- 第一层:每个页可以存储的索引条目数为 16384 / 14 ≈ 1170 ,第一层有1170个叶子节点。
- 第二层:如果第二层也是完全填满的,那么它可以索引 1170 * 1170 ≈ 1368900, 第一层有1368900个叶子节点。
- 第三层(叶子节点):同理,第三层可以索引 1368900 * 16 ≈ 21902400 条数据。
这里是以bigint类型举例,当使用的类型不同时,存储的索引量不同,而且还与每行的数据大小有关。
总结
因此“2000万的数据量是如何估算的”这个说法是错误的,我们要根据自己的业务场景,具体情况具体分析。
可以使用预估的方式,计算在B+树的层数为3时,最大的数据量,当数据量远大于这个数值时,可以通过增加内存的方式,或者分库分表解决查询慢的情况。
最后说一句(求关注,求赞,别白嫖我)
最近无意间获得一份阿里大佬写的刷题笔记和面经,一下子打通了我的任督二脉,进大厂原来没那么难。
这是大佬写的, 7701页的阿里大佬写的刷题笔记,让我offer拿到手软
求一键三连:点赞、分享、收藏
点赞对我真的非常重要!在线求赞,加个关注我会非常感激!@小郑说编程
相关文章:

Mysql为什么只能支持2000w左右的数据量?
首先说明一下: MySQL并没有硬性规定只能支持到2000万左右的数据量。 其实,MySQL能够处理的数据量远远超过这个数字。无论是开源社区版还是商业版, MySQL在适当的硬件和配置下,都能够支持非常大的数据集。 通常所说的“MySQL只能…...
限制选中指定个数CheckBox控件(1/2)
限制选中指定个数CheckBox控件(1/2) 实例需求:工作表中有8个CheckBox控件(下文中简称为控件),现在需要实现限制用户最多只能勾选4个控件。 Dim OnDic As Object Sub CheckboxeEvent()Dim oCB As CheckBox…...
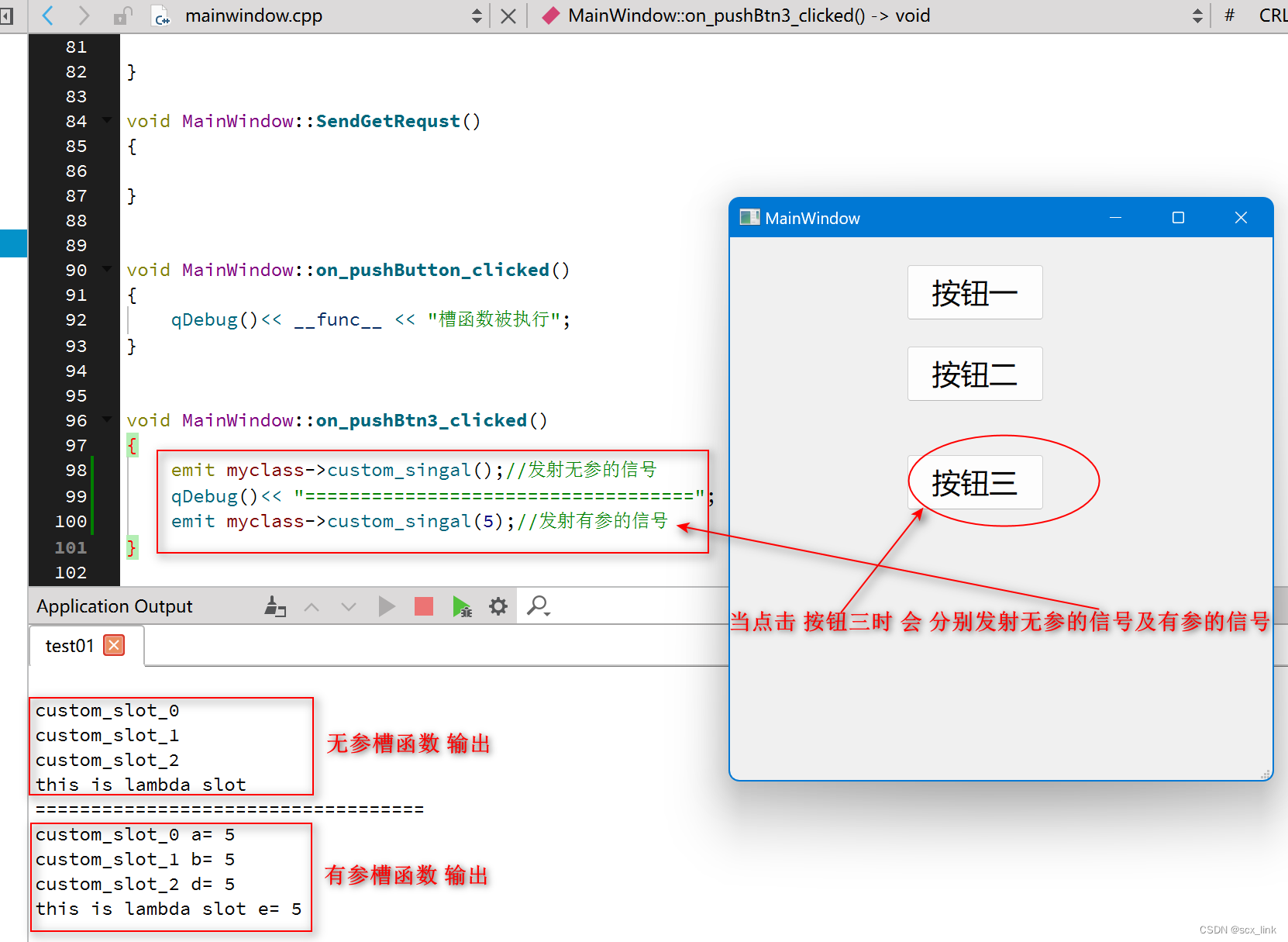
QT中的信号与槽的讲解
文章目录 信号及其特点槽及其特点代码演示标准信号与标准槽函数方式一方式二 自定义信号和槽connect()函数信号和槽函数存在函数重载的情况下Qt的信号槽机制注意事项 信号及其特点 信号:是一种特殊的函数,又称信号函数,俗称信号,…...

RNN文本分类任务实战
递归神经网络 (RNN): 定义:RNN 是一类专为顺序数据处理而设计的人工神经网络。 顺序处理:RNN 保持一个隐藏状态,该状态捕获有关序列中先前输入的信息,使其适用于涉及顺序依赖关系的任务。词嵌入…...

【算法系列 | 12】深入解析查找算法之—斐波那契查找
序言 心若有阳光,你便会看见这个世界有那么多美好值得期待和向往。 决定开一个算法专栏,希望能帮助大家很好的了解算法。主要深入解析每个算法,从概念到示例。 我们一起努力,成为更好的自己! 今天第12讲,讲…...

全新的C++语言
一、概述 C 的最初目标就是成为 “更好的 C”,因此新的标准首先要对基本的底层编程进行强化,能够反映当前计算机软硬件系统的最新发展和变化(例如多线程)。另一方面,C对多线程范式的支持增加了语言的复杂度࿰…...

three.js 多通道组合
效果: 代码: <template><div><el-container><el-main><div class"box-card-left"><div id"threejs" style"border: 1px solid red"></div><div style"border: 1px so…...

编程笔记 html5cssjs 022 HTML表单概要
编程笔记 html5&css&js 022 HTML表单概要 一、<form> 元素二、HTML Form 属性三、操作小结 网页光是输出没有输入可不行,因为输出还是比输入容易,所有就先接触输出,后学习输入。html用来输入的东西叫“表单”。 HTML 表单用于搜…...

三子棋(c语言)
前言: 三子棋是一种民间传统游戏,又叫九宫棋、圈圈叉叉棋、一条龙、井字棋等。游戏规则是双方对战,双方依次在9宫格棋盘上摆放棋子,率先将自己的三个棋子走成一条线就视为胜利。但因棋盘太小,三子棋在很多时候会出现和…...
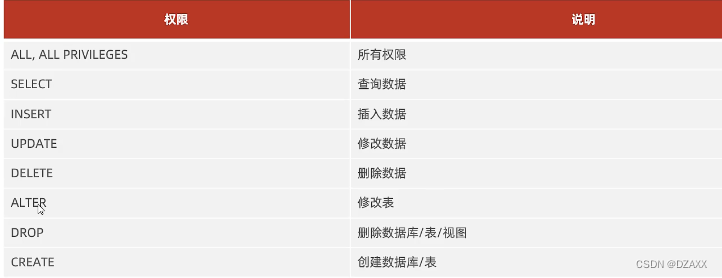
MySQL-DCL
DCL是数据控制语言,用来管理数据库用户,控制数据库的访问权限。 管理用户:管理哪些用户可以访问哪些数据库 1.查询用户 USE mysql; SELECT * FROM user; 注意: MySQL中用户信息和用户的权限信息都是记录在mysql数据库的user表中的…...

QT开源类库集合
QT开源类库集合 一、自定义控件 QSintQicsTableLongscroll-qtAdvanced Docking System 二、图表控件 QwtQCustomPlotJKQTPlotter 三、网络 QHttpEngineHTTP 四、 音视频 vlc-qt 五、多线程 tasks 六、数据库 EasyQtSql 一、自定义控件 1. QSint 源代码地址:QSint&…...
--算法(2))
C++ STL(2)--算法(2)
算法(2)----STL里的排序函数。 1. sort: 对容器或普通数组中指定范围内的元素进行排序,默认进行升序排序。 sort函数是基于快速排序实现的,属于不稳定排序。 只支持3种容器:array、vector、deque。 如果容器中存储的是自定义的对象ÿ…...
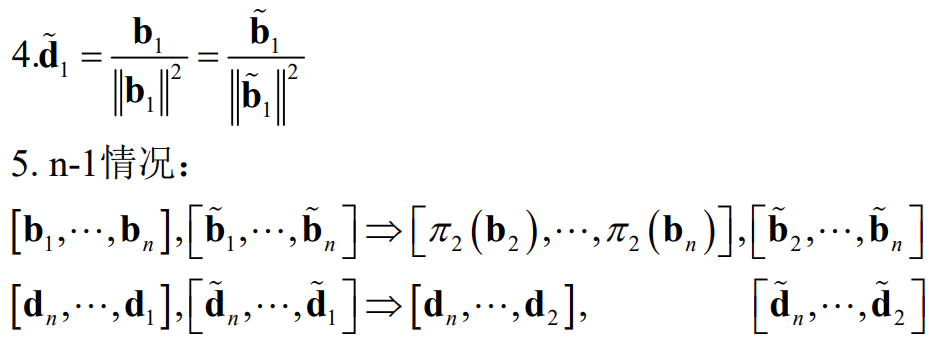
格密码基础:对偶格(超全面)
目录 一. 对偶格的格点 1.1 基本定义 1.2 对偶格的例子 1.3 对偶格的图形理解 二. 对偶格的格基 2.1 基本定义 2.2 对偶格的格基证明 三. 对偶格的行列式 3.1 满秩格 3.2 非满秩格 四. 重复对偶格 五. 对偶格的转移定理(transference theoremÿ…...

ECMAScript简介及特性
ECMAScript是一种由ECMA国际(前身为欧洲计算机制造商协会)制定和发布的脚本语言规范,JavaScript在它基础上进行了自己的封装。ECMAScript和JavaScript的关系是,前者是后者的规格,后者是前者的一种实现。 ECMAScript的…...
csdn中的资源文件如何删除?
csdn中的资源文件如何删除? 然后写文章的时候 点击资源绑定,解锁资源,就可以再次上传。...

NA原理及配置
在IP地址空间中,a;b;c类地址中各有一部分地址,被称为私有IP地址(私网地址),其余的为公有IP地址(公网地址) A:10.0.0.0 - 10.255.255.255 --- 相当于1条A类网段…...

解决:TypeError: ‘tuple’ object does not support item assignment
解决:TypeError: ‘tuple’ object does not support item assignment 文章目录 解决:TypeError: tuple object does not support item assignment背景报错问题报错翻译报错位置代码报错原因解决方法方法一:方法二:今天的分享就到…...
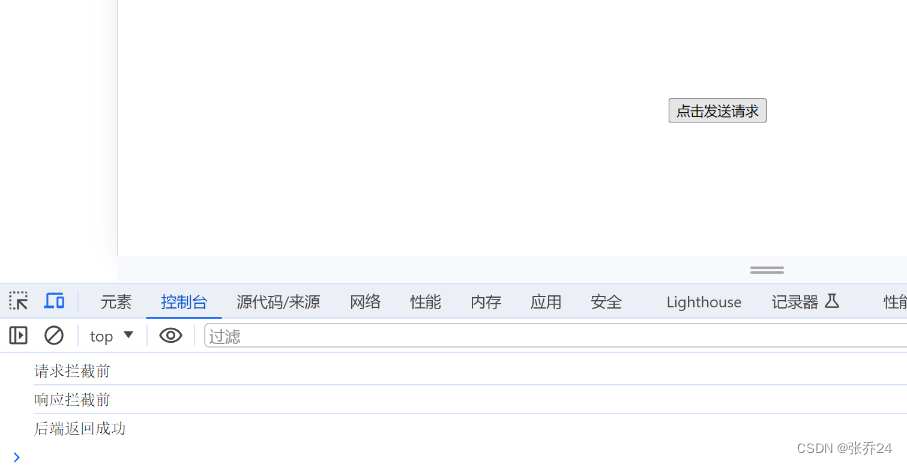
vue3项目中axios的常见用法和封装拦截(详细解释)
1、axios的简单介绍 Axios是一个基于Promise的HTTP客户端库,用于浏览器和Node.js环境中发送HTTP请求。它提供了一种简单、易用且功能丰富的方式来与后端服务器进行通信。能够发送常见的HTTP请求,并获得服务端返回的数据。 此外,Axios还提供…...

基础语法(一)(1)
常量和表达式 在这里,我们可以把Python当成一个计算器,来进行一些算术运算 例如: print(1 2 - 3) print(1 2 * 3) print(1 2 / 3)注意: print是一个python内置的函数,这个稍后我们会进行介绍 可以使用-*/&…...
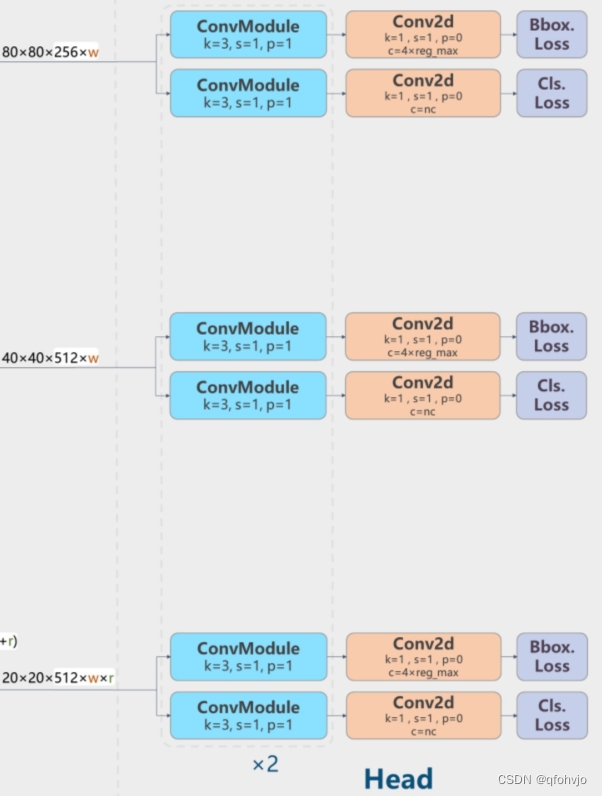
YOLOv8模型yaml结构图理解(逐层分析)
前言 YOLO-V8(官网地址):https://github.com/ultralytics/ultralytics 一、yolov8配置yaml文件 YOLOv8的配置文件定义了模型的关键参数和结构,包括类别数、模型尺寸、骨架(backbone)和头部(hea…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...

篇章二 论坛系统——系统设计
目录 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 1. 数据库设计 1.1 数据库名: forum db 1.2 表的设计 1.3 编写SQL 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 通过需求分析获得概念类并结合业务实现过程中的技术需要&#x…...

Vue3中的computer和watch
computed的写法 在页面中 <div>{{ calcNumber }}</div>script中 写法1 常用 import { computed, ref } from vue; let price ref(100);const priceAdd () > { //函数方法 price 1price.value ; }//计算属性 let calcNumber computed(() > {return ${p…...

uni-app学习笔记三十五--扩展组件的安装和使用
由于内置组件不能满足日常开发需要,uniapp官方也提供了众多的扩展组件供我们使用。由于不是内置组件,需要安装才能使用。 一、安装扩展插件 安装方法: 1.访问uniapp官方文档组件部分:组件使用的入门教程 | uni-app官网 点击左侧…...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...
