格密码基础:对偶格(超全面)
目录
一. 对偶格的格点
1.1 基本定义
1.2 对偶格的例子
1.3 对偶格的图形理解
二. 对偶格的格基
2.1 基本定义
2.2 对偶格的格基证明
三. 对偶格的行列式
3.1 满秩格
3.2 非满秩格
四. 重复对偶格
五. 对偶格的转移定理(transference theorem)
六. 对偶格的连续最小值
七. 对偶格的正交投影
八. 对偶格基的正交化
推荐先阅读:
格密码的基础概念-CSDN博客
一. 对偶格的格点
1.1 基本定义
对偶格(dual lattice)也被称之为倒易格(reciprocal lattice)。原来满秩的格写做,其对偶格的定义如下:
![]()
原来的格点和对偶格的任意(这两个字非常重要)格点相乘为整数即可。原来的格点如果为整数,那么对偶格里有可能会出现小数。此处代表n维实数空间,更准确来讲,对偶格应该在原来格的扩展空间内。那么对偶格更准确的定义,如下:
![]()
对偶格的右上角经常带“*”,代表格的扩展空间。
对偶格的重心在于,向量相乘为整数。当然,对偶格也是一种格,格的一些基本性质对偶格也具有。格和对偶格是成对出现的。
1.2 对偶格的例子
整数格的对偶格是其本身,也就是:
也就是整数格满足自对偶的性质。
如果把整数格的格点都扩大两倍,则形成子格。该格的对偶格则会出现小数,如下:
此处的系数有点类似倒数的感觉。
原始格的安全性在对偶格中依旧是存在的。
1.3 对偶格的图形理解
思考:给出任意一个向量点x,请找出所有跟这个向量点乘积为整数的点?
备注:向量与向量相乘为标量
线性代数告诉我们这些点会形成一个超平面,点跟点之间的距离为1/||x||。看一个二维的图形就很直接:
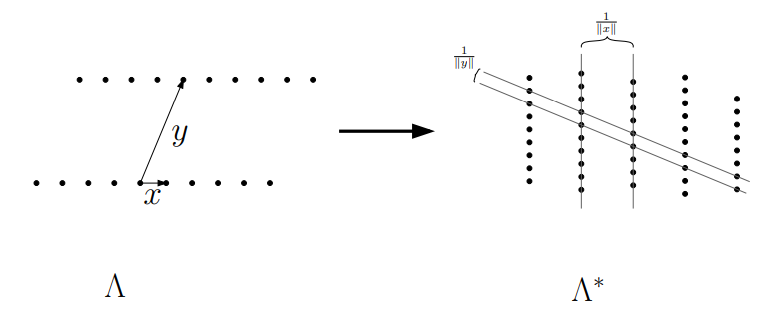
二. 对偶格的格基
格点相乘为整数,那这两个格的格基满足什么性质?
2.1 基本定义
原来的格基叫B,写做:
格基内每个向量都是m维,一共有n个向量。
对偶格的格基维度肯定是保持不变的,也就是:
对偶格和原来的格扩展空间肯定一致(向量点维度不一样的话,都不能相乘):
刚才发现对偶格有点倒数的感觉,反应在矩阵上则互逆,所以满足:
单位阵对角线上全为1,其他位置均为0。那么矩阵互逆告诉我们,向量位置一致时,相乘为1,也就是:
向量位置不一致时,相乘为0:
如果格基为方阵,也就是格满秩,则可以直接求逆,那么:
如果格基非方阵,也就是格非满秩,那么可以利用伪逆:
综合以上,对偶格的格基D需要满足两个性质:
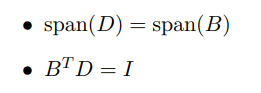
通过以上公式可以发现,只要B确定了,对偶格的格基D也是唯一确定的。
为什么格基满足如上性质,就可以是对偶格?请看2.2
2.2 对偶格的格基证明
本质就是需要证明:
借鉴集合相等的证明思路,我们的证明分成两步。
第一步:证明
从格L(B)内选取一个格点x,也就是,将其写做整数倍的向量求和形式:
从格基D中随机抽取一个向量,运算可得:
第一个等号:将格点x直接带入;
第二个等号:矩阵B与矩阵D互逆;
因为一定为整数,这个时候说明格基D中的每一个列向量都可以算做一个对偶格的格点。格点的求和运算具有封闭性,继续对这些对偶格点进行整数组合也一定是对偶格点,所以可得:
第二步:证明
从对偶格内随机取一个格点y,也就是:
根据对偶格的定义,易得:
根据扩展空间的定义,那么就可以将该点写做:
将对偶格的格点和原格的某个格基向量相乘,可得:
所以可得:
综上第一步和第二步,证明完毕。
三. 对偶格的行列式
对偶格的行列式与原来格的行列式互为倒数,也就是:
证明:
3.1 满秩格
将格基先转置在求逆,即为对偶格,所以可得:
逆矩阵的行列式与原矩阵的行列式互为倒数,所以可得:
矩阵转置不影响行列式的值,所以可得:
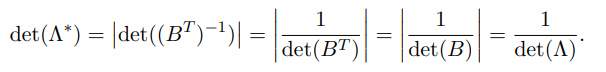
3.2 非满秩格
非满秩格不能直接求逆,则需要借助伪逆,运算性质与以上类似,可得:
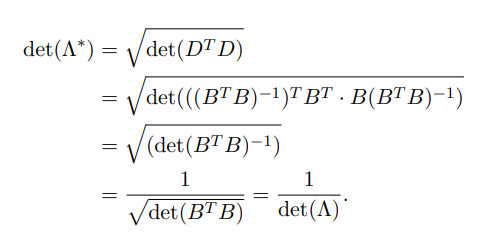
四. 重复对偶格
对偶格的对偶,即为原格,也就是:
证明:
考虑一般情况。记原格的格基为B,那么对偶格的格基为:
继续对格L(D)求对偶格,也就是运算:
带入运算可得:
![]()
五. 对偶格的转移定理(transference theorem)
本小节需要用到这篇博客的结论:
格密码与最短向量上界_最短向量问题-CSDN博客
假定格的秩为n,对偶格的最短向量长度满足:
证明:
首先根据闵可夫斯基上界(Minkowski's bound),可得:
![]()
将其类推到对偶格,可得:
![]()
两者相乘可得:
备注:根据Banaszczyk定理,这个界可以继续被放缩,可得:
六. 对偶格的连续最小值
本小节需要利用此篇博客的基础知识:
格密码基础:最短向量与连续最小值(附下界讨论)_格的逐次最小长度-CSDN博客
假定格的秩为n,可得:
证明:
假定v为原来的格最短的向量点,也就是:
从对偶格中取n个线性独立的向量:
根据格点相乘为整数,可得:
这两个向量的长度乘积必然大于1,也就是:
的长度一定比
要大,于是乎可得:
七. 对偶格的正交投影
对进行Gram-Schmidt正交化,可得:
其中代表将向量投影到前i-1个正交平面上,也就是:
假定B和D互为对偶格基。将矩阵B进行正交投影,可得:
此处就是把向量往同一个正交平面进行投影。
该格基的对偶格基与原来保持不变,也就是
证明:
从扩展平面角度来讲,可得:
根据对偶格基的性质。与
互相垂直,任意向量之间同样两两独立。换句话说,也就是:
所以可得:
满足对偶格基的第一个性质。
根据向量相乘的性质,不难计算:
![]()
根据逆矩阵的性质,不难证明原定理。
八. 对偶格基的正交化
原格基为:
Gram-Schmidt正交化为:
对偶格基:
按反方向,Gram-Schmidt正交化为:
长度满足:
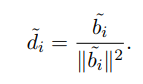
证明:通过以上对偶格基长度讨论易得。也可以用归纳法:
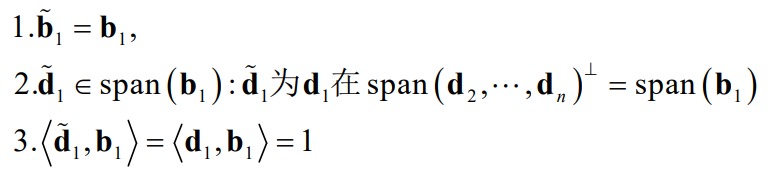
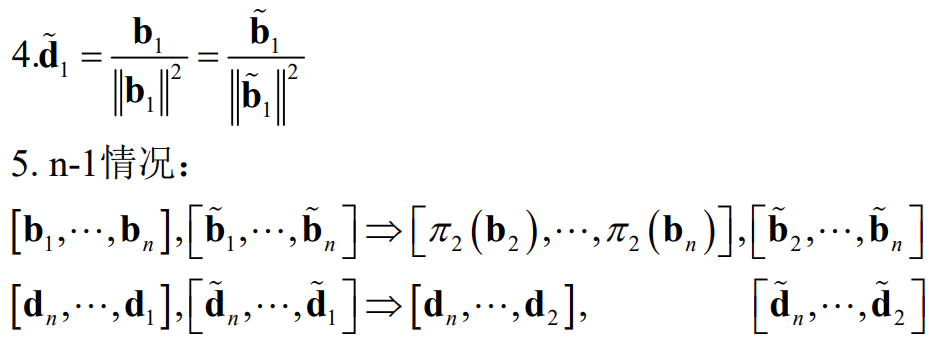
相关文章:
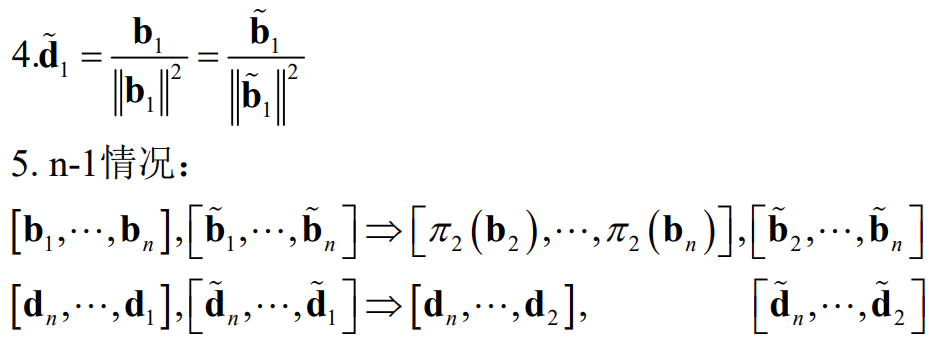
格密码基础:对偶格(超全面)
目录 一. 对偶格的格点 1.1 基本定义 1.2 对偶格的例子 1.3 对偶格的图形理解 二. 对偶格的格基 2.1 基本定义 2.2 对偶格的格基证明 三. 对偶格的行列式 3.1 满秩格 3.2 非满秩格 四. 重复对偶格 五. 对偶格的转移定理(transference theoremÿ…...

ECMAScript简介及特性
ECMAScript是一种由ECMA国际(前身为欧洲计算机制造商协会)制定和发布的脚本语言规范,JavaScript在它基础上进行了自己的封装。ECMAScript和JavaScript的关系是,前者是后者的规格,后者是前者的一种实现。 ECMAScript的…...
csdn中的资源文件如何删除?
csdn中的资源文件如何删除? 然后写文章的时候 点击资源绑定,解锁资源,就可以再次上传。...

NA原理及配置
在IP地址空间中,a;b;c类地址中各有一部分地址,被称为私有IP地址(私网地址),其余的为公有IP地址(公网地址) A:10.0.0.0 - 10.255.255.255 --- 相当于1条A类网段…...

解决:TypeError: ‘tuple’ object does not support item assignment
解决:TypeError: ‘tuple’ object does not support item assignment 文章目录 解决:TypeError: tuple object does not support item assignment背景报错问题报错翻译报错位置代码报错原因解决方法方法一:方法二:今天的分享就到…...
vue3项目中axios的常见用法和封装拦截(详细解释)
1、axios的简单介绍 Axios是一个基于Promise的HTTP客户端库,用于浏览器和Node.js环境中发送HTTP请求。它提供了一种简单、易用且功能丰富的方式来与后端服务器进行通信。能够发送常见的HTTP请求,并获得服务端返回的数据。 此外,Axios还提供…...

基础语法(一)(1)
常量和表达式 在这里,我们可以把Python当成一个计算器,来进行一些算术运算 例如: print(1 2 - 3) print(1 2 * 3) print(1 2 / 3)注意: print是一个python内置的函数,这个稍后我们会进行介绍 可以使用-*/&…...
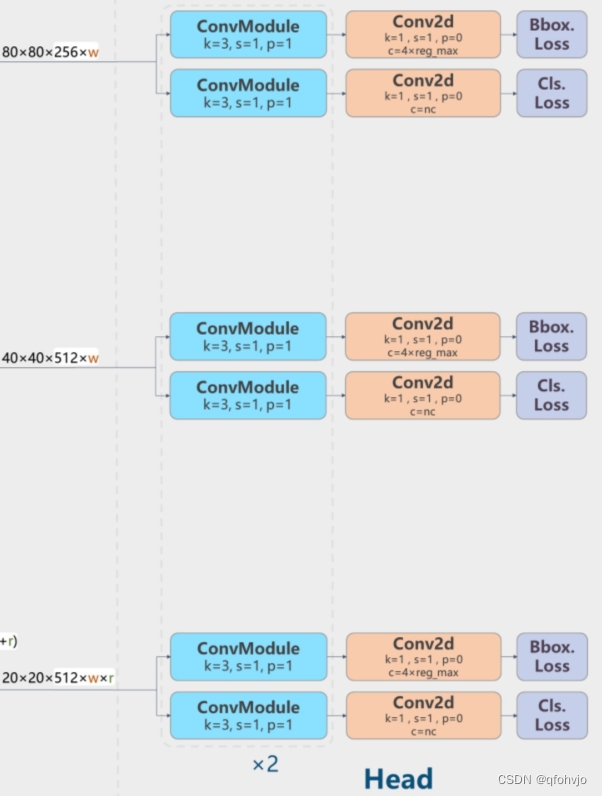
YOLOv8模型yaml结构图理解(逐层分析)
前言 YOLO-V8(官网地址):https://github.com/ultralytics/ultralytics 一、yolov8配置yaml文件 YOLOv8的配置文件定义了模型的关键参数和结构,包括类别数、模型尺寸、骨架(backbone)和头部(hea…...

【大数据】Zookeeper 集群及其选举机制
Zookeeper 集群及其选举机制 1.安装 Zookeeper 集群2.如何选取 Leader 1.安装 Zookeeper 集群 我们之前说了,Zookeeper 集群是由一个领导者(Leader)和多个追随者(Follower)组成,但这个领导者是怎么选出来的…...

Redis 过期策略
我们在set key的时候可以设置key的过期时间,哪redis是怎么处理过期的key的呢? 有三种过期策略 定时过期:每个设置过期时间的key会创建一个定时器,到过期时间就会立即对key进行清除。该策略可以立即清除过期的数据,对…...
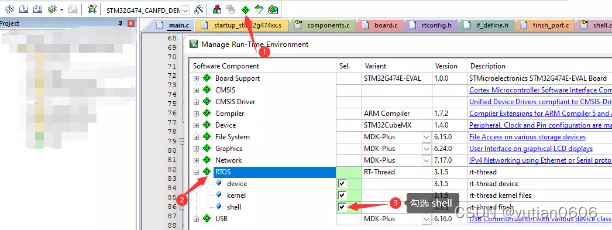
RT_Thread 调试笔记:串口打印、MSH控制台 相关
说明:记录日常使用 RT_Thread 开发时做的笔记。 持续更新中,欢迎收藏。 1.打印相关 1.打印宏定义,可以打印打印所在文件,函数,行数。 #define PRINT_TRACE() printf("-------%s:%s:%d------\r\n", __FIL…...
(适趣AI)Vue笔试题
📑前言 本文主要是【Vue】——(适趣AI)Vue笔试题的文章,如果有什么需要改进的地方还请大佬指出⛺️ 🎬作者简介:大家好,我是听风与他🥇 ☁️博客首页:CSDN主页听风与他 …...
)
Matytype的安装问题(word及PPT报错问题)
特别针对:mathtype安装了多次,又卸载了多次的用户。 Word报弹错错误:参考 mathtype安装后,打开word出现没找到dll的错误,这个问题较好解决。 如何解决MathType兼容Office 2016-MathType中文网 PPT(PowerPoi…...
docker拉取镜像提示 remote trust data does not exist for xxxxxx
1、How can I be sure that I am pulling a trusted image from docker 2、docker: you are not authorized to perform this operation: server returned 401. 以上两个问题可以试试以下解决办法 DOCKER_CONTENT_TRUSTfalse 本人是使用jenkins部署自己的项目到docker容器出现…...

ElasticSearch Nested类型全文检索、聚合查询
ElasticSearch Nested类型全文检索、聚合查询 Nested类型全文检索 创建索引 PUT /products1 {"mappings": {"properties": {"fulltext": {"type": "text"},"name": {"type": "text","…...

专业级的渗透测试服务,助力航空业数字化安全启航
某知名航空公司是中国首批民营航空公司之一,运营国内外航线200多条,也是国内民航最高客座率的航空公司之一。在数字化发展中,该航空公司以数据驱动决策,通过精细化管理、数字创新和模式优化等方式,实现了精准营销和个…...

【docker】安装 Redis
查看可用的 redis版本 docker search redis拉取 redis最新镜像 docker pull redis:latest查看本地镜像 docker images创建挂在文件 mkdir -pv /test1/docker_volume/redis/datamkdir -pv /test1/docker_volume/redis/confcd /test1/docker_volume/redis/conf/touch redis.con…...

pinia的独立维护,统一导出及持久化
目录 1.说明及示例 2.注意 1.说明及示例 在src下创建store文件夹,在store文件夹下创建index.js文件,内容如下: import { createPinia } from "pinia"; // pinia的持久化 import piniaPluginPersistedstate from "pinia-pl…...

【AI视野·今日Robot 机器人论文速览 第六十七期】Mon, 1 Jan 2024
AI视野今日CS.Robotics 机器人学论文速览 Mon, 1 Jan 2024 Totally 16 papers 👉上期速览✈更多精彩请移步主页 Daily Robotics Papers MURP: Multi-Agent Ultra-Wideband Relative Pose Estimation with Constrained Communications in 3D Environments Authors A…...

FBL刷写
刷写 1、刷写需求的理解2、刷写流程2.1、预编程阶段:保证在编程阶段的动作能够正常操作,控制器给响应。整车功能不会出现问题 刷写某一控制器时,避免其他控制器集DTC,85控制DTC; 28 通信控制.保证总线负载率不要过高(下…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...
