《动手学深度学习》学习笔记 第5章 深度学习计算
本系列为《动手学深度学习》学习笔记
书籍链接:动手学深度学习
笔记是从第四章开始,前面三章为基础知道,有需要的可以自己去看看
关于本系列笔记: 书里为了让读者更好的理解,有大篇幅的描述性的文字,内容很多,笔记只保留主要内容,同时也是对之前知识的查漏补缺
5. 深度学习计算
5.1 层和块
图5.1.1: 多个层被组合成块,形成更大的模型

下面的代码生成一个网络:具有256个单元和ReLU激活函数的全连接隐藏层,然后是一个具有10个隐藏单元且不带激活函数的全连接 输出层。
import torch
from torch import nn
from torch.nn import functional as F
net = nn.Sequential(nn.Linear(20, 256), nn.ReLU(), nn.Linear(256, 10))
X = torch.rand(2, 20)
net(X)
简而言 之,nn.Sequential定义了一种特殊的Module,即在PyTorch中表示一个块的类,它维护了一个由Module组成 的有序列表。
这个前 向传播函数非常简单:它将列表中的每个块连接在一起,将每个块的输出作为下一个块的输入。
5.1.1 自定义块
从零开始编写一个块:它包含一个多层感知机,其具有256个隐藏单元的隐藏层和一 个10维输出层。
class MLP(nn.Module):# 用模型参数声明层。这里,我们声明两个全连接的层def __init__(self):# 调用MLP的父类Module的构造函数来执行必要的初始化。# 这样,在类实例化时也可以指定其他函数参数,例如模型参数params(稍后将介绍)super().__init__()self.hidden = nn.Linear(20, 256) # 隐藏层self.out = nn.Linear(256, 10) # 输出层# 定义模型的前向传播,即如何根据输入X返回所需的模型输出def forward(self, X):# 注意,这里我们使用ReLU的函数版本,其在nn.functional模块中定义。return self.out(F.relu(self.hidden(X)))
- 首先, 我们定制的__init__函数通过super().init()调用父类的__init__函数(省去了重复编写模版代码的痛苦。)
- 然后,我们实例化两个全连接层,分别为self.hidden和self.out。
- 注意,除非我们实现一个新的运算符, 否则我们不必担心反向传播函数或参数初始化,系统将自动生成这些。
5.1.2 顺序块
看看Sequential类是如何工作的?
为了构建我们自己的简化的MySequential,我们只需要定义两个关键函数:
- 将块逐个追加到列表中的函数;
- 前向传播函数,用于将输入按追加块的顺序传递给块组成的“链条”。
class MySequential(nn.Module):def __init__(self, *args):super().__init__()for idx, module in enumerate(args):# 这里,module是Module子类的一个实例。我们把它保存在'Module'类的成员# 变量_modules中。_module的类型是OrderedDictself._modules[str(idx)] = moduledef forward(self, X):# OrderedDict保证了按照成员添加的顺序遍历它们for block in self._modules.values():X = block(X)return X
- __init__函数将每个模块逐个添加到有序字典_modules中。
为什么每个Module都有一 个_modules属性?
为什么我们使用它而不是自己定义一个Python列表?
.
简而言之,_modules的主要优点是:在模块的参数初始化过程中,系统知道在_modules字典中查找需要初始化参数的子块。
5.1.3 在前向传播函数中执行代码
有时我们可能希望合并 既不是上一层的结果也不是可更新参数的项,我们称之为常数参数(constant parameter)。
例如,我们需要一个计算函数 f ( x , w ) = c ⋅ w ⊤ x f(x, w) = c · w^{⊤}x f(x,w)=c⋅w⊤x的层,其中x是输入, w w w是参数, c c c是某个在优化过程中没有更新的指定常量。因此我们实现了一个FixedHiddenMLP类,如下所示:
class FixedHiddenMLP(nn.Module):def __init__(self):super().__init__()# 不计算梯度的随机权重参数。因此其在训练期间保持不变self.rand_weight = torch.rand((20, 20), requires_grad=False)self.linear = nn.Linear(20, 20)def forward(self, X):X = self.linear(X)# 使用创建的常量参数以及relu和mm函数X = F.relu(torch.mm(X, self.rand_weight) + 1)# 复用全连接层。这相当于两个全连接层共享参数X = self.linear(X)# 控制流while X.abs().sum() > 1:X /= 2return X.sum()
其中权重(self.rand_weight)在实例化时被随机初始化,之后为常量。这个权重不是一个模型参数,因此它不会被反向传播更新。
5.2 参数管理
在选择了架构并设置了超参数后,我们就进入了训练阶段。
- 此时,我们的目标是找到使损失函数最小化的模型参数值。经过训练后,我们将需要使用这些参数来做出未来的预测。
- 此外,有时我们希望提取参数,以便在其他环境中复用它们,将模型保存下来,以便它可以在其他软件中执行,或者为了获得科学的理解而进行检查。
本节,我们将介绍以下内容:
- 访问参数,用于调试、诊断和可视化;
- 参数初始化;
- 在不同模型组件间共享参数。
5.2.1 参数访问
从已有模型中访问参数。当通过Sequential类定义模型时,可以通过索引来访问模型的任意层。
如下所示,我们可以检查第二个全连接层的参数。
print(net[2].state_dict())OrderedDict([('weight', tensor([[-0.0427, -0.2939, -0.1894, 0.0220, -0.1709, -0.1522, -0.0334, -0.,2263]])), ('bias', tensor([0.0887]))])
输出的结果:
- 首先,这个全连接层包含两个参数,分别是该层的权重和偏置。
- 两者都存储为单精度浮点数(float32)。
注意,参数名称允许唯一标识每个参数,即使在包含数百个层的网络中也是如此。
目标参数
访问底层的数值:从第二个全连接层(即第三个神经网络层)提取偏置,提取后返回的是一个参数类实例,并进一步访问该参数的值。
print(type(net[2].bias))
print(net[2].bias)
print(net[2].bias.data)
参数是复合的对象,包含值、梯度和额外信息。 除了值之外,我们还可以访问每个参数的梯度。(在上面这个网络中,由于我们还没有调用反向传播,所以参数的梯度处于初始状态。)
一次性访问所有参数
当我们需要对所有参数执行操作时,逐个访问它们可能会很麻烦。当我们处理更复杂的块(例如,嵌套块)
时,情况可能会变得特别复杂,因为我们需要递归整个树来提取每个子块的参数。下面,我们将通过演示来
比较访问第一个全连接层的参数和访问所有层。
print(*[(name, param.shape) for name, param in net[0].named_parameters()])
# ('weight', torch.Size([8, 4])) ('bias', torch.Size([8]))print(*[(name, param.shape) for name, param in net.named_parameters()])
#('0.weight', torch.Size([8, 4])) ('0.bias', torch.Size([8]))
#('2.weight', torch.Size([1, 8])) ('2.bias', torch.Size([1]))
这为我们提供了另一种访问网络参数的方式,如下所示。
net.state_dict()['2.bias'].data
# tensor([0.0887])
从嵌套块收集参数
如果将多个块相互嵌套,参数命名约定是如何工作的?
def block1():return nn.Sequential(nn.Linear(4, 8), nn.ReLU(),nn.Linear(8, 4), nn.ReLU())def block2():net = nn.Sequential()for i in range(4):# 在这里嵌套net.add_module(f'block {i}', block1())return netrgnet = nn.Sequential(block2(), nn.Linear(4, 1))
rgnet(X)
print(rgnet)
Sequential(
(0): Sequential((block 0): Sequential((0): Linear(in_features=4, out_features=8, bias=True)(1): ReLU()(2): Linear(in_features=8, out_features=4, bias=True)(3): ReLU())(block 1): Sequential((0): Linear(in_features=4, out_features=8, bias=True)(1): ReLU()(2): Linear(in_features=8, out_features=4, bias=True)(3): ReLU())(block 2): Sequential((0): Linear(in_features=4, out_features=8, bias=True)(1): ReLU()(2): Linear(in_features=8, out_features=4, bias=True)(3): ReLU())(block 3): Sequential((0): Linear(in_features=4, out_features=8, bias=True)(1): ReLU()(2): Linear(in_features=8, out_features=4, bias=True)(3): ReLU()))
(1): Linear(in_features=4, out_features=1, bias=True))
rgnet[0][1][0].bias.data
# tensor([ 0.1999, -0.4073, -0.1200, -0.2033, -0.1573, 0.3546, -0.2141, -0.2483])
5.2.2 参数初始化
默认情况下,PyTorch会根据一个范围均匀地初始化权重和偏置矩阵,这个范围是根据输入和输出维度计算
出的。
PyTorch的nn.init模块提供了多种预置初始化方法:
内置初始化
- 例1:将所有权重参数初始化为标准差为0.01的高斯随机变量,且将偏置参数设置为0。
def init_normal(m):if type(m) == nn.Linear:nn.init.normal_(m.weight, mean=0, std=0.01)nn.init.zeros_(m.bias)
net.apply(init_normal)
net[0].weight.data[0], net[0].bias.data[0]
- 例2:将所有参数初始化为给定的常数,比如初始化为1。
def init_constant(m):if type(m) == nn.Linear:nn.init.constant_(m.weight, 1)nn.init.zeros_(m.bias)net.apply(init_constant)net[0].weight.data[0], net[0].bias.data[0]
- 例3:使用Xavier初始化方法初始化第一个神经网络层,然后将第三个神经网络层初始化为常量值42。
def init_xavier(m):if type(m) == nn.Linear:nn.init.xavier_uniform_(m.weight)def init_42(m):if type(m) == nn.Linear:nn.init.constant_(m.weight, 42)net[0].apply(init_xavier)
net[2].apply(init_42)
print(net[0].weight.data[0])
print(net[2].weight.data)
5.2.3 参数绑定
有时希望在多个层间共享参数:我们可以定义一个稠密层,然后使用它的参数来设置另一个层的参数。
# 我们需要给共享层一个名称,以便可以引用它的参数
shared = nn.Linear(8, 8)
net = nn.Sequential(nn.Linear(4, 8), nn.ReLU(),shared, nn.ReLU(),shared, nn.ReLU(),nn.Linear(8, 1))
net(X)
# 检查参数是否相同
print(net[2].weight.data[0] == net[4].weight.data[0])
net[2].weight.data[0, 0] = 100
# 确保它们实际上是同一个对象,而不只是有相同的值
print(net[2].weight.data[0] == net[4].weight.data[0])
这个例子表明第三个和第五个神经网络层的参数是绑定的(实际上是同一个对象)。它们不仅值相等,而且由相同的张量表示。因此,如果我们改变其中一个参数,另一个参数也会改变。
当参数绑定时,梯度会发生什么情况?
答案是由于模型参数包含梯度,因此在反向传播期间第二个隐藏层(即第三个神经网络层)和第三个隐藏层(即第五个神经网络层)的梯度会加在一起。
5.3 延后初始化
到目前为止,我们忽略了建立网络时需要做的以下这些事情:
- 定义了网络架构,但没有指定输入维度。
- 添加层时没有指定前一层的输出维度。
- 在初始化参数时,甚至没有足够的信息来确定模型应该包含多少参数。
深度学习框架无法判断网络的输入维度是什么。这里的诀窍是框架的延后初始化(defers initialization),即直到数据第一次通过模型传递时,框架才会动态地推断出每个层的大小。
5.3.1 实例化网络
首先,实例化一个多层感知机。
此时,因为输入维数是未知的,所以网络不可能知道输入层权重的维数。因此,框架尚未初始化任何参数。
接下来让将数据通过网络,最终使框架初始化参数。
一旦知道输入维数是20,框架可以通过代入值20来识别第一层权重矩阵的形状。识别出第一层的形状后,框架处理第二层,依此类推,直到所有形状都已知为止。
注意,在这种情况下,只有第一层需要延迟初始化,但是框架仍是按顺序初始化的。等到知道了所有的参数形状,框架就可以初始化参数。
5.4 自定义层
深度学习成功背后的一个因素是神经网络的灵活性:可以用创造性的方式组合不同的层,从而设计出适用于各种任务的架构。
5.4.1 不带参数的层
首先,构造一个没有任何参数的自定义层。
下面的CenteredLayer类要从其输入中减去均值。要构建它,我们只需继承基础层类并实现前向传播功能。
import torch
import torch.nn.functional as F
from torch import nnclass CenteredLayer(nn.Module):def __init__(self):super().__init__()def forward(self, X):return X - X.mean()
验证:
layer = CenteredLayer()
layer(torch.FloatTensor([1, 2, 3, 4, 5]))
# tensor([-2., -1., 0., 1., 2.])
net = nn.Sequential(nn.Linear(8, 128), CenteredLayer())
Y = net(torch.rand(4, 8))
Y.mean()
# tensor(7.4506e-09, grad_fn=<MeanBackward0>)
5.4.2 带参数的层
实现自定义版本的全连接层。该层需要两个参数,一个用于表示权重,另一个用于表示偏置项。
在此实现中,使用修正线性单元作为激活函数。该层需要输入参数:in_units和units,分别表示输入数和输出数。
class MyLinear(nn.Module):def __init__(self, in_units, units):super().__init__()self.weight = nn.Parameter(torch.randn(in_units, units))self.bias = nn.Parameter(torch.randn(units,))def forward(self, X):linear = torch.matmul(X, self.weight.data) + self.bias.datareturn F.relu(linear)
实例化MyLinear类并访问其模型参数。
linear = MyLinear(5, 3)
linear.weight
#Parameter containing:
#tensor([[ 0.1775, -1.4539, 0.3972],#[-0.1339, 0.5273, 1.3041],#[-0.3327, -0.2337, -0.6334],#[ 1.2076, -0.3937, 0.6851],#[-0.4716, 0.0894, -0.9195]], requires_grad=True)
5.5 读写文件
5.5.1 加载和保存张量
import torch
from torch import nn
from torch.nn import functional as Fx = torch.arange(4)
torch.save(x, 'x-file') # 保存x2 = torch.load('x-file') # 读取
以写入或读取从字符串映射到张量的字典。
mydict = {'x': x, 'y': y}
torch.save(mydict, 'mydict')
mydict2 = torch.load('mydict')
mydict2
5.5.2 加载和保存模型参数
class MLP(nn.Module):def __init__(self):super().__init__()self.hidden = nn.Linear(20, 256)self.output = nn.Linear(256, 10)def forward(self, x):return self.output(F.relu(self.hidden(x)))net = MLP()
X = torch.randn(size=(2, 20))
Y = net(X)
将模型的参数存储在一个叫做“mlp.params”的文件中。
torch.save(net.state_dict(), 'mlp.params')
为了恢复模型,我们实例化了原始多层感知机模型的一个备份。
这里我们不需要随机初始化模型参数,而是直接读取文件中存储的参数。
clone = MLP()
clone.load_state_dict(torch.load('mlp.params'))
clone.eval()
5.6 GPU
使用nvidia-smi命令查看显卡信息。
!nvidia-smi
5.6.1 计算设备
指定用于存储和计算的设备,如CPU和GPU。默认情况下,张量是在内存中创建的,然后使用CPU计算它。
应该注意的是:
- cpu设备意味着所有物理CPU和内存,这意味着PyTorch的计算将尝试使用所有CPU核心。
- 然而,gpu设备只代表一个卡和相应的显存。
- 如果有多个GPU,我们使用torch.device(f’cuda:{i}') 来表示第i块GPU(i从0开始)。
- 另外,cuda:0和cuda是等价的。
import torch
from torch import nn
torch.device('cpu')
torch.device('cuda')
torch.device('cuda:1')
查询可用gpu的数量。
torch.cuda.device_count()
在不存在所需所有GPU的情况下运行代码。
def try_gpu(i=0): #@save"""如果存在,则返回gpu(i),否则返回cpu()"""if torch.cuda.device_count() >= i + 1:return torch.device(f'cuda:{i}')return torch.device('cpu')def try_all_gpus(): #@save"""返回所有可用的GPU,如果没有GPU,则返回[cpu(),]"""devices = [torch.device(f'cuda:{i}')for i in range(torch.cuda.device_count())]return devices if devices else [torch.device('cpu')]
try_gpu()try_gpu(10)try_all_gpus()
5.6.2 张量与GPU
查询张量所在的设备。(默认情况下,张量是在CPU上创建的。)
x = torch.tensor([1, 2, 3])
x.device
# device(type='cpu')
- 需要注意的是,无论何时我们要对多个项进行操作,它们都必须在同一个设备上。
例如,如果我们对两个张量求和,我们需要确保两个张量都位于同一个设备上,否则框架将不知道在哪里存储结果,甚至不知道在哪里执行计算。
存储在GPU上
有几种方法可以在GPU上存储张量。例如,我们可以在创建张量时指定存储设备。
在第一个gpu上创建张量变量X。(在GPU上创建的张量只消耗这个GPU的显存。我们可以使用nvidia-smi命令查看显存使用情况。一般来说,需要确保不创建超过GPU显存限制的数据。)
X = torch.ones(2, 3, device=try_gpu())
X
# tensor([[1., 1., 1.],[1., 1., 1.]], device='cuda:0')
假设至少有两个GPU,下面的代码将在第二个GPU上创建一个随机张量。
Y = torch.rand(2, 3, device=try_gpu(1))
Y
# tensor([[0.4860, 0.1285, 0.0440],[0.9743, 0.4159, 0.9979]], device='cuda:1')
复制
如果我们要计算X + Y,我们需要决定在哪里执行这个操作。例如,如下图所示,不要简单地X加上Y,这会导致异常,运行时引擎不知道该怎么做:它在同一设备上找不到数据会导致失败。
由于Y位于第二个GPU上,所以我们需要将X移到那里,然后才能执行相加运算。

Z = X.cuda(1)
print(X)
print(Z)# tensor([[1., 1., 1.],[1., 1., 1.]], device='cuda:0')
# tensor([[1., 1., 1.],[1., 1., 1.]], device='cuda:1')
相关文章:

《动手学深度学习》学习笔记 第5章 深度学习计算
本系列为《动手学深度学习》学习笔记 书籍链接:动手学深度学习 笔记是从第四章开始,前面三章为基础知道,有需要的可以自己去看看 关于本系列笔记: 书里为了让读者更好的理解,有大篇幅的描述性的文字,内容很…...

【Redis】非关系型数据库之Redis的介绍及安装配置
目录 前言 一、关系型数据库与非关系型数据库 1.1关系型数据库 1.2非关系型数据库 1.3两者的区别 1.4非关系型数据库产生的背景 1.5总结 二、Redis介绍 2.1Redis是什么 2.2Redis的优点 2.3Redis的使用场景 2.4那些数据适合放在缓存中 2.5Redis为什么那么快…...

3D模型轻量化
在线工具推荐:3D数字孪生场景编辑器 - GLTF/GLB材质纹理编辑器 - 3D模型在线转换 - Three.js AI自动纹理开发包 - YOLO 虚幻合成数据生成器 - 三维模型预览图生成器 - 3D模型语义搜索引擎 近来,基于3D模型在影视作品、数字旅游项目诸多3D视觉领域都取得…...
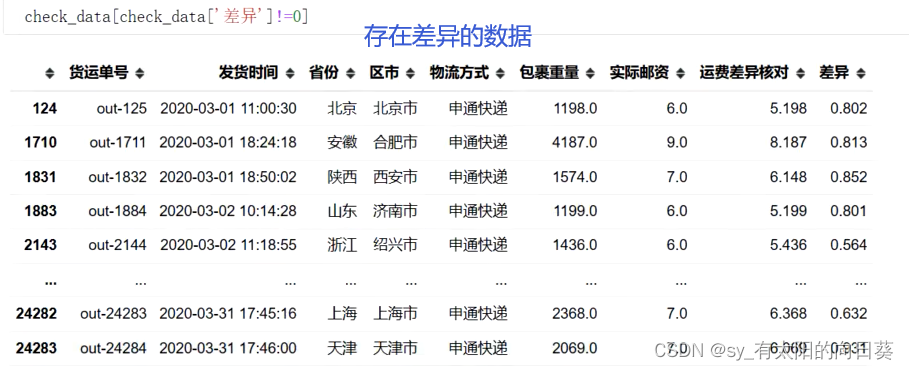
数据分析——快递电商
一、任务目标 1、任务 总体目的——对账 本项目解决同时使用多个快递发货,部分隔离区域出现不同程度涨价等情形下,如何快速准确核对账单的问题。 1、在订单表中新增一列【运费差异核对】来表示订单运费实际有多少差异,结果为数值。 2、将…...
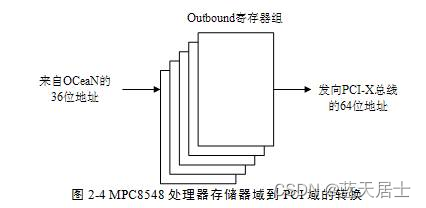
《PCI Express体系结构导读》随记 —— 第I篇 第2章 PCI总线的桥与配置(8)
接前一篇文章:《PCI Express体系结构导读》随记 —— 第I篇 第2章 PCI总线的桥与配置(7) 2.2 HOST主桥 MPC8548处理器的拓扑结构如图2-2所示: 2.2.2 存储器域地址空间到PCI总线域地址空间的转换 MPC8548处理器使用ATMUÿ…...
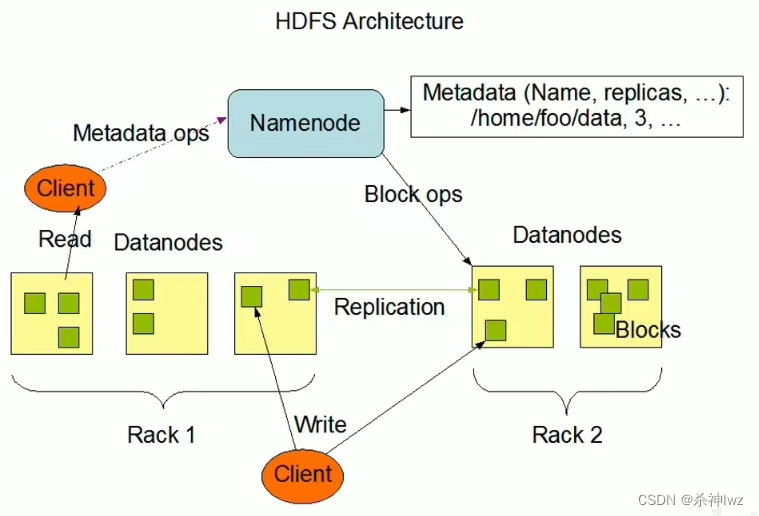
Hadoop分布式文件系统(二)
目录 一、Hadoop 1、文件系统 1.1、文件系统定义 1.2、传统常见的文件系统 1.3、文件系统中的重要概念 1.4、海量数据存储遇到的问题 1.5、分布式存储系统的核心属性及功能含义 2、HDFS 2.1、HDFS简介 2.2、HDFS设计目标 2.3、HDFS应用场景 2.4、HDFS重要特性 2.4…...
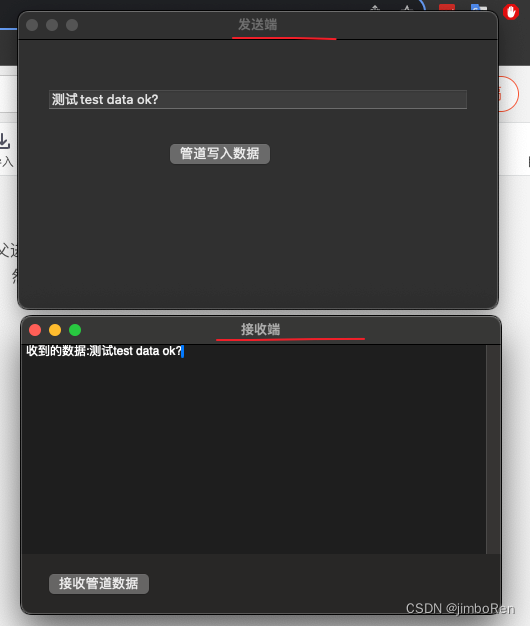
macOS跨进程通信: FIFO(有名管道) 创建实例
一: 简介 在类linux系统中管道分为有名管道和匿名管道。两者都能单方向的跨进程通信。 匿名管道(pipe): 必须是父子进程之间,而且子进程只能由父进程fork() 出来的,才能继承父进程的管道句柄,一般mac 开发…...
推荐几个免费的HTTP接口Mock网站和工具
在前后端分离开发架构下,经常遇到调用后端数据API接口进行测试、集成、联调等需求,比如: (1)前端开发人员很快开发完成了UI界面,但后端开发人员的API接口还没有完成,不能进行前后端数据接口对接…...

企业数据库安全管理规范
1.目的 为规范数据库系统安全使用活动,降低因使用不当而带来的安全风险,保障数据库系统及相关应用系统的安全,特制定本数据库安全管理规范。 2.适用范围 本规范中所定义的数据管理内容,特指存放在信息系统数据库中的数据。 本…...

react:ffcreator中FFCreatorCenter视频队例
最近项目要求,一键生成房子的推荐视频,选几张图,加上联系人的方式就是一个简单的视频,因为有web端、小程序端,为了多端口用,决定放在服务器端生成。 目前用的是react中的nextjs来开发项目。 nextjs中怎样…...
第434题字符串中的单词数(Python))
力扣(leetcode)第434题字符串中的单词数(Python)
434.字符串中的单词数 题目链接:434.字符串中的单词数 统计字符串中的单词个数,这里的单词指的是连续的不是空格的字符。 请注意,你可以假定字符串里不包括任何不可打印的字符。 示例: 输入: “Hello, my name is John” 输出: 5 解释: 这…...
django学习:页面渲染与请求和响应
1.请求过程 2.页面渲染 在app中新建一个目录(Directory),文件名命名为templates。该文件名命名是固定的,不可命名出错,如若后续步骤出错,该目录文件名是一个检查的重点项目。在该目录下新建一个html文件&a…...

Redis 数据一致性
概述 当我们在使用缓存时,如果发生数据变更,那么你需要同时操作缓存和数据库,而它们两个又分属不同的系统,因此无法做到同时操作成功或失败,因此在并发读写下很可能出现缓存与数据库数据不一致的情况 理论上可以通过…...
Mac环境下反编译apk
Mac环境下反编译apk 安装反编译工具dex2jar:[官网下载](https://sourceforge.net/projects/dex2jar/)JD-GUI:[官网下载](https://jd-gui.apponic.com/) 实操1. 将需要反编译的 .apk 文件放在下载的 dex2jar 文件夹目录下2. 使用 cd /xxx/dex2jar-2.0 命令…...

计算机网络——网络模型的组织、看法以及标准化流程
1. 通信技术和标准化领域中扮演重要角色的组织 1.1 国际和国家官方标准化机构 OSI:国际标准化组织(ISO),负责国际标准的制定,旨在确保全球产品和服务的安全性、可靠性和效率。它有许多国家分支机构,包括法…...

【JAVA】volatile 关键字的作用
🍎个人博客:个人主页 🏆个人专栏: JAVA ⛳️ 功不唐捐,玉汝于成 目录 前言 正文 volatile 的作用: 结语 我的其他博客 前言 在多线程编程中,保障数据的一致性和线程之间的可见性是…...
Next.js 第一次接触
因为需要整个漂亮的在线文档,所以接触了next.js,因为对前端js本身不够熟悉,别说对react.js 又不会,时间又不允许深入研究,所以,为了加一个导航菜单,极其痛苦。 有点小bug,不过不影响…...

CISSP 第7章:PKI和密码学应用
第七章 PKI和密码学应用 7.1 非对称密码学 对称密码系统具有共享的秘钥系统,从而产生了安全秘钥分发的问题 非对称密码学使用公钥和私钥对,无需支出复杂密码分发系统 7.1.1 公钥与私钥 7.1.2 RSA(兼具加密和数字签名) RSA算法依赖…...
ROS中创建dji_sdk节点包(二)实现代码)
dji uav建图导航系列()ROS中创建dji_sdk节点包(二)实现代码
在前文 【dji uav建图导航系列()ROS中创建dji_sdk节点包(一)项目结构】中简单介绍了项目的结构,和一些配置文件的代码。本文详细说明目录src下的节点源代码实现。 文章目录 1、代码结构2、PSDK部分3、ROS部分3.1、头文件3.1.1、外部调用 node_service.h3.1.2、节点类定义…...

数字化工厂产品推荐 带OPC UA的分布式IO模块
背景 近年来,为了提升在全球范围内的竞争力,制造企业希望自己工厂的机器之间协同性更强,自动化设备采集到的数据能够发挥更大的价值,越来越多的传统型工业制造企业开始加入数字化工厂建设的行列,实现智能制造。 数字化…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...
