当前位置：首页 > news >正文

K-means 聚类算法分析

news 2025/8/25 14:11:47

算法简述

K-means 算法原理

我们假定给定数据样本 X ，包含了 n 个对象 $X = \left \{ X_{1},X_{2},X_{3},...,X_{n}\right \}$ ，其中每一个对象都具有 m 个维度的属性。而 K-means 算法的目标就是将 n 个对象依据对象间的相似性聚集到指定的 k 个类簇中，每个对象属于且仅属于一个其到类簇中心距离最小的类簇中。对于 K-means 算法，首先需要初始化 k 个聚类中心 $\left \{ C_{1}, C_{2},C_{3},...,C_{k}, \right \},1<k\leq n$ , 然后通过计算每一个对象到每一个聚类中心的欧式距离，如下式所示：

$dis(X_{i},C_{i}) = \sqrt{\sum_{t=1}^{m} (X_{it}-C_{jt})^{2}}$

这里的 $X_{i}$ 表示第i个对象 $1<i<n$ ， $C_{i}$ 表示第 j 个聚类中心 $1<j<k$ ， $X_{it}$ 表示第i个对象的第t个属性， $1\leq t\leq m$ ， $C_{jt}$ 表示第j个聚类中心的第t个属性。

依次比较每一个对象到每一个聚类中心的距离，将对象分配到距离最近的聚类中心的类簇中，得到k个类簇 $\left \{S_{1},S_{2},S_{3},...,S_{k}\right \}$ ，kmeans 算法定义了类簇的原型，类簇中心就是类簇内所有对象在各个维度的均值，其计算公式如下所示：

$C_{t} = \frac{\sum_{X_{i}\in S_{i}}^{}X_{i}}{\left | S_{l} \right |}$

式中， $C_{l}$ 表示第l个聚类中心， $1\leq l\leq k$ ， $\left | S_{l} \right |$ 表示第l个类簇中对象的个数， $X_{i}$ 表示第l个类簇中第i个对象， $1\leq i\leq \left | S_{i} \right |$

算法实现流程

随机设置 K 个特征空间内的点作为初始的聚类中⼼。
对于其他每个点计算到 K 个中⼼的距离，未知的点选择最近的⼀个聚类中⼼点作为标记类别。
接着对着标记的聚类中⼼之后，重新计算出每个聚类的新中心点（平均值）
如果计算得出的新中⼼点与原中⼼点⼀样（质⼼不再移动），那么结束，否则重新进⾏第⼆步过程。

核心代码

手写实现 K-means 算法：

import numpy as np
import random
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
"""
手写实现Kmeans
"""
data = np.genfromtxt("classes.txt", delimiter='\t')
X = data
K = 5
colors = ['r', 'g', 'b', 'c', 'm', 'y', 'k']
max_iterations = 10000
random.seed(100)
def kmeans(data, K, max_iterations):initial_centers = random.sample(list(data), K)centers = initial_centersfor iteration in range(max_iterations):clusters = {i: [] for i in range(K)}for point in data:distances = [np.linalg.norm(point - center) for center in centers]cluster_index = np.argmin(distances)clusters[cluster_index].append(point)new_centers = [np.mean(clusters[i], axis=0) for i in range(K)]if np.all(np.array_equal(centers[i], new_centers[i]) for i in range(K)):breakcenters = new_centersreturn centers, clustersfinal_centers, final_clusters = kmeans(X, K, max_iterations)
for i in range(K):cluster = np.array(final_clusters[i])plt.scatter(cluster[:, 0], cluster[:, 1], c=colors[i], label=f'簇 {i + 1}')centers = np.array(final_centers)
plt.scatter(centers[:, 0], centers[:, 1], c='k', marker='x', s=100, label='簇中心')plt.xlabel('高度')
plt.ylabel('宽度')
plt.legend()
plt.show()

调用 sklearn 包的 K-means 算法：

import numpy as np
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
"""
调用sklearn库的Kmeans算法
"""
data = np.genfromtxt("classes.txt", delimiter='\t')
X = data
K = 3
num_experiments = 5
colors = ['r', 'g', 'b', 'c', 'm', 'y', 'k']
for i in range(num_experiments):kmeans = KMeans(n_clusters=K, init='k-means++', random_state=i)kmeans.fit(X)print(f"实验 {i + 1} - 初始中心: {kmeans.cluster_centers_}")kmeans = KMeans(n_clusters=K, init='k-means++', random_state=0)
kmeans.fit(X)labels = kmeans.labels_clustered_data = {i: [] for i in range(K)}
for i, label in enumerate(labels):clustered_data[label].append(X[i])for i in range(K):cluster = np.array(clustered_data[i])plt.scatter(cluster[:, 0], cluster[:, 1], c=colors[i], label=f'簇 {i + 1}')centers = kmeans.cluster_centers_
plt.scatter(centers[:, 0], centers[:, 1], c='k', marker='x', s=100, label='簇中心')plt.xlabel('高度')
plt.ylabel('宽度')
plt.legend()
plt.show()

手写实现 K-means 的算法流程：

随机选择 initial centers：从数据集中随机选择 K 个数据点，作为 initial centers。
计算距离：对于每个数据点，计算它与当前的 K 个 centers 之间的距离。
分配数据点：将每个数据点分配到最近的 center 所对应的集合中。
更新 centers：将每个集合的中心点更新为集合中的均值。
重复步骤 2-4：直到 centers 不再发生变化，或者达到最大迭代次数。
返回 centers 和 clusters：返回最终的 centers 和 clusters。

实验结果与分析

使用 python 手写实现 K-means 算法效果（假设 K=3 的时候）：

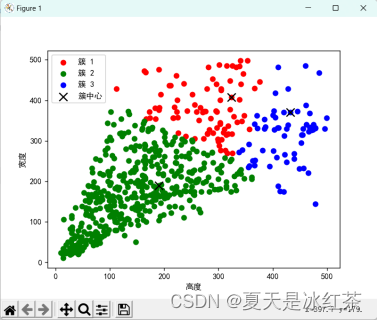
使用 sklearn 中的 K-means 算法效果（假设 K=3 的时候）：

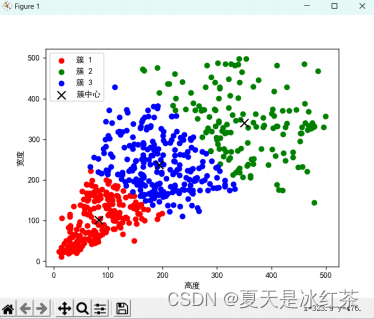
使用 python 手写实现 K-means 算法效果（假设 K=5 的时候）：

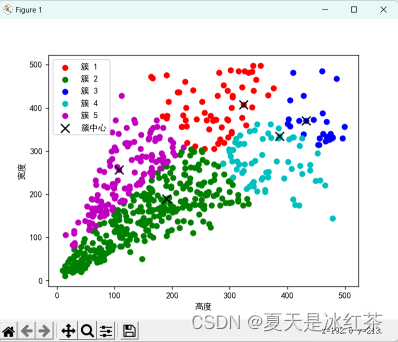
这里使用了 Python 手写实现 K-means 算法，并与 scikit-learn 库中的K-means 算法进行了比较。结果发现手写实现的 K-means 算法的效果与scikit-learn 库中的 K-means 算法相似，都可以很好地聚集数据点。

结论与心得体会

K-means 算法是一种常用的聚类算法，可以用来分组数据点 K 个聚类。在本实验中，我们使用了 VOC 数据集中的 600 张图像，并将每个图像的边界框标注为一个数据点。这里使用了 K-means 算法将这些数据点聚集到 K 个聚类中。

classes.txt文件：

K-means 聚类算法分析

算法简述

K-means 算法原理

算法实现流程

核心代码

实验结果与分析

结论与心得体会

相关文章：

K-means 聚类算法分析

uniapp获取定位

Python 面向对象之反射

HPM6750开发笔记《DMA接收和发送数据UART例程深度解析》

SQL IN 操作符

如何使用Plex在Windows系统搭建个人媒体站点公网可访问

web前端——clear可以清除浮动产生的影响

centos用yum安装mysql详细教程

冲刺2024年AMC8竞赛的专题突破：匹克定律和不规则形状面积的求法

阿里云迁移AWS视频点播技术攻坚

Scrum敏捷认证CSM官方认证班Certified ScrumMaster - CSM认证班

深度解析qt核心机制:信号槽的多线程行为与对象的线程依附性

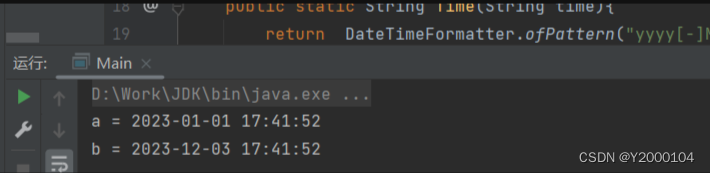
关于时间格式yyyy-M-d或yyyy-MM-d到yyyy-MM-dd的转换

【Windows】之微软输入法配置小鹤双拼

【AI】使用Jan.ai在本地部署大模型开启AI对话（含通过huggingface下载大模型，实现大模型自由）

C++摸版（初阶）----函数模版与类模版

Embedded-Project项目介绍

golang 的那些花样

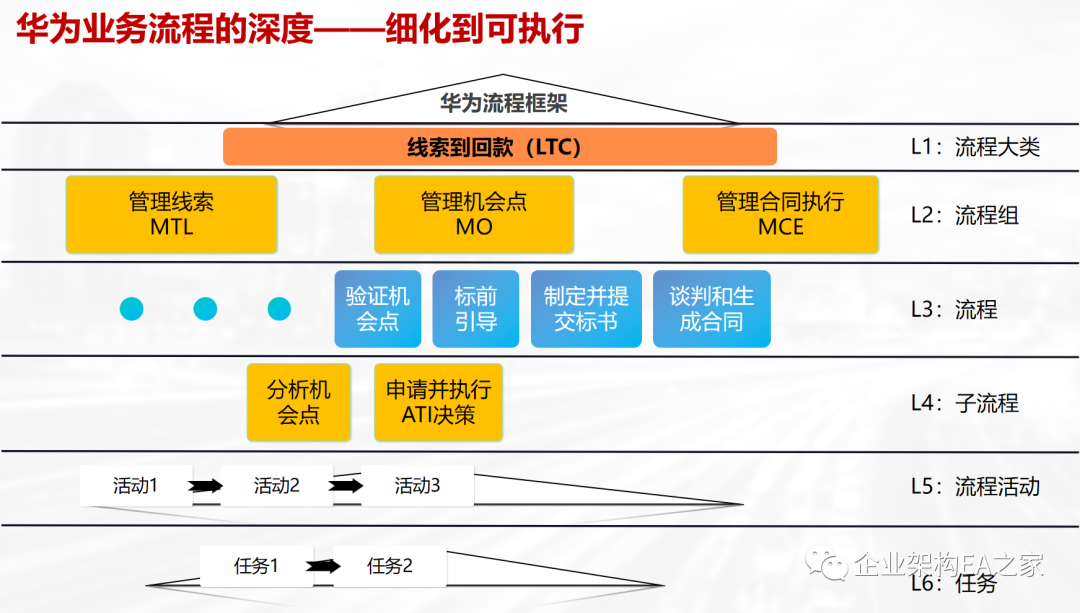
如何设计企业级业务流程？学习华为的流程六级分类经验

视频智能分析支持摄像头异常位移检测，监测摄像机异常位移变化，保障监控状态

基于算法竞赛的c++编程（28）结构体的进阶应用

stm32G473的flash模式是单bank还是双bank？

Opencv中的addweighted函数

微服务商城-商品微服务

BCS 2025｜百度副总裁陈洋：智能体在安全领域的应用实践

CMake控制VS2022项目文件分组

Hive 存储格式深度解析：从 TextFile 到 ORC，如何选对数据存储方案？

C++.OpenGL （14/64）多光源（Multiple Lights）

springboot整合VUE之在线教育管理系统简介

Java编程之桥接模式