Java十种经典排序算法详解与应用
数组的排序
前言
排序概念
排序是将一组数据,依据指定的顺序进行排列的过程。
排序是算法中的一部分,也叫排序算法。算法处理数据,而数据的处理最好是要找到他们的规律,这个规律中有很大一部分就是要进行排序,所以需要有排序算法。
常见的排序算法分类
排序分为:内部排序和外部排序。
- 内部排序:是将需要处理的所有数据加载到内存中进行排序;
- 外部排序:当数据量过大,无法全部加载到内存中,需要借助外部存储(文件、磁盘等)进行排序。
- 交换排序(冒泡排序、快速排序)
- 选择排序(选择排序、堆排序)
- 插入排序(插入排序、希尔排序)
- 归并排序
- 桶排序、 计数排序、基数排序
算法稳定性
假设在数列中存在a[i]=a[j],若在排序之前,a[i]在a[j]前面;并且排序之后,a[i]仍然在a[j]前面,则这个排序算法是稳定的。
如何分析算法
分析算法的执行效率
- 最好、最坏、平均情况时间复杂度。
- 时间复杂度的系数、常数和低阶。
- 比较次数,交换(或移动)次数。
分析排序算法的稳定性
概念:如果待排序的序列中存在值相等的元素,经过排序之后,相等元素之间原有的先后顺序不变。
稳定性重要性:可针对对象的多种属性进行有优先级的排序。
举例:给电商交易系统中的“订单”排序,按照金额大小对订单数据排序,对于相同金额的订单以下单时间早晚排序。用稳定排序算法可简洁地解决。先按照下单时间给订单排序,排序完成后用稳定排序算法按照订单金额重新排序。
分析排序算法的内存损耗
原地排序算法:特指空间复杂度是O(1)的排序算法。
冒泡排序
概念
冒泡排序是最基础的排序算法。属于交换排序算法。
冒泡排序重复地遍历要排序的数组元素,一次比较两个元素,如果他们的顺序错误就把他们交换过来。重复地进行直到没有再需要交换,也就是说该数组已经排序完成。
这个算法的名字由来是因为越大的元素会经过交换慢慢“浮”到数列的顶端,故名“冒泡排序”。
按照冒泡排序的思想,把相邻的元素两两比较,当一个元素大于右侧相邻元素时,交换它们的位置;当一个元素小于或等于右侧相邻元素时,位置不变。
冒泡排序只会操作相邻的两个数据。每次冒泡操作都会对相邻的两个元素进行比较,看是否满足大小关系要求,如果不满足就让它俩互换。
原理
- 比较相邻的元素。如果第一个比第二个大,就交换他们两个。
- 对每一对相邻元素做同样的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数。
- 针对所有的元素重复以上的步骤,除了最后一个。
- 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。

经过第一轮后: 元素9作为数列中最大的元素,就像是汽水里的小气泡一样,“漂”到了最右侧。
每一轮结束都会有一个元素被移到最右侧。

代码实现
public class Test01 {public static void main(String[] args) {int[] arr = {5, 8, 6, 3, 9, 2, 1, 7};for (int i = 0; i < arr.length-1; i++) {for (int j = 0; j < arr.length-1-i; j++) {if(arr[j] > arr[j+1]){//通过第三方变量实现两个变量的交换//缺点:需要声明变量//int temp = arr[j];//arr[j] = arr[j+1];//arr[j+1] = temp;//通过两个变量加减实现两个变量的交换//缺点:当两个变量相加超出int取值范围,会损失精度//arr[j] = arr[j] + arr[j+1] - (arr[j+1] = arr[j]);//通过位运算^异或实现两个变量的交换arr[j] = arr[j]^arr[j+1];arr[j+1] = arr[j]^arr[j+1];arr[j] = arr[j]^arr[j+1];}}}System.out.println(Arrays.toString(arr));}
}
口诀
N个数字来排队
两两相比小靠前
外层循环N-1
内层循环N-1-i
优化代码
为什么需要优化?
针对不同的数列,需要循环的轮数是有不同的。
例如:54321需要4轮循环之后才能排好序。而12345,当执行第一轮循环后,所有相邻的两个数值都无需换位,那说明排序正常,无需排序。不用执行后续的循环。


public class Test02 {public static void main(String[] args) {int[] arr = {5, 8, 6, 3, 9, 2, 1, 7};for (int i = 0; i < arr.length-1; i++) {//默认排好了boolean isSort = true;for (int j = 0; j < arr.length-1-i; j++) {if(arr[j] > arr[j+1]){isSort = false;arr[j] = arr[j]^arr[j+1];arr[j+1] = arr[j]^arr[j+1];arr[j] = arr[j]^arr[j+1];}}//排好了跳出循环if(isSort){break;}}System.out.println(Arrays.toString(arr));}
}
选择排序
概念
选择排序将数组分成已排序区间和未排序区间。初始已排序区间为空。每次从未排序区间中选出最小的元素放到已排序区间的末尾,直到未排序区间为空。
原理
选择排序是一种最简单的排序算法。其排序的逻辑如下:
- 有一个待排序的数组A
- 从A中找出最小的元素。
- 将找到的最小元素跟数组A中第一个元素交换位置(如果最小元素就是第一个元素,则自己跟自己交换位置)。如下图:

(如上图,长方形高低代表数字的大小,找到最小的数字,跟第一个位置的数据进行交换)
交换之后,结果如下图所示:

- 然后,在剩下的4个数字中再找到最小的那个数字,跟第2个位置的数字交换。如下图:

交换之后的结果如下如:
- 再在剩下的三个数字中,找到最小的那个数字跟第3个位置的数字交换位置。上图中剩下的三个数字中最小的就是第3个位置的数字,所以,它自己跟自己交换位置,就是不变。同理第 四个数字也是不变,第5个数字也是不变。(上图中例子第3、4、5个元素正好就是对应的排 序,所以不变。如果不是对应的最小数字,同理交换位置就行。) 以上就是选择排序的算法逻辑。
代码实现
public class Test01 {public static void main(String[] args) {int[] arr = {5, 8, 6, 3, 9, 2, 1, 7};for (int i = 0; i < arr.length; i++) {//最小值下标。初始默认假设第一个数字就是最小数字int minIndex = i;for (int j = i+1; j < arr.length; j++) {//如果找到更小的数字if(arr[minIndex] > arr[j]){//将minIndex变量的值修改为新的最小数字的下标minIndex = j;}}if(minIndex != i){arr[minIndex] = arr[minIndex] ^ arr[i];arr[i] = arr[minIndex] ^ arr[i];arr[minIndex] = arr[minIndex] ^ arr[i];}}System.out.println(Arrays.toString(arr));}
}
选择排序小结
选择排序是一种简单的排序算法,适用于数据量较小的情况,因为根据时间复杂度分析,数据量越大,选择排序所花费的时间按照平方倍数增长,会非常慢。
但是选择排序也有它的优势,选择排序的优势就是思维逻辑简单。
选择排序还有个特点,就是不论数组的顺序是排好序或者是乱序的,选择排序都需要花费一样的时间来计算。比如,利用选择排序对数组{1,2,3,4,5}和数组{3,1,4,2,5}排序所花费的时间是一样的。
插入排序
概念
插入排序将数组数据分成已排序区间和未排序区间(有序区间和无序区间)。
初始已排序区间只有一个元素,即数组第一个元素。从未排序区间取出一个元素插入到已排序区间,新插入的元素要与已排序区间的数据一一比较大小,直到该元素找到合适的位置。陆续从未排序区间取出数据插入到已排序区间,直到未排序区间为空。
实际操作过程中,未排序区间的第一个元素与已排序区间的最后一个元素比较大小,如果大于最后一个数据则不换位置,直接加到已排序区间的末尾。如果数据小于已排序区间的最后一个数据,则需要换位,并且该数据要与已排序区间前面的数据一一比较大小,直到找到合适的位置。
原理

有一个待排序的数组:5、2、4、6、1、3。插入排序步骤如下:
- 初始时,有序区间中只有5,无序区间中有2、4、6、1、3。
将无序区间的2插入到有序区间,先比较2和5的大小。2比5小则交换位置。
比较后,有序区间中是2、5,无序区间中有4、6、1、3。
- 再将4加入到有序区间,比较4和5的大小。4比5小,则交换位置。此时有序区间是2、4、5,顺序正确。
如果顺序不正确,4还要与2比较,必须保证有序区间一定是排好序的。此时无序区间中有6、1、3。
再将6加入到有序区间,比较6和5的大小。6比5大,则无需交换位置,直接将6放在有序区间的末尾。此时有序区间是2、4、5、6,此时无序区间中有1、3。
再将1加入到有序区间,比较1和6的大小。1比6小,则交换位置。1与6交换位置后,有序区间的顺序还是不正确,需要继续调整,1再与之前的数据一一比较,直到找到合适的位置。此时有序区间是1、2、4、5、6,此时无序区间中有3。
再将3加入到有序区间,比较3和6的大小。3比6小,则交换位置。3与6交换位置后,有序区间的顺序还是不正确,需要继续调整,3再与之前的数据一一比较,直到找到合适的位置。此时有序区间是1、2、3、4、5、6,此时无序区间有空。
当无序区间为空,也就意味着排序结束。最终排序结果为:1、2、3、4、5、6。
代码实现
public class Test01 {public static void main(String[] args) {int[] arr = {5, 2, 4, 6, 1, 3};for (int i = 0; i < arr.length; i++) {for (int j = i; j > 0; j--) {if(arr[j-1] > arr[j]){arr[j-1] = arr[j-1] ^ arr[j];arr[j] = arr[j-1] ^ arr[j];arr[j-1] = arr[j-1] ^ arr[j];}else{break;}}}System.out.println(Arrays.toString(arr));}
}
以上插入排序的java代码实现,代码中的第二个for循环是重点,第二个for循环是只比较当前数据左边的值,如果比左边的值小则交换位置,否则位置不变。
插入排序小结
插入排序适合如下类型的数组:
- 数组中的每一个元素距离其最终的位置都不远。比如{1,0,2,3,4,5},这个数组中0最终位置 应该是第一个位置,0此时的位置距离第一个位置不远。
- 一个有序的大数组中融入一个小数组。比如有序大数组{1,2,3,4,5,6},融入一个小数组 {0,1}。
- 数组中只有几个元素的位置不正确。 上述这三种情况的数组适合使用插入排序算法。打过麻将的同学可以想想,打麻将过程中不停地摸牌、打牌、整理牌的过程是不是就是一次插入排序呢! 排序是算法的基础,排序的用途很多。
快速排序
概念
快速排序(Quick Sort)是对冒泡排序的一种改进。由霍尔(C. A. R. Hoare)在1962年提出。
同冒泡排序一样,快速排序也属于交换排序算法,通过元素之间的比较和交换位置来达到排序的目的。
原理
通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
快速排序与冒泡排序不同的是,冒泡排序在每一轮中只把1个元素冒泡到数列的一端。而快速排序每次排序的时候设置一个基准点,将小于等于基准点的数全部放到基准点的左边,将大于等于基准点的数全部放到基准点的右边。这样每次交换的时候就不会像冒泡排序一样只能在相邻的数之间进行交换,交换的距离就得到提升。
快速排序之所比较快,因为相比冒泡排序,每次交换是跳跃式的。这样总的比较和交换次数就少了,速度自然就提高了。
快速排序在最坏的情况下,仍可能是相邻的两个数进行了交换。因此快速排序的最差时间复杂度和冒泡排序是一样的都是O(n²),它的平均时间复杂度为O(nlogn)。
快速排序这种思路就就是分治法。

步骤
快速排序一般基于递归实现。其步骤是这样的:
选定一个合适的值(理想情况中值最好,但实现中一般使用数组第一个值),称为“基准元素”(pivot)。
基于基准元素,将数组分为两部分,较小的分在左边,较大的分在右边。
第一轮下来,这个基准元素的位置一定在最终位置上。
对两个子数组分别重复上述过程,直到每个数组只有一个元素。
排序完成。
总结:快速排序,其实就是给基准元素找其正确索引位置的过程。
注意:快速排序算法有双边循环法和单边循环法
A.双边循环法
- 首先,选定基准元素pivot,并且设置两个指针left和right,指向数列的最左和最右两个元素。

从right指针开始,让指针所指向的元素和基准元素做比较。
right指向的数据如果小于pivot,则right指针停止移动,切换到left指针。否则right指针向左移动。
轮到left指针行动,让指针所指向的元素和基准元素做比较。
left指向的数据如果大于pivot,则left指针停止移动。否则left指针继续向右移动。
左右指针指向的元素交换位置。
right指针当前指向的数据1小于pivot,right指针停止,轮到left指针移动。
由于left开始指向的是基准元素,所以left右移1位。

left右移一位是7,由于7>4,所以left指针停下。这时left和right指针所指向的元素进行交换。

- 接下来重新切换到right指针,向左移动。right指针先移动到8,8>4,继续左移,指向到2。由于2<4,停止在2的位置。

第一轮下来数组为:3、1、2、4、5、6、8、7。本轮下来,本轮的基准元素4的位置就是最终排序完成应该放置的位置。
接下来,采用递归的方式分别对4之前的前半部分排序,再对4后面的后半部分排序。
代码实现
public class Test01 {public static void main(String[] args) {int[] arr = new int[]{4, 7, 6, 5, 3, 2, 8, 1};quickSort(arr, 0, arr.length-1);System.out.println(Arrays.toString(arr));}public static void quickSort(int[] arr, int startIndex, int endIndex){if(startIndex >= endIndex){return;}int pivotIndex = partition(arr, startIndex, endIndex);// 根据基准元素,分成两部分进行递归排序quickSort(arr, startIndex, pivotIndex-1);quickSort(arr, pivotIndex+1, endIndex);}public static int partition(int[] arr, int startIndex, int endIndex){// 取第1个位置(也可以选择随机位置)的元素作为基准元素int pivot = arr[startIndex];int left = startIndex;int right = endIndex;while(left != right){//控制right指针比较并左移while(left < right && arr[right] > pivot){right--;}//控制left指针比较并右移while (left < right && arr[left] <= pivot) {left++;}//交换left和right指针所指向的元素if(left < right){int temp = arr[left];arr[left] = arr[right];arr[right] = temp;}}//交换left和right指针所指向的元素arr[startIndex] = arr[left];arr[left] = pivot;return left;}
}
B.单边循环法
单边循环法只从数组的一边对元素进行遍历和交换。
- 开始和双边循环法相似,首先选定基准元素pivot。同时,设置一个mark指针指向数列起始位置, 这个mark指针代表小于基准元素的区域边界。

接下来,从基准元素的下一个位置开始遍历数组。
如果遍历到的元素大于基准元素,就继续往后遍历
如果遍历到的元素小于基准元素,则需要做两件事:
第一,把mark指针右移1位,因为小于pivot的区域边界增大了1;
第二,让最新遍历到的元素和mark指针所在位置的元素交换位置,因为最新遍历的元素归属于小 于pivot的区域
首先遍历到元素7,7>4,所以继续遍历。

接下来遍历到的元素是3,3<4,所以mark指针右移1位。

随后,让元素3和mark指针所在位置的元素交换,因为元素3归属于小于pivot的区域。

按照这个思路,继续遍历,后续步骤如图所示:

代码实现
public class Test01 {public static void main(String[] args) {//快速排序之单边循环法int[] arr = new int[]{4, 7, 3, 5, 6, 2, 8, 1};quickSort(arr, 0, arr.length-1);System.out.println(Arrays.toString(arr));}public static void quickSort(int[] arr, int startIndex, int endIndex){if(startIndex >= endIndex){return;}int pivotIndex = partition(arr, startIndex, endIndex);// 根据基准元素,分成两部分进行递归排序quickSort(arr, startIndex, pivotIndex-1);quickSort(arr, pivotIndex+1, endIndex);}public static int partition(int[] arr, int startIndex, int endIndex){// 取第1个位置(也可以选择随机位置)的元素作为基准元素int pivot = arr[startIndex];int mark = startIndex;for (int i = startIndex+1; i <= endIndex; i++) {if(pivot > arr[i]){mark++;int temp = arr[mark];arr[mark] = arr[i];arr[i] = temp;}}int temp = arr[startIndex];arr[startIndex] = arr[mark];arr[mark] = temp;return mark;}
}
希尔排序
概念
希尔排序(Shell’s Sort)是插入排序的一种,又称“缩小增量排序”(Diminishing Increment Sort),是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因 D.L.Shell 于 1959 年提出而得名。
希尔排序是基于插入排序的以下两点性质而提出改进方法的:
插入排序本身还不够高效,插入排序每次只能将数据移动一位。当有大量数据需要排序时,会需要大量的移位操作。
但是插入排序在对几乎已经排好序的数据操作时,效率很高,几乎可以达到线性排序的效率。
所以,如果能对数据进行初步排列后,再用插入排序,那么就会大大提高效率。
希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;当增量减至 1 时,整个文件恰被分成一组,算法便终止。
由于多次插入排序,我们知道一次插入排序是稳定的,不会改变相同元素的相对顺序,但在不同的插入排序过程中,相同的元素可能在各自的插入排序中移动,最后其稳定性就会被打乱,所以shell排序是不稳定的。
原理
把元素按步长gap分组,对每组元素采用直接插入排序方法进行排序;
随着步长逐渐减小,所分成的组包含的元素越来越多;
当步长值减小到1时,整个数据合成一组,构成一组有序记录,完成排序;

代码实现
public class Test01 {public static void main(String[] args) {int[] arr = new int[]{9, 1, 2, 5, 7, 4, 8, 6, 3, 5};for (int gap = arr.length/2; gap > 0; gap/=2) {for (int i = gap; i < arr.length; i++) {for (int j = i-gap; j >= 0; j-= gap) {System.out.println(j + " -- " + (j+gap));if(arr[j] > arr[j+gap]){arr[j] = arr[j]^arr[j+gap];arr[j+gap] = arr[j]^arr[j+gap];arr[j] = arr[j]^arr[j+gap];}}System.out.println("xxxxx");}System.out.println("yyyy");}System.out.println(Arrays.toString(arr));}
}
希尔排序优劣
优点:算法较简单,代码短,需要的空间小,速度还可以,适合中小规模的排序。
缺点:速度偏慢,不够智能,不适合情况简单的排序,不适合大规模排序。
希尔排序稳定性
希尔排序是不稳定的算法,它满足稳定算法的定义。对于相同的两个数,可能由于分在不同的组中而导致它们的顺序发生变化。
算法稳定性 – 假设在数列中存在a[i]=a[j],若在排序之前,a[i]在a[j]前面;并且排序之后,a[i]仍然在a[j]前面。则这个排序算法是稳定的!
归并排序
概念
归并排序是一类与插入排序、交换排序、选择排序不同的另一种排序方法。
归并排序是采用分治法的一个非常典型的应用。归并排序的思想就是先递归分解数组,再合并数组。
将数组分解最小之后,然后合并两个有序数组,基本思路是比较两个数组的最前面的数,谁小就先取谁,取了后相应的指针就往后移一位。然后再比较,直至一个数组为空,最后把另一个数组的剩余部分复制过来即可。
归并排序有多路归并排序、两路归并排序 , 可用于内排序,也可以用于外排序。
原理
分而治之(divide - conquer)。
每个递归过程涉及三个步骤:
第一, 分解: 把待排序的 n 个元素的序列分解成两个子序列, 每个子序列包括 n/2 个元素;
第二, 治理: 对每个子序列分别调用归并排序MergeSort,进行递归操作;
第三, 合并: 合并两个排好序的子序列,生成排序结果。

代码实现
public class Test01 {public static void main(String[] args) {int[] arr = new int[]{4, 7, 3, 5, 6, 2, 8, 1};mergeSort(arr, 0, arr.length-1);System.out.println(Arrays.toString(arr));}public static void mergeSort(int[] arr, int low, int high) {if(low < high){int mid = (low+high)/2;mergeSort(arr, low, mid);mergeSort(arr, mid+1, high);// 左右归并merge(arr, low, mid, high);}}public static void merge(int[] arr, int low, int mid, int high) {int[] temp = new int[high-low+1];int i = low;int j = mid+1;int k = 0;// 把较小的数先移到新数组中while(i<=mid && j<=high){if(arr[i]<arr[j]){temp[k++] = arr[i++];}else{temp[k++] = arr[j++];}}// 把左边剩余的数移入数组while(i <= mid){temp[k++] = arr[i++];}// 把右边边剩余的数移入数组while(j <= high){temp[k++] = arr[j++];}// 把新数组中的元素覆盖arr数组for (int x = 0; x < temp.length; x++) {arr[x+low] = temp[x];}}
}
桶排序
概念
桶排序,顾名思义会用到“桶" 。核心思想是将要排序的数据分到几个有序的桶里,每个桶里的数据单独进行排序。桶内排完序之后,再把每个桶里的数据按照顺序依次取出,组成的序列就是有序的了。
桶排序同样是一种线性时间的排序算法。桶排序需要创建若干个桶来协助排序,每一个桶(bucket)代表一个区间范围,里面可以承载一个或多个元素。
除了对一个桶内的元素做链表存储,也有可能对每个桶中的元素继续使用其他排序算法进行排序,所以更多时候,桶排序会结合其他排序算法一起使用。
桶排序对排序的数据要求苛刻:
- 要排序的数据需要很容易就能划分成m个桶,并且桶与桶之间有着天然的大小顺序;
- 数据在各个桶之间的分布是比较均匀的;
- 桶排序比较适合用在外部排序中。
所谓的外部排序就是数据存储在外部磁盘中,数据量比较大,内存有限,无法将数据全部加载到内存中。
原理
- 桶排序的第1步,就是创建这些桶,并确定每一个桶的区间范围具体需要建立多少个桶,如何确定桶的区间范围,有很多种不同的方式。我们这里创建的桶数量等于原始数列的元素数量,除最后一个桶只包含数列最大值外, 前面各个桶的区间按照比例来确定。
区间跨度 = (最大值-最小值)/ (桶的数量 - 1)
假设有一个非整数数列如下:4.5、0.84、3.25、2.18、0.5
桶的个数为5,计算出区间跨度为1。
序列:4.5、0.84、3.25、2.18、0.5
区间跨度 = (最大值-最小值)/(桶的数量-1)
区间跨度 = 1.0
0.5-1.5 (0号桶中:0.84, 0.5)
1.5-2.5 (1号桶中:2.18)
2.5-3.5 (2号桶中:3.25)
3.5-4.5 (3号桶中:空)
4.5-5.5 (4号桶中:4.5)
如何计算当前数据属于某个区间,或者说在哪个桶里?
桶编号 = (int) ((元素数值 - 最小值) / 区间跨度);

- 遍历原始数列,把元素对号入座放入各个桶中。

- 对每个桶内部的元素分别进行排序(显然,只有第1个桶需要排序)

- 遍历所有的桶,输出所有元素 :0.5、0.84、2.18、3.25、4.5
代码实现
public class Test01 {public static void main(String[] args) {//桶排序double[] arr = new double[]{4.5, 0.84, 3.25, 2.18, 0.5};bucketSort(arr);System.out.println(Arrays.toString(arr));}public static void bucketSort(double[] arr){// 获取最大值和最小值double max = arr[0];double min = arr[0];for (int i = 1; i < arr.length; i++) {if(max < arr[i]){max = arr[i];}if(min > arr[i]){min = arr[i];}}// 获取桶个数int bucketCount = arr.length;// 计算区间跨度 = (最大值-最小值)/(桶的数量-1)double span = (max-min)/(bucketCount-1);// 桶的初始化ArrayList<LinkedList<Double>> list = new ArrayList<>(bucketCount);for (int i = 0; i < bucketCount; i++) {list.add(new LinkedList<>());}// 循环获取元素应该放在哪个区间内,也就是获取桶的编号for (int i = 0; i < arr.length; i++) {// 获取当前数据应该放在哪个区间内,也就是获取桶的编号int num = (int) ((arr[i]-min)/span);list.get(num).add(arr[i]);}// 对每个桶内部进行排序for (LinkedList<Double> linkedList : list) {Collections.sort(linkedList);}// 将数据回填到原数组中int index = 0;for (LinkedList<Double> linkedList : list) {for (Double element : linkedList) {arr[index++] = element;}}}
}
基数排序
概念
基数排序是桶排序的扩展。是1887年赫尔曼.何乐礼发明的。基数排序的基本实现原理是:将整数按位切割成不同的数字,然后按位数进行比较。
基数排序是经典的空间换时间的算法。占用内存很大,当对海量数据排序时,容易造成OutOfMemoryError。
原理
- 有一串数值如下所示:64, 32, 90,76, 11,93, 85, 44, 18, 21, 65, 89, 57,11
首先根据个位数的数值,将它们分配至编号0到9的桶子中:

- 将这些桶子中的数值重新串接起来,成为的数列为:90, 11, 21, 11, 32, 93, 64, 44, 85, 65, 76, 57, 18, 89
接着再进行一次分配,这次是根据十位数来分配:

- 将这些桶子中的数值重新串接起来,成为的数列为:11, 11, 18, 21, 32, 44, 57, 64, 65, 76, 85, 89, 90, 93
这时候整个数列已经排序完毕。
如果排序的对象有三位数以上,则持续进行以上的动作直至最高位数为止。
代码实现
基数排序的实现,有两种方式。
低位优先法,适用于位数较小的数排序,简称LSD。
高位优先法,适用于位数较多的情况,简称MSD。
LSD的基数排序适用于位数小的数列,如果位数多的话,使用MSD的效率会比较好。
MSD的方式与LSD相反,是由高位数为基底开始进行分配,但在分配之后并不马上合并回一个数组中,而是在每个“桶子”中建立“子桶”,将每个桶子中的数值按照下一数位的值分配到“子桶”中。在进行完最低位数的分配后再合并回单一的数组中。
public class Test01 {public static void main(String[] args) {//基数排序int[] arr = {64, 32, 90,76, 11,93, 85, 44, 18, 21, 65, 89, 57, 11};radixSort(arr);System.out.println(Arrays.toString(arr));}public static void radixSort(int[] arr){//获取最大值int max = arr[0];for (int i = 1; i < arr.length; i++) {if(max < arr[i]){max = arr[i];}}//获取最大值的位数(目的:用来判断需要进行几轮基数排序)int maxLen = String.valueOf(max).length();//定义10个桶容器。// 数组的第一维表示0-9,二维下标按照最大可能arr.length来计算。int[][] bucket = new int[10][arr.length];//创建桶计数器// 记录每个桶中放置数据的个数。数组元素共10个,表示10个桶。// 数组索引表示桶的编号,索引对应的数值是该桶中的数据个数int[] elementCount = new int[10];//times是记录重复操作轮数的计数器。重复次数取决了最大数值的位数//循环中定义变量n,用来表示位数。1表示个位,10表示十位,100表示百位。目的是获取数字每个位上的值。for (int times= 1, n = 1; times<= maxLen; times++,n*=10) {// 遍历数值,放到桶中for (int i = 0; i < arr.length; i++) {//获取元素个位、十位、百位上的数字。就是桶编号int lsd = arr[i]/n%10;//将数值放入桶中bucket[lsd][elementCount[lsd]] = arr[i];//桶计数器增加elementCount[lsd]++;}//数组索引下标。每轮结束都要形成新的数列,数组下标重新记录。int index = 0;// 从10个桶中取出数据,形成新的数列for (int i = 0; i < bucket.length; i++) {//判断桶中是否有数据if(elementCount[i] > 0){for (int j = 0; j < elementCount[i]; j++) {arr[index++] = bucket[i][j]; }}//遍历完数据,将计数器清空,下次重新计数elementCount[i] = 0;}}}
}
计数排序
概念
计数排序,这种排序算法是利用数组下标来确定元素的正确位置的。
计数排序是基本的桶排序。
定义n个桶,每个桶一个编号,数据放到相应编号的桶中。定义一个数组,数组索引表示桶的编号,索引值就是存放的数值。如果该值为1说明只出现一次,如果大于1,说明重复多次出现。
计数排序是典型的空间换时间的算法。
原理
- 假设数组中有10个整数,取值范围为0~10,要求用最快的速度把这10个整数从小到大进行排序。 可以根据这有限的范围,建立一个长度为10的数组。数组下标从0到9,元素初始值全为0。

假设数组数据为:7 3 2 1 9 6 5 4 3 8
下面就开始遍历这个无序的随机数列,每一个整数按照其值对号入座,同时,对应数组下标的元素进行加1操作。
最终,当数列遍历完毕时,数组的状态如下:

该数组中每一个下标位置所对应的值,其实就是数列中对应整数出现的次数。
直接遍历数组,输出数组元素的下标值,元素的值就是输出的次数。0不输出。
输出: 1 2 3 3 4 5 6 7 8 9
- 如果起始数不是从0开始,比如以下数列:
95,94,91,98,99,90,99,93,91,92,数组起始数为90。就采用偏移量的方式来排序。

数组遍历完毕,数组的状态如下:

原本输出:0 1 1 2 3 4 5 8 9 9
增加上偏移量90后,实际应该顺序输出为:90 91 91 92 93 94 95 98 99 99
代码实现
public class Test01 {public static void main(String[] args) {//计数排序int[] arr = makeRandomArr(50, 60, 100);System.out.println(Arrays.toString(arr));countSort(arr);System.out.println(Arrays.toString(arr));}public static void countSort(int[] arr){// 获取最大值和最小值int max = arr[0];int min = arr[0];for (int i = 0; i < arr.length; i++) {if(max < arr[i]){max = arr[i];}if(min > arr[i]){min = arr[i];}}// 计算桶的数量int bucketNum = max-min+1;//创建桶数组int[] buckets = new int[bucketNum];//遍历原数组for (int i = 0; i < arr.length; i++) {//计算元素在桶中的编号int n = arr[i]-min;//桶上计数累加++buckets[n];}// 将数据回填到原数组中int index = 0;for (int i = 0; i < buckets.length; i++) {if(buckets[i] > 0){for (int j = 0; j < buckets[i]; j++) {// 实际数值 = 桶编号 + 最小数值arr[index++] = i + min;}}}}/*** 全班50个人,最低成绩60分,最高成绩100分。将这些成绩进行排序。* 随机生成50个成绩。*/public static int[] makeRandomArr(int count,int min,int max){int[] arr = new int[count];Random ran = new Random();for (int i = 0; i < arr.length; i++) {int element = ran.nextInt(max-min)+min;arr[i] = element;}return arr;}
}
堆排序
概念
堆是具有以下性质的完全二叉树
大顶堆:每个节点的值都大于或等于其左右孩子节点的值**。**

小顶堆:每个结点的值都小于或等于其左右孩子结点的值。

对堆中的结点按层进行编号,将这种逻辑结构映射到数组中:

该数组从逻辑上讲就是一个堆结构,用简单的公式来描述一下堆的定义就是:
大顶堆:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
小顶堆:arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]
原理
将待排序序列构造成一个大顶堆,此时,整个序列的最大值就是堆顶的根节点。 将其与末尾元素进行交换,此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆,这样会得 到n个元素的次小值。如此反复执行,便能得到一个有序序列了。
- 构造初始堆
将给定无序序列构造成一个大顶堆(一般升序采用大顶堆,降序采用小顶堆)。

- 此时从最后一个非叶子节点开始(叶子节点自然不用调整,第一个非叶子节点 arr.length/2- 1=5/2-1=1,也就是下面的6结点),从左至右,从下至上进行调整。

- 找到第二个非叶节点4,由于[4,9,8]中9元素最大,4和9交换

- 这时,交换导致了子根[4,5,6]结构混乱,继续调整,[4,5,6]中6最大,交换4和6。

此时,我们就将一个无序序列构造成了一个大顶堆。
- 将堆顶元素与末尾元素进行交换,使末尾元素最大。然后继续调整堆,再将堆顶元素与末尾元素交换,得到第二大元素。如此反复进行交换、重建、交换。将堆顶元素9和末尾元素4进行交换

重新调整结构,使其继续满足大顶堆

再将堆顶元素8与末尾元素5进行交换,得到第二大元素8

继续进行调整成大顶堆,顶部的6与右子树的4交换,最终使得整个序列有序。
代码实现
public class Test01 {public static void main(String[] args) {//堆排序int[] arr = {4, 6, 8, 5, 9};heapSort(arr);System.out.println(Arrays.toString(arr));}public static void heapSort(int[] arr){//构建堆for (int i = arr.length/2-1; i >= 0; i--) {adjustHeap(arr, i, arr.length);}for (int i = arr.length-1; i > 0; i--) {//堆顶与末尾元素调换arr[0] = arr[0]^arr[i];arr[i] = arr[0]^arr[i];arr[0] = arr[0]^arr[i];//将堆顶元素下沉(目的:是将最大元素上浮到堆顶)adjustHeap(arr, 0, i);}}public static void adjustHeap(int[] arr,int index,int length){int leftChild = index+1;//左边节点下标int rightChild = index+2;//右边节点下标int parentIndex = index;//父节点下标//下沉左边if(leftChild < length && arr[parentIndex] < arr[leftChild]){parentIndex = leftChild;}//下沉右边if(rightChild < length && arr[parentIndex] < arr[rightChild]){parentIndex = rightChild;}if(index != parentIndex){arr[index] = arr[index] ^ arr[parentIndex];arr[parentIndex] = arr[index] ^ arr[parentIndex];arr[index] = arr[index] ^ arr[parentIndex];//继续下沉adjustHeap(arr, parentIndex, length);}}
}
Arrays.sort()
概念
Arrays.sort排序算法是双基准元素快速排序DualPivotQuicksort。
由弗拉基米尔·雅罗斯拉夫斯基Vladimir Yaroslavskiy,乔恩·本特利Jon Bentley和约书亚·布洛克Josh Bloch提供该算法。
在许多数据集上表现出O(nlogn)的时间复杂度,比传统的(单基准元素)快速排序算法性能更快。
原理
- 在微小数组上使用插入排序(Use insertion sort on tiny arrays)
int INSERTION_SORT_THRESHOLD = 47;
如果要排序的数组长度小于INSERTION_SORT_THRESHOLD这个常量,则插入排序优先于快速排序。
- 对小数组使用快速排序(Use Quicksort on small arrays)
int QUICKSORT_THRESHOLD = 286;
如果要排序的数组长度小于QUICKSORT_THRESHOLD这个常量,则快速排序优先于归并排序。
- 数组接近排序,使用归并排序(Check if the array is nearly sorted)
int MAX_RUN_COUNT = 67; //归并排序的最大运行次数。
int MAX_RUN_LENGTH = 33; //归并排序运行的最大长度。
数组不是高度结构化的,使用快速排序代替归并排序。
- 对大数组使用计数排序(Use counting sort on large arrays)
int COUNTING_SORT_THRESHOLD_FOR_BYTE = 29;
如果要排序的字节数组的长度大于COUNTING_SORT_THRESHOLD_FOR_BYTE该常量,则优先使用计数排序而不是插入排序。
- 对大数组使用计数排序(Use counting sort on large arrays)
int COUNTING_SORT_THRESHOLD_FOR_SHORT_OR_CHAR = 3200;
如果要排序的短数组或char数组的长度大于COUNTING_SORT_THRESHOLD_FOR_SHORT_OR_CHAR该常量,则优先使用计数排序而不是快速排序。
源码截图
- 在微小数组上使用插入排序(Use insertion sort on tiny arrays)

- 对小数组使用快速排序(Use Quicksort on small arrays)

- 数组接近排序,使用归并排序(Check if the array is nearly sorted)

- 对大数组使用计数排序(Use counting sort on large arrays)

- 对大数组使用计数排序(Use counting sort on large arrays)

排序算法与复杂度归类
注:学习完时间复杂度和空间复杂度的内容再做一下学习
- 根据时间复杂度的不同,主流的排序算法可以分为3大类:
时间复杂度为O(n²)的排序算法:冒泡排序、选择排序、插入排序(冒选插)
时间复杂度为O(nlogn)的排序算法: 快速排序 、堆排序、希尔排序、归并排序 (快堆希归)
时间复杂度为线性O(n)的排序算法:桶排序、 计数排序、基数排序(桶计基)
各个排序算法比对表:
| 排序算法 | 时间复杂度 | 空间复杂度 | 是否稳定 | 比较次数 |
|---|---|---|---|---|
| 冒泡排序 | 平均、最差:O(n²) | O(1) | 稳定 | 未优化无序/有序:(n-1)² 优化有序:n-1 优化最差:n(n-1)/2 |
| 选择排序 | 平均、最差:O(n²) | O(1) | 不稳定 | 无序/有序固定:n(n-1)/2 |
| 插入排序 | 平均、最差:O(n²) | O(1) | 稳定 | 有序:n-1 无序最差:n(n-1)/2 |
| 快速排序 | 平均、最差:O(nlogn) | O(nlogn) | 不稳定 | 属于交换排序 |
| 堆排序 | 平均、最差:O(nlogn) | O(1) | 不稳定 | 属于选择排序 |
| 希尔排序 | 平均:O(n^1.5) 最好:O(nlogn) | O(1) | 不稳定 | (n-1)^1.5 nlogn |
| 归并排序 | 平均、最差:O(nlogn) | O(n) | 稳定 | |
| 桶排序 | O(n) | O(n) | 稳定 | 适用于浮点数,适用于外部排序 |
| 计数排序 | O(m+n) | O(m) 0-10 m=10? | 稳定 | 适合于连续的取值范围不大的数组 |
| 基数排序 | 平均、最差:O(d*n) d为位数 | O(n) | 稳定 | 处理海量数据排序时容易OutOfMemoryError |
- 各种排序算法性能对比
执行1万个随机数的排序,同一台机器相同条件下的测试结果:
冒泡145ms、选择95ms、插入46ms
快速2ms、堆2ms、希尔5ms、归并3ms
计数1ms、基数2ms、桶17ms
Arrays.sort:4ms
Collections.sort:10ms
执行5万个随机数的排序,同一台机器相同条件下的测试结果:
冒泡4267ms、选择2282ms、插入1036ms
快速9ms、堆9ms、希尔12ms、归并14ms
计数3ms、基数7ms、桶38ms
Arrays.sort:11ms
Collections.sort:24ms
执行10万个随机数的排序,同一台机器相同条件下的测试结果:
冒泡16406ms、选择8633ms、插入4067ms
快速16ms、堆16ms、希尔19ms、归并21ms
计数6ms、基数11ms、桶49ms
Arrays.sort:19ms
Collections.sort:47ms
排序效率排名:计数、基数 、快速、堆、希尔、归并、桶、插入、选择、冒泡
- 根据其稳定性,可以分为稳定排序和不稳定排序
稳定排序:值相同的元素在排序后仍然保持着排序前的顺序
不稳定排序:值相同的元素在排序后打乱了排序前的顺序。(选择、快速、堆、希尔)
相关文章:

Java十种经典排序算法详解与应用
数组的排序 前言 排序概念 排序是将一组数据,依据指定的顺序进行排列的过程。 排序是算法中的一部分,也叫排序算法。算法处理数据,而数据的处理最好是要找到他们的规律,这个规律中有很大一部分就是要进行排序,所以需…...

git常用命令及概念对比
查看日志 git config --list 查看git的配置 git status 查看暂存区和工作区的变化内容(查看工作区和暂存区有哪些修改) git log 查看当前分支的commit 记录 git log -p commitID详细查看commitID的具体内容 git log -L :funcName:fileName 查看file…...

57、python 环境搭建[for 计算机视觉从入门到调优项目]
从本节开始,进入到代码实战部分,在开始之前,先简单进行一下说明。 代码实战部分,我会默认大家有一定的编程基础,不需要对编程很精通,但是至少要会 python 的基础语法、python 环境搭建、pip 的使用;C++ 要熟悉基础知识和基础语法,会根据文章中的步骤完成 C++ 的环境搭…...
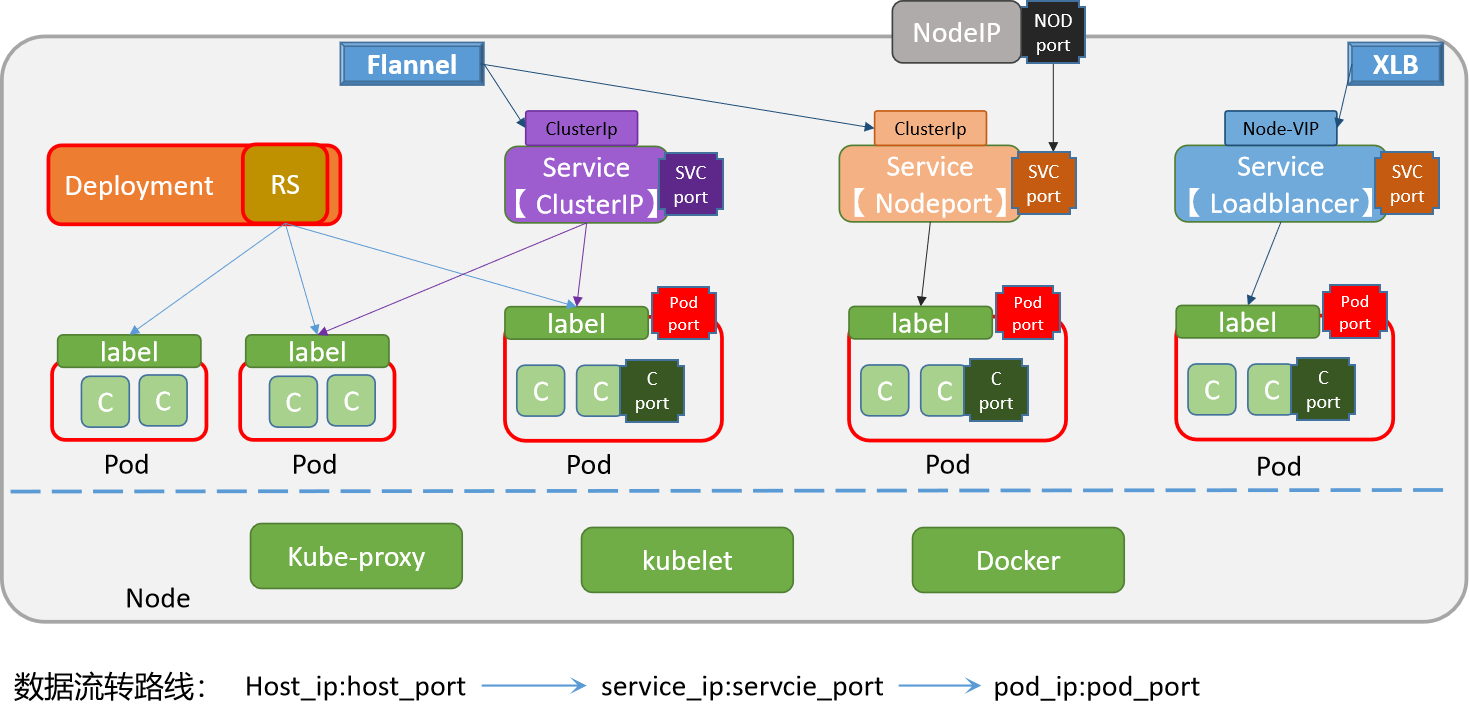
K8S-应用访问
1 service对象定位 2 Service 实践 手工创建Service 根据应用部署资源对象,创建SVC对象 kubectl expose deployment nginx --port80 --typeNodePortyaml方式创建Service nginx-web的service资源清单文件 apiVersion: v1 kind: Service metadata:name: sswang-ngi…...
商智C店H5性能优化实战
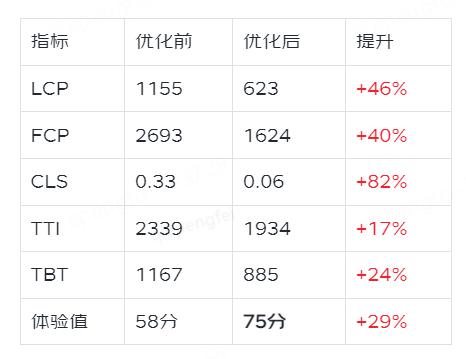
前言 商智C店,是依托移动低码能力搭建的一个应用,产品面向B端商家。随着应用体量持续增大,考虑产品定位及用户体验,我们针对性能较差页面做了一次优化,并取得了不错的效果,用户体验值(UEI&…...

Unity 使用 Plastic 同步后,正常工程出现错误
class Newtonsoft.Json.Linq.JToken e CS0433:类型"JToken"同时存在于"Newtonsoft.Json.Net20,Version3.5.0.0,Cultureneutral,,PublicKeyToken30ad4fe6b2a6aeed"和"Newtonsoft.Json, Version12.0.0.0,Cultureneutral,PublicKeyToken30ad4fe6b2a6aeed…...

详细设计文档该怎么写
详细设计文档是软件开发过程中的一个关键阶段,它为每个软件模块的实现提供了详细说明。这份文档通常在概要设计阶段之后编写,目的是指导开发人员如何具体实现软件的功能。以下是撰写详细设计文档的步骤和一些示例: 步骤和组成部分 引言 目的…...
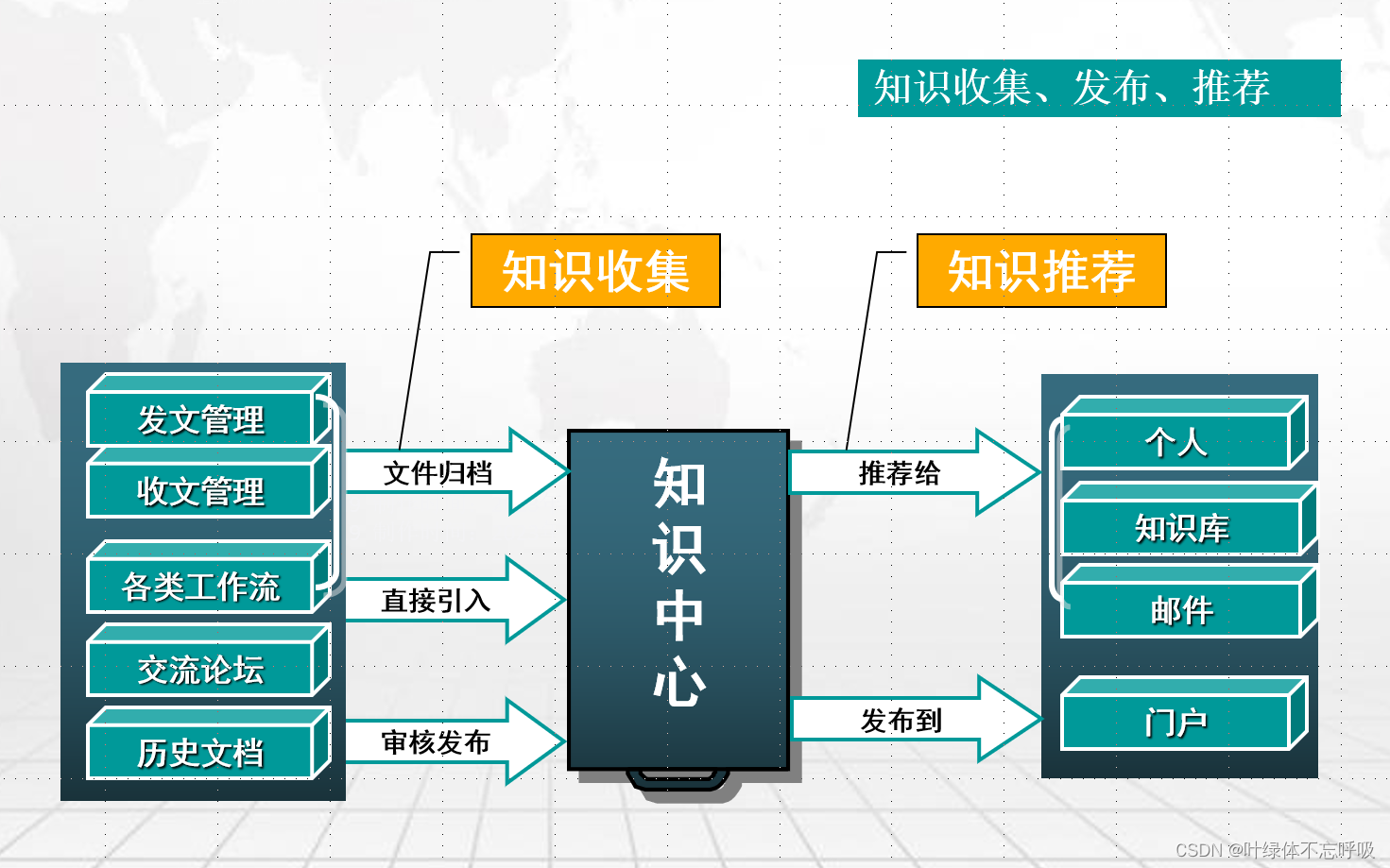
集团企业OA办公协同平台建设方案
一、企业对协同应用的需求分析 实现OA最核心、最基础的应用 业务流转:收/发文、汇报、合同等各种审批事项的业务协作与办理 信息共享:规章制度、业务资料、共享信息资源集中存储、统一管理 沟通管理:电子邮件、手机短信、通讯录、会议协作等…...

Spring Security之认证
系列文章目录 提示:这里可以添加系列文章的所有文章的目录,目录需要自己手动添加 Spring Security之认证 提示:写完文章后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 系列文章目录前言一、什么是Spring…...

智能语音机器人NXCallbot
受出海公司业务全球化的影响,智能客服逐渐从便捷应用变为市场刚需。新基建七大领域中,人工智能及场景应用的基础建设是最核心的领域,而智能客服作为商业化实际应用的核心场景之一,能提升企业运营效率,为行业客户赋能。…...

Vue 3中toRaw和markRaw的使用
Vue 3的响应性系统 在Vue 3中,响应性系统是构建动态Web应用程序的关键部分。Vue使用响应性系统来跟踪依赖关系,使数据更改能够自动更新视图。这使得Vue应用程序在数据变化时能够高效地更新DOM。Vue 3引入了新的Proxy对象来替代Vue 2中的Object.definePro…...

移动神器RAX3000M路由器不刷固件变身家庭云之三:外网访问家庭云
本系列文章: 移动神器RAX3000M路由器变身家庭云之一:开通SSH,安装新软件包 移动神器RAX3000M路由器变身家庭云之二:安装vsftpd 移动神器RAX3000M路由器变身家庭云之三:外网访问家庭云 移动神器RAX3000M路由器变身家庭云…...
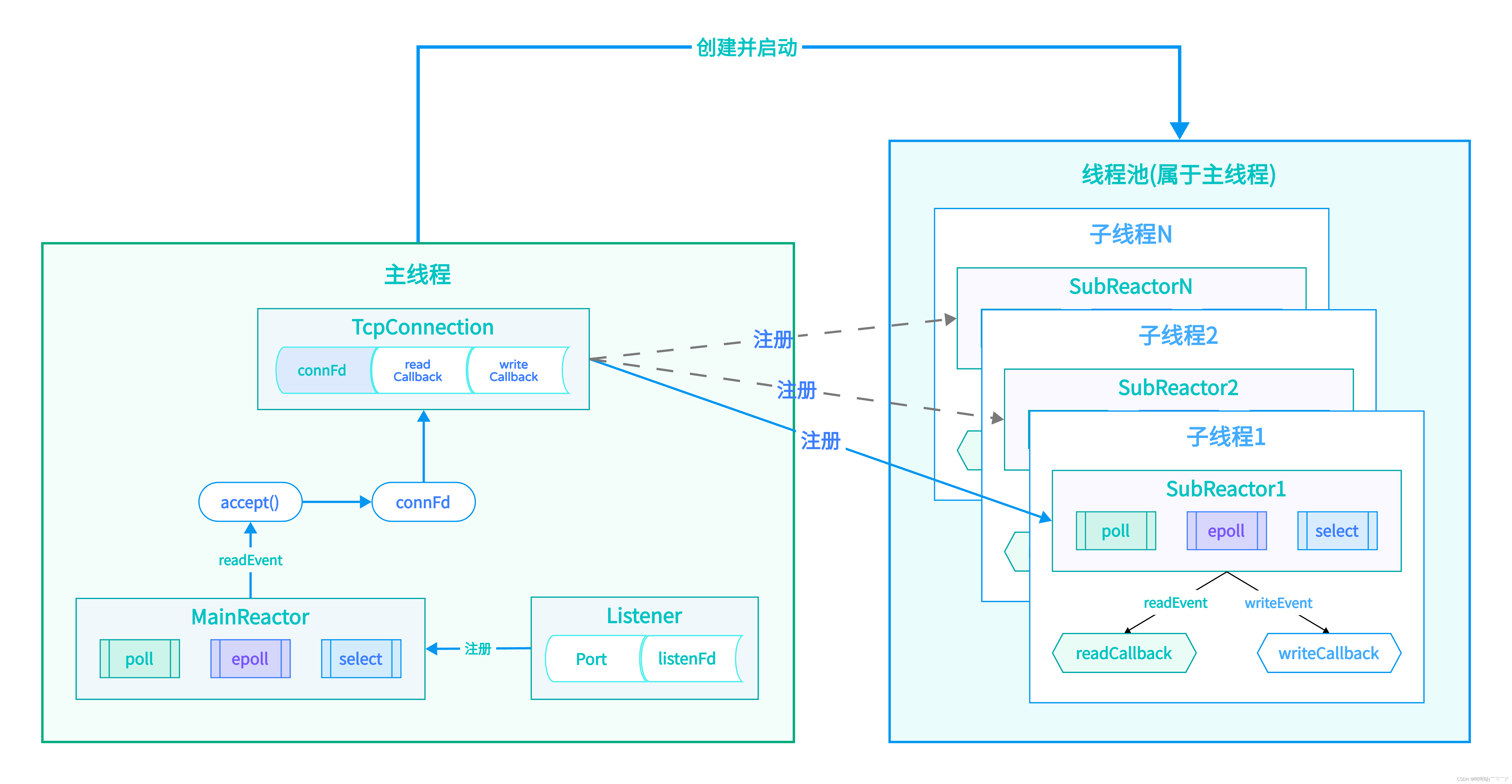
基于多反应堆的高并发服务器【C/C++/Reactor】(中)线程池的启动和从线程池中取出一个反应堆实例
一、线程池的启动 (主线程) // 启动线程池 (主线程) void threadPoolRun(struct ThreadPool* pool) {/*线程池被创建出来之后,接下来就需要让线程池运行起来,其实就是让线程池里的若干个子线程运行起来*//…...

go语言gin框架的基本使用
1.首先在linux环境上安装go环境,这个网上搜搜就行 2.初始化一个go mod,网上搜搜怎么初始化 3.下面go代码的网址和端口绑定自己本机的就行 4.与另一篇CSDN一起食用,效果更好哟---> libcurl的get、post的使用-CSDN博客 package mainimpo…...

TypeScript 从入门到进阶之基础篇(六) 类型(断言 、推论、别名)| 联合类型 | 交叉类型
系列文章目录 TypeScript 从入门到进阶系列 TypeScript 从入门到进阶之基础篇(一) ts基础类型篇TypeScript 从入门到进阶之基础篇(二) ts进阶类型篇TypeScript 从入门到进阶之基础篇(三) 元组类型篇TypeScript 从入门到进阶之基础篇(四) symbol类型篇TypeScript 从入门到进阶…...
:文件管理-文件属性命令)
Linux操作系统基础(14):文件管理-文件属性命令
1. 查看文件属性 stat命令用于显示文件的详细信息,包括文件的权限、所有者、大小、修改时间等。 #1.显示文件信息 stat file.txt#2.显示文件系统状态 stat -f file.txt#3.显示以时间戳的形式文件信息 stat -t file.txt2. 修改文件时间戳 touch命令用于创建新的空…...
metaSPAdes,megahit,IDBA-UB:宏基因组装软件安装与使用
metaSPAdes,megahit,IDBA-UB是目前比较主流的宏基因组组装软件 metaSPAdes安装 GitHub - ablab/spades: SPAdes Genome Assembler #3.15.5的预编译版貌似有问题,使用源码安装试试 wget http://cab.spbu.ru/files/release3.15.5/SPAdes-3.15.5.tar.gz tar -xzf SP…...

Apache、MySQL、PHP编译安装LAMP环境
1. 请简要介绍一下LAMP环境。 LAMP环境是一个在Linux操作系统上搭建的服务器环境组合,由Apache、MySQL、PHP三种软件构成。这种环境是开源的,跨平台的,并且由于各组件经常一起使用,因此具有高度的兼容性。 其中,Apac…...
L1-087:机工士姆斯塔迪奥
题目描述 在 MMORPG《最终幻想14》的副本“乐欲之所瓯博讷修道院”里,BOSS 机工士姆斯塔迪奥将会接受玩家的挑战。 你需要处理这个副本其中的一个机制:NM 大小的地图被拆分为了 NM 个 11 的格子,BOSS 会选择若干行或/及若干列释放技能&#x…...

如何做一个炫酷的Github个人简介(3DContribution)
文章目录 前言3D-Contrib第一步第二步第三步第四步第五步第六步 前言 最近放假了,毕设目前也不太想做,先搞一点小玩意玩玩,让自己的github看起来好看点。也顺便学学这个action是怎么个事。 3D-Contrib 先给大家看一下效果 我的个人主页&am…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...

