HDU 2841:Visible Trees ← 容斥原理
【题目来源】
http://acm.hdu.edu.cn/showproblem.php?pid=2841
【题目描述】
There are many trees forming a m * n grid, the grid starts from (1,1). Farmer Sherlock is standing at (0,0) point. He wonders how many trees he can see.
If two trees and Sherlock are in one line, Farmer Sherlock can only see the tree nearest to him.
【输入格式】
The first line contains one integer t, represents the number of test cases. Then there are multiple test cases. For each test case there is one line containing two integers m and n(1 ≤ m, n ≤ 100000)
【输出格式】
For each test case output one line represents the number of trees Farmer Sherlock can see.
【输入样例】
2
1 1
2 3
【输出样例】
1
5
【算法分析】
在计数时,必须注意无一重复,无一遗漏。为了使重叠部分不被重复计算,人们研究出一种计数方法,这种方法的基本思想是:先不考虑重叠的情况,把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排斥出去,使得计算的结果既无遗漏又无重复,这种计数的方法称为容斥原理。
针对本题,显然,若 (x,y) 能被看到,那么 (k*x, k*y) 都不能被看到(其中,k>1)。
因此,问题转化为求 1<=x<=n 且 1<=y<=m 有多个 <x,y> 满足 gcd(x,y)=1。
那么可以从 1~n 枚举 x,累计 1~m 中与 x 互质的个数。
对 x 分解素因子,容斥一下就可得到结果。
【算法代码】
#include <iostream>
#include <vector>
using namespace std;typedef long long LL;
vector<int> v;
int n,m;void pfac(int x) { //Find all the prime factors of xv.clear();for(int i=2; i*i<=x; i++) {if(x%i==0) {v.push_back(i);while(x%i==0) x/=i;}}if(x>1) v.push_back(x);
}int solve(int x) {int sum=0;for(int i=1; i<(1<<v.size()); i++) {int res=1,cnt=0;for(int j=0; j<v.size(); j++) {if(i & (1<<j)) {res*=v[j];cnt++;}}if(cnt & 1) sum+=x/res;else sum-=x/res;}return sum;
}int main() {int T;cin>>T;while(T--) {scanf("%d %d",&n,&m); //cin>>n>>m;LL ans=m;for(int i=2; i<=n; i++) {pfac(i);ans+=m-solve(m);}printf("%lld\n",ans);}
}/*
in:
2
1 1
2 3out:
1
5
*/
【参考文献】
https://www.cnblogs.com/00isok/p/10358598.html
https://blog.csdn.net/weixin_53746961/article/details/121175561
https://blog.csdn.net/weixin_43846139/article/details/105517437
https://www.cnblogs.com/crackpotisback/p/4846909.html
http://www.manongjc.com/detail/39-wpncookuuhcoyui.html
https://blog.csdn.net/weixin_30710457/article/details/98919034
相关文章:

HDU 2841:Visible Trees ← 容斥原理
【题目来源】http://acm.hdu.edu.cn/showproblem.php?pid2841【题目描述】 There are many trees forming a m * n grid, the grid starts from (1,1). Farmer Sherlock is standing at (0,0) point. He wonders how many trees he can see. If two trees and Sherlock are in…...
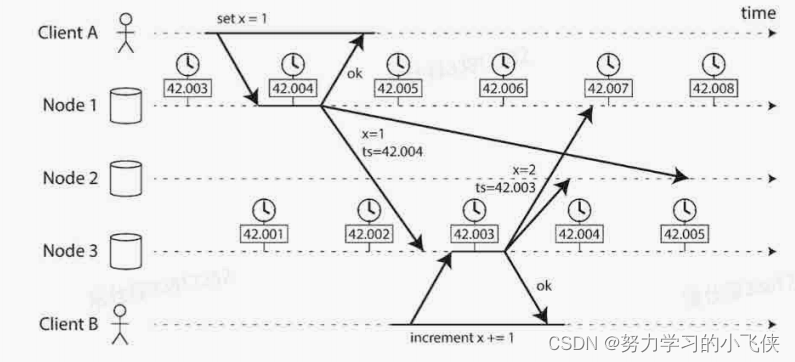
分布式数据之复制(Replication)
1.简介 1.1简介——使用复制的目的 在分布式系统中,数据通常需要被分散在多台机器上,主要为了达到以下目的: 扩展性,数据量因读写负载巨大,一台机器无法承载,数据分散在多台机器 上可以有效地进行负载均衡…...

【多线程】
文章目录 一、线程与进程的概念:二、多线程实现三、线程锁四、线程数量的设置 一、线程与进程的概念: 简单理解 假设总共有3个孩子需要喂饭,孩子每吃一口饭需要咀嚼消化一下。 多线程方案: 雇佣1个保姆,在喂A孩子吃饭…...
基于Vue开发的一个仿京东电商购物平台系统(附源码下载)
电商购物平台项目 项目完整源码下载 基于Vue开发的一个仿京东电商购物平台系统 Build Setup # csdn下载该项目源码压缩包 解压重命名为sangpinghui_project# 进入项目目录 cd sangpinghui_project# 安装依赖 npm install# 建议不要直接使用 cnpm 安装以来,会有各…...

Nginx多ip部署多站点
目录 1.修改网卡配置信息 2.修改主要配置文件nginx.conf 1.修改网卡配置信息 1)来到网卡配置文件存放目录下 cd /etc/sysconfig/network-scripts/ 2)对 ifcfg-ens33 文件进行配置修改前先进行备份 cp ifcfg-ens33 ifcfg-ens33.default 3)先修改成最小配置,使用 d…...
Unity SVN更新提交小工具
Unity SVN更新提交小工具 前言使用说明必要前提源码参数说明 感谢 前言 Unity开发时每次都要到文件夹中操作SVN,做了一个小工具能够在Editor中直接操作。 使用说明 必要前提 前提是要安装好SVN,在文件夹右键能够看到安装的SVN 源码 using System…...

听GPT 讲Rust源代码--compiler(19)
File: rust/compiler/rustc_target/src/spec/mips_unknown_linux_gnu.rs 该文件(rust/compiler/rustc_target/src/spec/mips_unknown_linux_gnu.rs)是Rust编译器针对MIPS架构上的Linux系统的目标描述文件。它的作用是定义了在这个目标上编译时的一些配置…...

redis单机部署
一、下载redis压缩包tar.gz 官网下载,现在一般用6.x以上版本 二、上传指定目录,解压缩 #假如上传到redis用户的家目录 cd /home/redis tar -zxvf redis-6.2.14.tar.gz 三、进入解压缩目录,进行编译 cd redis-6.2.14 make &&a…...

el-upload上传文件
需求:选中或拖拽文件后,使用http-request属性实现自动上传,并根据后端传回来的结果显示错误和控制fileList的显示,如果后端返回成功,则文件显示在文件列表处,如果后端返回失败,则文件列表不显示…...
算法导论复习——CHP16 贪心算法
定义 每一步都做出当前看来最优的操作。 问题引入——活动选择问题 问题描述 活动选择问题就是对给定的包含n个活动的集合S,在已知每个活动开始时间和结束时间的条件下,从中选出最多可兼容活动的子集合,称为最大兼容活动集合。 不失一般性&a…...
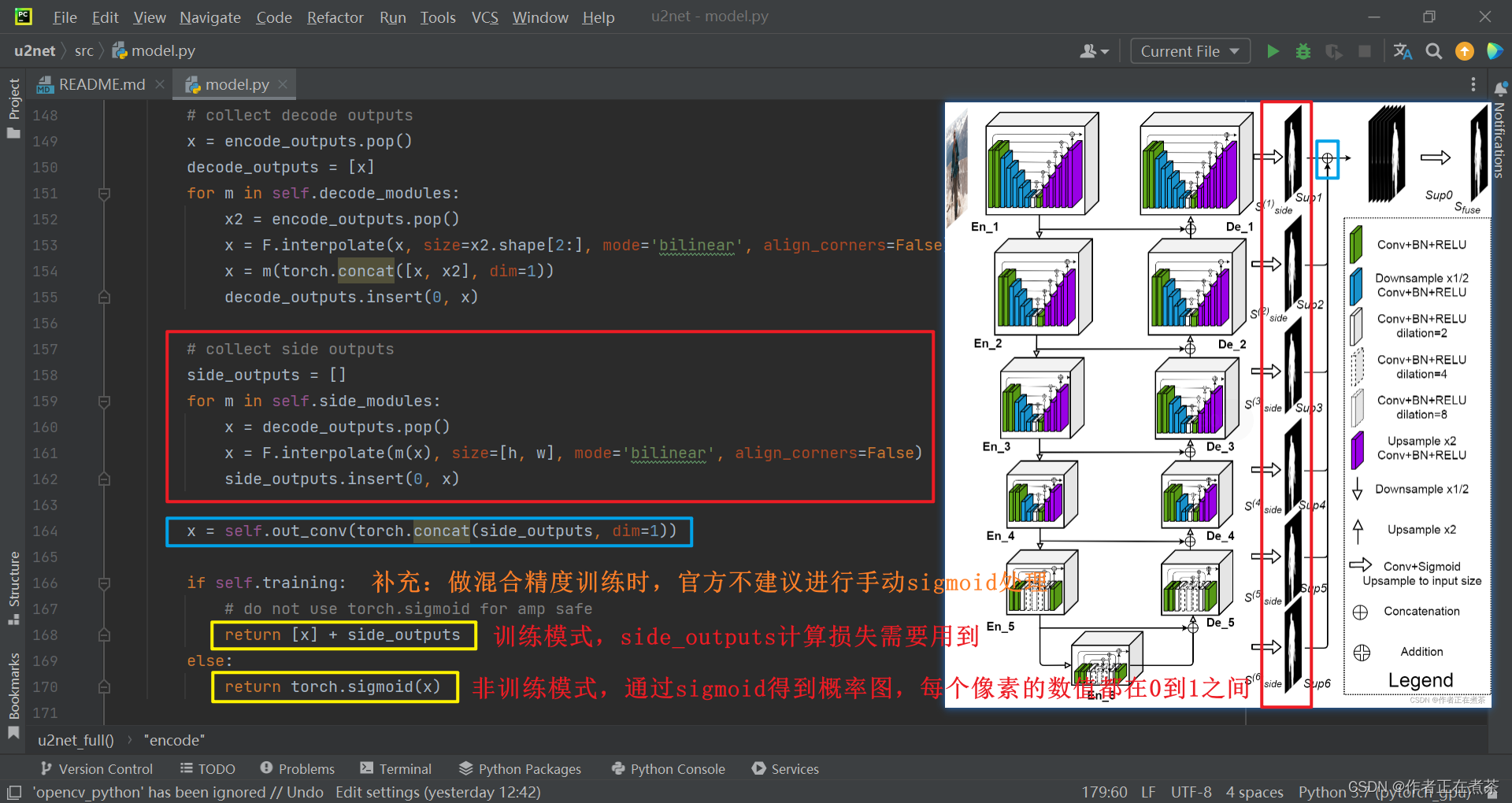
【霹雳吧啦】手把手带你入门语义分割の番外12:U2-Net 源码讲解(PyTorch)—— 网络的搭建
目录 前言 Preparation 一、U2-Net 网络结构图 二、U2-Net 网络源代码 1、model.py (1)ConvBNReLU 类 (2)DownConvBNReLU 类 (3)UpConvBNReLU 类 (4)RSU 类 & RSU4F 类…...

phpstudy面板Table ‘mysql.proc‘ doesn‘t exist解决办法
原因分析:误删了mysql数据库 解决办法如下: 1、停止服务 2、先把mysql文件夹下的data文件夹备份,因为data文件里存有数据库文件。然后再删除data文件。 3、cmd管理员命令进入到mysql中的bin目录下 ,执行mysqld --initialize-…...

网安入门09-Sql注入(绕过方法梳理)
ByPass SQL注入ByPass是指攻击者通过各种手段绕过应用程序中已经实施的SQL注入防御措施,例如输入恶意数据、修改请求头等方式,绕过过滤、转义、限制等操作,从而成功地执行恶意SQL语句。攻击者使用SQL注入ByPass技术可以让应用程序的防御措施…...
本地计算机 上的 My5OL808 服务启动后停止,某些服务在未由其他服务或程序使用时将自动停止
客户反馈说mysql启动不了,报错信息: 本地计算机 上的 My5OL808 服务启动后停止,某些服务在未由其他服务或程序使用时将自动停止。 查了不少资料,最后分析问题是这样的,手动或者重复安装mysql时,创建了多个…...
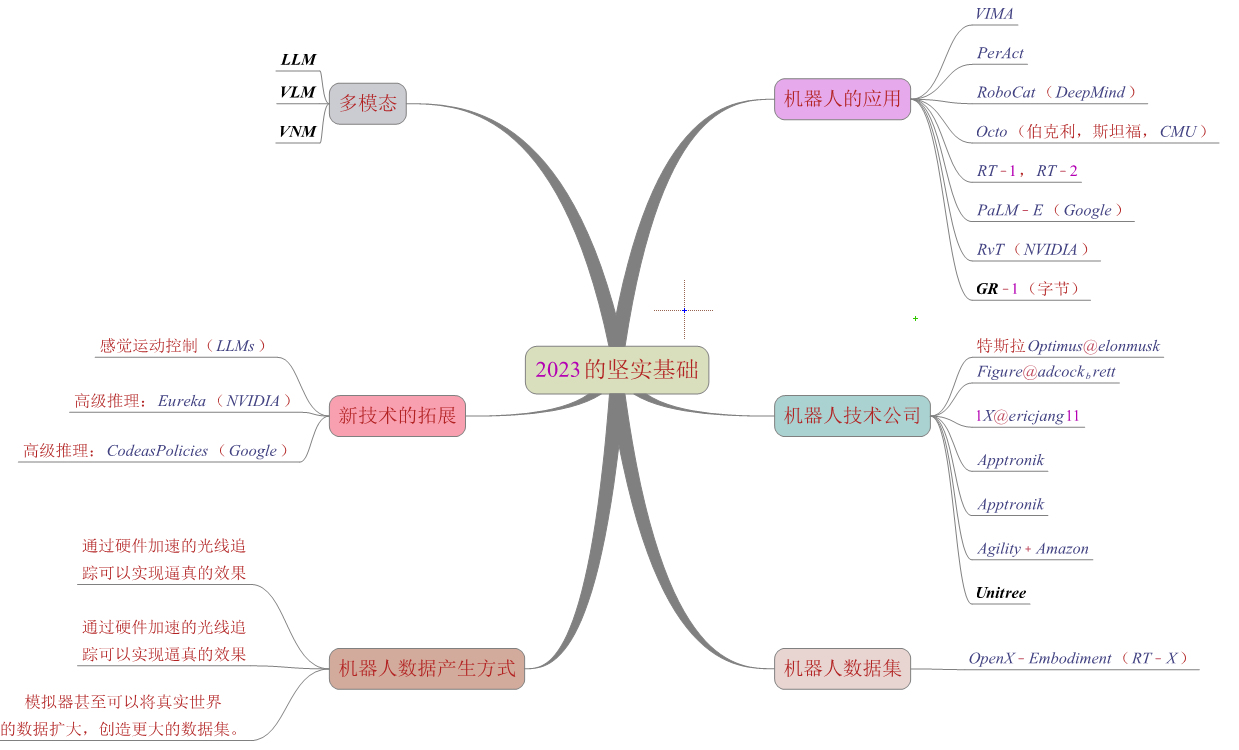
2023机器人行业总结,2024机器人崛起元年(具身智能)
2023总结: 1.Chatgpt引爆了通用人工智能,最大的受益者或是机器人,2023年最热门的创业赛道便是人形机器人,优必选更是成为人形机器人上市第一股, 可以说2023年是机器人开启智能化的元年,而2024则将成为机器…...

go 语言中的类型判断
_. ok : interface{}(a).(B)此语句用于判断对象a是否是B类型 也可以判断对象a是否实现了B接口 package mainimport "fmt"type Pet interface {SetName(name string)Name() stringCategory() string } type Dog struct {name string }func (dog *Dog) SetName(name …...
java基于ssm的房源管理系统+vue论文
目 录 目 录 I 摘 要 III ABSTRACT IV 1 绪论 1 1.1 课题背景 1 1.2 研究现状 1 1.3 研究内容 2 2 系统开发环境 3 2.1 vue技术 3 2.2 JAVA技术 3 2.3 MYSQL数据库 3 2.4 B/S结构 4 2.5 SSM框架技术 4 3 系统分析 5 3.1 可行性分析 5 3.1.1 技术可行性 5 3.1.2 操作可行性 5 3…...
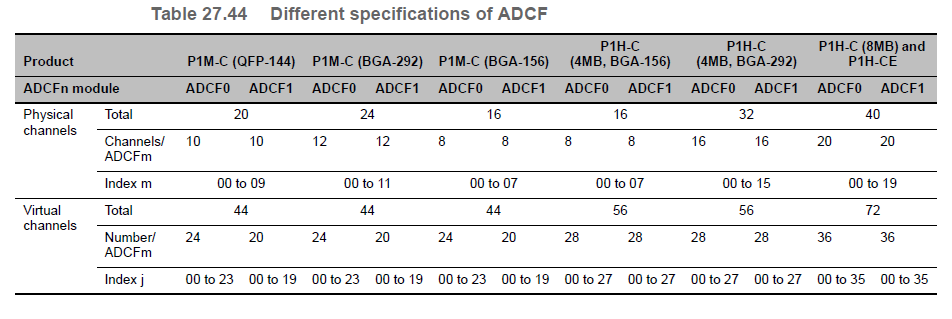
RH850P1X芯片学习笔记-A/D Converter (ADCF)
文章目录 Features of RH850/P1x-C ADCFNumber of UnitsRegister Base AddressClock SupplyInterrupts and DMAHardware ResetExternal Input/Output SignalsVirtual Channel OverviewFunctional OverviewBlock DiagramPhysical Channels, Virtual Channels and Scan Groups Re…...

38 调优kafka
操作系统调优 1.禁止atime更新,减少文件系统的写操作。 mount -o noatime 2.选择高性能的文件系统,如ext4或者XFS 3.swap空间设置,将swappniness设置成很小的一个值比如1~10,防止linux OOM Killer 开启随意杀掉进程。…...

java推荐系统:好友推荐思路
1.表的设计 表里面就两个字段,一个字段是用户id,另外一个字段是好友id,假如A跟B互为好友,那在数据库里面就会有两条数据 2.推荐好友思路 上面的图的意思是:h跟a的互为好友,a跟b,c&am…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...
