秋招复习之堆
目录
前言
堆
堆的常用操作
堆的实现(大根堆)
1. 堆的存储与表示
2. 访问堆顶元素
3. 元素入堆
4. 堆顶元素出堆
Top-k 问题
方法一:遍历选择
方法二:排序
方法三:堆
总结
前言
秋招复习之堆。
堆
「堆 heap」是一种满足特定条件的完全二叉树,主要可分为两种类型,如图所示。
- 「小顶堆 min heap」:任意节点的值 ≤ 其子节点的值。
- 「大顶堆 max heap」:任意节点的值 ≥ 其子节点的值。

堆作为完全二叉树的一个特例,具有以下特性。
- 最底层节点靠左填充,其他层的节点都被填满。
- 我们将二叉树的根节点称为“堆顶”,将底层最靠右的节点称为“堆底”。
- 对于大顶堆(小顶堆),堆顶元素(根节点)的值是最大(最小)的。
堆的常用操作
许多编程语言提供的是「优先队列 priority queue」,这是一种抽象的数据结构,定义为具有优先级排序的队列。
实际上,堆通常用于实现优先队列,大顶堆相当于元素按从大到小的顺序出队的优先队列。从使用角度来看,我们可以将“优先队列”和“堆”看作等价的数据结构。

在实际应用中,我们可以直接使用编程语言提供的堆类(或优先队列类)。
类似于排序算法中的“从小到大排列”和“从大到小排列”,我们可以通过设置一个 flag 或修改 Comparator 实现“小顶堆”与“大顶堆”之间的转换。代码如下所示:
/* 初始化堆 */
// 初始化小顶堆
Queue<Integer> minHeap = new PriorityQueue<>();
// 初始化大顶堆(使用 lambda 表达式修改 Comparator 即可)
Queue<Integer> maxHeap = new PriorityQueue<>((a, b) -> b - a);/* 元素入堆 */
maxHeap.offer(1);
maxHeap.offer(3);
maxHeap.offer(2);
maxHeap.offer(5);
maxHeap.offer(4);/* 获取堆顶元素 */
int peek = maxHeap.peek(); // 5/* 堆顶元素出堆 */
// 出堆元素会形成一个从大到小的序列
peek = maxHeap.poll(); // 5
peek = maxHeap.poll(); // 4
peek = maxHeap.poll(); // 3
peek = maxHeap.poll(); // 2
peek = maxHeap.poll(); // 1/* 获取堆大小 */
int size = maxHeap.size();/* 判断堆是否为空 */
boolean isEmpty = maxHeap.isEmpty();/* 输入列表并建堆 */
minHeap = new PriorityQueue<>(Arrays.asList(1, 3, 2, 5, 4));/* 初始化堆 */
// 初始化小顶堆
priority_queue<int, vector<int>, greater<int>> minHeap;
// 初始化大顶堆
priority_queue<int, vector<int>, less<int>> maxHeap;/* 元素入堆 */
maxHeap.push(1);
maxHeap.push(3);
maxHeap.push(2);
maxHeap.push(5);
maxHeap.push(4);/* 获取堆顶元素 */
int peek = maxHeap.top(); // 5/* 堆顶元素出堆 */
// 出堆元素会形成一个从大到小的序列
maxHeap.pop(); // 5
maxHeap.pop(); // 4
maxHeap.pop(); // 3
maxHeap.pop(); // 2
maxHeap.pop(); // 1/* 获取堆大小 */
int size = maxHeap.size();/* 判断堆是否为空 */
bool isEmpty = maxHeap.empty();/* 输入列表并建堆 */
vector<int> input{1, 3, 2, 5, 4};
priority_queue<int, vector<int>, greater<int>> minHeap(input.begin(), input.end());堆的实现(大根堆)
1. 堆的存储与表示
完全二叉树非常适合用数组来表示。由于堆正是一种完全二叉树,因此我们将采用数组来存储堆。

将索引映射公式封装成函数
/* 获取左子节点的索引 */
int left(int i) {return 2 * i + 1;
}/* 获取右子节点的索引 */
int right(int i) {return 2 * i + 2;
}/* 获取父节点的索引 */
int parent(int i) {return (i - 1) / 2; // 向下整除
}/* 获取左子节点的索引 */
int left(int i) {return 2 * i + 1;
}/* 获取右子节点的索引 */
int right(int i) {return 2 * i + 2;
}/* 获取父节点的索引 */
int parent(int i) {return (i - 1) / 2; // 向下整除
}2. 访问堆顶元素
/* 访问堆顶元素 */
int peek() {return maxHeap.get(0);
}/* 访问堆顶元素 */
int peek() {return maxHeap[0];
}3. 元素入堆
给定元素 val ,我们首先将其添加到堆底。添加之后,由于 val 可能大于堆中其他元素,堆的成立条件可能已被破坏,因此需要修复从插入节点到根节点的路径上的各个节点,这个操作被称为「堆化 heapify」。
考虑从入堆节点开始,从底至顶执行堆化。如图所示,我们比较插入节点与其父节点的值,如果插入节点更大,则将它们交换。然后继续执行此操作,从底至顶修复堆中的各个节点,直至越过根节点或遇到无须交换的节点时结束。(就是一直和父比较,大就换)

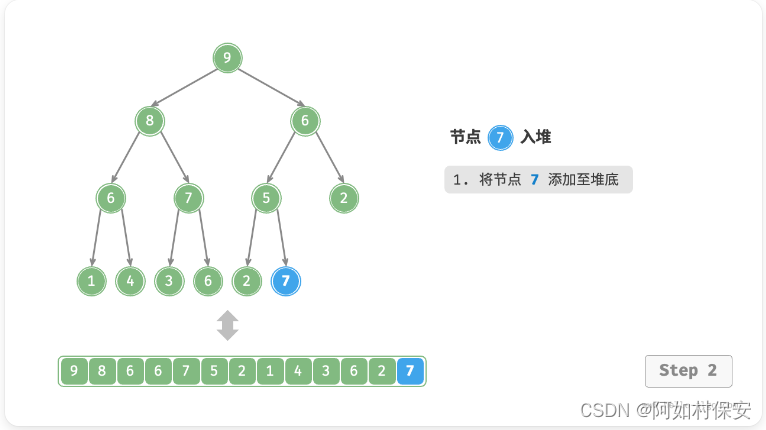
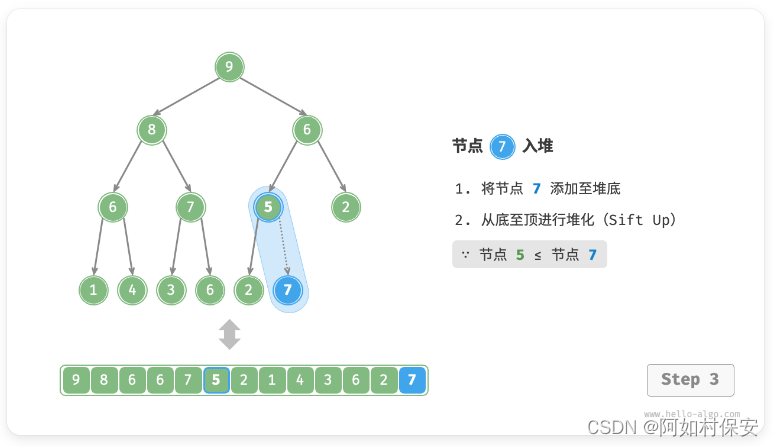

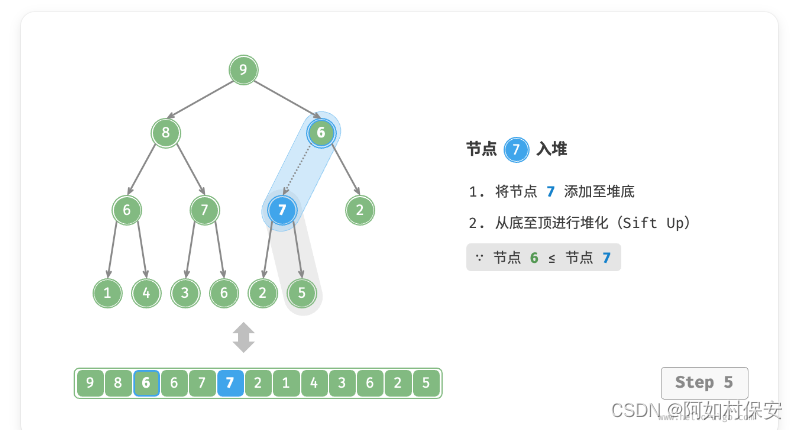

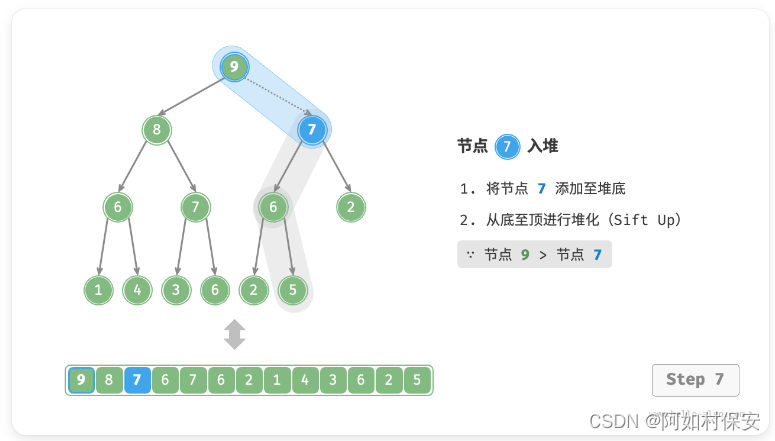


设节点总数为 n ,则树的高度为 O(logN) 。由此可知,堆化操作的循环轮数最多为 O(logN) ,元素入堆操作的时间复杂度为 O(logN) 。
/* 元素入堆 */
void push(int val) {// 添加节点maxHeap.add(val);// 从底至顶堆化siftUp(size() - 1);
}/* 从节点 i 开始,从底至顶堆化 */
void siftUp(int i) {while (true) {// 获取节点 i 的父节点int p = parent(i);// 当“越过根节点”或“节点无须修复”时,结束堆化if (p < 0 || maxHeap.get(i) <= maxHeap.get(p))break;// 交换两节点swap(i, p);// 循环向上堆化i = p;}
}/* 元素入堆 */
void push(int val) {// 添加节点maxHeap.push_back(val);// 从底至顶堆化siftUp(size() - 1);
}/* 从节点 i 开始,从底至顶堆化 */
void siftUp(int i) {while (true) {// 获取节点 i 的父节点int p = parent(i);// 当“越过根节点”或“节点无须修复”时,结束堆化if (p < 0 || maxHeap[i] <= maxHeap[p])break;// 交换两节点swap(maxHeap[i], maxHeap[p]);// 循环向上堆化i = p;}
}4. 堆顶元素出堆
堆顶元素是二叉树的根节点,即列表首元素。如果我们直接从列表中删除首元素,那么二叉树中所有节点的索引都会发生变化,这将使得后续使用堆化进行修复变得困难。为了尽量减少元素索引的变动,我们采用以下操作步骤。
- 交换堆顶元素与堆底元素(交换根节点与最右叶节点)。
- 交换完成后,将堆底从列表中删除(注意,由于已经交换,因此实际上删除的是原来的堆顶元素)。
- 从根节点开始,从顶至底执行堆化。
如图所示,“从顶至底堆化”的操作方向与“从底至顶堆化”相反,我们将根节点的值与其两个子节点的值进行比较,将最大的子节点与根节点交换。然后循环执行此操作,直到越过叶节点或遇到无须交换的节点时结束。





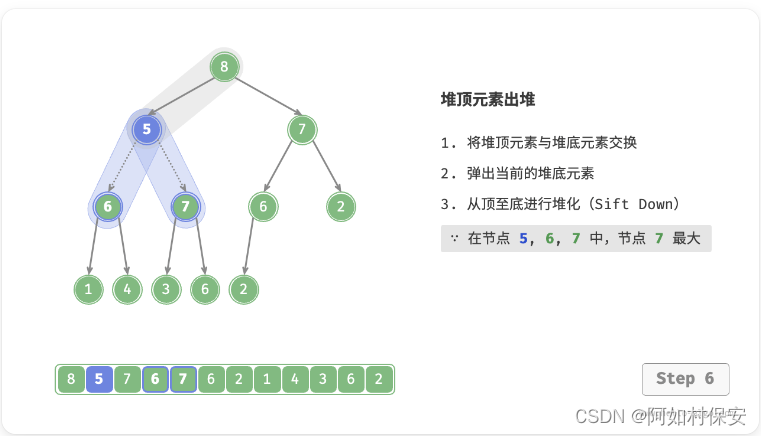
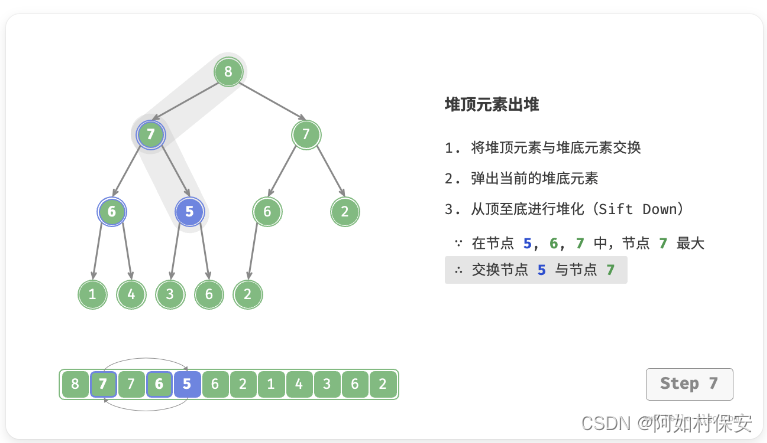



与元素入堆操作相似,堆顶元素出堆操作的时间复杂度也为 O(logn) 。代码如下所示:
/* 元素出堆 */
int pop() {// 判空处理if (isEmpty())throw new IndexOutOfBoundsException();// 交换根节点与最右叶节点(交换首元素与尾元素)swap(0, size() - 1);// 删除节点int val = maxHeap.remove(size() - 1);// 从顶至底堆化siftDown(0);// 返回堆顶元素return val;
}/* 从节点 i 开始,从顶至底堆化 */
void siftDown(int i) {while (true) {// 判断节点 i, l, r 中值最大的节点,记为 maint l = left(i), r = right(i), ma = i;if (l < size() && maxHeap.get(l) > maxHeap.get(ma))ma = l;if (r < size() && maxHeap.get(r) > maxHeap.get(ma))ma = r;// 若节点 i 最大或索引 l, r 越界,则无须继续堆化,跳出if (ma == i)break;// 交换两节点swap(i, ma);// 循环向下堆化i = ma;}
}/* 元素出堆 */
void pop() {// 判空处理if (isEmpty()) {throw out_of_range("堆为空");}// 交换根节点与最右叶节点(交换首元素与尾元素)swap(maxHeap[0], maxHeap[size() - 1]);// 删除节点maxHeap.pop_back();// 从顶至底堆化siftDown(0);
}/* 从节点 i 开始,从顶至底堆化 */
void siftDown(int i) {while (true) {// 判断节点 i, l, r 中值最大的节点,记为 maint l = left(i), r = right(i), ma = i;if (l < size() && maxHeap[l] > maxHeap[ma])ma = l;if (r < size() && maxHeap[r] > maxHeap[ma])ma = r;// 若节点 i 最大或索引 l, r 越界,则无须继续堆化,跳出if (ma == i)break;swap(maxHeap[i], maxHeap[ma]);// 循环向下堆化i = ma;}
}Top-k 问题
Q:给定一个长度为 n的无序数组 nums ,请返回数组中最大的 k个元素。
方法一:遍历选择
其时间复杂度趋向于O(n2) ,非常耗时。

当 k=n 时,可以得到完整的有序序列,此时等价于“选择排序”算法。
方法二:排序
如图所示,我们可以先对数组 nums 进行排序,再返回最右边的 k 个元素,时间复杂度为 O(nlogn) 。
显然,该方法“超额”完成任务了,因为我们只需找出最大的k个元素即可,而不需要排序其他元素。

方法三:堆
可以基于堆更加高效地解决 Top-k 问题,流程如图所示。
- 初始化一个小顶堆,其堆顶元素最小。
- 先将数组的前 k 个元素依次入堆。
- 从第 k+1 个元素开始,若当前元素大于堆顶元素,则将堆顶元素出堆,并将当前元素入堆。
- 遍历完成后,堆中保存的就是最大k 个元素。
天才!!!


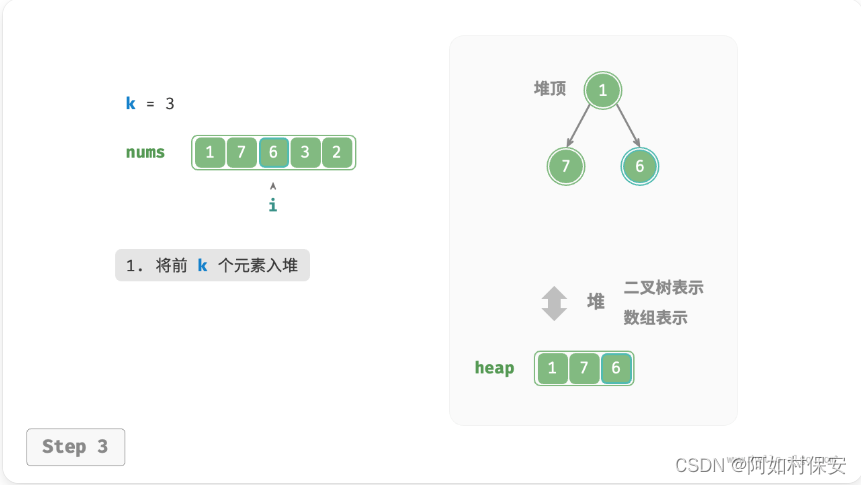



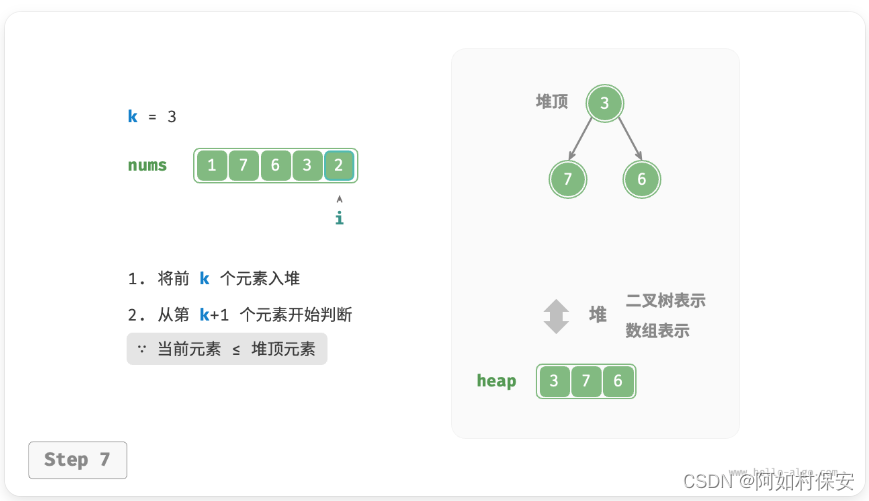


/* 基于堆查找数组中最大的 k 个元素 */
Queue<Integer> topKHeap(int[] nums, int k) {// 初始化小顶堆Queue<Integer> heap = new PriorityQueue<Integer>();// 将数组的前 k 个元素入堆for (int i = 0; i < k; i++) {heap.offer(nums[i]);}// 从第 k+1 个元素开始,保持堆的长度为 kfor (int i = k; i < nums.length; i++) {// 若当前元素大于堆顶元素,则将堆顶元素出堆、当前元素入堆if (nums[i] > heap.peek()) {heap.poll();heap.offer(nums[i]);}}return heap;
}/* 基于堆查找数组中最大的 k 个元素 */
priority_queue<int, vector<int>, greater<int>> topKHeap(vector<int> &nums, int k) {// 初始化小顶堆priority_queue<int, vector<int>, greater<int>> heap;// 将数组的前 k 个元素入堆for (int i = 0; i < k; i++) {heap.push(nums[i]);}// 从第 k+1 个元素开始,保持堆的长度为 kfor (int i = k; i < nums.size(); i++) {// 若当前元素大于堆顶元素,则将堆顶元素出堆、当前元素入堆if (nums[i] > heap.top()) {heap.pop();heap.push(nums[i]);}}return heap;
}总共执行了 n轮入堆和出堆,堆的最大长度为 k ,因此时间复杂度为 O(nlogk) 。该方法的效率很高,当 k 较小时,时间复杂度趋向 O(n) ;当 n 较大时,时间复杂度不会超过 O(nlogn) 。
另外,该方法适用于动态数据流的使用场景。在不断加入数据时,我们可以持续维护堆内的元素,从而实现最大的 k个元素的动态更新。
总结
- 堆是一棵完全二叉树,根据成立条件可分为大顶堆和小顶堆。大(小)顶堆的堆顶元素是最大(小)的。
- 优先队列的定义是具有出队优先级的队列,通常使用堆来实现。
- 堆的常用操作及其对应的时间复杂度包括:元素入堆 O(logn)、堆顶元素出堆 O(logn) 和访问堆顶元素 O(1) 等。
- 完全二叉树非常适合用数组表示,因此我们通常使用数组来存储堆。
- 堆化操作用于维护堆的性质,在入堆和出堆操作中都会用到。
- 输入 n 个元素并建堆的时间复杂度可以优化至 O(n) ,非常高效。
- Top-k 是一个经典算法问题,可以使用堆数据结构高效解决,时间复杂度为 O(nlogK) 。

相关文章:

秋招复习之堆
目录 前言 堆 堆的常用操作 堆的实现(大根堆) 1. 堆的存储与表示 2. 访问堆顶元素 3. 元素入堆 4. 堆顶元素出堆 Top-k 问题 方法一:遍历选择 方法二:排序 方法三:堆 总结 前言 秋招复习之堆。 堆 「堆 heap…...
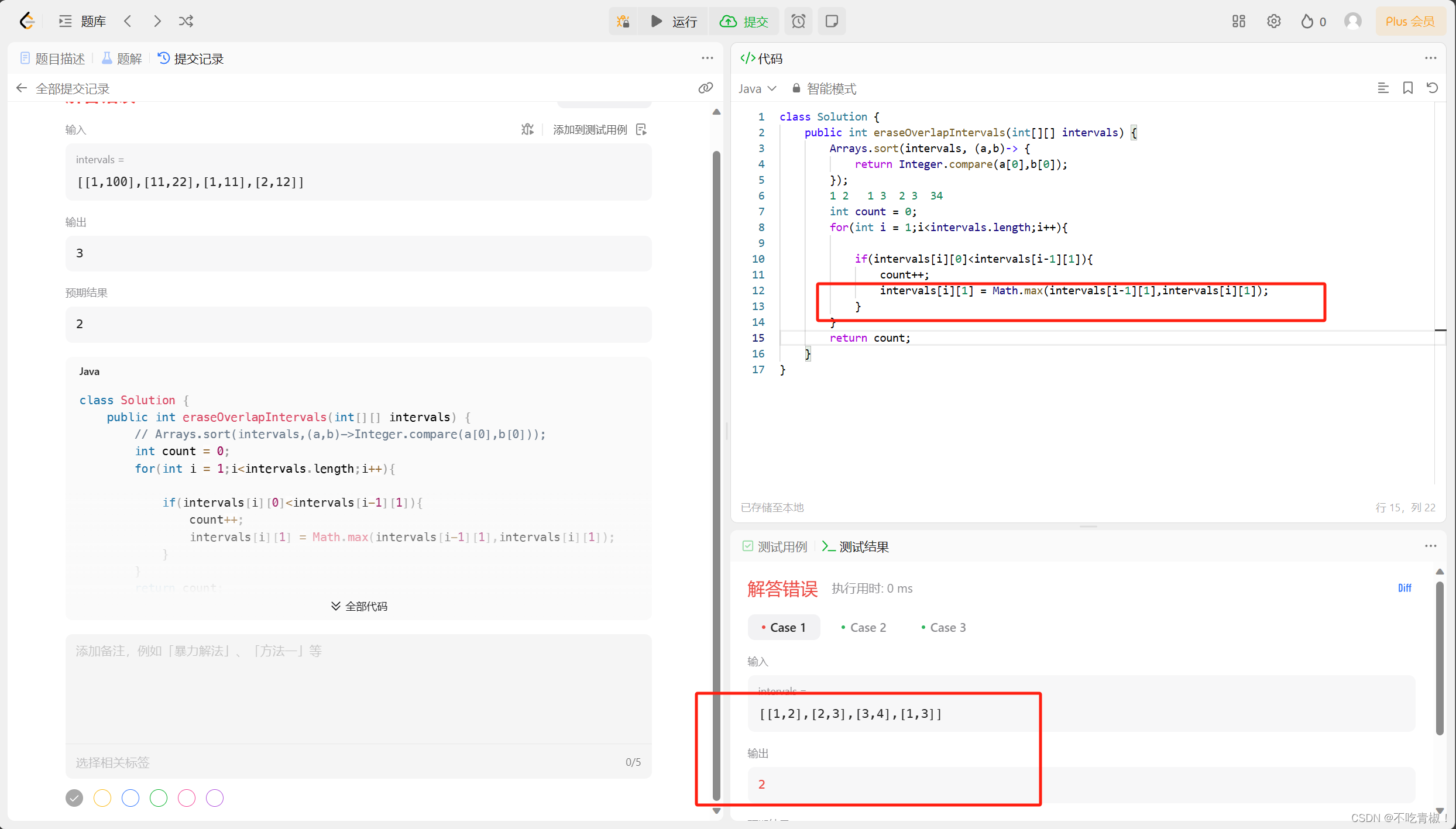
算法训练营Day36(贪心-重叠区间)
都算是 重叠区间 问题,大家可以好好感受一下。 都属于那种看起来好复杂,但一看贪心解法,惊呼:这么巧妙! 还是属于那种,做过了也就会了,没做过就很难想出来。 不过大家把如下三题做了之后&#…...

如何利用Oracle官方网站不登录账号下载和安装非最新版本的JDK(版本自由选择)
一、JDK概述 JDK(Java Development Kit)是Java开发工具集,是针对Java编程语言的软件开发环境。它包含了Java编译器、JRE(Java运行时环境)以及其他一些用于开发、调试和测试Java应用程序的工具,是Java开发人…...
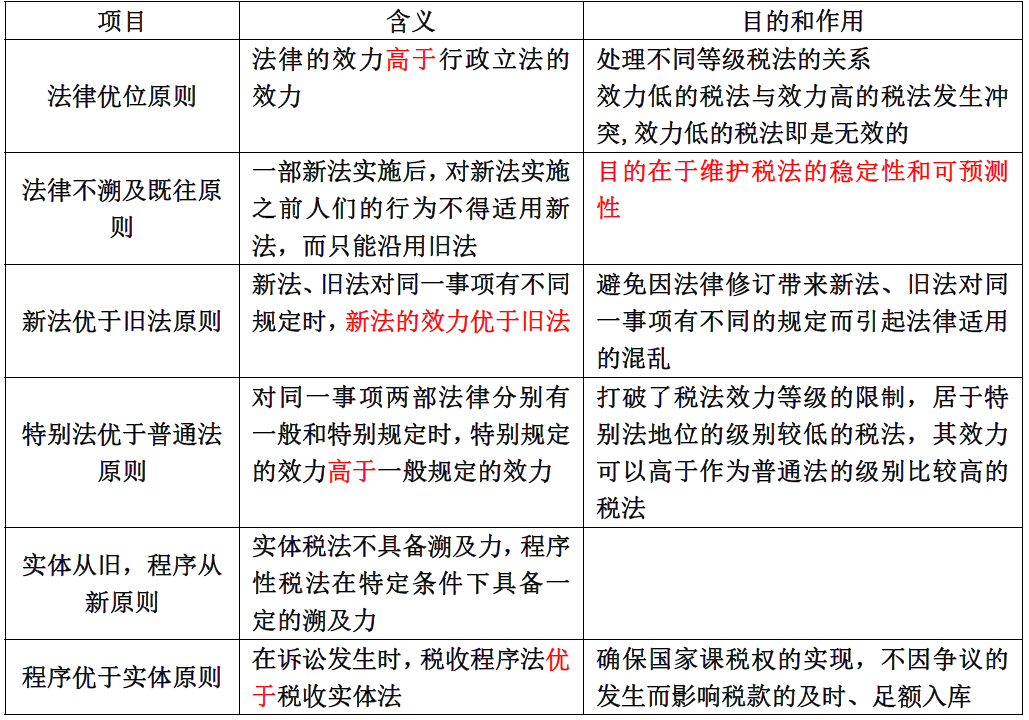
税法相关的基础知识
文章目录 税法原则1.税法基本原则2.税法适用原则 来和大家聊聊税法相关的基础知识 税法原则 1.税法基本原则 2.税法适用原则...

ListNode 2487. 从链表中移除节点,单调栈的应用
一、题目 1、题目描述 给你一个链表的头节点 head 。 移除每个右侧有一个更大数值的节点。 返回修改后链表的头节点 head 。 2、接口描述 /*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nu…...
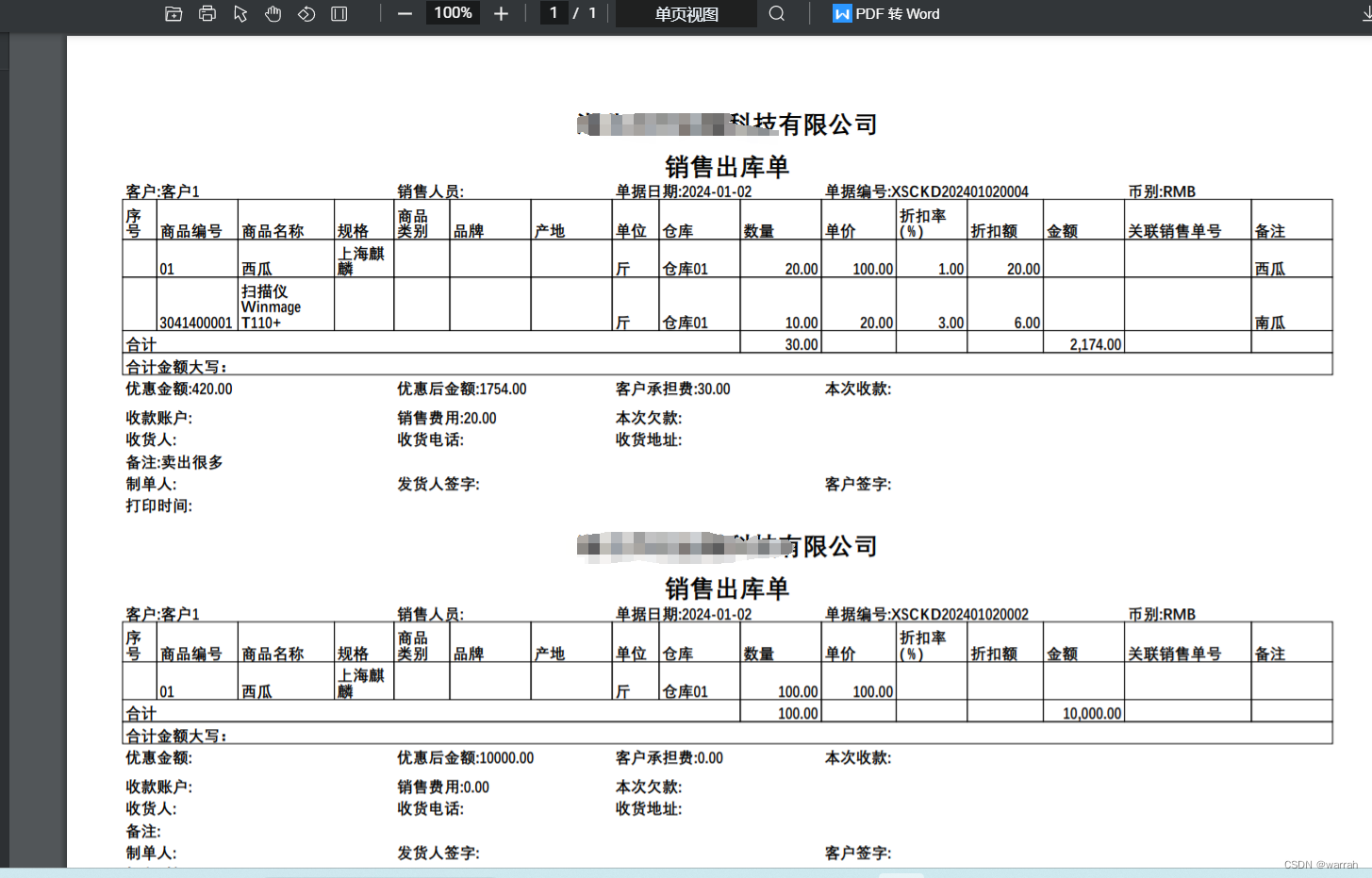
vue3中pdf打印问题处理
1 get请求参数问题 之前的请求是post得不到参数,今天发现的问题很奇怪,从前端进入网关,网关居然得不到参数。 前端代码 const print () > {let linkUrlStr proxy.$tool.getUrlStr(proxy.$api.invOrder.psiInvOrder.printSalOutstock,{a…...
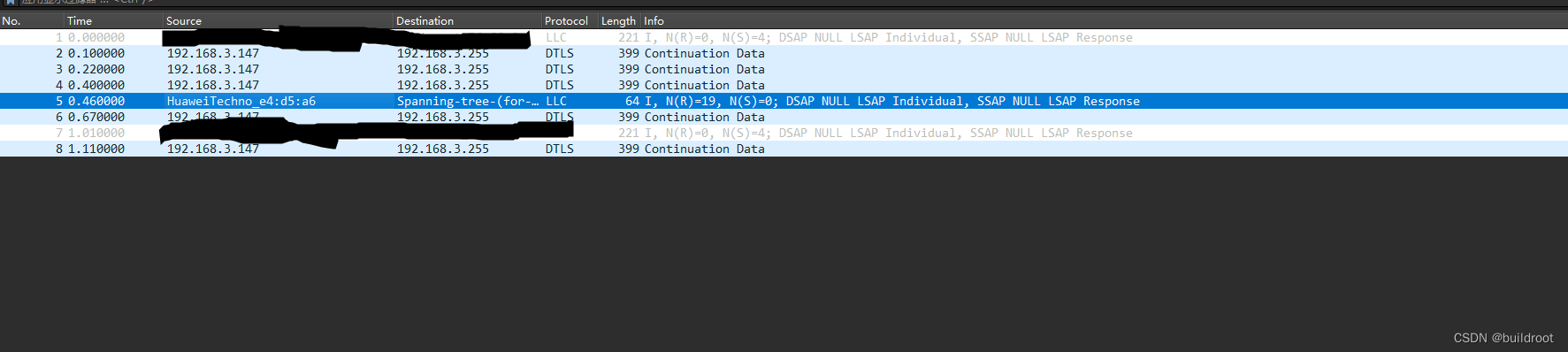
如何向嵌入式设备中添加tcpdump工具
说明:tcpdump是一个在网络设备调试中一个非常重要的工具,它并不像hexdump等工具集成在busybox里面,也不像其他的软件一样只需要依赖linux标准的库就可以实现,它需要pcap相关的库和加密的相关库。 本文主要是基于realtek 83系列的…...

伦茨科技Apple Find My认证芯片-ST17H6x芯片
深圳市伦茨科技有限公司(以下简称“伦茨科技”)发布ST17H6x Soc平台。成为继Nordic之后全球第二家取得Apple Find My「查找」认证的芯片厂家,该平台提供可通过Apple Find My认证的Apple查找(Find My)功能集成解决方案。…...
uni-app 前后端调用实例 基于Springboot 数据列表显示实现
锋哥原创的uni-app视频教程: 2023版uniapp从入门到上天视频教程(Java后端无废话版),火爆更新中..._哔哩哔哩_bilibili2023版uniapp从入门到上天视频教程(Java后端无废话版),火爆更新中...共计23条视频,包括:第1讲 uni…...

python渗透工具编写学习笔记:10、网络爬虫基础/多功能编写
目录 前言 10.1 概念 10.2 调度器/解析器 10.3 存储器/去重器 10.4 日志模块 10.5 反爬模块 10.6 代理模块 前言 在渗透工具中,网络爬虫有着不可忽视的作用,它能够快速而精准的搜寻、提取我们所需要的信息并按照我们所需要的格式排列,…...
Python武器库开发-武器库篇之子域名扫描器开发(四十一)
Python武器库开发-武器库篇之子域名扫描器开发(四十一) 在我们做红队攻防或者渗透测试的过程中,信息收集往往都是第一步的,有人说:渗透的本质就是信息收集,前期好的信息收集很大程度上决定了渗透的质量和攻击面,本文将…...

通俗易懂的15个Java Lambda表达式案例
文章目录 1. **实现Runnable接口**:2. **事件监听器**(如Swing中的ActionListener):3. **集合遍历**(使用forEach方法):4. **过滤集合**(使用Stream API):5. …...
)
十七:爬虫-JS逆向(上)
1、什么是JS、JS反爬是什么?JS逆向是什么? JS:JS全称JavaScript是互联网上最流行的脚本语言,这门语言可用于HTML 和 web,更可广泛用于服务器、PC、笔记本电脑、平板电脑和智能手机等设备。JavaScript 是一种轻量级的编程语言。JavaScript 是…...

How to implement anti-crawler strategies to protect site data
How to implement anti-crawler strategies to protect site data 信息校验型反爬虫User-Agent反爬虫Cookie反爬虫签名验证反爬虫WebSocket握手验证反爬虫WebSocket消息校验反爬虫WebSocket Ping反爬虫 动态渲染反爬虫文本混淆反爬虫图片伪装反爬虫CSS偏移反爬虫SVG映射反爬虫字…...

王国维的人生三境界,这一生至少当一次傻瓜
一、人生三境界 古今之成大事业、大学问者,必经过三种之境界。“昨夜西风凋碧树,独上高楼,望尽天涯路。”此第一境也。“衣带渐宽终不悔,为伊消得人憔悴。”此第二境也。“众里寻他千百度,蓦然回首,那人却…...
Jmeter二次开发实操问题汇总(JDK问题,jar包问题)
前提 之前写过一篇文章:https://qa-lsq.blog.csdn.net/article/details/119782694 只是简单尝试了一下生成一个随机手机号码。 但是如果在工作中一个实际场景要用的二次开发,可能会遇到一些问题。 比如这样一个场景: Mobile或者前端调用部分…...

网络安全B模块(笔记详解)- 数字取证
数据分析数字取证-attack 1.使用Wireshark查看并分析Windows 7桌面下的attack.pcapng数据包文件,通过分析数据包attack.pcapng找出恶意用户的IP地址,并将恶意用户的IP地址作为Flag(形式:[IP地址])提交; 解析:http.request.method==POST Flag:[172.16.1.102] 2.继续…...
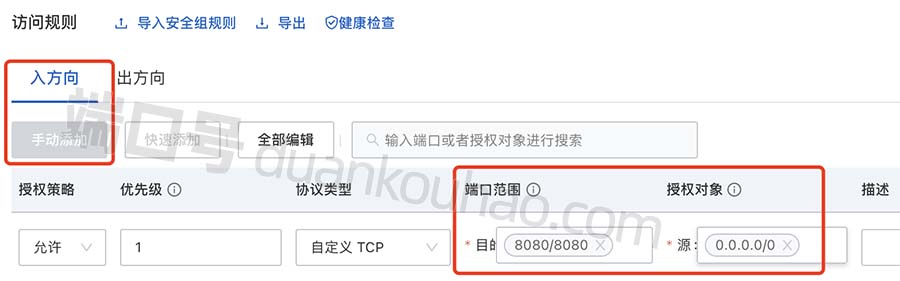
阿里云服务器8080端口安全组开通图文教程
阿里云服务器8080端口开放在安全组中放行,Tomcat默认使用8080端口,8080端口也用于www代理服务,阿腾云atengyun.com以8080端口为例来详细说下阿里云服务器8080端口开启教程教程: 阿里云服务器8080端口开启教程 阿里云服务器8080端…...
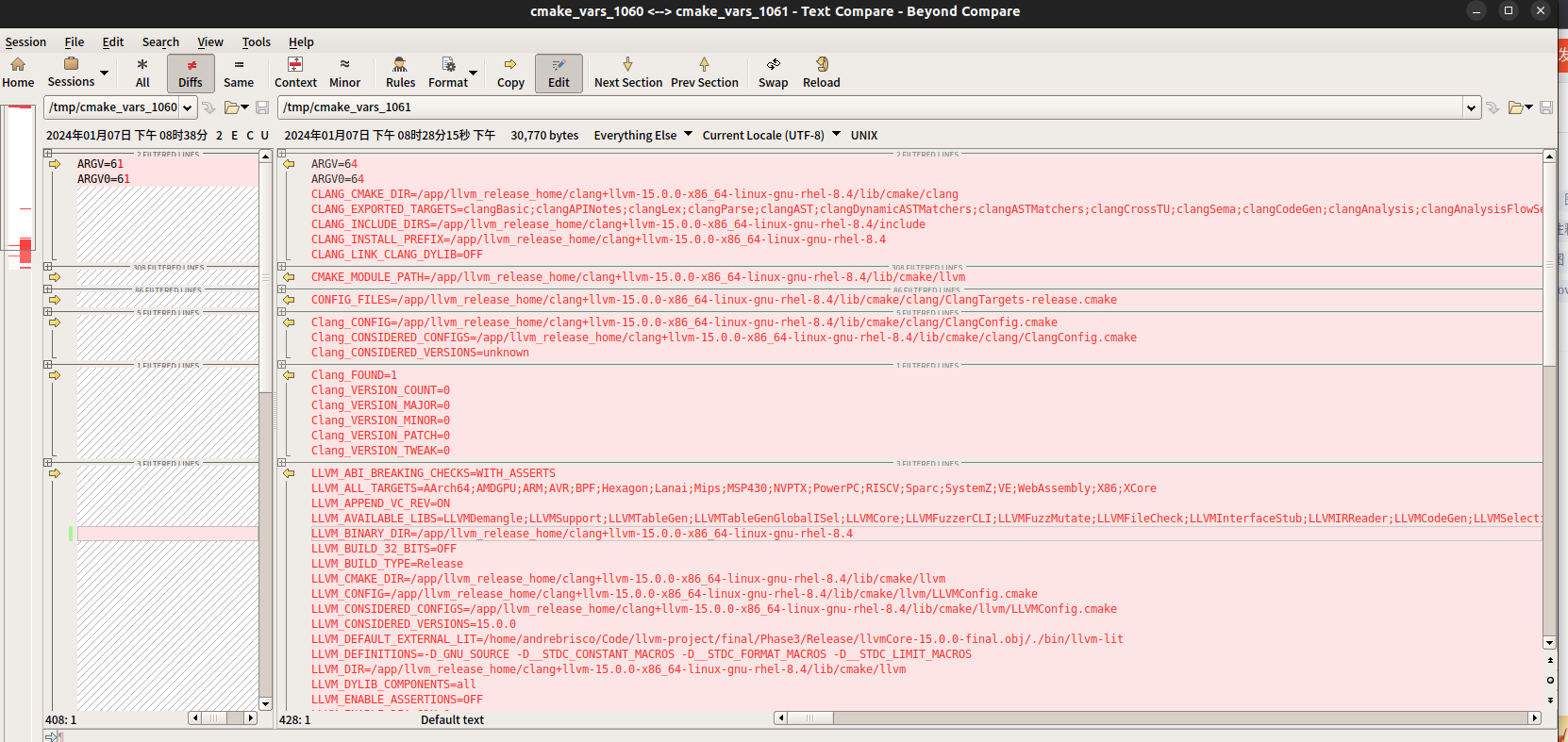
vmlinux, vmlinux.bin, bzImage; cmake的find_package(Clang)新增了哪些变量( 比较两次记录的所有变量差异)
vmlinux, vmlinux.bin, bzImage cd /bal/linux-stable/ file vmlinux #vmlinux: ELF 32-bit LSB executable, Intel 80386, version 1 (SYSV), statically linked, BuildID[sha1]=b99bbd9dda1ec2751da246d4a7ae4e6fcf7d789b, not stripped #文件大小 20MB, 19940148Bfile ar…...

webpack配置入门
webpack是需要一定配置才能使用的,否则无任何效果。在开始webpack学习之前必须理解以下5个核心概念。 5大核心配置 1.entry(入口) webpack从那个文件开始打包,支持单文件入口(vue和react脚手架单入口)和多文件入口 2.output(输…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...
