OpenCV-Python(25):Hough直线变换
目标
- 理解霍夫变换的概念
- 学习如何在一张图片中检测直线
- 学习函数cv2.HoughLines()和cv2.HoughLinesP()
原理
霍夫变换在检测各种形状的的技术中非常流行。如果你要检测的形状可以用数学表达式写出来,你就可以是使用霍夫变换检测它。即使检测的形状存在一点破坏或者扭曲也可以使用。我们下面就看看如何使用霍夫变换检测直线。
一条直线可以用数学表达式y = mx + c 或者ρ = x cos θ + y sin θ 表示。ρ 是从原点到直线的垂直距离,θ 是直线的垂线与横轴顺时针方向的夹(如果你使用的坐标系不同方向也可能不同,我是按OpenCV 使用的坐标系描述的)。如下图所示:

所以如果一条线在原点下方经过,ρ 的值就应该大于0度小于180。但是如果从原点上方经过的话,角度不是大于180也是小于180,但ρ 的值小于0。垂直的线角度为0 度,水平线的角度为90 度。
让我们来看看霍夫变换是如何工作的。每一条直线都可以用(ρ, θ) 表示。所以我们先创建一个2D 数组(累加器),初始化累加器,所有的值都为0。行表示ρ,列表示θ。这个数组的大小决定了最后结果的准确性。如果你希望角度精确到1 度,你就需要180 列。对于ρ,最大值为图片对角线的距离。所以如果精确度要到一个像素的级别,行数就应该与图像对角线的距离相等。
想象一下我们有一个大小为100x100 的直线位于图像的中央。取直线上的第一个点,我们知道此处的(x,y)值。把x 和y 带入上面的方程组,然后遍历θ 的取值:0、1、2、3、. . .180。分别求出与其对应的ρ 的值,这样我们就得到一系列(ρ, θ)的数值对,如果这个数值对在累加器中也存在相应的位置对,就在这个位置上加1。所以现在累加器中的(50,90)=1。(一个点可能存在与多条直线中,所以对于直线上的每一个点可能是累加器中的多个值同时加1)。
现在取直线上的第二个点。重复上面的过程。更新累加器中的值。现在累加器中(50,90)的值为2。你每次做的就是更新累加器中的值。对直线上的每个点都执行上面的操作,每次操作完成之后,累加器中的值就加1,但其他地方有时会加1, 有时不会。按照这种方式下去得到最后累加器中(50,90)的值肯定是最大的。如果你搜索累加器中的最大值,并找到其位置(50,90)就说明图像中有一条直线,这条直线到原点的距离为50,它的垂线与横轴的夹角为90 度。下面的动画很好的演示了这个过程。
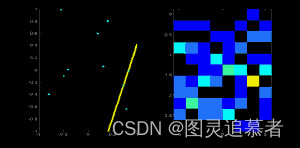
这就是霍夫直线变换工作的方式。下图显示了一个累加器。其中最亮的两个点代表了图像中两条直线的参数 。

OpenCV中的霍夫变换
上面介绍的整个过程原理在OpenCV 中被封装成一个函数cv2.HoughLines()。该函数是OpenCV中用于检测图像中直线的函数,它是基于霍夫变换的一种实现。
函数原型如下:
lines = cv2.HoughLines(image, rho, theta, threshold[, lines[, srn[, stn[, min_theta[, max_theta]]]]])
参数说明:
image:输入图像,通常为二值图像(边缘检测后的图像)。rho:距离分辨率,表示以像素为单位的距离精度。theta:角度分辨率,表示以弧度为单位的角度精度。threshold:累加器阈值,表示直线被检测到所需的最小投票数,高于该值时才被认为是一条直线,也可以把它看成能检测到的直线的最短长度,以像素点为单位。lines:可选参数,用于存储检测到的直线的输出数组。srn:可选参数,表示距离rho的累加器的分割数。stn:可选参数,表示角度theta的累加器的分割数。min_theta:可选参数,表示直线角度的最小值。max_theta:可选参数,表示直线角度的最大值。
函数返回值:
lines:检测到的直线的数组,每个直线由rho和theta表示。
cv2.HoughLines()函数会在输入图像中应用霍夫变换来检测直线,然后返回检测到的直线的rho和theta值。这些直线可以通过在输入图像上进行绘制来可视化。
import cv2
import numpy as np# 加载图像
image = cv2.imread('image.jpg')
# 灰度转换
gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)# 边缘检测
edges = cv2.Canny(gray, 50, 150, apertureSize=3)# 执行霍夫直线变换
lines = cv2.HoughLines(edges, 1, np.pi/180, 200)# 绘制检测到的直线
if lines is not None:for rho, theta in lines[0]:a = np.cos(theta)b = np.sin(theta)x0 = a * rhoy0 = b * rhox1 = int(x0 + 1000 * (-b))y1 = int(y0 + 1000 * (a))x2 = int(x0 - 1000 * (-b))y2 = int(y0 - 1000 * (a))cv2.line(image, (x1, y1), (x2, y2), (0, 255, 0), 2)# 显示结果
cv2.imshow('Hough Lines', image)
cv2.waitKey(0)
cv2.destroyAllWindows()
在这个示例中,首先加载图像并将其转换为灰度图像。然后使用Canny边缘检测算法检测图像的边缘。接下来,使用cv2.HoughLines函数执行霍夫直线变换,并设置了一些参数,例如距离分辨率、角度分辨率和阈值。最后,根据检测到的直线参数绘制直线,并显示结果图像。
结果如下:

概率霍夫变换(Probabilistic Hough Transform)
从上面的检测过程我们可以发现:仅仅是一条直线都需要两个参数,这需要大量的计算。Probabilistic_Hough_Transform 是对霍夫变换的一种优化。它不会对每一个点都进行计算,而是从一幅图像中随机选取(是不是也可以使用图像金字塔呢,一个点集计算对于直线检测来说已经足够了。但是使用这种变换我们必须降低低阈值,因为总的点数变少了阈值值肯定也要小呀。下图是对两种方法的对比。

OpenCV 中使用的Matas, J. Galambos, C. 和Kittler, J.V. 提出的Progressive Probabilistic Hough Transform。这个函数是cv2.HoughLinesP()。函数原型如下:
lines = cv2.HoughLinesP(image, rho, theta, threshold[, lines[, minLineLength[, maxLineGap]]])
参数说明:
image:输入图像,通常为二值图像(边缘检测后的图像)。rho:距离分辨率,表示以像素为单位的距离精度。theta:角度分辨率,表示以弧度为单位的角度精度。threshold:累加器阈值,表示直线被检测到所需的最小投票数。lines:可选参数,用于存储检测到的直线的输出数组。minLineLength:可选参数,表示直线的最小长度阈值,比这个短的都会忽略。maxLineGap:可选参数,表示直线上的最大间隙,小于此值得看做是直线。
函数返回值:
lines:检测到的直线的数组,每个直线由起点和终点表示。
cv2.HoughLinesP()函数会在输入图像中应用霍夫变换来检测直线,然后返回检测到的直线的起点和终点坐标,这些直线可以通过在输入图像上进行绘制来可视化,而在前面的例子中,我们只得到了直线的参数,而且你必须找到所有的直线。而在这里一切变得很直接很简单。
import cv2
import numpy as npimg = cv2.imread('dave.jpg')
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
edges = cv2.Canny(gray,50,150,apertureSize = 3)minLineLength = 100
maxLineGap = 10lines = cv2.HoughLinesP(edges,1,np.pi/180,100,minLineLength,maxLineGap)for x1,y1,x2,y2 in lines[0]:cv2.line(img,(x1,y1),(x2,y2),(0,255,0),2)
cv2.imwrite('houghlines5.jpg',img)结果如下:

相关文章:

OpenCV-Python(25):Hough直线变换
目标 理解霍夫变换的概念学习如何在一张图片中检测直线学习函数cv2.HoughLines()和cv2.HoughLinesP() 原理 霍夫变换在检测各种形状的的技术中非常流行。如果你要检测的形状可以用数学表达式写出来,你就可以是使用霍夫变换检测它。即使检测的形状存在一点破坏或者…...
--状态码详解对照表(详解))
python接口自动化(七)--状态码详解对照表(详解)
1.简介 我们为啥要了解状态码,从它的作用,就不言而喻了。如果不了解,我们就会像个无头苍蝇,横冲直撞。遇到问题也不知道从何处入手,就是想找别人帮忙,也不知道是找前端还是后端的工程师。 状态码的作用是&a…...

Android 实现动态申请各项权限
在Android应用中,如果需要使用一些敏感的权限(例如相机、位置等),需要经过用户的授权才能访问。在Android 6.0(API级别23)及以上的版本中,引入了动态权限申请机制。以下是在Android应用中实现动…...
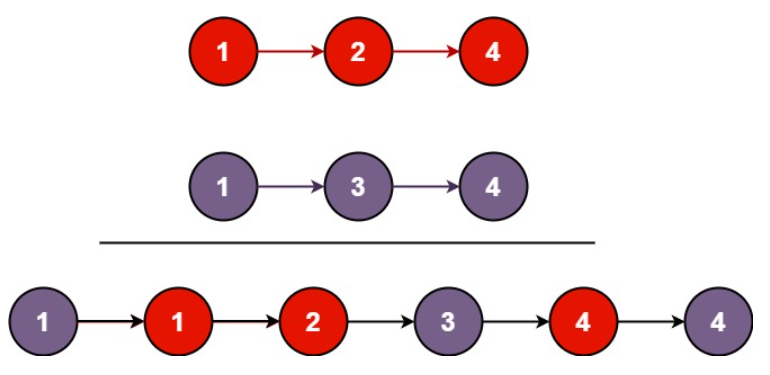
【leetcode】力扣热门之合并两个有序列表【简单难度】
题目描述 将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。 用例 输入:l1 [1,2,4], l2 [1,3,4] 输出:[1,1,2,3,4,4] 输入:l1 [], l2 [] 输出:[] 输入:l1 []…...
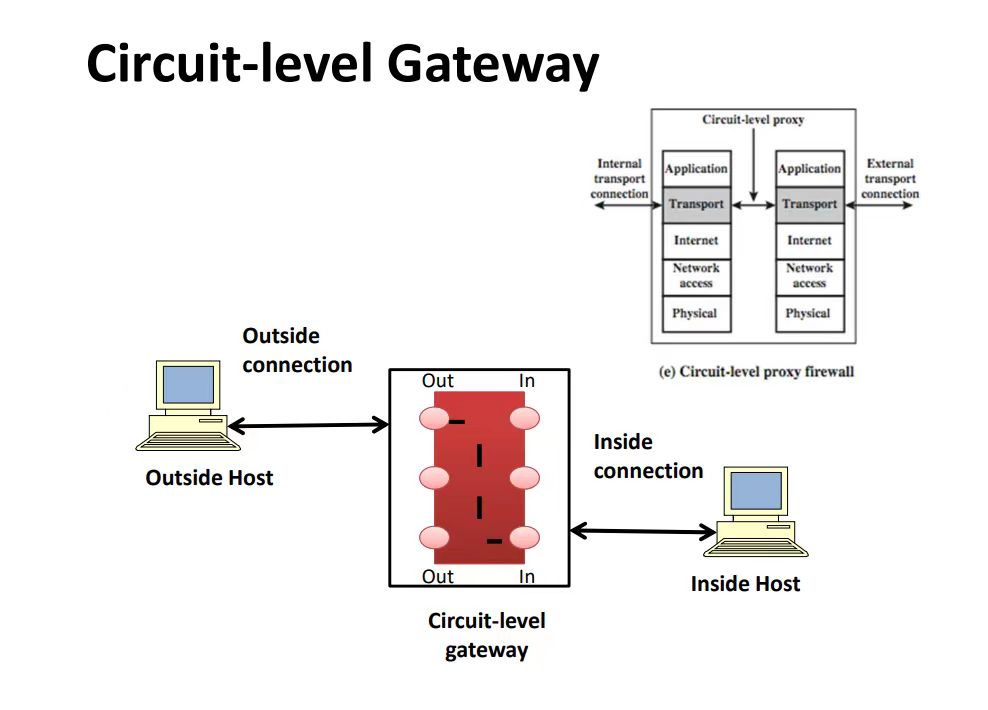
安全与认证Week3 Tutorial+历年题补充
目录 1) 什么是重放攻击? 2)什么是Kerberos系统?它提供什么安全服务? 3)服务器验证客户端身份的一种简单方法是要求提供密码。在Kerberos中不使用这种身份验证,为什么?Kerberos如何对服务器和客户机进行身份验证? 4) Kerberos的四个要求是什么?Kerberos系…...

【Kotlin】协程
Kotlin协程 背景定义实践GlobalScope.launchrunBlocking业务实践 背景 在项目实践过程中,笔者发现很多异步或者耗时的操作,都使用了Kotlin中的协程,所以特地研究了一番。 定义 关于协程(Coroutine),其实…...

Scikit-Learn线性回归(五)
Scikit-Learn线性回归五:岭回归与Lasso回归 1、误差与模型复杂度2、范数与正则化2.1、范数2.2、正则化3、Scikit-Learn Ridge回归(岭回归)4、Scikit-Learn Lasso回归1、误差与模型复杂度 在第二篇文章 Scikit-Learn线性回归(二) 中,我们已经给出了过拟合与模型泛化的概念并…...

React(2): 使用 html2canvas 生成图片
使用 html2canvas 生成图片 需求 将所需的内容生成图片div 中包括 svg 等 前置准备 "react": "^18.2.0","react-dom": "^18.2.0","html2canvas": "^1.4.1",实现 <div ref{payRef}></div>const pa…...

CAN物理层协议介绍
目录 编辑 1. CAN协议简介 2. CAN物理层 3. 通讯节点 4. 差分信号 5. CAN协议中的差分信号 1. CAN协议简介 CAN是控制器局域网络(Controller Area Network)的简称,它是由研发和生产汽车电子产品著称的德国BOSCH公司开发的,并最终成为国际标准(ISO11519) ࿰…...
)
华为OD机试真题-计算面积-2023年OD统一考试(C卷)
题目描述: 绘图机器的绘图笔初始位置在原点(0, 0),机器启动后其绘图笔按下面规则绘制直线: 1)尝试沿着横向坐标轴正向绘制直线,直到给定的终点值E。 2)期间可通过指令在纵坐标轴方向进行偏移,并同时绘制直线,偏移后按规则1 绘制直线;指令的格式为X offsetY,表示在横…...
设计模式之策略模式【行为型模式】
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档> 学习的最大理由是想摆脱平庸,早一天就多一份人生的精彩;迟一天就多一天平庸的困扰。各位小伙伴,如果您: 想系统/深入学习某…...

git使用(完整流程)
1. 新建仓库 1.右击 git bash 后 输入 git init (仓库为:当前目录) git init name (仓库为:name文件夹) git clone https://github.com/Winnie996/calculate.git //https2.工作区域 工作目录 3. 添加 提交 git add . //工作区添加至暂存区 git commit -m "注释内容&q…...
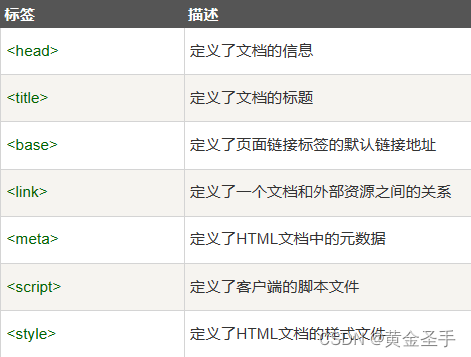
九、HTML头部<head>
一、HTML头部<head> 1、<title>- 定义了HTML文档的标题 使用 <title> 标签定义HTML文档的标题 <!DOCTYPE html> <html><head><meta charset"utf-8"><title>我的 HTML 的第一页</title> </head><b…...
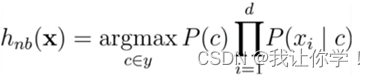
机器学习期末复习
机器学习 选择题名词解释:简答题计算题一、线性回归二、决策树三、贝叶斯 选择题 机器学习利用经验 ,须对以下()进行分析 A 天气 B 数据 C 生活 D 语言 归纳偏好值指机器学习算法在学习的过程中,对以下(&a…...

python-日志模块以及实际使用设计
python-日志模块以及实际使用设计 1. 基本组成 日志模块四个组成部分: 日志对象:产生日志信息日志处理器:将日志信息输出到指定地方,例如终端、文件。格式器:在日志处理器输出之前,对信息进行各方面的美化…...
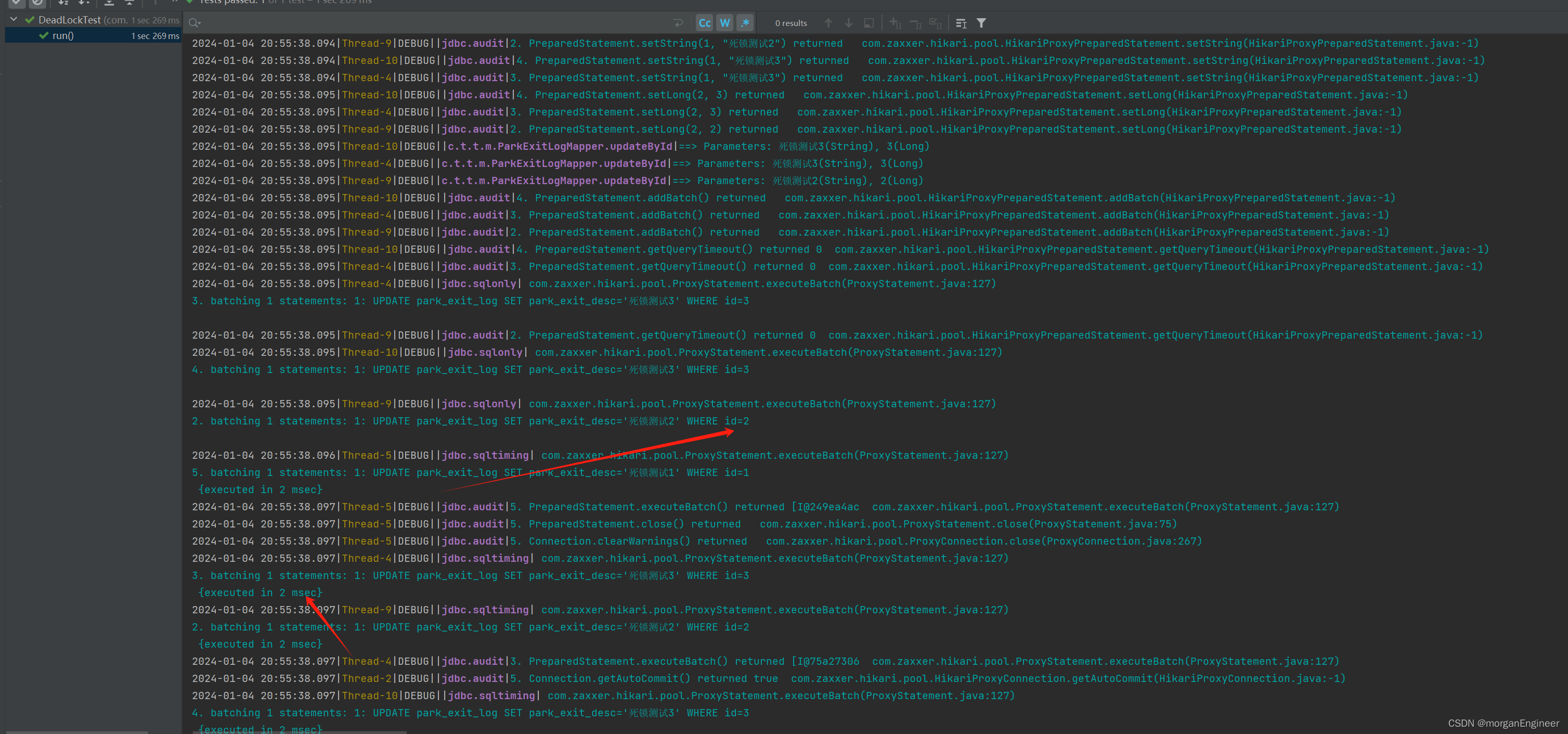
googlecode.log4jdbc慢sql日志,格式化sql
前言 无论使用原生JDBC、mybatis还是hibernate,使用log4j等日志框架可以看到生成的SQL,但是占位符和参数总是分开打印的,不便于分析,显示如下的效果: googlecode Log4jdbc 是一个开源 SQL 日志组件,它使用代理模式实…...
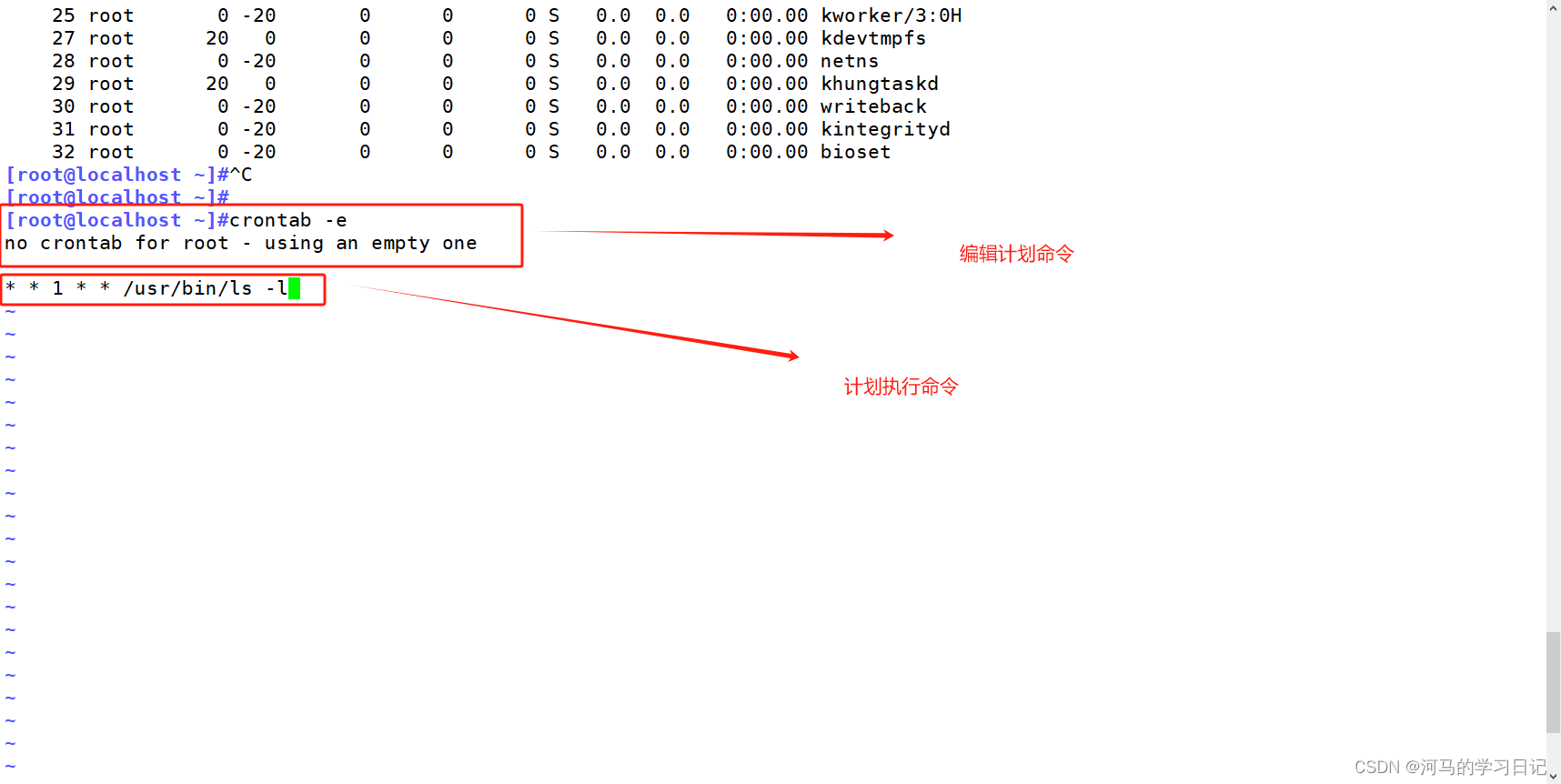
Linux程序、进程和计划任务
目录 一.程序和进程 1.程序的概念 2.进程的概念 3.线程的概念 4.单线程与多线程 5.进程的状态 二.查看进程信息相关命令: 1.ps:查看静态进程信息状态 2.top:查看动态进程排名信息 3.pgrep:查看指定进程 4.pstree&#…...

【MySQL】索引基础
文章目录 1. 索引介绍2. 创建索引 create index…on…2.1 explain2.2 创建索引create index … on…2.3 删除索引 drop index … on 表名 3. 查看索引 show indexes in …4. 前缀索引4.1 确定最佳前缀长度:索引的选择性 5. 全文索引5.1 创建全文索引 create fulltex…...

精确管理Python项目依赖:自动生成requirements.txt的智能方法
在Python中,可以使用几种方法来自动生成requirements.txt文件。这个文件通常用于列出项目所需的所有依赖包及其版本,使其他人或系统可以轻松地重现相同的环境。下面是几种常见的方法: 使用pip freeze: 这是最常见的方法。pip free…...
JavaWeb基础(1)- Html与JavaScript(JavaScript基础语法、变量、数据类型、运算符、函数、对象、事件监听、正则表达式)
JavaWeb基础(1)- Html与JavaScript(JavaScript基础语法、变量、数据类型、运算符、函数、对象、事件监听、正则表达式) 文章目录 JavaWeb基础(1)- Html与JavaScript(JavaScript基础语法、变量、数据类型、运算符、函数、对象、事件…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...
