leetcode动态规划问题总结 Python
目录
一、基础理论
二、例题
1. 青蛙跳台阶
2. 解密数字
3. 最长不含重复字符的子字符串
4. 连续子数组的最大和
5. 最长递增子序列
6. 最长回文字符串
7. 机器人路径条数
8. 礼物的最大价值
一、基础理论
动态规划其实是一种空间换时间的基于历史数据的递推算法,甚至有时连空间也可以节省。动态规划算法,需要 3 个步骤。第一步决定用于记录历史计算结果的数据结构,例如 dp[];第二步构建递推公式,例如 dp[n]=dp[n-1]+dp[n-2];第三步设定初始值和递推顺序,例如 dp[0]=0, dp[1]=1。
二、例题
1. 青蛙跳台阶
一只青蛙一次可以跳上 1 级台阶,也可以跳上 2 级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。
示例:
输入:3
输出:3
本题首先使用 dp[i] 数据结构存储中间结算结果,表示 i 级台阶的跳法数量,由于要想跳到第 i 级台阶只能从第 i-1 级或者 i-2级台阶跳过来,所以递推公式为 dp[i] = dp[i-1] + dp[i-2],由于想要跳到第 1 级台阶只有一种跳法,要跳到第 2 级台阶有两种跳法,所以初始值 dp[1]=1, dp[2]=2。
def jumpFloor(n):if (n <= 2):return ndp = [0]*(n+1) # 创建一个数组来保存历史数据,多补了一个用不到的0位dp[1] = 1 # 给出初始值dp[2] = 2for i in range(3, n+1): # 通过关系式来计算dp[n]dp[i] = dp[i-1] + dp[i-2]return dp[n]该问题还可以进一步扩展为:一只青蛙一次可跳上 1 级台阶,也可以跳上 2 级 … 它也可以跳上 n 级。求该青蛙跳上一个n级的台阶(n 为正整数)总共有多少种跳法。
扩展问题无法用动态规划来解,需要通过分析得到公式,具体为:
f(n) = f(n-1) + f(n-2) + f(n-3) +… f(1)
f(n-1) = f(n-2) + f(n-3) +… f(1)
f(n) = 2*f(n-1) n>1
2. 解密数字
现有一串神秘的密文 ciphertext,经调查,密文的特点和规则如下:
密文由非负整数组成,数字 0-25 分别对应字母 a-z
请根据上述规则将密文 ciphertext 解密为字母,并返回共有多少种解密结果。
示例:
输入: ciphertext = 216612
输出: 6
解释: 216612 解密后有 6 种不同的形式,分别是 "cbggbc","vggbc","vggm","cbggm","cqggbc" 和 "cqggm"
本题首先使用 dp[i] 表示长度为 i 的字符串的解法,然后分析递推公式。如果第 i-1 数字为 0,那 dp[i] == dp[i-1];如果第 i-1 数字为 1,那 dp[i] == dp[i-1] + dp[i-2];如果第 i-1 数字为 2,且第 i 数字小于 6,那 dp[i] == dp[i-1] + dp[i-2];如果第 i-1 数字大于 2,那 dp[i] == dp[i-1]。所以只需要 i-1 和 i 数字组成的数字大于等于 10 小于等于 25,则 dp[i] == dp[i-1] + dp[i-2],否则 dp[i] == dp[i-1]。需要注意,在使用 dp 时,我们在前面补一个用不到的 0,这样做的目的是让索引 i 与实际长度匹配,但是当需要访问 s 时需要注意 dp[i] 与 s[i-1] 对应。一定要理清楚 dp 与 s 的索引之间的关系,否则很容易搞混了。
def translateNum(num):s = str(num)dp = [1] * (len(s)+1) # 定义状态列表,在0位置添加了一个1,以便于递推公式的进行,以及索引与实际长度匹配dp[1] = 1 # 长度1时的解法for i in range(2, len(s)+1): # 长度2到长度n的解法if int(s[i-2:i]) >9 and int(s[i-2:i]) < 26: # dp[i]对应s[i-1]索引dp[i] = dp[i-1] + dp[i-2]else:dp[i] = dp[i-1]return dp[-1]3. 最长不含重复字符的子字符串
请从字符串中找出一个最长的不包含重复字符的子字符串,计算该最长子字符串的长度。
示例 :
输入: "abcabcbb"
输出: 3 解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
该问题首先使用 dp[i] 表示以 s[i] 为结点的最长不包含重复字符的字符串长度,最终结果就是 dp 中的最大值。那递推公式很容易想到,如果 s[i] 不存在于以 s[i-1] 为结点的最长不包含重复字符的字符串中,那么 dp[i] = dp[i-1] + 1;如果s[i] 存在于以 s[i-1] 为结点的最长不包含重复字符的字符串中,且重复字符所在索引是 j,那么 dp[i] = i - j。此时引出一个问题,如何获取这个字符串,如何判断一个字符是否存在于这个字符串中,以及如何获取重复字符的索引,这个还是非常困难的。所以这里采用另外一种办法,可以使用字典数据结构把所有的字符和索引均存储起来,键是字符,值是索引,当字符存在重复时,会被覆盖,所以通过这个字典可以获取 s[j] 左侧是否存在重复字符,如果存在可以获得最近的索引,如果不存在可以使用默认值 -1 表示,那么此时就可以通过 i-j 与 dp[i-1] + 1 的大小比较以判断是否存在重复字符了,但这种办法会增加内存使用量。这里初始值 dp[0] = 1。
def lengthOfLongestSubstring(s): # 本函数有很多优化点,但为了便于理解,这里没有优化if not s: return 0 # 如果为空,则返回 0 || 可优化掉dic = {} # 定义哈希表,用于获取最近相同字符的索引dic[s[0]] = 0 # 初始化第一个字符对应的哈希表 || 可优化掉,直接放进循环里dp = [1] * len(s) # 初始化第一个字符对应的 dp || 可优化掉,直接使用一个变量值记录res = 1 # 初始化第一个字符的 res 结果for i in range(1, len(s)): # 从第二个字符开始处理j = dic.get(s[i], -1) # 获取 s[i] 左侧最近相同元素的索引 jif dp[i-1] + 1 < i - j: # 如果 i-j 大于 dp[i-1]+1 说明在 s[j] 并不存在于以 s[j-1] 为结点的最长无重复字符串中 || 可优化为min()函数dp[i] = dp[i-1] + 1else: # 反之dp[i] = i - jdic[s[i]] = i # 哈希表记录每个字符,这会造成内存使用量偏高res = max(res, dp[i])return res针对本问题,这里还有一个思路,即实时维护一个集合,当向右遍历字符串时,使得集合中的元素使用对应着当前的最长无重复字符串。那此时就需要一个左指针 left 和一个右指针 i,以及需要实时维护的集合 lookup。i 需要向右遍历,所以 i 对应一个 for 循环。每遍历一个 i 值,需要首先删除集合 lookup 中与 s[i] 重复的字符左侧的所有字符,这里使用了一个很巧妙的办法,即从 left 开始一直删除,直至不存在重复。最后需要将当前字符 s[i] 放入集合中,以完成针对 i 的遍历。此方案在空间消耗上要优于方案1。
def lengthOfLongestSubstring(s):if not s:return 0left = 0 # 左指针lookup = set() # 字典max_len = 0cur_len = 0for i in range(len(s)): # i是右指针,每遍历一个i,lookup都是由left到i的元素组成的字典cur_len += 1while s[i] in lookup: # 每遍历一个i,删除lookup中的重复元素,并同步修改leftlookup.remove(s[left])left += 1cur_len -= 1 # 附带着同步修改当前i对应字符串的长度if cur_len > max_len:max_len = cur_lenlookup.add(s[i])return max_len4. 连续子数组的最大和
输入一个长度为 n 的整型数组 array,数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。
示例:
输入:[1,-2,3,10,-4,7,2,-5]
输出:18
该问题取 dp[i] 作为以 s[i] 为结尾的连续子数组的最大和,那 max(dp) 为最终结果。递推公式为 if dp[i-1]>0: dp[i]=dp[i-1]+s[i] else: dp[i]=s[i]。
def maxSubArray(nums):dp = [nums[0]] * len(nums)for i in range(1, len(nums)):if dp[i-1] > 0:dp[i] = dp[i-1] + nums[i]else:dp[i] = nums[i]return max(dp)如果不仅想要获取最大和,还需要获取最大和所对应的字符串,那就需要增加几个变量实时记录当前 dp[i] 所对应的字符串,这里其实属于滑动窗口问题了,滑动窗口的右边界很容易界定,就是遍历的参数,左边界不太好想清楚,其实左边界只有在 dp[i-1] 小于 0 的时候才会更新,且更新为 i,想明白了这一点,那就好编程了。
def maxSubArray(nums):dp = [nums[0]] * len(nums)max_value = nums[0]beign = 0end = 0max_beign = 0max_end = 0for i in range(1, len(nums)):if dp[i-1] > 0:dp[i] = dp[i-1] + nums[i]else:dp[i] = nums[i]beign = i # 这个是最关键的点,需要想清楚end = iif dp[i] > max_value:max_value = dp[i]max_beign = beignmax_end = endreturn (max_value, nums[max_beign:max_end+1])5. 最长递增子序列
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
示例:
输入:nums = [10,9,2,5,3,7,101,18]
输出:4 解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
该问题选用 dp 作为中间数据存储结构,以 dp[i] 表示以 s[i] 为结尾的最大递增子序列长度。接下来是递推公式,首先想到的是与 dp[i-1] 之间的关系,但是这次的子序列是允许跳跃的,所以不一定只是与 dp[i-1] 之间有关系,所以仔细想清楚后,发现 dp[i] 其实与 dp[0]...dp[i-1] 都有关系,需要找出来的是在 s[i]>s[index] 前提下找到 max(dp[index]...)。
def lengthOfLIS(nums):dp = [1]*len(nums)for i in range(len(nums)):for j in range(i):if nums[i] > nums[j]:dp[i] = max(dp[i], dp[j]+1)return max(dp)如果想要同步获取这个子序列,那需要定义一个变量 result 保存所有的最长递增子序列,reslut[i] 存储的是以 s[i] 为结尾的最长递增子序列。然后在更新 dp 的时候同步更新 result。这里需要特别注意的是 [[]]*len(nums) 的方式属于浅拷贝,更新任何一个 [] 都会同步影响其它 []。在做 List 的整体赋值时一定注意好是需要赋值、浅拷贝还是深拷贝。深拷贝可以使用 copy 包或者 [:] 运算符。
import copydef lengthOfLIS(nums):dp = [1]*len(nums)max_dp = 1max_i = 0# results = [[]]*len(nums) # 不能这样写,这是浅拷贝results = [[] for _ in range(len(nums))] # 记录以s[i]结尾的最长递增子序列for i in range(len(nums)):for j in range(i,-1,-1): # 检查i之前所有序列if nums[i] > nums[j]: # 前提是s[i]大于s[j]if dp[i] < dp[j] + 1: # 次之是序列长度要更长,因为存在相等的情况,所以存在答案不唯一dp[i] = dp[j] + 1results[i] = copy.deepcopy(results[j]) # 注意这里一定要用深拷贝# results[i] = results[j][:] # 注意这里一定要用深拷贝results[i].append(nums[i])if max_dp < dp[i]:max_dp = dp[i]max_i = ireturn (dp[max_i], results[max_i])6. 最长回文字符串
给你一个字符串 s,找到 s 中最长的回文字符串。
示例 :
输入:s = "babad"
输出:"bab" 解释:"aba" 同样是符合题意的答案。
本题采用二维 dp 作为中间存储数据结构,dp[i,j] 表示 s[i] 到 s[j] 是否为回文字符串,主对角线表示每个单独的字符均为长度 1 的回文字符,如果首尾两个元素相等,中间部分也是回文字符串,那当前字符串也为回文字符串,所以递推公式为 dp[i,j] = dp[i+1,j-1] and s[i]==s[j],从递推公式可以得到遍历输出是 i 从大到小 j 从小到大,至此可以获取任意字符串是否为回文字符串。在遍历的同时记录下最长长度和对应的起止点。
def longest_palindrome(s):dp = [[True]*len(s) for _ in range(len(s))] # 注意深浅拷贝问题,直接相乘属于浅拷贝max_len = 1max_beign = 0max_end = 0for i in range(len(s)-2, -1, -1):for j in range(i+1, len(s)):dp[i][j] = dp[i+1][j-1] and s[i]==s[j]if dp[i][j] and max_len < j-i+1: # 记录最长长度和对应起始终止位置max_len = j-i+1max_beign = imax_end = jreturn (max_len, s[max_beign:max_end+1])本题还可以采用中心扩展法,即定义一个函数可以实现通过两边扩展遍历的方式寻找最长回文字符串,返回回文字符串的长度和起始点,然后遍历所有字符,检查每个字符对应的最长回文字符串,即可获取最长回文字符串。暴力遍历法的时间复杂度是O3,空间复杂度是O1,而动态规划的时间复杂度是O2,空间复杂度是O1,最后中心扩展法的时间复杂度是O2,空间复杂度是O1。
def longest_palindrome(s):def check(s, i, j): # 检查从i和j向两边扩散的字符串是否是回文字符串while i>=0 and j<len(s) and s[i]==s[j]: # 实际仅仅用于 i=j 或者 i=j-1 两种情况i -= 1j += 1return j-i-1, i+1, j-1 # 返回回文字符串的长度和起始以及终止点max_len = 1max_beign = 0max_end = 0for i in range(len(s)):len1, left1, right1 = check(s, i, i)len2, left2, right2 = check(s, i, i+1)if max_len < max(len1, len2):max_len = max(len1, len2)if len1 >= len2:max_beign = left1max_end = right1else:max_beign = left2max_end = right2 return s[max_beign:max_end+1]
7. 机器人路径条数
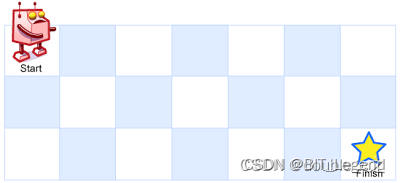
一个机器人位于一个 mxn 网格的左上角(起始点在上图中标记为 “Start” )。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。问总共有多少条不同的路径?
示例:
输入:m=3, n=7
输出:28
本问题需要准备一个二维的 dp 数据结构记录中间过程,dp[i,j] 表示从起点到 (i,j) 位置的路径条数,dp[-1,-1]即为最终结果。那递推公式显然就是 dp[i,j]=dp[i-1,j]+dp[i,j-1]。初始条件,第一行和第一列全部为1,递推顺序是第二行开始从左到右,从上到下。
def uniquePaths(m, n):dp = [[1 for _ in range(n)] for _ in range(m)]for i in range(1, m):for j in range(1, n):dp[i][j] = dp[i - 1][j] + dp[i][j - 1]return dp[-1][-1]8. 礼物的最大价值
在一个 mxn 的棋盘的每一格都放有一个礼物,每个礼物都有一定的价值(价值大于 0)。你可以从棋盘的左上角开始拿格子里的礼物,并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值,请计算你最多能拿到多少价值的礼物?
示例:
输入:[ [1,3,1], [1,5,1], [4,2,1] ]
输出:12 解释: 路径 1→3→5→2→1 可以拿到最多价值的礼物
本问题需要准备一个二维的 dp 数据结构记录中间过程,dp[i,j] 表示从起点到 (i,j) 位置的最多礼物,dp[-1,-1] 即为最终结果。那递推公式显然就是 dp[i,j]=max(dp[i-1,j]+dp[i,j-1])+grid[i,j]。初始条件,第一行和第一列全部为累计求和结果,递推顺序是第二行开始从左到右,从上到下。
def maxValue(grid):m, n = len(grid), len(grid[0])dp = [[grid[0][0] for _ in range(n)] for _ in range(m)]for i in range(1, m):dp[i][0] = dp[i-1][0] + grid[i][0]for j in range(1, n):dp[0][j] = dp[0][j-1] + grid[0][j]for i in range(1, m):for j in range(1, n):dp[i][j] = max(dp[i-1][j], dp[i][j-1]) + grid[i][j]return dp[-1][-1]相关文章:

leetcode动态规划问题总结 Python
目录 一、基础理论 二、例题 1. 青蛙跳台阶 2. 解密数字 3. 最长不含重复字符的子字符串 4. 连续子数组的最大和 5. 最长递增子序列 6. 最长回文字符串 7. 机器人路径条数 8. 礼物的最大价值 一、基础理论 动态规划其实是一种空间换时间的基于历史数据的递推算法&…...

strtok函数的介绍
_str指被分解的字符串 delim指分隔符字符串 返回类型是指针 strtok()用来将字符串分割成一个个片段。参数s指向欲分割的字符串,参数delim则为分割字符串中包含的所有字符。当strtok()在参数s的字符串中发现参数delim中包含的分割字符时,则会将该字符改为\0 字符…...

CF1909_C. Heavy Intervals题解
CF1909_C. Heavy Intervals题解 题目传送门(Problem - C - CodeforcesCodeforces. Programming competitions and contests, programming communityhttps://codeforces.com/contest/1909/problem/C)。 题目翻译如下:(图片来源&a…...

【Python机器学习】理论知识:决策树
决策树是广泛用于分类和回归任务的模型,本质上是从一层层if/else问题中进行学习,并得出结论。这些问题类似于“是不是”中可能问到的问题。 决策树的每个结点代表一个问题或一个包含答案的终结点(叶结点)。树的边奖问题的答案与将…...
天软特色因子看板 (2024.01 第2期)
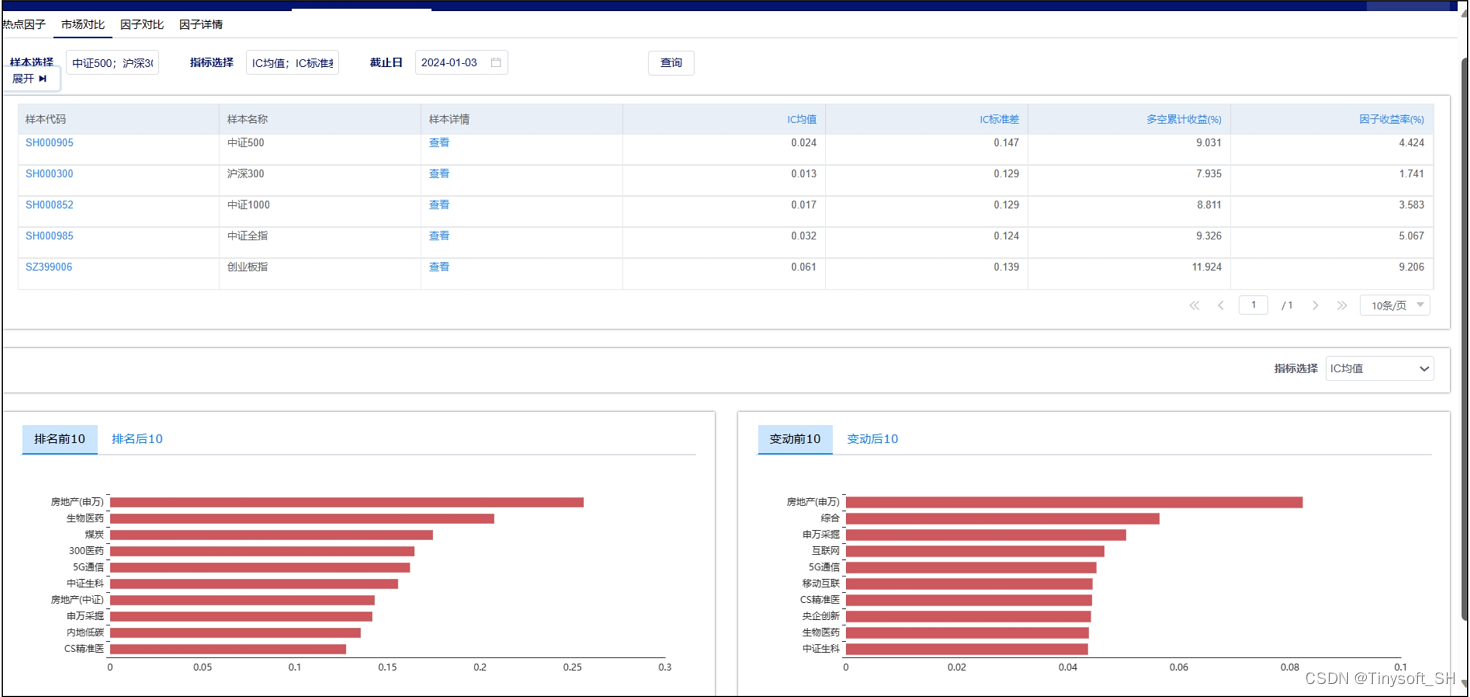
该因子看板跟踪天软特色因子A04001(当日趋势强度),该因子为反映股价走势趋势强弱,用以反映股价走势趋势强弱,abs(值)越接近1,趋势 性越强,符号代表涨跌方向 今日为该因子跟踪第2期,跟踪其在SH000905 (中证5…...
java智慧医院互联网智慧3D导诊系统源码,经由智慧导诊系统多维度计算,准确推荐科室
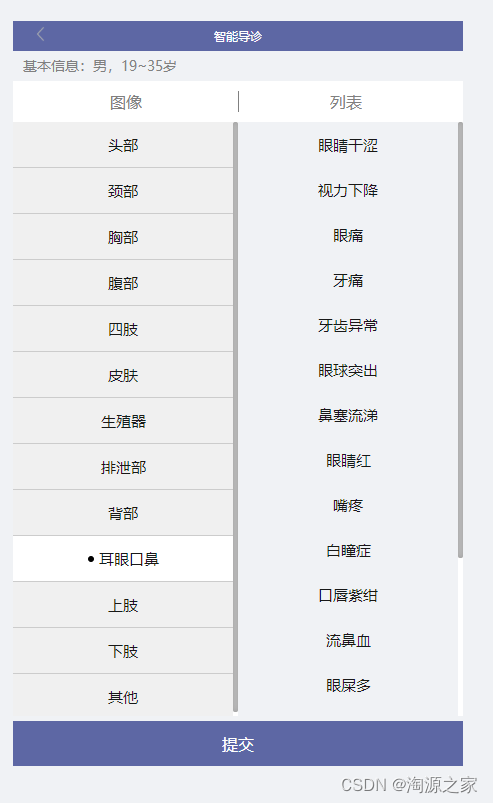
什么是智慧导诊系统? 简单地说,智慧导诊系统是一种利用人工智能技术,为医生提供帮助的系统。它可以通过分析患者的症状和病史为医生提供疾病诊断和治疗方案的建议。 系统介绍: 医院智慧导诊系统是在医院中使用的引导患者自助就诊挂号&…...

WiFi7: MLD寻址
原文:MLD使用MLD MAC address唯一的标识本MLD。 MLD下的STA(s)使用与之不同的MAC address。 NOTE MLD MAC address可以和其下的某个STA的MAC address相同或者不同于任一MAC Address。 原文:对于individually addressed 帧。以下规则适用: Address 2(TA)设置为STA的MAC Add…...
)
laravel-admin之 浏览器自动填充密码(如果需要渲染数据库密码的话,首先确认数据库密码是否可以逆向解密)
参考 https://blog.51cto.com/u_10401840/5180106 为什么浏览器端保存的密码一直自动写入到$form->password 解决办法 2、在页面进入的时候,默认表单的type值为text;推荐指数:2颗星 5、设置表单的readonly属性;推荐指数:4颗…...
jquery图形验证码
效果展示 js图形随机验证码(表单验证) html代码片段 <form class"formwrap"><div class"item"><input type"text" id"code_input" value"" placeholder"请输入验证码"/>…...
dp专题10 目标和
本题链接:. - 力扣(LeetCode) 题目: 思路: 根据这道题,可以通过暴力的方法进行取 号或者 - 号 两个操作,通过当刚好得到 target 的时候 答案 1,但是通过长度是 20 ,操…...

详解 docker 镜像制作的两种方式
概要 制作Docker镜像一般有2种方法: 通过Dockerfile,完成镜像的创建使用仓库中已有的镜像,安装自己使用的软件环境后完成新镜像创建 docker 常用命令 docker build: 用于构建 Docker 镜像。该命令可以从 Dockerfile 构建镜像,…...

selenium元素单击不稳定解决方法
selenium自动化测试过程中,经常会发现某一元素单击,很不稳定,有时候执行了点击没有反映。 以下总结两种解决方法:都是通过js注入的方式去点击。 1.F12查一看,要点击的按钮,或连接,有没有οncl…...

vue3中vite使用sass
引用:https://blog.csdn.net/weiliang_66/article/details/132469597 npm install sass -d配置vite.config.js: css: {preprocessorOptions: {scss: {additionalData:import "/assets/styles/main.scss";}}}创建对应的 main.sass...

centos 8.0 安装sysbench 1.0.17
序号步骤说明执行命令执行结果备注1 下载并解压sysbench-1.0.17.zip sysbench-1.0.17.zip2安装依赖文件 yum install automake libtool -y yum install /usr/include/libpq-fe.h 3安装sysbench cd sysbench-1.0.17 ./autogen.sh ./configure \ --prefix/sysbench \ --with-pgsq…...
LabVIEW开发分布式光纤油气管道泄漏检测及预警系统
LabVIEW开发分布式光纤油气管道泄漏检测及预警系统 随着油气工业的发展,管道泄漏成为一个严峻的安全问题。本文介绍了一种基于LabVIEW的分布式光纤油气管道泄漏检测及预警系统的设计思路和组成结构。系统包括硬件和软件两部分,其中硬件部分详细阐述了分…...
Go后端开发 -- Go Modules
Go后端开发 – Go Modules 文章目录 Go后端开发 -- Go Modules一、什么是Go Modules?二、GOPATH的工作模式1.GOPATH模式2.GOPATH模式的弊端 三、Go Modules模式创建项目1.go mod命令2.go mod环境变量3.使用Go Modules初始化项目4.修改模块的版本依赖关系 四、Go Modules下impo…...
)
基于det_keypoint_unite的ROS功能包(jetson部署)
文章目录 硬件软件FastDeploy编译CMakeLists.txt头文件源代码硬件 Jetson AGX Orin 64GB 软件 gcc/g++ >= 5.4(推荐8.2)cmake >= 3.10.0jetpack >= 4.6.1opencv=4.2.0FastDeploy编译 git clone https://github.com/PaddlePaddle/FastDeploy.git cd FastDeploy mkdi…...

TS 36.211 V12.0.0-下行(8)-调制和上变频
本文的内容主要涉及TS 36.211,版本是C00,也就是V12.0.0。...
基于SSM酒店后台管理系统【源码】【最详细运行文档】
基于SSM酒店后台管理系统【源码】【最详细运行文档】 功能简介技术描述运行准备♝项目运行访问项目 演示图✅源码获取 💡 「分享」 大家好,最近几年在酒店后台管理系统非常流行,无论是上课的项目或者是一些毕设都会以酒店后台管理系统举例说…...

利用Python实现每日新闻早报推送
本文将介绍如何使用Python编写简单的逻辑,通过调用API接口实现每日新闻推送功能。 步骤: 导入所需的库: 在代码的开头,我们需要导入所需的库。通常,我们会使用requests库来发送HTTP请求,以获取新闻数据。 …...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...

Java 与 MySQL 性能优化:MySQL 慢 SQL 诊断与分析方法详解
文章目录 一、开启慢查询日志,定位耗时SQL1.1 查看慢查询日志是否开启1.2 临时开启慢查询日志1.3 永久开启慢查询日志1.4 分析慢查询日志 二、使用EXPLAIN分析SQL执行计划2.1 EXPLAIN的基本使用2.2 EXPLAIN分析案例2.3 根据EXPLAIN结果优化SQL 三、使用SHOW PROFILE…...

海云安高敏捷信创白盒SCAP入选《中国网络安全细分领域产品名录》
近日,嘶吼安全产业研究院发布《中国网络安全细分领域产品名录》,海云安高敏捷信创白盒(SCAP)成功入选软件供应链安全领域产品名录。 在数字化转型加速的今天,网络安全已成为企业生存与发展的核心基石,为了解…...
