【数据库原理】(16)关系数据理论的函数依赖
一.函数依赖的概念
函数依赖是关系数据库中核心的概念,它指的是在属性集之间存在的一种特定的关系。这种关系表明,一个属性集的值可以唯一确定另一个属性集的值。
- 属性子集:在关系模式中,X和Y可以是单个属性,也可以是属性的组合。
- 唯一确定:对于关系模式中的任意两个元组,如果它们在X上的值相同,则它们在Y上的值也必须相同。
定义
- 基本定义:函数依赖,记作
X -> Y,意味着在关系模式R(U)中,如果X是U的子集,那么X的值可以唯一确定Y的值。 - 非平凡函数依赖:如果
Y不是X的子集,则X -> Y是非平凡函数依赖。 - 平凡函数依赖:如果
Y是X的子集,则X -> Y是平凡函数依赖。
完全与部分函数依赖
- 完全函数依赖:如果没有
X的任何真子集能决定Y,则称Y对X完全函数依赖。 - 部分函数依赖:如果
X的某个真子集可以决定Y,则称Y对X部分函数依赖。
传递函数依赖
- 定义:如果
X -> Y和Y -> Z且Y不函数依赖于X,则称Z对X传递函数依赖。。
函数依赖的闭包
- 闭包:由函数依赖集
F推导出的所有函数依赖的集合称为F的闭包,记作 F + F^+ F+。
数据库设计中的应用
- 消除冗余和异常:理解和应用函数依赖有助于减少数据存储中的冗余,并避免更新、插入和删除异常。
- 规范化:函数依赖是数据库规范化过程的基础。通过规范化,可以将数据库分解成多个结构简单、相互独立的小表,从而提高数据库的运行效率和数据的一致性。
实例分析
以一个简单的员工数据库为例,假设有一个关系模式Employee(员工号, 姓名, 部门),其中:
- 如果一个员工号唯一地决定一个员工的姓名和部门,则称姓名和部门函数依赖于员工号(员工号 → 姓名, 部门)。
- 如果部门中的每个员工都有一个唯一的员工号,则员工号函数依赖于部门(部门 → 员工号),这可能表明设计上的问题,因为部门通常包含多个员工。
二.关键字(码)
关键字(码)的定义
- 基本概念:在关系数据库中,关键字(又称码)是一种特殊的属性或属性组合,能够在关系模式中唯一标识每个元组。
- 候选码:关系中所有可能作为唯一标识符的属性集称为候选码。
- 主码:从候选码中选定的一个作为主要的唯一标识符。
- 主属性:包含在任何一个候选码中的属性。
- 非主属性:不包含在任何码中的属性。
关键字的重要性
- 唯一性标识:关键字确保关系中的每个元组都是唯一的,从而使数据的检索和操作更为准确。
- 实体完整性:关键字强制执行实体完整性规则,确保数据库的准确性和可靠性。
- 构建关系:关键字是关系间联系的基础,特别是在实现外键(外部码)时,它们建立了表之间的联系。
主键与外键
- 主键(Primary Key):选定的候选码,用于唯一标识关系中的每个元组。
- 外键(Foreign Key):存在于一个关系中但作为另一个关系的主键的属性或属性组。
示例
假设有关系模式 R(城市, 街道, 邮编),其中 城市 和 街道 的组合能唯一确定一个邮编,这组属性可以作为候选码。如果在另一个关系模式中 邮编 是唯一标识符,则它在当前关系模式中作为外键存在。
选择合适的关键字
在数据库设计中,选择合适的关键字至关重要,因为它影响数据的整合性、存取效率和系统的可维护性。选择时应考虑以下因素:
- 最小化:候选码应该尽可能小,以减少存储空间和提高处理效率。
- 稳定性:选择不易改变的属性作为关键字。
- 简洁性:简单的属性或属性组合更易于管理和使用。
二.Armstrong 公理系统
Armstrong 公理系统为函数依赖的理论提供了一套形式化的推理规则,用于从已知的函数依赖中导出更多的函数依赖。这一系统是关系模式分解算法的理论基础,帮助数据库设计者理解和应用函数依赖的概念。
Armstrong 公理系统的规则
-
自反律 (Reflexivity):
- 如果 Y⊆X⊆U,则 X→Y 是成立的。
- 说明: 任何属性集总是函数决定其子集。
-
增广律 (Augmentation):
- 如果 X→Y 成立,且 Z⊆U,则 XZ→YZ 也成立。
- 说明: 可以在函数依赖的两边同时增加相同的属性集。
-
传递律 (Transitivity):
- 如果 X→Y 和 Y→Z 成立,则 X→Z 也成立。
- 说明: 函数依赖具有传递性。
由于关系的性质,Armstrong 公理系统是有效和完备的。它的推论包括合并规则、伪传递规则和分解规则。
推论规则
-
合并规则 (Union Rule):
- 如果 X→Y 和 X→Z 成立,则 X→YZ 也成立。
- 说明: 可以合并具有相同左部的函数依赖。
-
伪传递规则 (Pseudo Transitivity Rule):
- 如果 X→Y 和 WY→Z 成立,则 XW→Z 也成立。
- 说明: 当函数依赖的右部与另一个函数依赖的左部部分重叠时,可推导出新的函数依赖。
-
分解规则 (Decomposition Rule):
- 如果 X→Y 成立,并且 Z⊆Y,则 X→Z 也成立。
- 说明: 函数依赖的右部可以分解成更小的部分。
重要结论
- 函数依赖 X → A 1 , A 2 , . . . , A n X→A_1,A_2,...,A_n X→A1,A2,...,An 成立的充分必要条件是每个 X → A i X→A_i X→Ai 都成立。
- 函数依赖集 F 的闭包 F + F^+ F+ 是从 F 出发用公理导出的所有函数依赖的集合。
应用
Armstrong 公理系统在数据库设计中被广泛应用于确定关系模式的规范化程度。通过应用这些规则,设计者可以识别数据冗余和更新异常,并据此对数据库模式进行调整,以达到更高级别的规范化。
相关文章:
关系数据理论的函数依赖)
【数据库原理】(16)关系数据理论的函数依赖
一.函数依赖的概念 函数依赖是关系数据库中核心的概念,它指的是在属性集之间存在的一种特定的关系。这种关系表明,一个属性集的值可以唯一确定另一个属性集的值。 属性子集:在关系模式中,X和Y可以是单个属性,也可以是…...

脆弱的SSL加密算法漏洞原理以及修复方法
漏洞名称:弱加密算法、脆弱的加密算法、脆弱的SSL加密算法、openssl的FREAK Attack漏洞 漏洞描述:脆弱的SSL加密算法,是一种常见的漏洞,且至今仍有大量软件支持低强度的加密协议,包括部分版本的openssl。其实…...
)
SVN迁移至GitLab,并附带历史提交记录(二)
与《SVN迁移至GitLab,并附带历史提交记录》用的 git svn clone不同,本文使用svn2git来迁移项目代码。 一、准备工作 安装Git环境,配置本地git账户信息: git config --global user.name "XXX" git config --global us…...
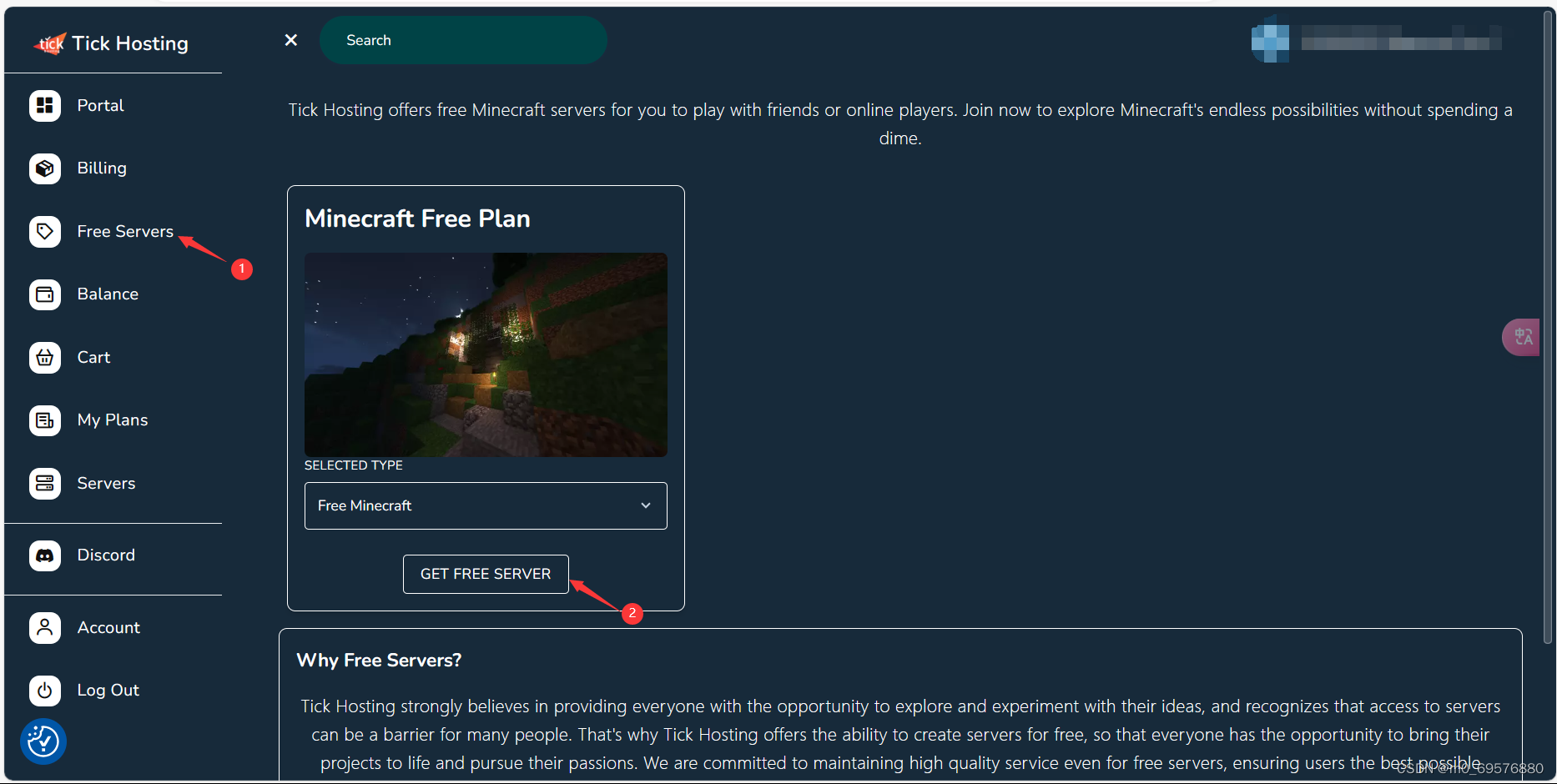
如何创建容器搭建节点
1.注册Discord账号 https://discord.com/这是登录网址: https://discord.com/ 2.点击startnow注册,用discord注册或者邮箱注册都可,然后登录tickhosting Tick Hosting这是登录网址:Tick Hosting 3.创建servers 4.点击你创建的servers,按照图中步骤进行...

微众区块链观察节点的架构和原理 | 科普时间
践行区块链公共精神,实现更好的公众开放与监督!2023年12月,微众区块链观察节点正式面向公众开放接入功能。从开放日起,陆续有多个观察节点在各地运行,同步区块链数据,运行区块链浏览器观察检视数据…...
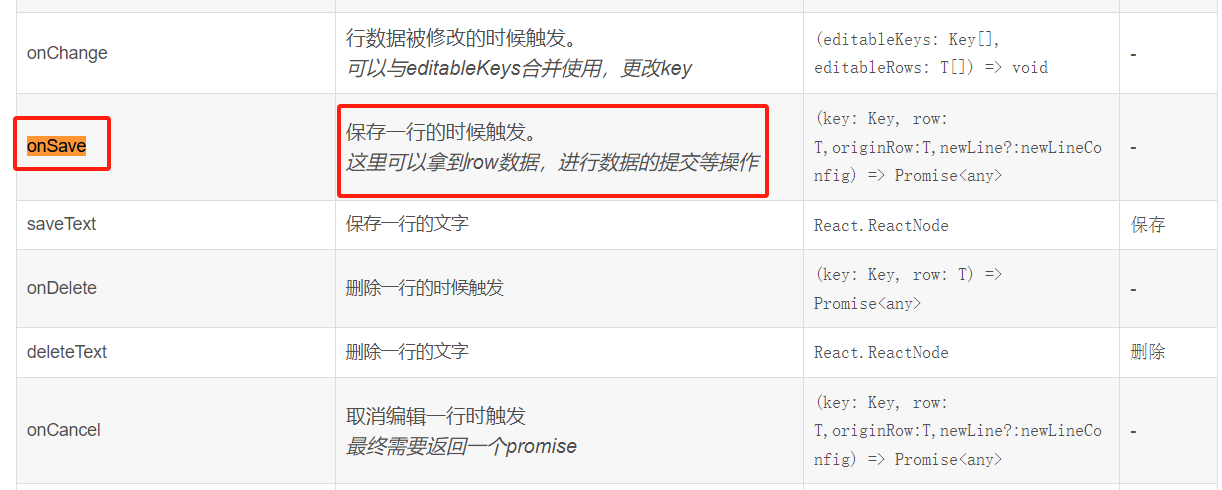
React Admin 前端脚手架之ant-design-pro
文章目录 一、React Admin 前端脚手架选型二、React Admin 前端脚手架之ant-design-pro三、ant-design-pro使用步骤四、调试主题五、常用总结(持续更新)EditableProTable组件 常用组件EditableProTable组件 编辑某行后,保存时候触发发送请求EditableProTable组件,添加记录提…...

向爬虫而生---Redis 基石篇1 <拓展str>
前言: 本来是基于scrapy-redis进行讲解的,需要拓展一下redis; 包含用法,设计,高并发,阻塞等; 要应用到爬虫开发中,这些基础理论我觉得还是有必要了解一下; 所以,新开一栏! 把redis这个环节系统补上,再转回去scrapy-redis才好深入; 正文: Redis是一种内存数据库,…...

【野火i.MX6ULL开发板】利用microUSB线烧入Debian镜像
0、前言 烧入Debian镜像有两种方式:SD卡、USB SD卡:需要SD卡(不是所有型号都可以,建议去了解了解)、SD卡读卡器 USB:需要microUSB线 由于SD卡的网上资料很多了,又因为所需硬件(SD卡…...

“我在大A炒自己”
嘻嘻嘻,大伙儿好像还挺喜欢我闲聊,今天太忙,没得空精进技术,那咱还是接着闲聊吧😂😂 看到标题点进来的各位大A真爱粉,请先收下我的崇高敬意!!别误会,标题说的…...

js 颜色转换,RGB颜色转换为16进制,16进制颜色转为RGB格式
颜色转换,RGB颜色转换为16进制,16进制颜色转为RGB格式,可以自己设置透明度。 //十六进制颜色值的正则表达式 var reg /^#([0-9a-fA-f]{3}|[0-9a-fA-f]{6})$/; /*RGB颜色转换为16进制*/ String.prototype.colorHex function () {var that this;if (/^…...

uniapp中用户登录数据的存储方法探究
Hello大家好!我是咕噜铁蛋!作为一个博主,我们经常需要在应用程序中实现用户登录功能,并且需要将用户的登录数据进行存储,以便在多次使用应用程序时能够方便地获取用户信息。铁蛋通过科技手段帮大家收集整理了些知识&am…...
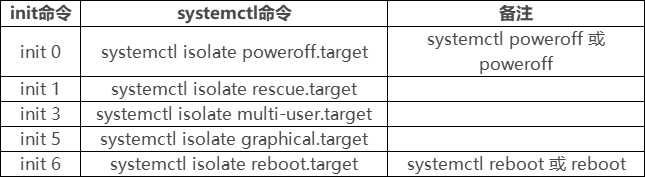
引导过程与服务控制
文章目录 一、Linux操作系统引导过程1、开机启动的完整过程1.1 开机自检(BIOS)1.2 MBR引导1.3 GRUB菜单1.4 加载内核(kernel)1.5 init进程初始化 2、系统初始化进程2.1 init进程2.2 systemdinit与systemd区别 3、Systemd单元类型4…...

《矩阵分析》笔记
来源:【《矩阵分析》期末速成 主讲人:苑长(5小时冲上90)】https://www.bilibili.com/video/BV1A24y1p76q?vd_sourcec4e1c57e5b6ca4824f87e74170ffa64d 这学期考矩阵论,使用教材是《矩阵论简明教程》,因为没…...

『App自动化测试之Appium应用篇』| Appium常用API及操作
『App自动化测试之Appium应用篇』| Appium常用API及操作 1 press_keycode1.1 键盘操作1.2 关于KeyCode1.3 press_keycode源码1.4 电话键相关1.5 控制键相关1.6 基本按键相关1.7 组合键相关1.8 符号键相关1.9 使用举例 2 swip方法2.1 swip说明2.2 swip使用方法2.3 使用示例 3 sc…...
VSCode搭建 .netcore 开发环境
一、MacOS 笔者笔记本电脑上安装的是macOS High Sierra(10.13),想要尝试一下新版本的.netcore,之前系统是10.12时,.netcore 3.1刚出来时安装过3.1版本,很久没更新了,最近.net8出来了,想试一下,…...
python 写自动点击爬取数据
今天来点不一样的!哥们 提示: 这里只是用于自己学习的 ,请勿用违法地方 效果图 会进行点击下一页 进行抓取 需要其他操作也可以自己写 文章目录 今天来点不一样的!哥们前言一、上代码?总结 前言 爬虫是指通过编程自动…...
CSDN博客重新更新
说来惭愧,好久没更新博客文章,导致个人博客网站:https://lenky.info/ 所在的网络空间和域名都过期了都没发觉,直到有个同事在Dim上问我我的个人博客为啥打不开了。。。幸好之前有做整站备份,后续慢慢把内容都迁回CSDN上…...
)
《剑指 Offer》专项突破版 - 面试题 5 : 单词长度的最大乘积(C++ 实现)
目录 前言 方法一 方法二 前言 题目链接:318. 最大单词长度乘积 - 力扣(LeetCode) 题目: 输入一个字符串数组 words,请计算不包含相同字符的两个字符串 words[i] 和 words[j] 的长度乘积的最大值。如果所有字符串…...

【Java集合篇】HashMap的get方法是如何实现的?
HashMap的get方法是如何实现的 ✔️典型解析✔️拓展知识仓✔️如何避免HashMap get方法的哈希重✔️HashMap get方法的优缺点有哪些✔️HashMap get方法的是线程安全的吗✔️什么是ConcurrentHashMap✔️ConcurrentHashMap有哪些应用场景✔️ConcurrentHashMap的优缺点 ✔️源…...
Java学习苦旅(二十二)——MapSet
本篇博客将详细讲解Map和Set。 文章目录 搜索概念模型 MapMap.Entry<K, V>Map的常用方法说明TreeMap和HashMap的区别 Set常用方法说明TreeSet和HashSet的区别 结尾 搜索 概念 Map和set是一种专门用来进行搜索的容器或者数据结构,其搜索的效率与其具体的实例…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...

密码学基础——SM4算法
博客主页:christine-rr-CSDN博客 专栏主页:密码学 📌 【今日更新】📌 对称密码算法——SM4 目录 一、国密SM系列算法概述 二、SM4算法 2.1算法背景 2.2算法特点 2.3 基本部件 2.3.1 S盒 2.3.2 非线性变换 编辑…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...

海云安高敏捷信创白盒SCAP入选《中国网络安全细分领域产品名录》
近日,嘶吼安全产业研究院发布《中国网络安全细分领域产品名录》,海云安高敏捷信创白盒(SCAP)成功入选软件供应链安全领域产品名录。 在数字化转型加速的今天,网络安全已成为企业生存与发展的核心基石,为了解…...

UE5 音效系统
一.音效管理 音乐一般都是WAV,创建一个背景音乐类SoudClass,一个音效类SoundClass。所有的音乐都分为这两个类。再创建一个总音乐类,将上述两个作为它的子类。 接着我们创建一个音乐混合类SoundMix,将上述三个类翻入其中,通过它管理每个音乐…...
