视觉SLAM十四讲|【四】误差Jacobian推导
视觉SLAM十四讲|【四】误差Jacobian推导
预积分误差递推公式
ω = 1 2 ( ( ω b k + n k g − b k g ) + ( w b k + 1 + n k + 1 g − b k + 1 g ) ) \omega = \frac{1}{2}((\omega_b^k+n_k^g-b_k^g)+(w_b^{k+1}+n_{k+1}^g-b_{k+1}^g)) ω=21((ωbk+nkg−bkg)+(wbk+1+nk+1g−bk+1g))
其中, w b k w_b^k wbk为 k k k时刻下body坐标系的角速度, n k g n_k^g nkg为 k k k时刻下陀螺仪白噪声, b k g b_k^g bkg为 k k k时刻下陀螺仪偏置量。 n k a n_k^a nka为 k k k时刻下加速度白噪声, b k a b_k^a bka为 k k k时刻下加速度偏置量。 k + 1 k+1 k+1时刻下记号同理。
q b i b k + 1 = q b i b k ⊗ [ 1 , 1 2 ω δ t ] T q_{b_i b_{k+1}} = q_{b_i b_k} \otimes [1, \frac{1}{2} \omega \delta t]^T qbibk+1=qbibk⊗[1,21ωδt]T
a = 1 2 ( q b i b k ( a b k + n b k − b k a ) + q b i b k + 1 ( a b k + 1 + n b k + 1 − b k + 1 a ) ) a = \frac{1}{2}(q_{b_i b_{k}} (a_b^k + n_b^k -b_k^a) + q_{b_i b_{k+1}} (a_b^{k+1} + n_b^{k+1} - b_{k+1}^a)) a=21(qbibk(abk+nbk−bka)+qbibk+1(abk+1+nbk+1−bk+1a))
α b i b k + 1 = α b i b k + β b i b k δ t + 1 2 a δ t 2 \alpha_{b_i b_{k+1}} = \alpha_{b_i b_{k}} + \beta_{b_i b_k} \delta t + \frac{1}{2}a \delta t^2 αbibk+1=αbibk+βbibkδt+21aδt2
β b i b k + 1 = β b i b k + a δ t \beta_{b_i b_{k+1}} = \beta_{b_i b_{k}} + a\delta t βbibk+1=βbibk+aδt
b k + 1 a = b k a + n b k a δ t b_{k+1}^a = b_k^a + n_{b_k^a}\delta t bk+1a=bka+nbkaδt
b k + 1 g = b k g + n b k g δ t b_{k+1}^g = b_k^g + n_{b_k^g}\delta t bk+1g=bkg+nbkgδt
示例1
f 15 = δ α b i b k + 1 δ b k g f_{15} = \frac{\delta \alpha_{b_i b_{k+1}}}{\delta b_k^g} f15=δbkgδαbibk+1
由上面的递推公式可知
α b i b k + 1 = α b i b k + β b i b k δ t + 1 2 a δ t 2 \alpha_{b_i b_{k+1}} = \alpha_{b_i b_{k}} + \beta_{b_i b_k} \delta t + \frac{1}{2}a \delta t^2 αbibk+1=αbibk+βbibkδt+21aδt2
其中, α b i b k \alpha_{b_i b_{k}} αbibk、 β b i b k δ t \beta_{b_i b_k}\delta t βbibkδt都与 b k g b_k^g bkg无关,可以省略,而很容易看出 a a a中含有 q b i b k + 1 q_{b_i b_{k+1}} qbibk+1项,其中进一步含有对 b k g b_k^g bkg相关的元素,必须保留。因此进一步推得
f 15 = δ 1 2 a δ t 2 δ b k g f_{15} = \frac{\delta \frac{1}{2} a \delta t^2}{\delta b_k^g} f15=δbkgδ21aδt2
其中,
a = 1 2 ( q b i b k ( a b k + n b k − b k a ) + q b i b k + 1 ( a b k + 1 + n b k + 1 − b k + 1 a ) ) a = \frac{1}{2}(q_{b_i b_{k}} (a_b^k + n_b^k -b_k^a) + q_{b_i b_{k+1}} (a_b^{k+1} + n_b^{k+1} - b_{k+1}^a)) a=21(qbibk(abk+nbk−bka)+qbibk+1(abk+1+nbk+1−bk+1a))
q b i b k ( a b k + n b k − b k a ) q_{b_i b_{k}} (a_b^k + n_b^k -b_k^a) qbibk(abk+nbk−bka)依然与 b k g b_k^g bkg无关,可以省略。
f 15 = δ 1 4 q b i b k + 1 ( a b k + 1 + n b k + 1 − b k + 1 a ) δ t 2 δ b k g f_{15}=\frac{\delta \frac{1}{4} q_{b_i b_{k+1}} (a_b^{k+1} + n_b^{k+1} - b_{k+1}^a) \delta t^2}{\delta b_k^g} f15=δbkgδ41qbibk+1(abk+1+nbk+1−bk+1a)δt2
白噪声项不可知,拿掉
f 15 = δ 1 4 q b i b k + 1 ( a b k + 1 − b k + 1 a ) δ t 2 δ b k g f_{15}=\frac{\delta \frac{1}{4} q_{b_i b_{k+1}} (a_b^{k+1} - b_{k+1}^a) \delta t^2}{\delta b_k^g} f15=δbkgδ41qbibk+1(abk+1−bk+1a)δt2
f 15 = δ 1 4 q b i b k + 1 ( a b k + 1 − b k + 1 a ) δ t 2 δ b k g f_{15}=\frac{\delta \frac{1}{4} q_{b_i b_{k+1}} (a_b^{k+1} - b_{k+1}^a) \delta t^2}{\delta b_k^g} f15=δbkgδ41qbibk+1(abk+1−bk+1a)δt2
q b i b k + 1 = q b i b k ⊗ [ 1 , 1 2 ω δ t ] T q_{b_i b_{k+1}} = q_{b_i b_k} \otimes [1, \frac{1}{2} \omega \delta t]^T qbibk+1=qbibk⊗[1,21ωδt]T
f 15 = δ 1 4 q b i b k ⊗ [ 1 , 1 2 ω δ t ] T ( a b k + 1 − b k + 1 a ) δ t 2 δ b k g f_{15}=\frac{\delta \frac{1}{4} q_{b_i b_k} \otimes [1, \frac{1}{2} \omega \delta t]^T (a_b^{k+1} - b_{k+1}^a) \delta t^2}{\delta b_k^g} f15=δbkgδ41qbibk⊗[1,21ωδt]T(abk+1−bk+1a)δt2
其中
ω = 1 2 ( ( ω b k + n k g − b k g ) + ( w b k + 1 + n k + 1 g − b k + 1 g ) ) \omega = \frac{1}{2}((\omega_b^k+n_k^g-b_k^g)+(w_b^{k+1}+n_{k+1}^g-b_{k+1}^g)) ω=21((ωbk+nkg−bkg)+(wbk+1+nk+1g−bk+1g))
去除不可知的白噪声项
ω = 1 2 ( ( ω b k − b k g ) + ( w b k + 1 − b k + 1 g ) ) \omega = \frac{1}{2}((\omega_b^k-b_k^g)+(w_b^{k+1}-b_{k+1}^g)) ω=21((ωbk−bkg)+(wbk+1−bk+1g))
由于 k + 1 k+1 k+1时刻的信息并不知道,在此处如果不使用中值积分,直接使用初始值,有
ω = ω b k − b k g \omega =\omega_b^k-b_k^g ω=ωbk−bkg
f 15 = δ 1 4 q b i b k ⊗ [ 1 , 1 2 ( ω b k − b k g ) δ t ] T ( a b k + 1 − b k + 1 a ) δ t 2 δ b k g f_{15}=\frac{\delta \frac{1}{4} q_{b_i b_k} \otimes [1, \frac{1}{2} (\omega_b^k-b_k^g) \delta t]^T (a_b^{k+1} - b_{k+1}^a) \delta t^2}{\delta b_k^g} f15=δbkgδ41qbibk⊗[1,21(ωbk−bkg)δt]T(abk+1−bk+1a)δt2
此时,为了便于计算,我们需要把四元数表示旋转转换为用旋转矩阵表示矩阵的旋转,得到
f 15 = 1 4 δ R b i b k exp ( ( ( w b k − b k g ) δ t ) ∧ ) ( a b k + 1 − b k + 1 a ) δ t 2 δ b k g f_{15}=\frac{1}{4} \frac{\delta R_{b_i b_k} \exp(((w_b^k-b_k^g)\delta t)^{\wedge})(a_b^{k+1} - b_{k+1}^a)\delta t^2}{\delta b_k^g} f15=41δbkgδRbibkexp(((wbk−bkg)δt)∧)(abk+1−bk+1a)δt2
观察式子,我们要想办法把 b k g b_k^g bkg拆出来。回顾上一章,李代数旋转有性质
l n ( R e x p ( ϕ ∧ ) ) ∨ = l n ( R ) ∨ + J r − 1 ϕ ln(Rexp(\phi^{\land}))^{\vee}=ln(R)^{\vee}+J_r^{-1}\phi ln(Rexp(ϕ∧))∨=ln(R)∨+Jr−1ϕ
类似的,对于非对数情况,有
exp ( ( ϕ + δ ϕ ) ∧ ) = exp ( ϕ ∧ ) exp ( ( J r ( ϕ ) δ ϕ ) ∧ ) \exp( (\phi + \delta\phi)^{\wedge} )= \exp(\phi^{\wedge})\exp((J_r(\phi)\delta\phi)^{\wedge}) exp((ϕ+δϕ)∧)=exp(ϕ∧)exp((Jr(ϕ)δϕ)∧)
lim ϕ → 0 J r ( ϕ ) = I \lim_{\phi \rightarrow 0} J_r(\phi)=I ϕ→0limJr(ϕ)=I
exp ( ( ( w b k − b k g ) δ t ) ∧ = exp ( ( w b k δ t ) ∧ ) exp ( ( J r ( w b k δ t ) ( − b k g δ t ) ) ∧ ) \exp(((w_b^k-b_k^g)\delta t)^{\wedge}=\exp((w_b^k\delta t)^{\wedge})\exp((J_r(w_b^k\delta t)(-b_k^g \delta t))^{\wedge}) exp(((wbk−bkg)δt)∧=exp((wbkδt)∧)exp((Jr(wbkδt)(−bkgδt))∧)
f 15 = 1 4 δ R b i b k exp ( ( ( w b k − b k g ) δ t ) ∧ ) ( a b k + 1 − b k + 1 a ) δ t 2 δ b k g f_{15}=\frac{1}{4} \frac{\delta R_{b_i b_k} \exp(((w_b^k-b_k^g)\delta t)^{\wedge})(a_b^{k+1} - b_{k+1}^a)\delta t^2}{\delta b_k^g} f15=41δbkgδRbibkexp(((wbk−bkg)δt)∧)(abk+1−bk+1a)δt2
f 15 = 1 4 δ R b i b k exp ( ( w b k δ t ) ∧ ) exp ( ( J r ( w b k δ t ) ( − b k g δ t ) ) ∧ ) ( a b k + 1 − b k + 1 a ) δ t 2 δ b k g f_{15}=\frac{1}{4} \frac{\delta R_{b_i b_k} \exp((w_b^k\delta t)^{\wedge})\exp((J_r(w_b^k\delta t)(-b_k^g \delta t))^{\wedge})(a_b^{k+1} - b_{k+1}^a)\delta t^2}{\delta b_k^g} f15=41δbkgδRbibkexp((wbkδt)∧)exp((Jr(wbkδt)(−bkgδt))∧)(abk+1−bk+1a)δt2
w b k δ t → 0 w_b^k\delta t \rightarrow0 wbkδt→0
f 15 = 1 4 δ R b i b k exp ( ( J r ( w b k δ t ) ( − b k g δ t ) ) ∧ ) ( a b k + 1 − b k + 1 a ) δ t 2 δ b k g f_{15}=\frac{1}{4} \frac{\delta R_{b_i b_k} \exp((J_r(w_b^k\delta t)(-b_k^g \delta t))^{\wedge})(a_b^{k+1} - b_{k+1}^a)\delta t^2}{\delta b_k^g} f15=41δbkgδRbibkexp((Jr(wbkδt)(−bkgδt))∧)(abk+1−bk+1a)δt2
f 15 = 1 4 δ R b i b k exp ( ( − b k g δ t ) ) ∧ ) ( a b k + 1 − b k + 1 a ) δ t 2 δ b k g f_{15}=\frac{1}{4} \frac{\delta R_{b_i b_k} \exp((-b_k^g \delta t))^{\wedge})(a_b^{k+1} - b_{k+1}^a)\delta t^2}{\delta b_k^g} f15=41δbkgδRbibkexp((−bkgδt))∧)(abk+1−bk+1a)δt2
f 15 = 1 4 δ R b i b k ( I + ( − b k g δ t ) ) ∧ ) ( a b k + 1 − b k + 1 a ) δ t 2 δ b k g f_{15}=\frac{1}{4} \frac{\delta R_{b_i b_k} (I+(-b_k^g \delta t))^{\wedge})(a_b^{k+1} - b_{k+1}^a)\delta t^2}{\delta b_k^g} f15=41δbkgδRbibk(I+(−bkgδt))∧)(abk+1−bk+1a)δt2
f 15 = 1 4 δ R b i b k ( − b k g δ t ) ∧ ( a b k + 1 − b k + 1 a ) δ t 2 δ b k g f_{15}=\frac{1}{4} \frac{\delta R_{b_i b_k} (-b_k^g \delta t)^{\wedge}(a_b^{k+1} - b_{k+1}^a)\delta t^2}{\delta b_k^g} f15=41δbkgδRbibk(−bkgδt)∧(abk+1−bk+1a)δt2
使用伴随性质,有
f 15 = 1 4 δ R b i b k ( a b k + 1 − b k + 1 a ) ∧ ( b k g δ t ) δ t 2 δ b k g f_{15}=\frac{1}{4} \frac{\delta R_{b_i b_k} (a_b^{k+1} - b_{k+1}^a)^{\wedge}(b_k^g \delta t)\delta t^2}{\delta b_k^g} f15=41δbkgδRbibk(abk+1−bk+1a)∧(bkgδt)δt2
f 15 = 1 4 R b i b k ( a b k + 1 − b k + 1 a ) ∧ δ t 2 δ t f_{15}=\frac{1}{4} R_{b_i b_k} (a_b^{k+1} - b_{k+1}^a)^{\wedge} \delta t^2 \delta t f15=41Rbibk(abk+1−bk+1a)∧δt2δt
示例2
g 12 = δ α b i b k + 1 δ n k g g_{12}=\frac{\delta \alpha_{b_i b_{k+1}}}{\delta n_k^g} g12=δnkgδαbibk+1
一看 n k g n_k^g nkg就知道又要找和旋转有关的量了。回顾递推公式,有
ω = 1 2 ( ( ω b k + n k g − b k g ) + ( w b k + 1 + n k + 1 g − b k + 1 g ) ) \omega = \frac{1}{2}((\omega_b^k+n_k^g-b_k^g)+(w_b^{k+1}+n_{k+1}^g-b_{k+1}^g)) ω=21((ωbk+nkg−bkg)+(wbk+1+nk+1g−bk+1g))
q b i b k + 1 = q b i b k ⊗ [ 1 , 1 2 ω δ t ] T q_{b_i b_{k+1}} = q_{b_i b_k} \otimes [1, \frac{1}{2} \omega \delta t]^T qbibk+1=qbibk⊗[1,21ωδt]T
a = 1 2 ( q b i b k ( a b k + n b k − b k a ) + q b i b k + 1 ( a b k + 1 + n b k + 1 − b k + 1 a ) ) a = \frac{1}{2}(q_{b_i b_{k}} (a_b^k + n_b^k -b_k^a) + q_{b_i b_{k+1}} (a_b^{k+1} + n_b^{k+1} - b_{k+1}^a)) a=21(qbibk(abk+nbk−bka)+qbibk+1(abk+1+nbk+1−bk+1a))
α b i b k + 1 = α b i b k + β b i b k δ t + 1 2 a δ t 2 \alpha_{b_i b_{k+1}} = \alpha_{b_i b_{k}} + \beta_{b_i b_k} \delta t + \frac{1}{2}a \delta t^2 αbibk+1=αbibk+βbibkδt+21aδt2
有
g 12 = δ α b i b k + 1 δ n k g g_{12}=\frac{\delta \alpha_{b_i b_{k+1}}}{\delta n_k^g} g12=δnkgδαbibk+1
g 12 = δ 1 2 a δ t 2 δ n k g g_{12}=\frac{\delta \frac{1}{2}a \delta t^2}{\delta n_k^g} g12=δnkgδ21aδt2
a = 1 2 ( q b i b k ( a b k + n b k − b k a ) + q b i b k + 1 ( a b k + 1 + n b k + 1 − b k + 1 a ) ) a = \frac{1}{2}(q_{b_i b_{k}} (a_b^k + n_b^k -b_k^a) + q_{b_i b_{k+1}} (a_b^{k+1} + n_b^{k+1} - b_{k+1}^a)) a=21(qbibk(abk+nbk−bka)+qbibk+1(abk+1+nbk+1−bk+1a))
g 12 = δ 1 4 q b i b k + 1 ( a b k + 1 − b k + 1 a ) δ t 2 δ n k g g_{12}=\frac{\delta \frac{1}{4}q_{b_i b_{k+1}} (a_b^{k+1} - b_{k+1}^a) \delta t^2}{\delta n_k^g} g12=δnkgδ41qbibk+1(abk+1−bk+1a)δt2
又因为
q b i b k + 1 = q b i b k ⊗ [ 1 , 1 2 ω δ t ] T q_{b_i b_{k+1}} = q_{b_i b_k} \otimes [1, \frac{1}{2} \omega \delta t]^T qbibk+1=qbibk⊗[1,21ωδt]T
所以有
g 12 = δ 1 4 q b i b k ⊗ [ 1 , 1 2 ω δ t ] T ( a b k + 1 − b k + 1 a ) δ t 2 δ n k g g_{12}=\frac{\delta \frac{1}{4}q_{b_i b_k} \otimes [1, \frac{1}{2} \omega \delta t]^T (a_b^{k+1} - b_{k+1}^a) \delta t^2}{\delta n_k^g} g12=δnkgδ41qbibk⊗[1,21ωδt]T(abk+1−bk+1a)δt2
ω = 1 2 ( ( ω b k + n k g − b k g ) + ( w b k + 1 + n k + 1 g − b k + 1 g ) ) \omega = \frac{1}{2}((\omega_b^k+n_k^g-b_k^g)+(w_b^{k+1}+n_{k+1}^g-b_{k+1}^g)) ω=21((ωbk+nkg−bkg)+(wbk+1+nk+1g−bk+1g))
g 12 = δ 1 4 q b i b k ⊗ [ 1 , 1 2 ( ω b k + 1 2 n k g ) δ t ] T ( a b k + 1 − b k + 1 a ) δ t 2 δ n k g g_{12}=\frac{\delta \frac{1}{4}q_{b_i b_k} \otimes [1, \frac{1}{2} (\omega_b^k+\frac{1}{2}n_k^g)\delta t]^T (a_b^{k+1} - b_{k+1}^a) \delta t^2}{\delta n_k^g} g12=δnkgδ41qbibk⊗[1,21(ωbk+21nkg)δt]T(abk+1−bk+1a)δt2
g 12 = 1 4 δ R b i b k exp ( ( ( ω b k + 1 2 n k g ) δ t ) ∧ ) ( a b k + 1 − b k + 1 a ) δ t 2 δ n k g g_{12}=\frac{1}{4} \frac{\delta R_{b_i b_k} \exp(((\omega_b^k+\frac{1}{2}n_k^g)\delta t)^{\wedge})(a_b^{k+1} - b_{k+1}^a) \delta t^2}{\delta n_k^g} g12=41δnkgδRbibkexp(((ωbk+21nkg)δt)∧)(abk+1−bk+1a)δt2
g 12 = 1 4 δ R b i b k ( exp ( ( ω b k δ t ) ∧ ) ) ( exp ( ( J r ( ω b k δ t ) 1 2 n k g δ t ) ∧ ) ) ( a b k + 1 − b k + 1 a ) δ t 2 δ n k g g_{12}=\frac{1}{4} \frac{\delta R_{b_i b_k} (\exp((\omega_b^k\delta t)^{\wedge}))(\exp((J_r(\omega_b^k\delta t)\frac{1}{2}n_k^g \delta t)^{\wedge}))(a_b^{k+1} - b_{k+1}^a) \delta t^2}{\delta n_k^g} g12=41δnkgδRbibk(exp((ωbkδt)∧))(exp((Jr(ωbkδt)21nkgδt)∧))(abk+1−bk+1a)δt2
g 12 = 1 4 δ R b i b k ( exp ( ( J r ( ω b k δ t ) 1 2 n k g δ t ) ∧ ) ) ( a b k + 1 − b k + 1 a ) δ t 2 δ n k g g_{12}=\frac{1}{4} \frac{\delta R_{b_i b_k}(\exp((J_r(\omega_b^k\delta t)\frac{1}{2}n_k^g \delta t)^{\wedge}))(a_b^{k+1} - b_{k+1}^a) \delta t^2}{\delta n_k^g} g12=41δnkgδRbibk(exp((Jr(ωbkδt)21nkgδt)∧))(abk+1−bk+1a)δt2
g 12 = 1 4 δ R b i b k ( exp ( ( 1 2 n k g δ t ) ∧ ) ) ( a b k + 1 − b k + 1 a ) δ t 2 δ n k g g_{12}=\frac{1}{4} \frac{\delta R_{b_i b_k}(\exp((\frac{1}{2}n_k^g \delta t)^{\wedge}))(a_b^{k+1} - b_{k+1}^a) \delta t^2}{\delta n_k^g} g12=41δnkgδRbibk(exp((21nkgδt)∧))(abk+1−bk+1a)δt2
g 12 = 1 4 δ R b i b k ( ( 1 2 n k g δ t ) ∧ ) ( a b k + 1 − b k + 1 a ) δ t 2 δ n k g g_{12}=\frac{1}{4} \frac{\delta R_{b_i b_k}((\frac{1}{2}n_k^g \delta t)^{\wedge})(a_b^{k+1} - b_{k+1}^a) \delta t^2}{\delta n_k^g} g12=41δnkgδRbibk((21nkgδt)∧)(abk+1−bk+1a)δt2
g 12 = − 1 4 δ R b i b k ( a b k + 1 − b k + 1 a ) ∧ ( 1 2 n k g δ t ) δ t 2 δ n k g g_{12}=-\frac{1}{4} \frac{\delta R_{b_i b_k}(a_b^{k+1} - b_{k+1}^a)^{\wedge} (\frac{1}{2}n_k^g \delta t)\delta t^2}{\delta n_k^g} g12=−41δnkgδRbibk(abk+1−bk+1a)∧(21nkgδt)δt2
g 12 = − 1 4 R b i b k ( a b k + 1 − b k + 1 a ) ∧ ( 1 2 δ t ) δ t 2 g_{12}=-\frac{1}{4} R_{b_i b_k}(a_b^{k+1} - b_{k+1}^a)^{\wedge} (\frac{1}{2} \delta t)\delta t^2 g12=−41Rbibk(abk+1−bk+1a)∧(21δt)δt2
g 12 = − 1 8 R b i b k ( a b k + 1 − b k + 1 a ) ∧ ( δ t ) δ t 2 g_{12}=-\frac{1}{8} R_{b_i b_k}(a_b^{k+1} - b_{k+1}^a)^{\wedge} (\delta t)\delta t^2 g12=−81Rbibk(abk+1−bk+1a)∧(δt)δt2
Levenberg-Marquardt方法证明
Levenberg (1944) 和 Marquardt (1963) 先后对高斯牛顿法进行了改进,求解过程中引入了阻尼因子
( J T J + μ I ) Δ x l m = − J T f , μ > 0 (J^TJ+\mu I) \Delta x_{lm} = -J^Tf,\mu >0 (JTJ+μI)Δxlm=−JTf,μ>0
J = δ F δ x J = \frac{\delta F}{\delta x} J=δxδF
相关文章:

视觉SLAM十四讲|【四】误差Jacobian推导
视觉SLAM十四讲|【四】误差Jacobian推导 预积分误差递推公式 ω 1 2 ( ( ω b k n k g − b k g ) ( w b k 1 n k 1 g − b k 1 g ) ) \omega \frac{1}{2}((\omega_b^kn_k^g-b_k^g)(w_b^{k1}n_{k1}^g-b_{k1}^g)) ω21((ωbknkg−bkg)(wbk1nk1g−bk1g)) …...
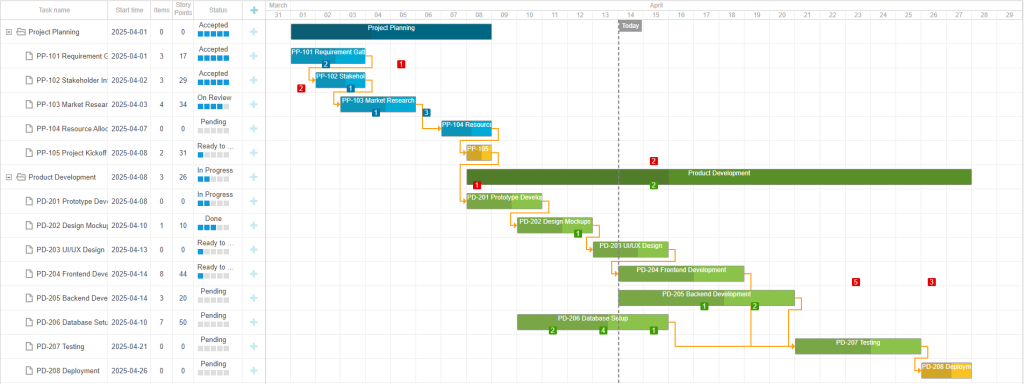
「实战应用」如何用DHTMLX Gantt构建类似JIRA式的项目路线图(一)
DHTMLX Gantt是用于跨浏览器和跨平台应用程序的功能齐全的Gantt图表。可满足项目管理应用程序的所有需求,是最完善的甘特图图表库。 在web项目中使用DHTMLX Gantt时,开发人员经常需要满足与UI外观相关的各种需求。因此他们必须确定JavaScript甘特图库的…...

【习题】应用程序框架
判断题 1. 一个应用只能有一个UIAbility。错误(False) 正确(True)错误(False) 2. 创建的Empty Ability模板工程,初始会生成一个UIAbility文件。正确(True) 正确(True)错误(False) 3. 每调用一次router.pushUrl()方法,页面路由栈数量均会加1。错误(Fal…...
java基于ssm的线上选课系统的设计与实现论文
摘 要 在如今社会上,关于信息上面的处理,没有任何一个企业或者个人会忽视,如何让信息急速传递,并且归档储存查询,采用之前的纸张记录模式已经不符合当前使用要求了。所以,对学生选课信息管理的提升&#x…...
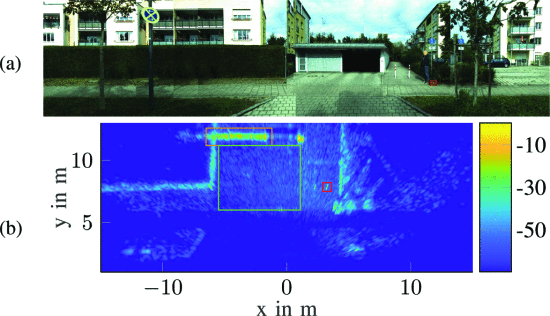
汽车雷达:实时SAR成像的实现
摘要: 众所周知,点云成像是目前实现汽车雷达感知最流行的方案,尤其是采用多级联实现的4D点云成像雷达,这是目前最有希望实现产品落地的技术方案之一。 今天重点分享关于汽车雷达SAR成像相关技术内容,这也证实了4D点云成像雷达并不一定就是汽车雷达成像唯一的方案,在业内…...
《C++语言程序设计(第5版)》(清华大学出版社,郑莉 董渊编著)习题——第2章 C++语言简单程序设计
2-15 编写一个程序,运行时提示输入一个数字,再把这个数字显示出来。 #include <iostream>using namespace std;int main() {// 提示用户输入数字cout << "请输入一个数字: ";// 用于存储用户输入的数字的变量double number;// 从…...

2023年生成式AI全球使用报告
生成式人工智能工具正在迅速改变多个领域,从营销和新闻到教育和艺术。 这些工具使用算法从大量培训材料中获取新的文本、音频或图像。虽然 ChatGPT 和 Midjourney 之类的工具可以用来实现超出人类能力或想象力的艺术效果,但目前它们最常用于比人类更轻松…...

安全防御之漏洞扫描技术
每年都有数以千计的网络安全漏洞被发现和公布,加上攻击者手段的不断变化,网络安全状况也在随着安全漏洞的增加变得日益严峻。寻根溯源,绝大多数用户缺乏一套完整、有效的漏洞管理工作流程,未能落实定期评估与漏洞修补工作。只有比…...
SPON世邦 IP网络对讲广播系统 多处文件上传漏洞复现
0x01 产品简介 SPON世邦IP网络对讲广播系统是一种先进的通信解决方案,旨在提供高效的网络对讲和广播功能。 0x02 漏洞概述 SPON世邦IP网络对讲广播系统 addscenedata.php、uploadjson.php、my_parser.php等接口处存在任意文件上传漏洞,未经身份验证的攻击者可利用此漏洞上…...
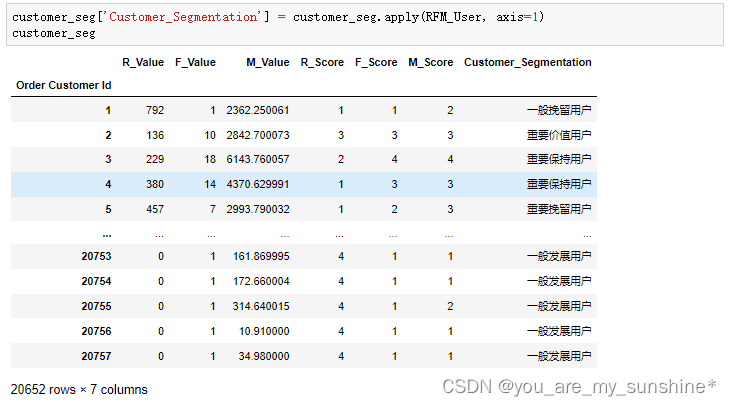
Python综合数据分析_RFM用户分层模型
文章目录 1.数据加载2.查看数据情况3.数据合并及填充4.查看特征字段之间相关性5.聚合操作6.时间维度上看销售额7.计算用户RFM8.数据保存存储(1).to_csv(1).to_pickle 1.数据加载 import pandas as pd dataset pd.read_csv(SupplyChain.csv, encodingunicode_escape) dataset2…...
【C++进阶04】STL中map、set、multimap、multiset的介绍及使用
一、关联式容器 vector/list/deque… 这些容器统称为序列式容器 因为其底层为线性序列的数据结构 里面存储的是元素本身 map/set… 这些容器统称为关联式容器 关联式容器也是用来存储数据的 与序列式容器不同的是 其里面存储的是<key, value>结构的键值对 在数据检索时…...

在 Linux 中开启 Flask 项目持续运行
在 Linux 中开启 Flask 项目持续运行 在部署 Flask 项目时,情况往往并不是那么理想。默认情况下,关闭 SSH 终端后,Flask 服务就停止了。这时,您需要找到一种方法在 Linux 服务器上实现持续运行 Flask 项目,并在服务器…...

考研个人经验总结【心理向】
客官你好 首先,不管你是以何种原因来到这篇博客,以下内容或多或少可能带给你一些启发。如果你还是大二or大三学生,有考研的打算,不妨提前了解一些考研必备的心理战术,有时候并不是你知识学得不好,而是思维…...
如何在CentOS安装SQL Server数据库并通过内网穿透工具实现公网访问
文章目录 前言1. 安装sql server2. 局域网测试连接3. 安装cpolar内网穿透4. 将sqlserver映射到公网5. 公网远程连接6.固定连接公网地址7.使用固定公网地址连接 前言 简单几步实现在Linux centos环境下安装部署sql server数据库,并结合cpolar内网穿透工具࿰…...

jupyter内核错误
1、在dos窗口输入以下命令激活环境:anaconda activate 【py环境名,比如py37】(目的是新家你一个虚拟环境) 2、在虚拟环境py37下安装jupyter notebook,命令:pip install jupyter notebook 3、安装ipykerne…...
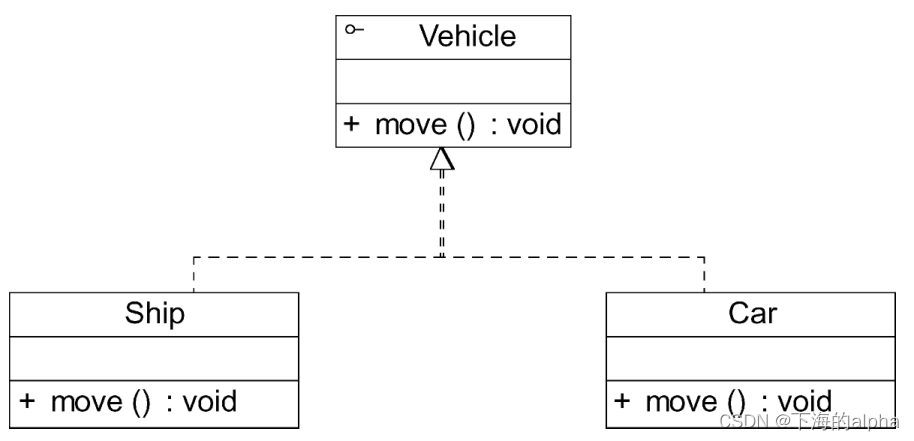
设计模式的艺术P1基础—2.3 类之间的关系
设计模式的艺术P1基础—2.3 类之间的关系 在软件系统中,类并不是孤立存在的,类与类之间存在各种关系。对于不同类型的关系,UML提供了不同的表示方式 1.关联关系 关联(Association)关系是类与类之间最常用…...

工业无人机行业研究:预计2025年将达到108.2亿美元
近年来,在技术进步和各行各业对无人驾驶飞行器 (UAV) 不断增长的需求的推动下,工业无人机市场一直在快速增长。该市场有望在未来几年继续其增长轨迹,许多关键趋势和因素推动其发展。 在全球范围内,工业无人机市场预计到 2025 年将…...

PCA主成分分析算法
在数据分析中,如果特征太多,或者特征之间的相关性太高,通常可以用PCA来进行降维。比如通过对原有10个特征的线性组合, 我们找出3个主成分,就足以解释绝大多数的方差,该算法在高维数据集中被广泛应用。 算法(…...
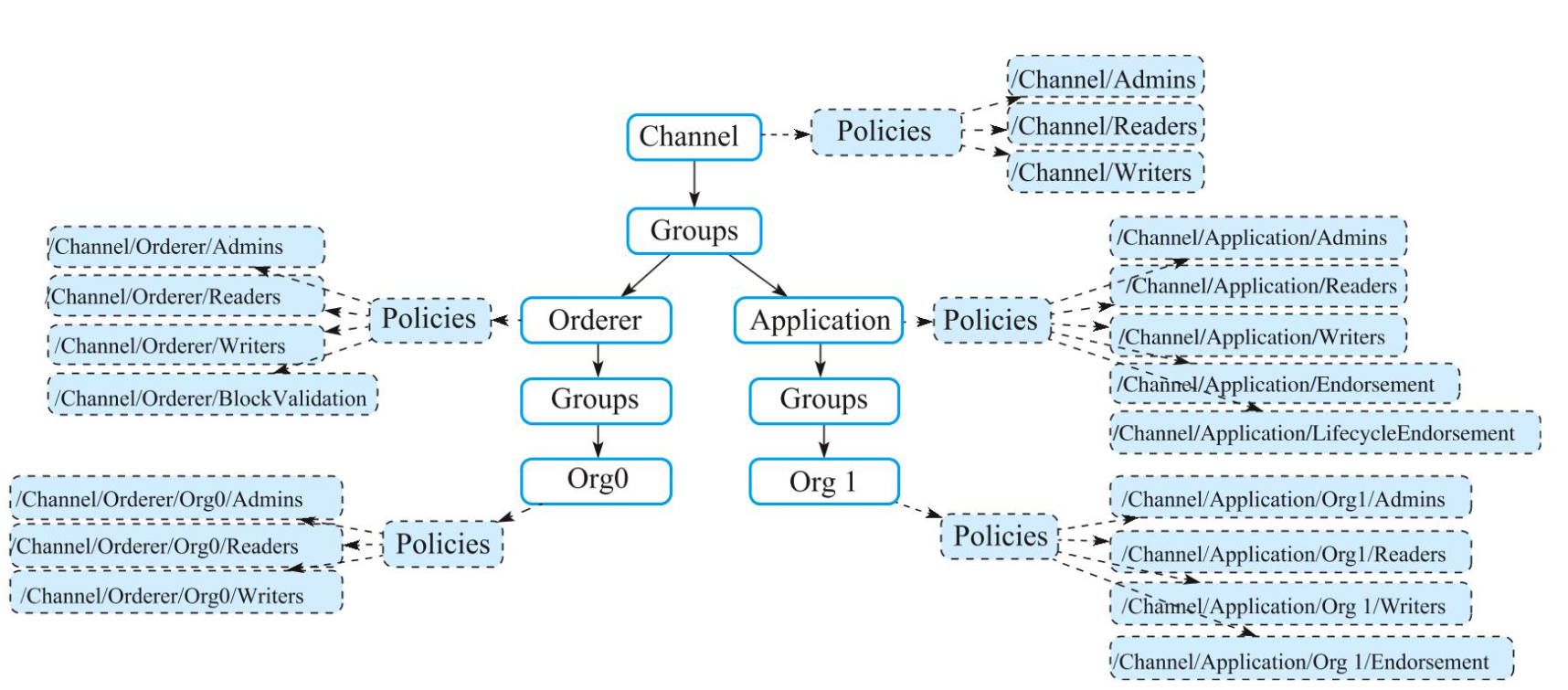
Hyperledger Fabric 权限策略和访问控制
访问控制是区块链网络十分重要的功能,负责控制某个身份在某个场景下是否允许采取某个操作(如读写某个资源)。 常见的访问控制模型包括强制访问控制(Mandatory Access Control)、自主访问控制(Discretionar…...

Day28 回溯算法part04 93. 复原IP地址 78. 子集 90. 子集 II
回溯算法part04 93. 复原IP地址 78. 子集 90. 子集 II 93. 复原 IP 地址 class Solution { private:vector<string> result;bool isValid(string& s,int start,int end){if (start > end) return false;if (s[start] 0 && start ! end) { // 0开头的数…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...

【Ftrace 专栏】Ftrace 参考博文
ftrace、perf、bcc、bpftrace、ply、simple_perf的使用Ftrace 基本用法Linux 利用 ftrace 分析内核调用如何利用ftrace精确跟踪特定进程调度信息使用 ftrace 进行追踪延迟Linux-培训笔记-ftracehttps://www.kernel.org/doc/html/v4.18/trace/events.htmlhttps://blog.csdn.net/…...
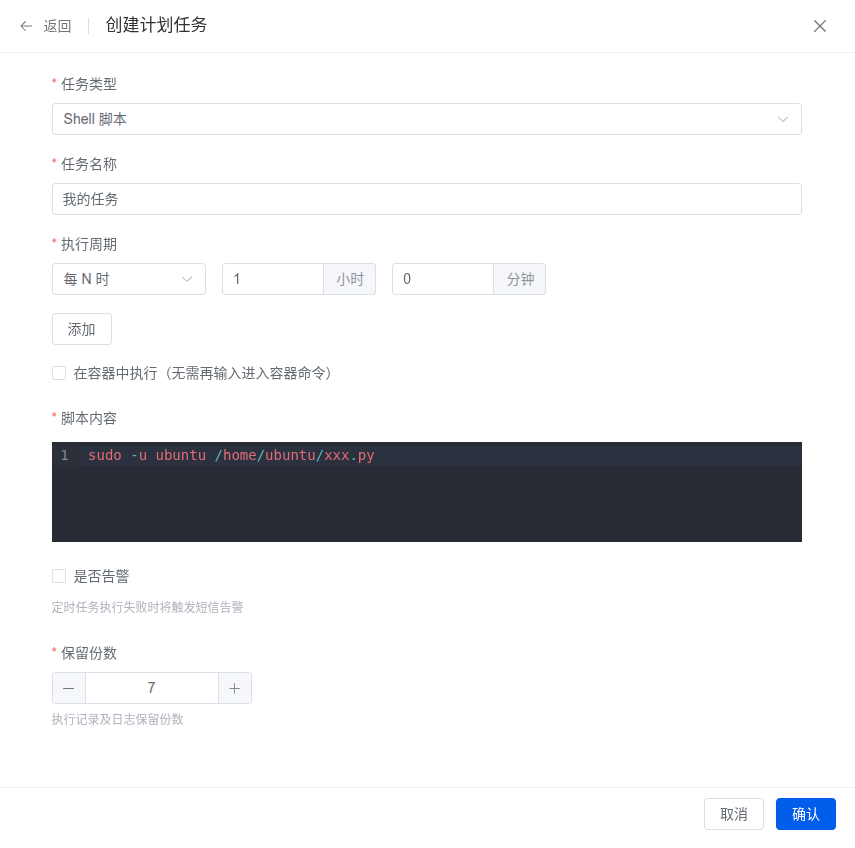
【Linux】使用1Panel 面板让服务器定时自动执行任务
服务器就是一台24小时开机的主机,相比自己家中不定时开关机的主机更适合完成定时任务,例如下载资源、备份上传,或者登录某个网站执行一些操作,只需要编写 脚本,然后让服务器定时来执行这个脚本就可以。 有很多方法实现…...
