PCA主成分分析算法
在数据分析中,如果特征太多,或者特征之间的相关性太高,通常可以用PCA来进行降维。比如通过对原有10个特征的线性组合, 我们找出3个主成分,就足以解释绝大多数的方差,该算法在高维数据集中被广泛应用。
算法(没时间看版本):
- 将数据标准化,即把所有数据转换以原点为中心;
- 划一条通过原点的直线,将所有点投影到该直线上,然后计算这些投影点到原点的距离平方和。设想我们不停的转动该直线,最终找到一条直线使得这个距离平方和最大,也就是该直线最接近所有的点,该直线为特征向量的方向,称为PC1,这个距离平方和即为特征值;
- 按同样的方法,找到第二条直线,该直线与PC1垂直且距离平方和最大,为PC2;
- 重复该过程直到找到所有的PC;
- 根据需求,确定头部的几个PC可以解释绝大多数方差。
下面先给出几个相关的概念。
协方差和散度矩阵
样本均值:
x ˉ = 1 n ∑ i = 1 N x i \bar{x} = \frac{1}{n} \sum_{i=1}^N x_i xˉ=n1i=1∑Nxi
样本方差:
S 2 = 1 n − 1 ∑ i = 1 n ( x i − x ˉ ) 2 S^2=\frac{1}{n-1} \sum_{i=1}^n {(x_i-\bar{x})}^2 S2=n−11i=1∑n(xi−xˉ)2
样本X和样本Y的协方差:
C o v ( X , Y ) = E [ ( X − E ( X ) ) ( Y − E ( Y ) ) ] = 1 n − 1 ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) Cov(X,Y)=E[(X-E(X))(Y-E(Y))]=\frac{1}{n-1}\sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y}) Cov(X,Y)=E[(X−E(X))(Y−E(Y))]=n−11i=1∑n(xi−xˉ)(yi−yˉ)
- 方差的计算是针对一维特征的,即针对同一特征不同样本的取值来进行计算得到;而协方差必须要求至少满足二维特征;方差是协方差的特殊情况。
- 方差和协方差的除数是 n − 1 n-1 n−1,这是为了得到方差和协方差的无偏估计。
协方差为正时,说明X和Y是正相关关系;为负时负相关关系;为0时相互独立。 C o v ( X , X ) Cov(X,X) Cov(X,X)就是X的方差。当样本是n维数据时,它们的协方差实际上是协方差矩阵(对称方阵)。
散度矩阵
S = ∑ k = 1 n ( x k − m ) ( x k − m ) T S=\sum_{k=1}^{n}(x_k-m)(x_k-m)^T S=k=1∑n(xk−m)(xk−m)T
其中 m = 1 n ∑ k = 1 n x k m=\frac{1}{n}\sum_{k=1}^{n}x_k m=n1∑k=1nxk
对于数据X的散度矩阵为 X X T XX^T XXT。其实协方差矩阵和散度矩阵关系密切,散度矩阵就是协方差矩阵乘以(总数据量-1)。因此它们的特征值和特征向量是一样的。同时散度矩阵是SVD奇异值分解的一步,因此PCA和SVD有密切关系。
特征值分解矩阵原理
- 特征值与特征向量
如果一个向量v是矩阵A的特征向量,则一定可以表示成下面的形式:
A v = λ v Av=\lambda v Av=λv
其中, λ \lambda λ是特征向量v对应的特征值,一个矩阵的一组特征向量是一组正交向量。 - 特征值分解矩阵
对于矩阵A,有一组特征向量v,将这组向量进行正交化单位化,就能得到一组正交单位向量。特征值分解,就是将矩阵A分解为如下式:
A = Q ∑ Q − 1 A=Q\sum Q^{-1} A=Q∑Q−1
其中,Q是矩阵A的特征向量组成的矩阵, ∑ \sum ∑则是一个对角阵,对角线上的元素就是特征值。
SVD分解矩阵原理
奇异值分解是一个能使用任意矩阵的一种分解的方法,对于任意矩阵A总是存在一个奇异值分解:
A = U ∑ V T A=U\sum V^T A=U∑VT
假设A是一个 m × n m\times n m×n矩阵,那么得到的U是一个 m × m m\times m m×m的方阵,U里面的正交向量被称为左奇异向量。 ∑ \sum ∑是一个 m × n m\times n m×n矩阵, ∑ \sum ∑除了对角线其他元素都为0.对角线上的元素称为奇异值。 V T V^T VT是V的转置矩阵,是一个 n × n n\times n n×n的方阵,它里面的正交向量被称为右奇异值向量。通常 ∑ \sum ∑上的值按从大到小的顺序排列。
SVD算法:
- 求 A A T AA^T AAT的特征值和特征向量,用单位化的特征向量构成U;
- 求 A T A A^TA ATA的特征值和特征向量,用单位化的特征向量构成V;
- 将 A A T AA^T AAT或者 A T A A^TA ATA的特征值求平方根,然后构成 ∑ \sum ∑。
基于特征值分解协方差矩阵实现PCA算法
输入:数据集 X = x 1 , x 2 , x 3 , . . . , x n X={x_1,x_2,x_3,...,x_n} X=x1,x2,x3,...,xn,需要降到k维。
1.去平均值(即去中心化),即每一位特征减去各自的平均值。
2.计算协方差矩阵 1 n X X T \frac{1}{n}XX^T n1XXT,注:这里除或不除样本数量 n n n或 n − 1 n-1 n−1,其实对求出的特征向量没有影响。
3.用特征值分解方法求协方差矩阵 1 n X X T \frac{1}{n}XX^T n1XXT的特征值与特征向量。
4.对特征值从大到小排序,选择其中最大的k个。然后将对应的k个特征向量分别作为行向量组成特征向量矩阵P。
5.将数据转换到k个特征向量构建的新空间中,即 Y = P X Y=PX Y=PX。
基于SVD分解协方差矩阵实现PCA算法
输入:数据集 X = x 1 , x 2 , x 3 , . . . , x n X={x_1,x_2,x_3,...,x_n} X=x1,x2,x3,...,xn,需要降到k维。
1.去平均值(即去中心化),即每一位特征减去各自的平均值。
2.计算协方差矩阵 1 n X X T \frac{1}{n}XX^T n1XXT,注:这里除或不除样本数量 n n n或 n − 1 n-1 n−1,其实对求出的特征向量没有影响。
3.用SVD分解方法求协方差矩阵 1 n X X T \frac{1}{n}XX^T n1XXT的特征值与特征向量。
4.对特征值从大到小排序,选择其中最大的k个。然后将对应的k个特征向量分别作为行向量组成特征向量矩阵。
5.将数据转换到k个特征向量构建的新空间中。
相关文章:

PCA主成分分析算法
在数据分析中,如果特征太多,或者特征之间的相关性太高,通常可以用PCA来进行降维。比如通过对原有10个特征的线性组合, 我们找出3个主成分,就足以解释绝大多数的方差,该算法在高维数据集中被广泛应用。 算法(…...
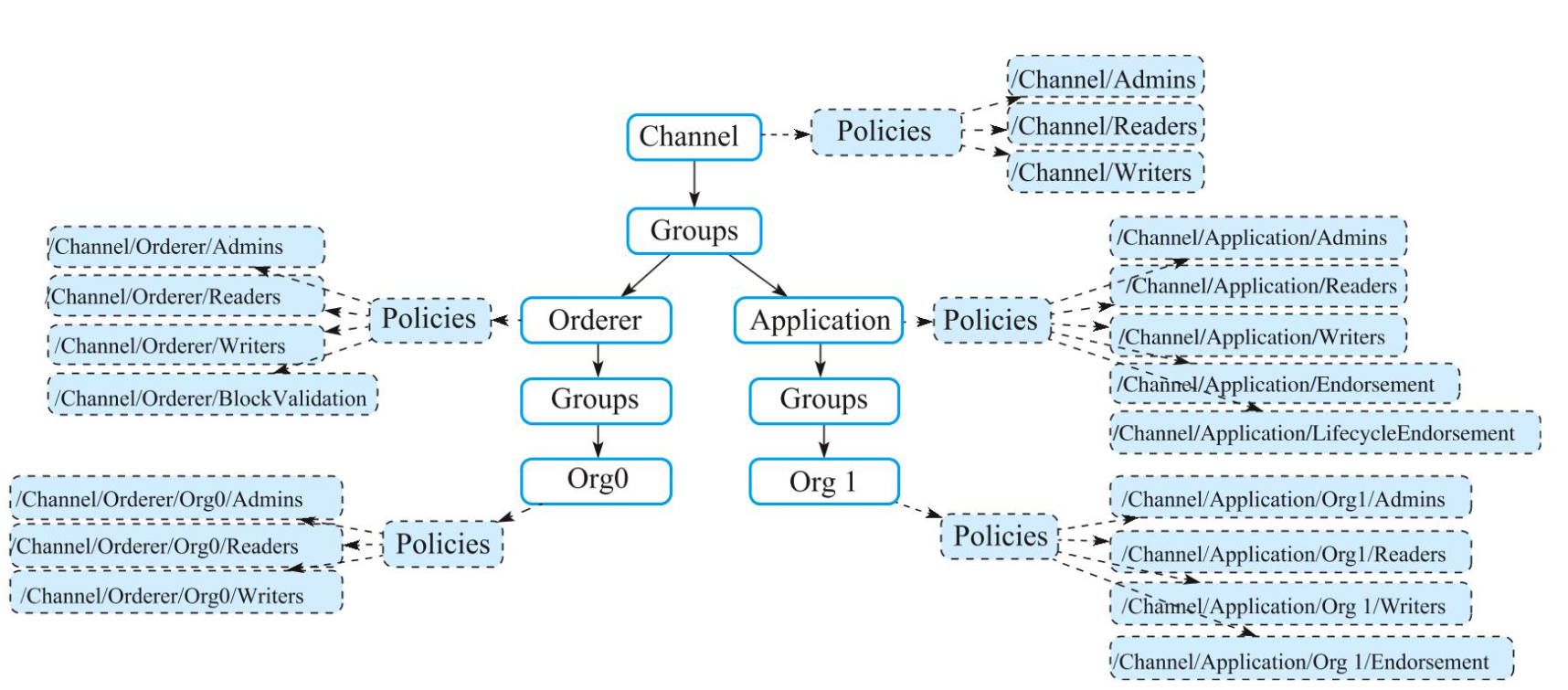
Hyperledger Fabric 权限策略和访问控制
访问控制是区块链网络十分重要的功能,负责控制某个身份在某个场景下是否允许采取某个操作(如读写某个资源)。 常见的访问控制模型包括强制访问控制(Mandatory Access Control)、自主访问控制(Discretionar…...

Day28 回溯算法part04 93. 复原IP地址 78. 子集 90. 子集 II
回溯算法part04 93. 复原IP地址 78. 子集 90. 子集 II 93. 复原 IP 地址 class Solution { private:vector<string> result;bool isValid(string& s,int start,int end){if (start > end) return false;if (s[start] 0 && start ! end) { // 0开头的数…...

Linux系统常用的安全优化
环境:CentOS7.9 1、禁用SELinux SELinux是美国国家安全局对于强制访问控制的实现 1)永久禁用SELinux vim /etc/selinux/config SELINUXdisabled #必须重启系统才能生效2)临时禁用SELInux getenforce #查看SELInux当前状态 setenforce 0 #数字…...
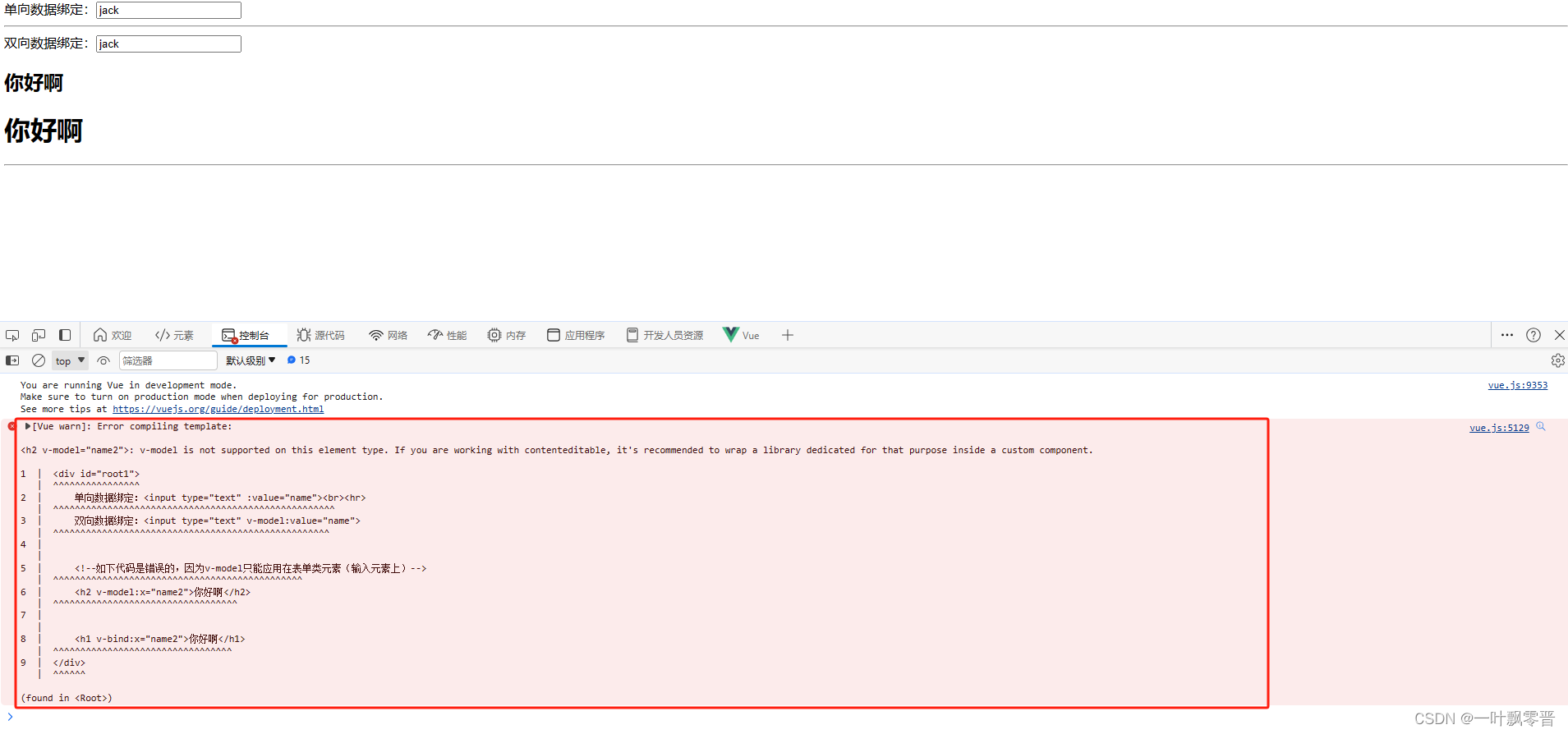
Vue-4、单向数据绑定与双向数据绑定
1、单向数据绑定 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>数据绑定</title><!--引入vue--><script type"text/javascript" src"https://cdn.jsdelivr.net/npm/…...

【Flutter 开发实战】Dart 基础篇:常用运算符
在Dart中,运算符是编写任何程序的基本构建块之一。本文将详细介绍Dart中常用的运算符,以帮助初学者更好地理解和运用这些概念。 1. 算术运算符 算术运算符用于执行基本的数学运算。Dart支持常见的加、减、乘、除、整除以及取余运算。常见的算数运算符如…...

C++:ifstream通过getline读取文件会忽略最后一行空行
getline是读取文件的常用函数,虽然使用简单,但是有一个较容易被忽视的问题,就是文件最后一行空行会被忽略。 #include <iostream> #include <fstream> #include <string> using namespace std;void readWholeFileWithGetline(string fileName) {string t…...

力扣123. 买卖股票的最佳时机 III
动态规划 思路: 最多可以完成两笔交易,因此任意一天结束后,会处于5种状态: 未进行任何操作;只进行了一次买操作;进行了一次买操作和一次卖操作;再完成了一次交易之后,进行了一次买操…...

Vue3:vue-cli项目创建
一、node.js检测或安装: node -v node.js官方 二、vue-cli安装: npm install -g vue/cli # OR yarn global add vue/cli/*如果安装的时候报错,可以尝试一下方法 删除C:\Users**\AppData\Roaming下的npm和npm-cache文件夹 删除项目下的node…...

C# .Net学习笔记—— 异步和多线程(Task)
一、概念 Task是DotNet3.0之后所推出的一种新的使用多线程的方式,它是基于ThreadPool线程进行封装的。 二、使用多线程的时机 任务能够并发运行的时候,提升速度;优化体验 三、基本使用方法 private void button5_Click(object sender, Ev…...
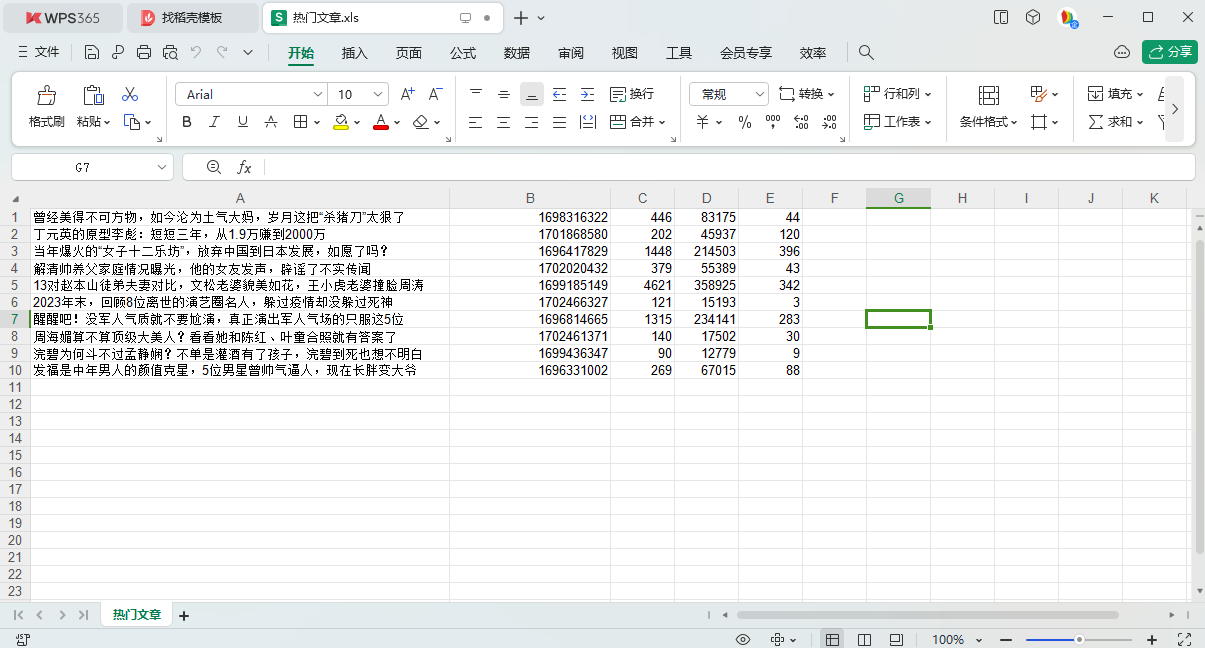
Python从入门到网络爬虫(读写Excel详解)
前言 Python操作Excel的模块有很多,并且各有优劣,不同模块支持的操作和文件类型也有不同。最常用的Excel处理库有xlrd、xlwt、xlutils、xlwings、openpyxl、pandas,下面是各个模块的支持情况: 工具名称.xls.xlsx获取文件内容写入…...
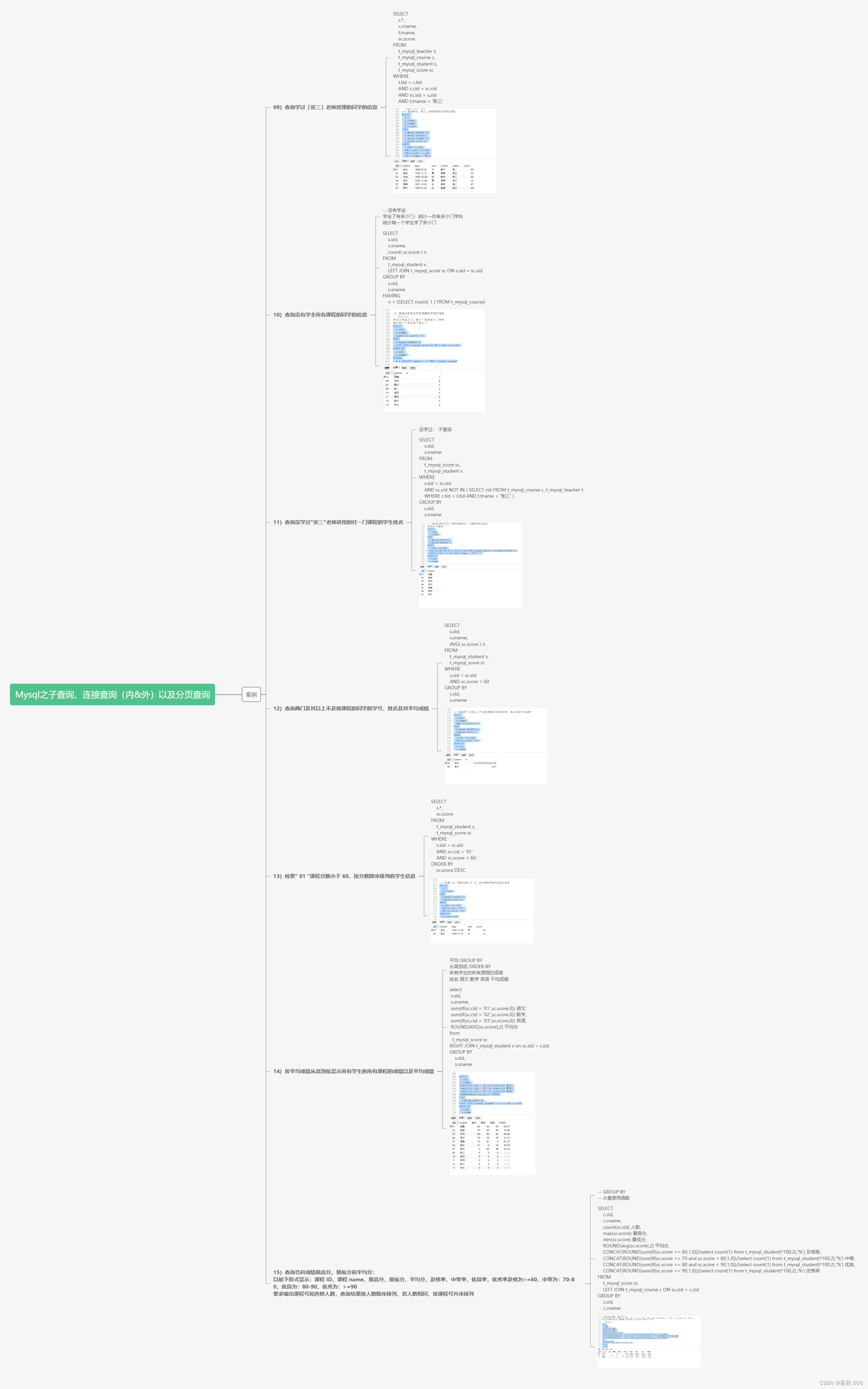
Mysql之子查询、连接查询(内外)以及分页查询
目录 一.案例(接上篇博客) 09)查询学过「张三」老师授课的同学的信息 10)查询没有学全所有课程的同学的信息 11)查询没学过"张三"老师讲授的任一门课程的学生姓名 12)查询两门及其以上不及格课程…...

计算机的存储单位
在计算机中,只能识别二进制。 byte是1个字节,是8个比特位,所以byte可以存储的最大值是:01111111,byte是 [-128 ~ 127] 共可以标识256个不同的数字。 1字节 8bit(8比特)--> 1byte 8bit 类…...

设备树文件中的设备节点
一. 简介 前面几篇文章学习了 关于设备树文件的编译,设备树文件的调用。 本文开始学习 设备树文件的语法。具体学习设备节点与标准属性。 二. 设备树文件之设备节点与标准属性 1. 设备节点 设备树 是采用树形结构来描述板子上的设备信息的文件,每…...

文件管理工具.netcore资源文件管理
文件管理工具 怎么快速有效的管理我的文件包括文件夹,需求功能是 模糊搜索显示匹配的文件夹或文件数据 快速打开文件夹位置 在windows直接查看搜索速度太慢,范围宽泛,整理所需资源文件名和文件本机路径保存在数据库,可以在数据库中…...

go-carbon v2.3.4 发布,轻量级、语义化、对开发者友好的 Golang 时间处理库
carbon 是一个轻量级、语义化、对开发者友好的 golang 时间处理库,支持链式调用。 目前已被 awesome-go 收录,如果您觉得不错,请给个 star 吧 github.com/golang-module/carbon gitee.com/golang-module/carbon 安装使用 Golang 版本大于…...

vue3 内置组件
文章目录 前言一、过渡效果相关的组件1、Transition2、TransitionGroup 二、状态缓存组件(KeepAlive)三、传送组件(Teleport )四、异步依赖处理组件(Suspense) 前言 在vue3中 其提供了5个内置组件 Transiti…...

MFC如何动态创建button按钮并添加点击事件
在MFC中,可以使用CButton类来动态创建按钮。下面是一个示例代码,演示了如何动态创建按钮并添加点击事件: 在对话框类的头文件中声明按钮变量: CButton m_btnDynamic;在对话框的OnInitDialog()函数中使用Create()函数创建按钮&am…...
Qt - QML框架
文章目录 1 . 前言2 . 框架生成3 . 框架解析3.1 qml.pro解析3.2 main.cpp解析3.3 main.qml解析 4 . 总结 【极客技术传送门】 : https://blog.csdn.net/Engineer_LU/article/details/135149485 1 . 前言 什么是QML? QML是一种用户界面规范和编程语言。它允许开发人员…...
Python+Flask+MySQL的图书馆管理系统【附源码,运行简单】
PythonFlaskMySQL的图书馆管理系统【附源码,运行简单】 总览 1、《的图书馆管理系统》1.1 方案设计说明书设计目标需求分析工具列表 2、详细设计2.1 登录2.2 注册2.3 程序主页面2.4 图书新增界面2.5 图书信息修改界面2.6 普通用户界面2.7 其他功能贴图 3、下载 总览…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...

6.计算机网络核心知识点精要手册
计算机网络核心知识点精要手册 1.协议基础篇 网络协议三要素 语法:数据与控制信息的结构或格式,如同语言中的语法规则语义:控制信息的具体含义和响应方式,规定通信双方"说什么"同步:事件执行的顺序与时序…...

02-性能方案设计
需求分析与测试设计 根据具体的性能测试需求,确定测试类型,以及压测的模块(web/mysql/redis/系统整体)前期要与相关人员充分沟通,初步确定压测方案及具体的性能指标QA完成性能测试设计后,需产出测试方案文档发送邮件到项目组&…...
