3D模型UV展开原理
今年早些时候,我为 MAKE 杂志写了一篇教程,介绍如何制作视频游戏角色的毛绒动物。 该技术采用给定的角色 3D 模型及其纹理,并以编程方式生成缝纫图案。 虽然我已经编写了一般摘要并将源代码上传到 GitHub,但我在这里编写了对使这一切成为可能的数学的更深入的解释。
NSDT工具推荐: Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 可编程3D场景编辑器 - REVIT导出3D模型插件 - 3D模型语义搜索引擎
我的项目目标是创建一个可打印的缝纫图案,一旦缝合在一起,就会接近起始 3D 模型(在本例中为视频游戏角色)。 我的技术要点是使用 3D 模型的纹理图像文件作为缝纫图案。 纹理图像应该能够在其 UV 接缝处连接以重建原始 3D 形状。 3D 模型的初始纹理图像可能未针对缝合重建进行优化,但可以通过从原始模型创建一组新的 UV(接缝针对缝合进行了更优化)来进行补救。 给定原始 UV 和新 UV,可以为每个面计算变换矩阵,以将旧纹理图像变换为新的优化纹理图像。 缝合重建的分辨率取决于接缝的位置和 UV 展开算法的变形量。
如一般摘要中所述,3D 模型由几个不同的特征组成。 它具有定义其 3D 形状的顶点、边和面。 它还具有一组 UV 坐标,用于定义纹理如何投影到每个面上。 最后,它具有定义 3D 模型着色方式的纹理图像。

UV 映射是将 3D 面投影到 2D 纹理表面的过程,在计算机图形学领域得到了很好的研究。 3D 模型的每个面都映射到 UV 贴图上的一个面。 UV贴图上的每个面对应3D模型上的一个面,UV保留了3D模型的面之间的边缘关系。 筑波大学的 Yuki Igarashi 博士意识到了 UV 的这一特性,并在她的论文 Plushie: An Interactive Design System for Plush Toys (SIGGRAPH 2006) 和Pillow: Interactive Flattening of a 3D Model for Plush Toy Design(SIGGRAPH 2007) 中使用 UV 从动态创建的 3D 模型中创建缝纫图案。 她的UV贴图的具体算法是ABF++。
由于 UV 贴图可以用作缝纫图案,因此纹理图像也可以,因为 UV 将纹理图像映射到 3D 模型上。 纹理可以打印到织物上,并且根据图案缝制而成的毛绒动物将保留原始 3D 模型的颜色信息。
然而,并非每个 UV 贴图都针对缝纫图案创建进行了优化。 正如你在上面看到的,UV 相互折叠,因此 UV 和主体减半。 这是视频游戏图形中一种流行的节省空间的技术。 头部也比身体大得多,因此在视频游戏中头部会显得有更精细的细节。 这些优化不适合缝纫图案,因为我们希望身体在 3D 空间中的比例与 2D UV 空间中的比例大致相同。

最终分辨率的差异, 来自Igarashi
UV 簇的接缝将成为最终毛绒动物上的接缝。 从相同的 3D 模型开始,接缝位置将决定最终缝制作品的分辨率。
我的模型的初始 UV 不适合毛绒动物创作,因此我制作了自己的 UV,以优化它们以进行缝纫。 大多数现代 3D 图形软件都具有 UV 映射功能(Maya、Blender、3ds Max 等)。 在我的项目中,我使用了 UVLayout,这是一种专门的 UV 映射工具,但正如 MAKE 杂志文章中所见,Blender 也能正常工作。
我最终的 UV 贴图的一部分
有了新创建的 UV 贴图,我想创建一个与其相对应的新纹理贴图,并将其打印为我的最终缝纫图案。 这就是线性代数派上用场的地方。
UV 贴图上的多边形面被分解为三角形。 旧的原始 UV 上的每个三角形面通过它们与 3D 模型上同一面的关系映射到新 UV 上的三角形。 由于两个三角形代表相同的形状,但在 UV 贴图上具有不同的坐标,因此可以计算两个三角形之间的变换矩阵。 使用三角形是因为我们想要使用方阵进行计算。 该变换矩阵可用于变换旧纹理上的相应三角形区域,以对新纹理上的新三角形区域进行着色。 Stackoverflow 对如何根据两个三角形的坐标计算变换矩阵以及我使用的有用代码片段进行了很好的解释。
如果计算每个 UV 三角形的变换矩阵并变换其相应的纹理三角形,最终结果将是一个新的纹理。 如果将新纹理和新 UV 应用到原始 3D 模型,其视觉外观应该不会有任何差异。
在我的实现中,首先将 UV 坐标映射到纹理图像上的像素坐标,然后计算变换矩阵。 映射(与浮点不精确相结合)导致了一些舍入问题(因为像素坐标必须是整数),这在求解变换矩阵期间导致了奇异矩阵。 我的黑客解决方案是将 UV 点之一的像素坐标之一偏移 1 个像素。 我认为最终打印图案上的 1 个像素不太明显。
例如:
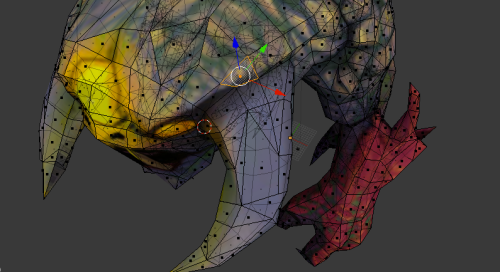
上面是 3D 模型,突出显示的脸部是感兴趣的脸部。

对应于原始 UV 贴图上的面,其 UV 坐标为 (0.7153, -0.2275)、(0.78, -0.1982)、(0.7519, -0.0935)、(0.7207, -0.0382)。

正如你所看到的,UV 将纹理图像映射到 3D 模型。

该特定的 UV 面控制纹理图像上的一小部分。

3D 模型上突出显示的面也对应于我创建的新 UV 贴图上的面。
其坐标为 (0.046143, 0.63782)、(0.133411, 0.683826)、(0.09056, 0.660572)、(0.108221, 0.6849)。
给定两组 UV 坐标,我将 UV 四边形分解为两个三角形并计算变换矩阵。
为了计算变换矩阵,建立方程如下:
![]()
其中 W 是包含新 UV 坐标的矩阵,A 是变换矩阵,Z 是包含旧 UV 坐标的矩阵。
由于使用齐次坐标,W和Z是3×3方阵,最后一行为[1 1 1],A也是3×3方阵,最后一行为[0 0 1]。有关更多详细信息,请参阅仿射变换。
用实际坐标填充我们的矩阵给出以下两个方程。 原始 UV 坐标映射到像素坐标 (384, 72)、(396, 80)、(401, 67)、(383, 61)。 新的 UV 坐标映射到 (29, 174)、(23, 185)、(33, 188)、(35, 172)。 我使用像素坐标进行转换。

如前所述,有两个方程,因为我将四边形分成两个三角形。
为了求解 A,我可以取 Z 的倒数并将其乘以 W。由于 Z 是方阵,因此 Z 是可逆的,因为它的行列式不为零。 Z 的行列式不为零,因为行列式表示它所包围的三角形的面积。
![]()
![]()
然而,在实际实现中,我以更直接的方式解决了这个问题,即进行A和Z之间的矩阵乘法并求解未知数系统。 在这里相关信息。
当应用于原始 UV 控制的纹理图像区域时,我得到以下转换后的纹理图像片段:

转换每个纹理图像区域后,你将获得以下可以打印的纹理图像。橙色箭头表示变换后的纹理块适合整个纹理图像的位置。

这就是如何从 3D 模型创建缝纫图案的更理论/数学解释。
原文链接:3D展2D数学原理 - BimAnt
相关文章:

3D模型UV展开原理
今年早些时候,我为 MAKE 杂志写了一篇教程,介绍如何制作视频游戏角色的毛绒动物。 该技术采用给定的角色 3D 模型及其纹理,并以编程方式生成缝纫图案。 虽然我已经编写了一般摘要并将源代码上传到 GitHub,但我在这里编写了对使这一…...
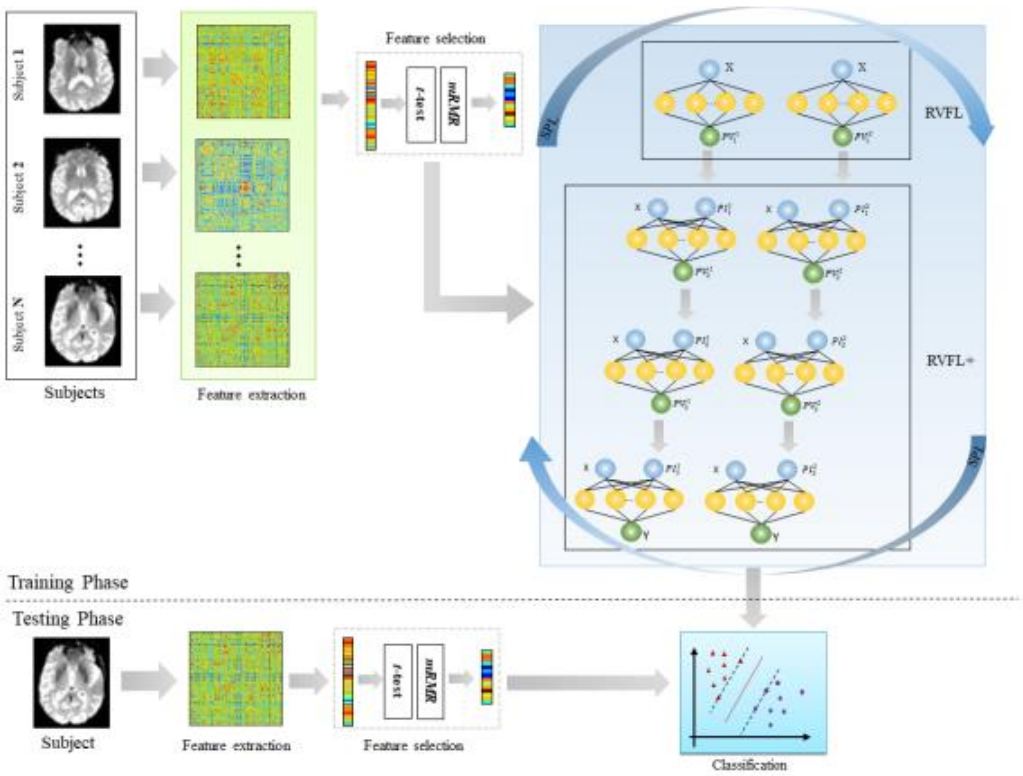
SPL-cmcRVFL+
吐槽 作者未提供代码,还有图1敢再糊点吗?...

Vue3+TS+Vite 构建自动导入开发环境
关注⬆️⬆️⬆️⬆️ 专栏后期更新更多前端内容 在一个使用 Vue 3、Vite 和 TypeScript 的项目中,配置 unplugin-auto-import 和 unplugin-vue-components 插件可以极大地提高开发效率,因为它们可以自动导入 Vue 相关的 API 和 Vue 组件,从而减少了手动导入的需要。 文章目…...
长期使用外接键盘,外物压着自带键盘,容易导致华硕飞行堡垒FX53VD键盘全部失灵【除电源键】
华硕飞行堡垒FX53VD键盘全部失灵【除电源键】 前言一、故障排查二、发现问题三、使用方法总结 前言 版本型号: 型号 ASUS FX53VD(华硕-飞行堡垒) 板号:GL553VD 故障情况描述: 键盘无法使用,键盘除开机键外…...

JavaScript-循环嵌套断点调试-笔记
1.do...while循环 do while语法结构: 循环初始值; do{ //代码; 增量; }while(循环条件); <script> // 输出十句 : 你好世界 var …...
1042: 数列求和3 和 1057: 素数判定 和 1063: 最大公约与最小公倍
1042: 数列求和3 题目描述 求1-2/33/5-4/75/9-6/11...的前n项和,结果保留3位小数。 输入 输入正整数n(n>0)。 输出 输出一个实数,保留3位小数,单独占一行。 样例输入 5 样例输出 0.917 #include<stdio.h> int main(){in…...

[足式机器人]Part2 Dr. CAN学习笔记-动态系统建模与分析 Ch02-8 Bode Plot伯德图
本文仅供学习使用 本文参考: B站:DR_CAN Dr. CAN学习笔记-动态系统建模与分析 Ch02-8 Bode Plot伯德图 Bode Plot 手绘技巧与应用...
Java 将Excel转换为TXT文本格式
TXT文件是一种非常简单、通用且易于处理的文本格式。在处理大规模数据时,将Excel转为TXT纯文本文件可以提高处理效率。此外,许多编程语言和数据处理工具都有内置的函数和库来读取和处理TXT文件,因此将Excel文件转换为TXT还可以简化数据导入过…...

什么事“网络水军”?他们的违法活动主要有四种形式
我国治理网络水军,包括造谣引流、舆情敲诈、刷量控评、有偿删帖等各类“网络水军”等违法犯罪活动已经许久。 日前,官方召开新闻发布会,公布了相关的一些案件进程,今年已累计侦办相关案件339起,超过历年的全年侦办案件…...
)
授权策略(authorize方法)
authorize方法(授权策略的使用示例) $this->authorize(destroy, $status) 要实现这个功能,你需要执行以下步骤: 1、创建一个授权策略: 在Laravel中,授权策略是用于定义用户对特定操作的权限的类。你可…...
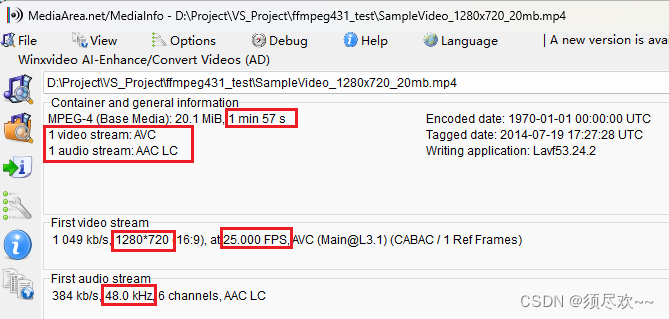
FFmpeg获取音视频流信息
文章目录 前言一、需求二、源码三、运行结果 前言 本文记录用 FFmpeg 获取视频流音频流的信息(编码格式、分辨率、帧率、播放时长…),所用的工程基于上个博客编译成功的工程:使用FFmpeg4.3.1的SDK官方开发包编译ffmpeg.c 一、需求…...

编程语言的走向又将如何呢?
编程语言的未来? 随着科技的飞速发展,编程语言在计算机领域中扮演着至关重要的角色。它们是软件开发的核心,为程序员提供了与机器沟通的桥梁。那么,在技术不断进步的未来,编程语言的走向又将如何呢? 1. 更…...

基于SpringBoot的电影评论网站
文章目录 项目介绍主要功能截图:部分代码展示设计总结项目获取方式🍅 作者主页:超级无敌暴龙战士塔塔开 🍅 简介:Java领域优质创作者🏆、 简历模板、学习资料、面试题库【关注我,都给你】 🍅文末获取源码联系🍅 项目介绍 基于SpringBoot的电影评论网站,java项目…...

粒子群算法优化支持向量SVM的供热量预测,粒子群优化支持向量机SVM回归分析
目录 背影 支持向量机SVM的详细原理 SVM的定义 SVM理论 粒子群算法原理 SVM应用实例,粒子群算法优化支持向量SVM的供热量预测,粒子群优化支持向量机SVM回归分析 代码 结果分析 展望 完整代码:粒子群算法优化支持向量SVM的供热量预测,粒子群优化支持向量机SVM回归分析_lssv…...
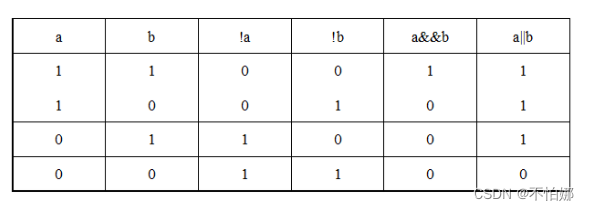
【Verilog】运算符
系列文章 数值(整数,实数,字符串)与数据类型(wire、reg、mem、parameter) 系列文章算术运算符关系运算符相等关系运算符逻辑运算符按位运算符归约运算符移位运算符条件运算符连接和复制运算符 算术运算符 …...

浅析ARMv8体系结构:A64指令集
文章目录 A64指令编码格式加载与存储指令寻址模式变基模式前变基模式后变基模式 PC相对地址模式 伪指令加载与存储指令的变种不同位宽的加载与存储指令多字节内存加载和存储指令基地址偏移量模式前变基模式后变基模式 跳转指令返回指令比较并跳转指令 其它指令内存独占访问指令…...

VSCode安装GitHub Copilot插件方法
VSCode安装GitHub Copilot插件的步骤及注意事项如下: 安装步骤: 确保系统要求: 确保你正在使用的Visual Studio Code版本是最新的,且支持GitHub Copilot。同时,Copilot需要你的操作系统是Windows、macOS或Linux&#x…...

实战:使用docker容器化服务
本文介绍使用docker安装mysql和redis,通过这两个的实战,了解一般的安装容器化服务的流程,体会服务容器化的好处 1.使用docker安装MySQL docker 拉取 mysql 镜像 docker pull mysql:5.7运行 mysql 镜像 docker run -p 3306:3306 --name mysql…...
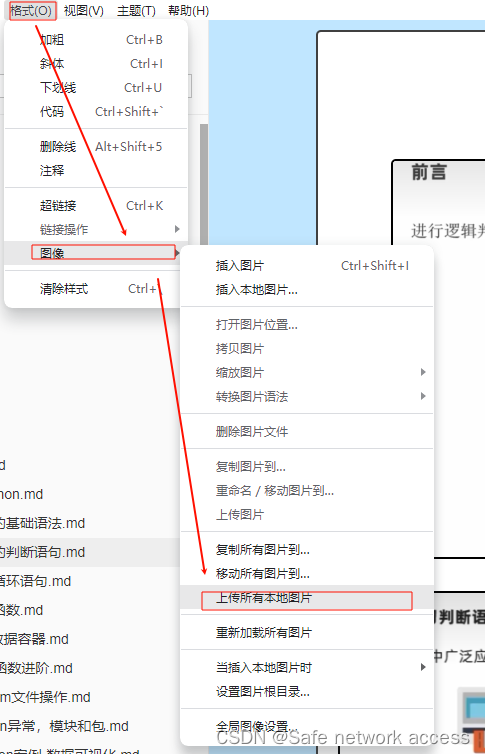
借用GitHub将typora图片文件快速上传CSDN
前情概要 众所周知,程序员大佬们喜欢用typora软件写代码笔记,写了很多笔记想要放到CSDN上给其他大佬分享,但是在往csdn上搬运的时候,图片总是上传出错,一张一张搞有很麻烦,咋如何搞? 废话不多…...
外包公司干了2个月,技术退步明显了.......
先说一下自己的情况,本科毕业,18年通过校招进入南京某软件公司,干了接近4年的功能测试,今年年初,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落! 而我已经在一个企业干了四年的功能…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...

二维FDTD算法仿真
二维FDTD算法仿真,并带完全匹配层,输入波形为高斯波、平面波 FDTD_二维/FDTD.zip , 6075 FDTD_二维/FDTD_31.m , 1029 FDTD_二维/FDTD_32.m , 2806 FDTD_二维/FDTD_33.m , 3782 FDTD_二维/FDTD_34.m , 4182 FDTD_二维/FDTD_35.m , 4793...

Django RBAC项目后端实战 - 03 DRF权限控制实现
项目背景 在上一篇文章中,我们完成了JWT认证系统的集成。本篇文章将实现基于Redis的RBAC权限控制系统,为系统提供细粒度的权限控制。 开发目标 实现基于Redis的权限缓存机制开发DRF权限控制类实现权限管理API配置权限白名单 前置配置 在开始开发权限…...
