mysql 添加用户并分配select权限
1.root用户先登录或者在可执行界面
1.1 选择mysql
点击mysql 或者在命令行 use mysql
1.2创建用户
CREATE USER 'username'@'%' IDENTIFIED BY 'password';

备注1:%替换为可访问数据库的ip,例如“127.0.0.1”“192.168.1.1”,使用“%”表示不限制远程连接ip
备注2:username可修改:为登录的用户名;password可修改:为登录的密码
1.3 查看用户
SELECT * FROM user;
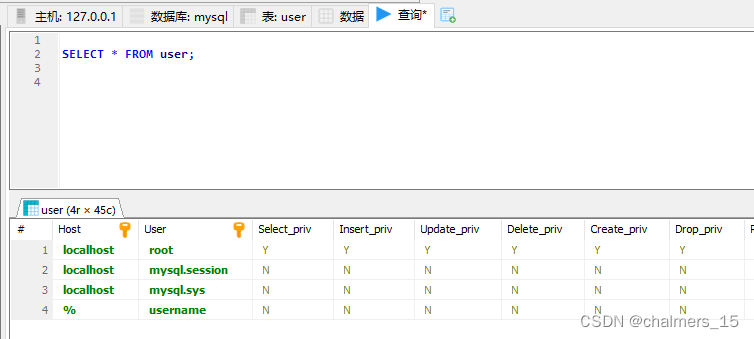
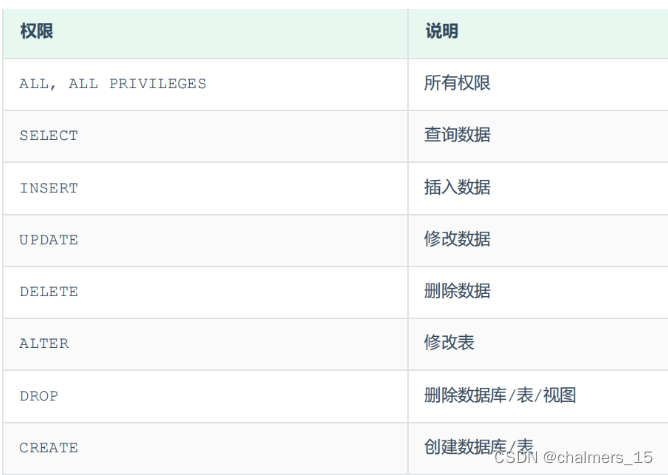
1.4 给权限
GRANT select ON xl_game3.* TO 'username'@'%';

备注:select 可用其他的来替换
1.5刷新
FLUSH PRIVILEGES;
2.用户信息修改
2.1 修改用户密码
ALTER USER 'username'@'%' IDENTIFIED WITH mysql_native_password BY '123456' ;

2.2 删除用户
DROP user 'username'@'%' ;

3.用新增的账号登录
3.1 账号密码
3.2 只能查看到有权限的表
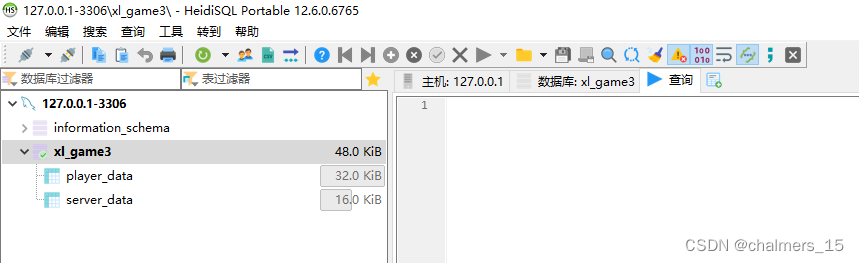
3.3 删除提示没权限

4.修改用户权限
4.1 查询权限
SHOW GRANTS FOR 'username'@'%'

4.2 新增权限
GRANT insert ON xl_game3.* TO 'username'@'%';

再次查询 SHOW GRANTS FOR 'username'@'%'
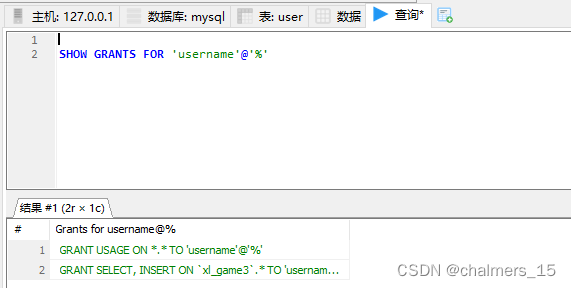
4.3 删除权限
REVOKE INSERT ON xl_game3.* FROM 'username'@'%'
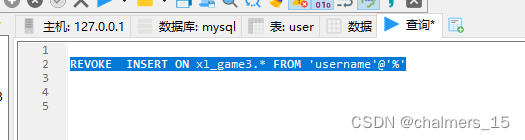
再次查询 SHOW GRANTS FOR 'username'@'%'

相关文章:

mysql 添加用户并分配select权限
1.root用户先登录或者在可执行界面 1.1 选择mysql 点击mysql 或者在命令行 use mysql 1.2创建用户 CREATE USER username% IDENTIFIED BY password; 备注1:%替换为可访问数据库的ip,例如“127.0.0.1”“192.168.1.1”,使用“%”表示不限制…...

重新认识canvas,掌握必要的联结密码
查看专栏目录 canvas示例教程100专栏,提供canvas的基础知识,高级动画,相关应用扩展等信息。canvas作为html的一部分,是图像图标地图可视化的一个重要的基础,学好了canvas,在其他的一些应用上将会起到非常重…...
Linux第21步_取消鼠标中键的复制粘贴功能
在ubuntu18.04操作系统中,选中文本后,若按下鼠标中键,就可以执行复制粘贴,相当于 CtrlshiftC 后又按了 CtrlshiftV。在Linux系统中,基本上都是这么配置的。在windows系统中,我们习惯用Ctrl-C复制࿰…...
数学建模-Matlab R2022a安装步骤
软件介绍 MATLAB是一款商业数学软件,用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境,主要包括MATLAB和Simulink两大部分,可以进行矩阵运算、绘制函数和数据、实现算法、创建用户界面、连接其他编程语言的程…...

【AI】Pytorch 系列:学习率设置
a. 有序调整:等间隔调整(Step),按需调整学习率(MultiStep),指数衰减调整(Exponential)和 余弦退火CosineAnnealing。 b. 自适应调整:自适应调整学习率 ReduceLROnPlateau。 c. 自定义调整:自定义调整学习率 LambdaLR。 #得到当前学习率 lr = next(iter(optimizer.param_gr…...

LeetCode第107题 - 二叉树的层序遍历 II
题目 解答 class Solution {List<List<Integer>> nodeLevels new LinkedList<>();public List<List<Integer>> levelOrderBottom(TreeNode root) {levelOrder(root, 0);List<List<Integer>> nodeLevels2 new LinkedList<>…...

java 常⽤的线程池模式FixedThreadPool
java 常⽤的线程池模式FixedThreadPool 线程池中的线程数量是固定的。 当提交一个新任务时,如果线程池中的线程都在运行,新任务就会被放入任务队列中等待执行。 如果线程池中的所有线程都在运行,且任务队列已满,那么线程池会创建新…...

双机调度算法
假设当前有两个处理机A、B,以及n个待处理的任务。第i个任务在处理处理机A上处理需要的时间为ai,在处理机B上处理的时间为bi,两个处理机可以并行处理任务,但单个处理机不能同时执行任务。要求给定n个任务及各个任务对应的ai 、bi&a…...

精进单元测试技能——Pytest断言的艺术
本篇文章主要是阐述Pytest在断言方面的应用。让大家能够了解和掌握Pytest针对断言设计了多种功能以适应在不同测试场景上使用。 了解断言的基础 在Pytest中,断言是通过 assert 语句来实现的。简单的断言通常用于验证预期值和实际值是否相等,例如…...

探索人工智能:深度学习、人工智能安全和人工智能
深度学习是人工智能的一种重要技术,它模拟了人类大脑神经网络的工作原理,通过建立多层次的神经元网络来实现对数据的分析和处理。这种技术的引入使得人工智能的发展进入到了一个新的阶段。 现如今,深度学习在各个领域都有着广泛的应用。例如…...
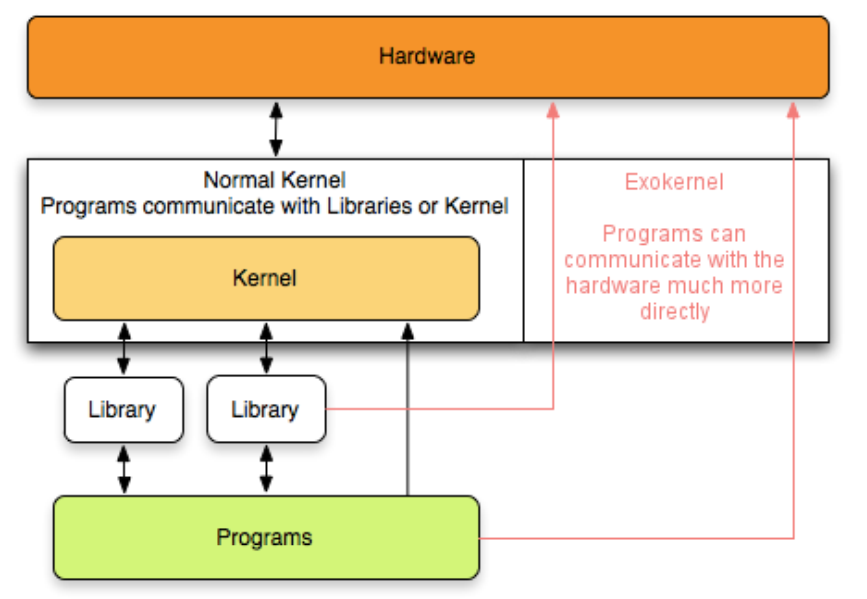
CHS_02.1.4+操作系统体系结构 二
CHS_02.1.4操作系统体系结构 二 操作系统的结构 上篇文章我们只介绍过宏内核 也就是大内核以及微内核分层结构的操作系统模块化是一种很经典的程序设计思想宏内核和微内核外核 操作系统的结构 上篇文章我们只介绍过宏内核 也就是大内核以及微内核 今年大纲又增加了分层结构 模块…...
【python可视化大屏】使用python实现可拖拽数据可视化大屏
介绍: 我在前几期分享了关于爬取weibo评论的爬虫,同时也分享了如何去进行数据可视化的操作。但是之前的可视化都是单独的,没有办法在一个界面上展示的。这样一来呢,大家在看的时候其实是很不方便的,就是没有办法一目了…...
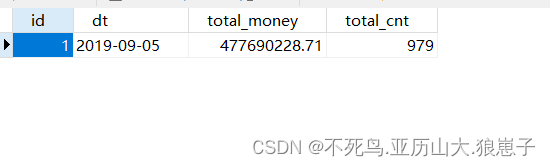
FineBI实战项目一(4):指标分析之每日订单总额/总笔数
1 明确数据分析目标 统计每天的订单总金额及订单总笔数 2 创建用于保存数据分析结果的表 use finebi_shop_bi;create table app_order_total(id int primary key auto_increment,dt date,total_money double,total_cnt int ); 3 编写SQL语句进行数据分析 selectsubstring(c…...

如何确定CUDA对应的pytorch版本?
参考:此链接...
分布式锁3: zk实现分布式锁5 使用中间件curator
一 curator的说明 1.1 curator的说明 curator是netflix公司开源的一个zk客户端。对Zookeeper提供的原生客户端进行封装,简化了Zookeeper客户端的开发量。Curator解决了很多zookeeper客户端非常底层的细节开发工作,包括连接重连、反复注册wathcer和Node…...
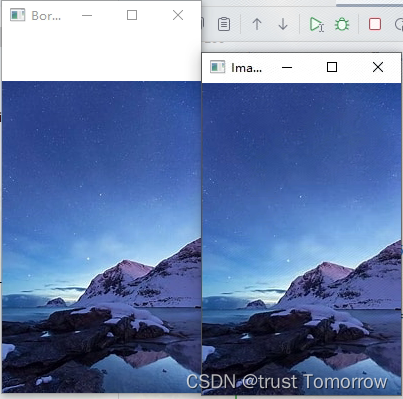
扩展边界opencv
扩展图像的边缘(如上边增加50像素)通常是通过添加额外的像素行来实现的 使用cv2.copyMakeBorder函数 valueborder_color指定了边框的颜色 import cv2 import numpy as np# 读取图像 image cv2.imread(th.jpg)# 设置边框宽度 top_border_width 50 # …...

开源C语言库Melon:Cron格式解析
本文介绍开源C语言库Melon的cron格式解析。 关于 Melon 库,这是一个开源的 C 语言库,它具有:开箱即用、无第三方依赖、安装部署简单、中英文文档齐全等优势。 Github repo 简介 cron也就是我们常说的Crontab中的时间格式,格式如…...

vue的学习方法
学习Vue.js的方法如下: 先了解基本概念和语法:学习Vue.js的第一步是了解它的基本概念,例如组件、指令、数据绑定等。你可以开始阅读Vue官方文档并参考教程和示例来掌握这些基本概念和语法。 实践项目:在理解了Vue.js的基本概念和…...

Hive之set参数大全-2
C 指定是否启用表达式缓存的评估 hive.cache.expr.evaluation 是 Hive 中的一个配置属性,用于指定是否启用表达式缓存的评估。表达式缓存是一项优化技术,它可以在执行查询时缓存表达式的评估结果,以减少计算开销。 在 Hive 配置中…...

C++面试宝典第17题:找规律填数
题目 仔细观察下面的数字序列,找到规律,并填写空白处的数字。 (1)1, 2, 4, 7, 11, 16, __ (2)-1, 2, 7, 28, __, 126 (3)6, 10, 18, 32, 57, __ (4)19, 6, 1, 2, 11, __ (5)2, 3, 5, 7, 11, __ (6)1, 8, 9, 4, __, 1/6 (7)1, 2, 3, 7, 16, __, 321 (8)1, 2, …...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件,这个上传文件是整体功能的一部分,文件在上传的过程中…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...

基于小程序老人监护管理系统源码数据库文档
摘 要 近年来,随着我国人口老龄化问题日益严重,独居和居住养老机构的的老年人数量越来越多。而随着老年人数量的逐步增长,随之而来的是日益突出的老年人问题,尤其是老年人的健康问题,尤其是老年人产生健康问题后&…...