NOIP2012提高组day1-T3:开车旅行
题目链接
[NOIP2012 提高组] 开车旅行
题目描述
小 A \text{A} A 和小 B \text{B} B 决定利用假期外出旅行,他们将想去的城市从 1 1 1 到 n n n 编号,且编号较小的城市在编号较大的城市的西边,已知各个城市的海拔高度互不相同,记城市 i i i 的海拔高度为 h i h_i hi,城市 i i i 和城市 j j j 之间的距离 d i , j d_{i,j} di,j 恰好是这两个城市海拔高度之差的绝对值,即 d i , j = ∣ h i − h j ∣ d_{i,j}=|h_i-h_j| di,j=∣hi−hj∣。
旅行过程中,小 A \text{A} A 和小 B \text{B} B 轮流开车,第一天小 A \text{A} A 开车,之后每天轮换一次。他们计划选择一个城市 s s s 作为起点,一直向东行驶,并且最多行驶 x x x 公里就结束旅行。
小 A \text{A} A 和小 B \text{B} B 的驾驶风格不同,小 B \text{B} B 总是沿着前进方向选择一个最近的城市作为目的地,而小 A \text{A} A 总是沿着前进方向选择第二近的城市作为目的地(注意:本题中如果当前城市到两个城市的距离相同,则认为离海拔低的那个城市更近)。如果其中任何一人无法按照自己的原则选择目的城市,或者到达目的地会使行驶的总距离超出 x x x 公里,他们就会结束旅行。
在启程之前,小 A \text{A} A 想知道两个问题:
1、 对于一个给定的 x = x 0 x=x_0 x=x0,从哪一个城市出发,小 A \text{A} A 开车行驶的路程总数与小 B \text{B} B 行驶的路程总数的比值最小(如果小 B \text{B} B 的行驶路程为 0 0 0,此时的比值可视为无穷大,且两个无穷大视为相等)。如果从多个城市出发,小 A \text{A} A 开车行驶的路程总数与小 B \text{B} B 行驶的路程总数的比值都最小,则输出海拔最高的那个城市。
2、对任意给定的 x = x i x=x_i x=xi 和出发城市 s i s_i si,小 A \text{A} A 开车行驶的路程总数以及小 B \text B B 行驶的路程总数。
输入格式
第一行包含一个整数 n n n,表示城市的数目。
第二行有 n n n 个整数,每两个整数之间用一个空格隔开,依次表示城市 1 1 1 到城市 n n n 的海拔高度,即 h 1 , h 2 . . . h n h_1,h_2 ... h_n h1,h2...hn,且每个 h i h_i hi 都是互不相同的。
第三行包含一个整数 x 0 x_0 x0。
第四行为一个整数 m m m,表示给定 m m m 组 s i s_i si 和 x i x_i xi。
接下来的 m m m 行,每行包含 2 2 2 个整数 s i s_i si 和 x i x_i xi,表示从城市 s i s_i si 出发,最多行驶 x i x_i xi 公里。
输出格式
输出共 m + 1 m+1 m+1 行。
第一行包含一个整数 s 0 s_0 s0,表示对于给定的 x 0 x_0 x0,从编号为 s 0 s_0 s0 的城市出发,小 A \text A A 开车行驶的路程总数与小 B \text B B 行驶的路程总数的比值最小。
接下来的 m m m 行,每行包含 2 2 2 个整数,之间用一个空格隔开,依次表示在给定的 s i s_i si 和 x i x_i xi 下小 A \text A A 行驶的里程总数和小 B \text B B 行驶的里程总数。
样例 #1
样例输入 #1
4
2 3 1 4
3
4
1 3
2 3
3 3
4 3
样例输出 #1
1
1 1
2 0
0 0
0 0
样例 #2
样例输入 #2
10
4 5 6 1 2 3 7 8 9 10
7
10
1 7
2 7
3 7
4 7
5 7
6 7
7 7
8 7
9 7
10 7
样例输出 #2
2
3 2
2 4
2 1
2 4
5 1
5 1
2 1
2 0
0 0
0 0
提示
【样例1说明】
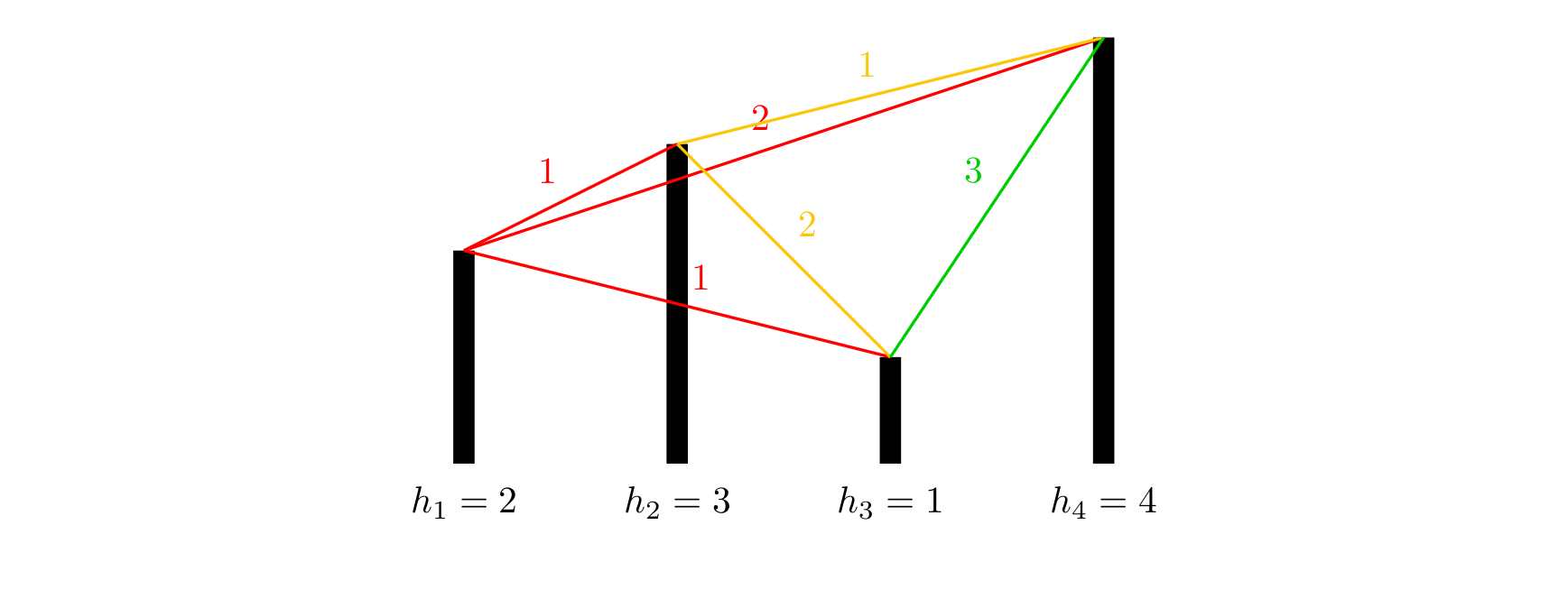
各个城市的海拔高度以及两个城市间的距离如上图所示。
如果从城市 1 1 1 出发,可以到达的城市为 2 , 3 , 4 2,3,4 2,3,4,这几个城市与城市 1 1 1 的距离分别为 1 , 1 , 2 1,1,2 1,1,2,但是由于城市 3 3 3 的海拔高度低于城市 2 2 2,所以我们认为城市 3 3 3 离城市 1 1 1 最近,城市 2 2 2 离城市 1 1 1 第二近,所以小A会走到城市 2 2 2。到达城市 2 2 2 后,前面可以到达的城市为 3 , 4 3,4 3,4,这两个城市与城市 2 2 2 的距离分别为 2 , 1 2,1 2,1,所以城市 4 4 4 离城市 2 2 2 最近,因此小B会走到城市 4 4 4。到达城市 4 4 4 后,前面已没有可到达的城市,所以旅行结束。
如果从城市 2 2 2 出发,可以到达的城市为 3 , 4 3,4 3,4,这两个城市与城市 2 2 2 的距离分别为 2 , 1 2,1 2,1,由于城市 3 3 3 离城市 2 2 2 第二近,所以小 A \text A A 会走到城市 3 3 3。到达城市 3 3 3 后,前面尚未旅行的城市为 4 4 4,所以城市 4 4 4 离城市 3 3 3 最近,但是如果要到达城市 4 4 4,则总路程为 2 + 3 = 5 > 3 2+3=5>3 2+3=5>3,所以小 B \text B B 会直接在城市 3 3 3 结束旅行。
如果从城市 3 3 3 出发,可以到达的城市为 4 4 4,由于没有离城市 3 3 3 第二近的城市,因此旅行还未开始就结束了。
如果从城市 4 4 4 出发,没有可以到达的城市,因此旅行还未开始就结束了。
【样例2说明】
当 x = 7 x=7 x=7 时,如果从城市 1 1 1 出发,则路线为 1 → 2 → 3 → 8 → 9 1 \to 2 \to 3 \to 8 \to 9 1→2→3→8→9,小 A \text A A 走的距离为 1 + 2 = 3 1+2=3 1+2=3,小 B \text B B 走的距离为 1 + 1 = 2 1+1=2 1+1=2。(在城市 1 1 1 时,距离小 A \text A A 最近的城市是 2 2 2 和 6 6 6,但是城市 2 2 2 的海拔更高,视为与城市 1 1 1 第二近的城市,所以小 A \text A A 最终选择城市 2 2 2;走到 9 9 9 后,小 A \text A A 只有城市 10 10 10 可以走,没有第二选择可以选,所以没法做出选择,结束旅行)
如果从城市 2 2 2 出发,则路线为 2 → 6 → 7 2 \to 6 \to 7 2→6→7,小 A \text A A 和小 B \text B B 走的距离分别为 2 , 4 2,4 2,4。
如果从城市 3 3 3 出发,则路线为 3 → 8 → 9 3 \to 8 \to 9 3→8→9,小 A \text A A 和小 B \text B B 走的距离分别为 2 , 1 2,1 2,1。
如果从城市 4 4 4 出发,则路线为 4 → 6 → 7 4 \to 6 \to 7 4→6→7,小 A \text A A 和小 B \text B B 走的距离分别为 2 , 4 2,4 2,4。
如果从城市 5 5 5 出发,则路线为 5 → 7 → 8 5 \to 7 \to 8 5→7→8,小 A \text A A 和小 B \text B B 走的距离分别为 5 , 1 5,1 5,1。
如果从城市 6 6 6 出发,则路线为 6 → 8 → 9 6 \to 8 \to 9 6→8→9,小 A \text A A 和小 B \text B B 走的距离分别为 5 , 1 5,1 5,1。
如果从城市 7 7 7 出发,则路线为 7 → 9 → 10 7 \to 9 \to 10 7→9→10,小 A \text A A 和小 B \text B B 走的距离分别为 2 , 1 2,1 2,1。
如果从城市 8 8 8 出发,则路线为 8 → 10 8 \to 10 8→10,小 A \text A A 和小 B \text B B 走的距离分别为 2 , 0 2,0 2,0。
如果从城市 9 9 9 出发,则路线为 9 9 9,小 A \text A A 和小 B \text B B 走的距离分别为 0 , 0 0,0 0,0(旅行一开始就结束了)。
如果从城市 10 10 10 出发,则路线为 10 10 10,小 A \text A A 和小 B \text B B 走的距离分别为 0 , 0 0,0 0,0。
从城市 2 2 2 或者城市 4 4 4 出发小 A \text A A 行驶的路程总数与小 B \text B B 行驶的路程总数的比值都最小,但是城市 2 2 2 的海拔更高,所以输出第一行为 2 2 2。
【数据范围与约定】
对于 30 % 30\% 30% 的数据,有 1 ≤ n ≤ 20 , 1 ≤ m ≤ 20 1\le n \le 20,1\le m\le 20 1≤n≤20,1≤m≤20;
对于 40 % 40\% 40% 的数据,有 1 ≤ n ≤ 100 , 1 ≤ m ≤ 100 1\le n \le 100,1\le m\le 100 1≤n≤100,1≤m≤100;
对于 50 % 50\% 50% 的数据,有 1 ≤ n ≤ 100 , 1 ≤ m ≤ 1000 1\le n \le 100,1\le m\le 1000 1≤n≤100,1≤m≤1000;
对于 70 % 70\% 70% 的数据,有 1 ≤ n ≤ 1000 , 1 ≤ m ≤ 1 0 4 1\le n \le 1000,1\le m\le 10^4 1≤n≤1000,1≤m≤104;
对于 100 % 100\% 100% 的数据: 1 ≤ n , m ≤ 1 0 5 1\le n,m \le 10^5 1≤n,m≤105, − 1 0 9 ≤ h i ≤ 1 0 9 -10^9 \le h_i≤10^9 −109≤hi≤109, 1 ≤ s i ≤ n 1 \le s_i \le n 1≤si≤n, 0 ≤ x i ≤ 1 0 9 0 \le x_i \le 10^9 0≤xi≤109
数据保证 h i h_i hi 互不相同。
算法思想
根据题目描述,本题要求的是选择一个城市 s s s 作为起点,一直向东行驶,并且最多行驶 x x x 公里就结束旅行时,小 A \text{A} A 开车行驶的路程总数以及小 B \text B B 行驶的路程总数。
由于小 A \text{A} A和小 B \text{B} B一直向东行驶,并且最多行驶 x x x 公里就结束旅行,可以使用倍增法统计出小 A \text{A} A 和小 B \text B B 开车行驶的路程总数 l a la la和 l b lb lb。
状态表示
- d a ( 0 , s , i ) da(0,s,i) da(0,s,i)表示从城市 s s s出发,小 A \text{A} A先走,两人轮流行驶了 2 i 2^i 2i次,小 A \text{A} A行驶的总距离。
- d a ( 1 , s , i ) da(1,s,i) da(1,s,i)表示从城市 s s s出发,小 B \text{B} B先走,两人轮流行驶了 2 i 2^i 2i次,小 A \text{A} A行驶的总距离。
- d b ( 0 , s , i ) db(0,s,i) db(0,s,i)表示从城市 s s s出发,小 A \text{A} A先走,两人轮流行驶了 2 i 2^i 2i次,小 B \text{B} B行驶的总距离。
- d b ( 1 , s , i ) db(1,s,i) db(1,s,i)表示从城市 s s s出发,小 B \text{B} B先走,两人轮流行驶了 2 i 2^i 2i次,小 B \text{B} B行驶的总距离。
有了上述状态,如何求从 s s s 出发,最多行驶 x x x 公里时的 l a la la和 l b lb lb呢?不妨设两人轮流行驶了 k k k次,以二进制的方式分析,假设 k = ( 011010010 ) 2 k=(011010010)_2 k=(011010010)2,那么
l a = d a ( 0 , s , 7 ) + d a ( 0 , s 1 , 6 ) + d a ( 0 , s 2 , 4 ) + d a ( 0 , s 3 , 1 ) l b = d b ( 0 , s , 7 ) + d b ( 0 , s 1 , 6 ) + d b ( 0 , s 2 , 4 ) + d b ( 0 , s 3 , 1 ) la = da(0,s,7)+da(0,s_1,6)+da(0,s_2,4)+da(0,s_3,1)\\ lb = db(0,s,7)+db(0,s_1,6)+db(0,s_2,4)+db(0,s_3,1) la=da(0,s,7)+da(0,s1,6)+da(0,s2,4)+da(0,s3,1)lb=db(0,s,7)+db(0,s1,6)+db(0,s2,4)+db(0,s3,1)
其中 s 1 , s 2 , s 3 . . . s_1,s_2,s_3... s1,s2,s3...为中间经过的城市。要求解中间经过的城市,还需要预处理
- f ( 0 , s , i ) f(0,s,i) f(0,s,i)表示从城市 s s s出发,小 A \text{A} A先走,两人轮流行驶了 2 i 2^i 2i次到达的城市编号
- f ( 1 , s , i ) f(1,s,i) f(1,s,i)表示从城市 s s s出发,小 B \text{B} B先走,两人轮流行驶了 2 i 2^i 2i次到达的城市编号
由于题目要求,小 A \text{A} A和小 B \text{B} B的驾驶风格不同。因此,还需要预处理出:
- g a ( i ) ga(i) ga(i)表示小 A \text{A} A从城市 s s s出发能够到达的城市编号
- g b ( i ) gb(i) gb(i)表示小 B \text{B} B从城市 s s s出发能够到达的城市编号
下面再来考虑一些如何计算上述状态
状态计算
1、 先来看一下如何计算 g a ga ga和 g b gb gb:
- 由于小 A \text{A} A总是沿着前进方向选择第二近的城市作为目的地,那么就是求城市 s s s右边和它的海拔高度之差第 2 2 2小的城市
- 小 B \text{B} B 总是沿着前进方向选择一个最近的城市作为目的地,那么就是求城市 s s s右边和它的海拔高度之差最小的城市
即在 s s s右侧的城市中,查找与 s s s高度之差的绝对值最小的两个城市,其原理类似于博主的这篇文章——邻值查找。
为了快速查找目标,可以使用set作为容器,从后向前遍历每个城市:
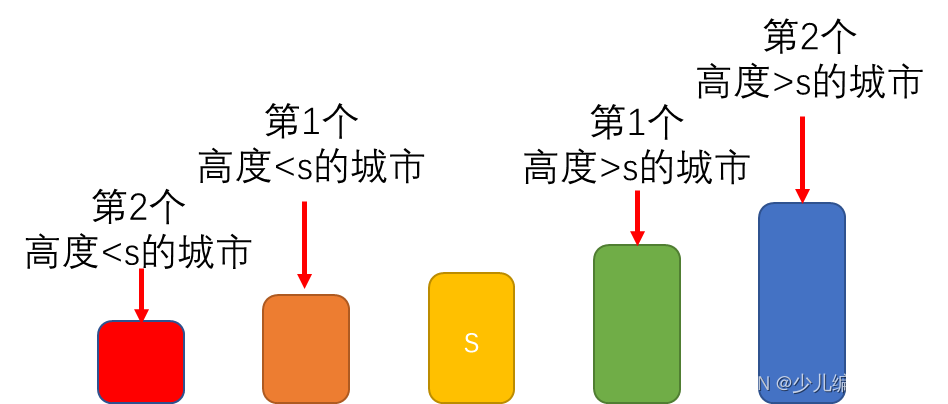
- 查找第 1 1 1个高度大于 h [ s ] h[s] h[s]的城市和第 2 2 2个高度大于 h [ s ] h[s] h[s]的城市
- 查找第 1 1 1个高度小于 h [ s ] h[s] h[s]的城市和第 2 2 2个高度小于 h [ s ] h[s] h[s]的城市
- 那么,目标就在这 4 4 4个城市之间,如下图所示。
- 再将城市 s s s插入到
set中。
2、再看如何计算 f ( 0 , s , i ) f(0,s,i) f(0,s,i)和 f ( 0 , s , i ) f(0,s,i) f(0,s,i)
- 当 i = 0 i=0 i=0时,表示从 s s s出发行驶 1 1 1次,那么 f ( 0 , s , 0 ) = g a ( s ) f(0,s,0) = ga(s) f(0,s,0)=ga(s), f ( 1 , s , 0 ) = g b ( s ) f(1,s,0) = gb(s) f(1,s,0)=gb(s),
- 当 i = 1 i=1 i=1时,表示从 s s s出发行驶 2 2 2次
- 第 1 1 1次小 A \text{A} A先驾驶从 s s s行驶到 f ( 0 , s , 0 ) f(0,s,0) f(0,s,0)
- 第 2 2 2次换小 B \text{B} B驾驶从 f ( 0 , s , 0 ) f(0,s,0) f(0,s,0)行驶到了 f ( 1 , f ( 0 , s , 0 ) , 0 ) f(1,f(0,s,0),0) f(1,f(0,s,0),0)
- k k k表示由谁先驾驶, k = 0 k=0 k=0表示小 A \text{A} A先驾驶, k = 1 k=1 k=1表示小 B \text{B} B先驾驶,那么 f ( k , s , 1 ) = f ( 1 − k , f ( k , s , 0 ) , 0 ) f(k,s,1)=f(1-k,f(k,s,0),0) f(k,s,1)=f(1−k,f(k,s,0),0)
- 当 i > 1 i>1 i>1时,表示从 s s s出发行驶 2 i 2^i 2i次,也可以分成两部分
- 第一部分, 小 A \text{A} A先驾驶从 s s s行驶到 f ( 0 , s , i − 1 ) f(0,s,i-1) f(0,s,i−1)
- 第二部分,由于 i > 1 i>1 i>1, 2 i − 1 2^{i-1} 2i−1是偶数,不换人,还有由小 A \text{A} A先驾驶从 f ( 0 , s , i − 1 ) f(0,s,i-1) f(0,s,i−1),行驶到 f ( 0 , f ( 0 , s , i − 1 ) , i − 1 ) f(0,f(0,s,i-1),i-1) f(0,f(0,s,i−1),i−1)
- 即 f ( k , s , i ) = f ( k , f ( k , s , i − 1 ) , i − 1 ) f(k,s,i)=f(k,f(k,s,i-1),i-1) f(k,s,i)=f(k,f(k,s,i−1),i−1)
3、最后再计算 d a da da和 d b db db
-
当 i = 0 i=0 i=0时,即行驶 1 1 1次
- d a ( 0 , s , 0 ) da(0,s,0) da(0,s,0)表示小 A \text{A} A先走,行驶 1 1 1次,会从城市 s s s到达 g a ( s ) ga(s) ga(s),那么 d a ( 0 , s , 0 ) = d i s t ( s , g a ( s ) ) da(0,s,0)=dist(s, ga(s)) da(0,s,0)=dist(s,ga(s)),即这两个城市海拔高度之差的绝对值;如果小 B \text{B} B先走,那么小 A \text{A} A行驶的距离为 0 0 0,即 d a ( 1 , s , 0 ) = 0 da(1,s,0)=0 da(1,s,0)=0
- 同理, d b ( 1 , s , 0 ) = d i s t ( s , g b ( s ) ) db(1,s,0)=dist(s, gb(s)) db(1,s,0)=dist(s,gb(s)), d b ( 0 , s , 0 ) = 0 db(0,s,0)=0 db(0,s,0)=0
-
当 i = 1 i=1 i=1时,即行驶 2 2 2次,可以分成两部分,不妨用 k k k表示谁先行驶, k = { 0 , 1 } k=\{0,1\} k={0,1}
- 第一部分从 s s s出发,行驶 1 1 1次,走到 f ( k , s , 0 ) f(k,s,0) f(k,s,0),小 A \text{A} A行驶的距离 d a ( k , s , 0 ) da(k,s,0) da(k,s,0),
小 B \text{B} B行驶的距离为 d b ( k , s , 0 ) db(k,s,0) db(k,s,0) - 第二部分从 f ( k , s , 0 ) f(k,s,0) f(k,s,0)出发,换人行驶 1 1 1次,小 A \text{A} A行驶的距离 d a ( 1 − k , f ( k , s , 0 ) , 0 ) da(1-k,f(k,s,0),0) da(1−k,f(k,s,0),0),
小 B \text{B} B行驶的距离为 d b ( k , f ( k , s , 0 ) , 0 ) db(k,f(k,s,0),0) db(k,f(k,s,0),0) - 那么, d a ( k , s , 1 ) = d a ( k , s , 0 ) + d a ( 1 − k , f ( k , s , 0 ) , 0 ) da(k,s,1)=da(k,s,0)+da(1-k,f(k,s,0),0) da(k,s,1)=da(k,s,0)+da(1−k,f(k,s,0),0), d b ( k , s , 1 ) = d b ( k , s , 0 ) + d b ( 1 − k , f ( k , s , 0 ) , 0 ) db(k,s,1)=db(k,s,0)+db(1-k,f(k,s,0),0) db(k,s,1)=db(k,s,0)+db(1−k,f(k,s,0),0)
- 第一部分从 s s s出发,行驶 1 1 1次,走到 f ( k , s , 0 ) f(k,s,0) f(k,s,0),小 A \text{A} A行驶的距离 d a ( k , s , 0 ) da(k,s,0) da(k,s,0),
-
当 i > 1 i>1 i>1时,即行驶 2 i 2^i 2i次,也可以分成两部分, k k k表示谁先行驶, k = { 0 , 1 } k=\{0,1\} k={0,1}
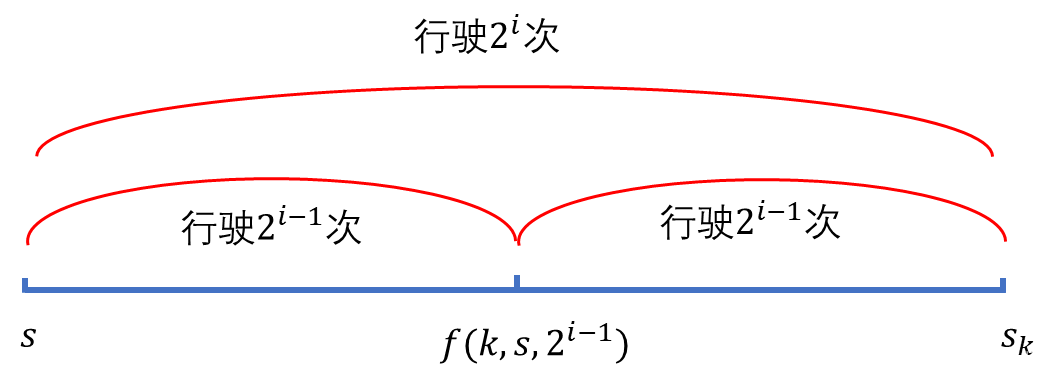
- d a ( k , s , i ) = d a ( k , s , i − 1 ) + d a ( k , f ( k , s , i − 1 ) , i − 1 ) da(k,s,i)=da(k,s,i-1)+da(k,f(k,s,i-1),i-1) da(k,s,i)=da(k,s,i−1)+da(k,f(k,s,i−1),i−1)
- d b ( k , s , i ) = d b ( k , s , i − 1 ) + d b ( 1 − k , f ( k , s , i − 1 ) , i − 1 ) db(k,s,i)=db(k,s,i-1)+db(1-k,f(k,s,i-1),i-1) db(k,s,i)=db(k,s,i−1)+db(1−k,f(k,s,i−1),i−1)
如下图所示
时间复杂度
- 预处理 g a , g b ga,gb ga,gb需要从后向前遍历每个城市 s s s,查找与 s s s高度之差的绝对值最小的两个城市,使用
set容器查找的时间复杂度为 O ( l o g n ) O(logn) O(logn),总的时间复杂度为 O ( n l o g n ) O(nlogn) O(nlogn) - 通过倍增法预处理 f f f的时间复杂度为 O ( n l o g n ) O(nlogn) O(nlogn)
- 通过倍增法预处理 d a , d b da,db da,db的时间复杂度为 O ( n l o g n ) O(nlogn) O(nlogn)
- 第一问求对于给定的 x x x,从哪个城市出发,小 A \text A A 开车行驶的路程总数与小 B \text B B 行驶的路程总数的比值最小,需要枚举每个城市作为起点,求 l a la la和 l b lb lb,时间复杂度为 O ( n l o g n ) O(nlogn) O(nlogn)
- 第二问一共有 m m m个询问,求在给定的 s s s 和 x x x 情况下求小 A \text A A 行驶的里程总数和小 B \text B B 行驶的里程总数,时间复杂度为 O ( m l o g n ) O(mlogn) O(mlogn)
总的时间复杂度为 O ( n l o g n ) = 1 0 5 × 17 O(nlogn)=10^5\times17 O(nlogn)=105×17
代码实现
#include <iostream>
#include <set>
using namespace std;
typedef long long LL;
typedef pair<LL, int> PLI;
const int N = 1e5 + 10, M = 17;
const LL INF = 1e18;
int n, h[N];
int ga[N], gb[N]; //ga[i]表示小A从i出发能到达的城市
int f[2][N][M]; //f[0][s][i]表示从s出发,小A先走,轮流行驶2^i时到达的城市编号
int da[2][N][M], db[2][N][M];
void init_g()
{set<PLI> S;//防止查找越界,插入4个边界S.insert({-INF, 0}), S.insert({-INF + 1, 0});S.insert({INF, 0}), S.insert({INF + 1, 0});PLI b[4]; //被选城市//从后向前遍历城市,查找右侧第一个大于h[i]的位置for(int i = n; i >= 0; i --){PLI t(h[i], i);auto it = S.upper_bound(t);it ++; //移动到右侧第二个大于h[i]的位置for(int k = 0; k < 4; k ++) b[k] = *it --;//从备选的4个备选城市中查找差值第1小和第2小的城市LL d1 = INF, d2 = INF;int p1, p2;for(int k = 3; k >= 0; k --){LL d = abs(h[i] - b[k].first);if(d < d1) {d2 = d1, d1 = d;p2 = p1, p1 = b[k].second; }else if(d < d2) {d2 = d, p2 = b[k].second;}}//小A选择第二近的城市作为目的地,小B选择一个最近的城市作为目的地,ga[i] = p2, gb[i] = p1;S.insert(t);}
}
void init_f()
{//初始状态,从每个城市出发行驶1次能到达的城市for(int s = 1; s <= n; s ++) {f[0][s][0] = ga[s], f[1][s][0] = gb[s];}//状态计算for(int i = 1; i < M; i ++)for(int s = 1; s <= n; s ++)for(int k = 0; k < 2; k ++){if(i == 1) //行驶2次f[k][s][i] = f[1 - k][f[k][s][0]][0];else //行驶2^if[k][s][i] = f[k][f[k][s][i - 1]][i - 1];}
}
//获取两个城市之间的距离
int get_dis(int a, int b)
{return abs(h[a] - h[b]);
}
void init_d()
{//初始状态,计算从每个城市出发行驶1次能够走的额距离for(int s = 1; s <= n; s ++){da[0][s][0] = get_dis(s, ga[s]);db[1][s][0] = get_dis(s, gb[s]);}//状态计算for(int i = 1; i < M; i ++)for(int s = 1; s <= n; s ++)for(int k = 0; k < 2; k ++){if(i == 1) //行驶2次{da[k][s][i] = da[k][s][i - 1] + da[1 - k][f[k][s][i - 1]][i - 1];db[k][s][i] = db[k][s][i - 1] + db[1 - k][f[k][s][i - 1]][i - 1];}else //行驶2^i次{da[k][s][i] = da[k][s][i - 1] + da[k][f[k][s][i - 1]][i - 1];db[k][s][i] = db[k][s][i - 1] + db[k][f[k][s][i - 1]][i - 1];}}
}
//计算从城市s出发,行驶总距离不超过s时,小A和小B各自走的总距离
void work(int s, int x, int &la, int &lb)
{la = lb = 0;//枚举行驶次数for(int i = M - 1; i >= 0; i --){//如果能够到达城市,并且总距离不超过xif(f[0][s][i] && la + lb + da[0][s][i] + db[0][s][i] <= x){la += da[0][s][i], lb += db[0][s][i];s = f[0][s][i];//行驶到新的城市s}}
}
int main()
{scanf("%d", &n);for(int i = 1; i <= n; i ++) scanf("%d", &h[i]);//预处理状态init_g();init_f();init_d();//第一问int x;scanf("%d", &x);int ans = 0, max_h = 0;double min_r = INF;for(int s = 1; s <= n; s ++){int la, lb;work(s, x, la, lb);double r = lb == 0 ? INF : (double) la / lb;//取最小比值,比值相同取海拔更高的城市if(r < min_r || r == min_r && h[s] > max_h){min_r = r, max_h = h[s], ans = s;}}printf("%d\n", ans);//第二问int m;scanf("%d", &m);while (m -- ){int s, x, la, lb;scanf("%d%d", &s, &x);work(s, x, la, lb);printf("%d %d\n", la, lb);}return 0;
}相关文章:

NOIP2012提高组day1-T3:开车旅行
题目链接 [NOIP2012 提高组] 开车旅行 题目描述 小 A \text{A} A 和小 B \text{B} B 决定利用假期外出旅行,他们将想去的城市从 1 1 1 到 n n n 编号,且编号较小的城市在编号较大的城市的西边,已知各个城市的海拔高度互不相同…...

Golang Web框架性能对比
Golang Web框架性能对比 github star排名依次: Gin Beego Iris Echo Revel Buffalo 性能上gin、iris、echo网上是给的数据都是五星,beego三星,revel两星 beego是国产,有中文文档,文档齐全 根据star数,性能,易用程度…...

【OCR】 - Tesseract OCR在mac系统中安装
Tesseract OCR 在Mac环境下安装Tesseract OCR(Optical Character Recognition)通常可以通过Homebrew包管理器进行。以下是安装步骤: 安装Homebrew 如果你还没有安装Homebrew,请访问 https://brew.sh/ 并按照页面上的说明安装。…...
了解不同方式导入导出的速度之快
目录 一、用工具导出导入 Navicat(速度慢) 1.1、导入: 共耗时: 1.2、导出表 共耗时: 二、用命令语句导出导入 2.1、mysqldump速度快 导出表数据和表结构 共耗时: 只导出表结构 导入 共耗时&…...

2024年第九届计算机与通信系统国际会议(ICCCS2024) ,邀您相约西安!
会议官网: ICCCS2024 | Xian China 时间: 2024年4月19-22日 地点: 中国西安 会议简介: 近年来,信息通信在不断发展,为计算机网络的进步与发展提供了先进可靠的技术支持。随着计算机网络与通信技术的深入发展,计算机通信技术、数…...

获取直播间的最新评论 - python 取两个list的差集
python 取两个list的差集 作用:比如我要获取评论区列表,先获取了一遍,这个时候有人评论了几条,我再获取一遍后,找出多的那几条 使用set数据类型来取两个列表的差集。差集表示仅包含在第一个列表中而不在第二个列表中…...

2023年度总结:但行前路,不负韶华
🦁作者简介:一名喜欢分享和记录学习的在校大学生 🐯个人主页:妄北y 🐧个人QQ:2061314755 🐻个人邮箱:2061314755qq.com 🦉个人WeChat:Vir2021GKBS &#x…...

智数融合|低代码入局,推动工业数字化转型走"深"向"实"
当下,“数字化、智能化”已经不再是新鲜词汇。事实上,早在几年前,就有企业开始大力推动数字化转型,并持续进行了一段时间。一些业内人士甚至认为,“如今的企业数字化已经走过了成熟期,进入了深水区。” 但事…...

初学者的基本 Python 面试问题和答案
文章目录 专栏导读1、什么是Python?列出 Python 在技术领域的一些流行应用。2、在目前场景下使用Python语言作为工具有什么好处?3、Python是编译型语言还是解释型语言?4、Python 中的“#”符号有什么作用?5、可变数据类型和不可变…...
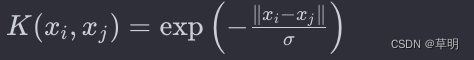
支持向量机(Support Vector Machines,SVM)
什么是机器学习 支持向量机(Support Vector Machines,SVM)是一种强大的机器学习算法,可用于解决分类和回归问题。SVM的目标是找到一个最优的超平面,以在特征空间中有效地划分不同类别的样本。 基本原理 超平面 在二…...

golang一个轻量级基于内存的kv存储或缓存
golang一个轻量级基于内存的kv存储或缓存 go-cache是一个轻量级的基于内存的key:value 储存组件,类似于memcached,适用于在单机上运行的应用程序。 它的主要优点是,本质上是一个具有过期时间的线程安全map[string]interface{}。interface的结…...

henauOJ 1103: 统计元音
题目描述 统计每个元音字母在字符串中出现的次数。 输入 输入数据首先包括一个整数n,表示测试实例的个数,然后是n行长度不超过100的字符串。 输出 对于每个测试实例输出5行,格式如下: a:num1 e:num2 i:num3 o:num4 u:num5 多…...

虚幻引擎:开创视觉与创意的新纪元
先看看据说虚幻5做出来的东西吧: 虚幻引擎5!!!4K画质PS5实机演示! 好了,用文字认识一下吧: 虚幻引擎5.3对UE5的核心工具集作了进一步优化,涉及渲染、世界构建、程序化内容生成&…...
T527 Android 13 编译步骤
步骤1: cd longan./build.sh config (0 2 1) 选择 Android 平台: 步骤2:选择IC为t527: 步骤3:板子类型选为demo_car: 步骤4:选择 flash,默认选择 default 则可: 步骤5&…...

OpenAI ChatGPT-4开发笔记2024-04:Chat之Tool之2:multiple functions
从程序员到ai Expert 1 定义参数和函数2 第一轮chatgpt3 第一轮结果和function定义全部加入prompt再喂给chatgpt4 大结局7 参考资料 上一篇解决了调用一个函数的问题。这一篇扩展为调用3个。n个自行脑补。 1 定义参数和函数 #1.设定目标 import json import openai#1.定义para…...
14:00面试,14:07就出来了,问的问题有点变态。。。
前言 刚从小厂出来,没想到网盘我在另一家公司又寄了。 在这家公司上班,每天都要加班,但看在钱给的比较多的份上,也就不太计较了。但万万没想到一纸通知,所有人不准加班了,不仅加班费没有了,薪…...
206. 反转链表(Java)
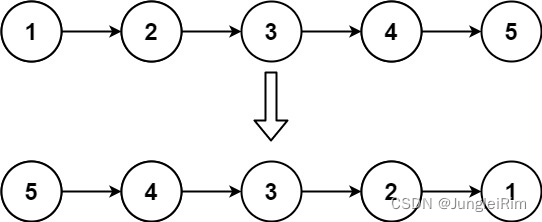
题目描述: 给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。 输入: head [1,2,3,4,5] 输出: [5,4,3,2,1] 代码实现: 1.根据题意创建一个结点类: public class ListNode {int val…...
LeetCode 2807. 在链表中插入最大公约数【链表,迭代,递归】1279
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

Hive之set参数大全-3
D 是否启用本地任务调试模式 hive.debug.localtask 是 Apache Hive 中的一个配置参数,用于控制是否启用本地任务调试模式。在调试模式下,Hive 将尝试在本地模式下运行一些任务,以便更容易调试和分析问题。 具体来说,当 hive.de…...
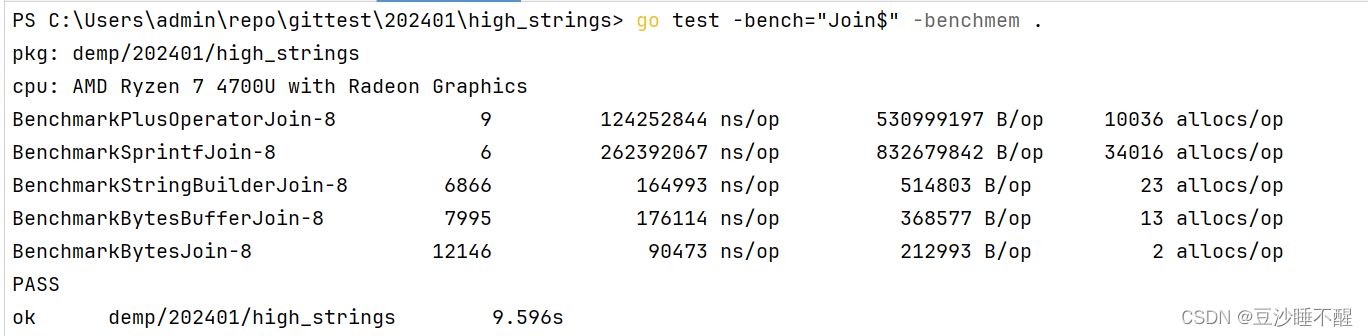
Golang拼接字符串性能对比
g o l a n g golang golang的 s t r i n g string string类型是不可修改的,对于拼接字符串来说,本质上还是创建一个新的对象将数据放进去。主要有以下几种拼接方式 拼接方式介绍 1.使用 s t r i n g string string自带的运算符 ans ans s2. 使用…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...

归并排序:分治思想的高效排序
目录 基本原理 流程图解 实现方法 递归实现 非递归实现 演示过程 时间复杂度 基本原理 归并排序(Merge Sort)是一种基于分治思想的排序算法,由约翰冯诺伊曼在1945年提出。其核心思想包括: 分割(Divide):将待排序数组递归地分成两个子…...
