加工零件的题解
目录
原题描述:
题目描述
输入格式
输出格式
样例 #1
样例输入 #1
样例输出 #1
样例 #2
样例输入 #2
样例输出 #2
提示
题目大意:
主要思路:
但是我们怎么才能判断出x走到1时L是偶数还是奇数呢?
初始化:
代码code:
原题描述:
时间限制: 1000ms
空间限制: 524288kB
题目描述
凯凯的工厂正在有条不紊地生产一种神奇的零件,神奇的零件的生产过程自然也很神奇。工厂里有 位工人,工人们从
编号。某些工人之间存在双向的零件传送带。保证每两名工人之间最多只存在一条传送带。
如果 号工人想生产一个被加工到第
阶段的零件,则所有与
号工人有传送带直接相连的工人,都需要生产一个被加工到第
阶段的零件(但
号工人自己无需生产第
阶段的零件)。
如果 号工人想生产一个被加工到第 1 阶段的零件,则所有与
号工人有传送带直接相连的工人,都需要为
号工人提供一个原材料。
轩轩是 1 号工人。现在给出 张工单,第
张工单表示编号为
的工人想生产一个第
阶段的零件。轩轩想知道对于每张工单,他是否需要给别人提供原材料。他知道聪明的你一定可以帮他计算出来!
输入格式
第一行三个正整数,分别表示工人的数目、传送带的数目和工单的数目。
接下来 行,每行两个正整数
和
,表示编号为
和
的工人之间存在一条零件传输带。保证
。
接下来 行,每行两个正整数
和
,表示编号为
的工人想生产一个第
阶段的零件。
输出格式
共 行,每行一个字符串
Yes 或者 No。如果按照第张工单生产,需要编号为 1 的轩轩提供原材料,则在第
行输出
Yes;否则在第 行输出
No。注意输出不含引号。
样例 #1
样例输入 #1
3 2 6
1 2
2 3
1 1
2 1
3 1
1 2
2 2
3 2样例输出 #1
No
Yes
No
Yes
No
Yes样例 #2
样例输入 #2
5 5 5
1 2
2 3
3 4
4 5
1 5
1 1
1 2
1 3
1 4
1 5样例输出 #2
No
Yes
No
Yes
Yes提示
【输入输出样例 1 说明】
编号为 1 的工人想生产第 1 阶段的零件,需要编号为 2 的工人提供原材料。
编号为 2 的工人想生产第 1 阶段的零件,需要编号为 1 和 3 的工人提供原材料。
编号为 3 的工人想生产第 1 阶段的零件,需要编号为 2 的工人提供原材料。
编号为 1 的工人想生产第 2 阶段的零件,需要编号为 2 的工人生产第 1 阶段的零 件,需要编号为 1 和 3 的工人提供原材料。
编号为 2 的工人想生产第 2 阶段的零件,需要编号为 1 和 3 的工人生产第 1 阶段的零件,他/她们都需要编号为 2 的工人提供原材料。
编号为 3 的工人想生产第 2 阶段的零件,需要编号为 2 的工人生产第 1 阶段的零件,需要编号为 1 和 3 的工人提供原材料。
【输入输出样例 2 说明】
编号为 1 的工人想生产第 1 阶段的零件,需要编号为 2 和 5 的工人提供原材料。
编号为 1 的工人想生产第 2 阶段的零件,需要编号为 2 和 5 的工人生产第 1 阶段的零件,需要编号为 的工人提供原材料。
编号为 1 的工人想生产第 3 阶段的零件,需要编号为 2 和 5 的工人生产第 2 阶段的零件,需要编号为的工人生产第 1 阶段的零件,需要编号为
的工人提供原材料。
编号为 1 的工人想生产第 4 阶段的零件,需要编号为 2 和 5 的工人生产第 3 阶段的零件,需要编号为 的工人生产第 2 阶段的零件,需要编号为
的工人生产第 1 阶段的零件,需要全部工人提供原材料。
编号为 1 的工人想生产第 5 阶段的零件,需要编号为 2 和 5 的工人生产第 4 阶段的零件,需要编号为 的工人生产第 3 阶段的零件,需要编号为
的工人生产第 2 阶段的零件,需要全部工人生产第 1 阶段的零件,需要全部工人提供原材料。
【数据规模与约定】
共 20 个测试点。
。
测试点 1~4,。
测试点 5~8,。
测试点 9~12,。
测试点 13~16,。
测试点 17~20,。
题目大意:
有一张无向图,每次有个节点a要级别为L的部件,则与a直接相连的节点要提供L-1的部件。
当节点a要1级的部件时,那么与a直接相连的节点要提供1个原材料。
问你每次节点1是否提供原材料。
主要思路:
这个题目可以用分类讨论。
分三个部分:(用cnt表示从节点a到1的路径长度(每条边长为1)
- L = cnt
- L<cnt
- L>cnt
对于部分1:
画图来看一下。

当L=cnt时,节点1要提供原材料。
注意:有些童鞋会说:4生产3,那么5又要生产2,不是还要进一步的推导吗?
可是题目中只说是否要1提供原材料,其他的就不用管太多。
第二部分:
L<cnt
还是画图:

我们发现,还没轮到1时,就结束了,说明1不用提供什么。
第三部分:
L>cnt
从x走到1时L是奇数。
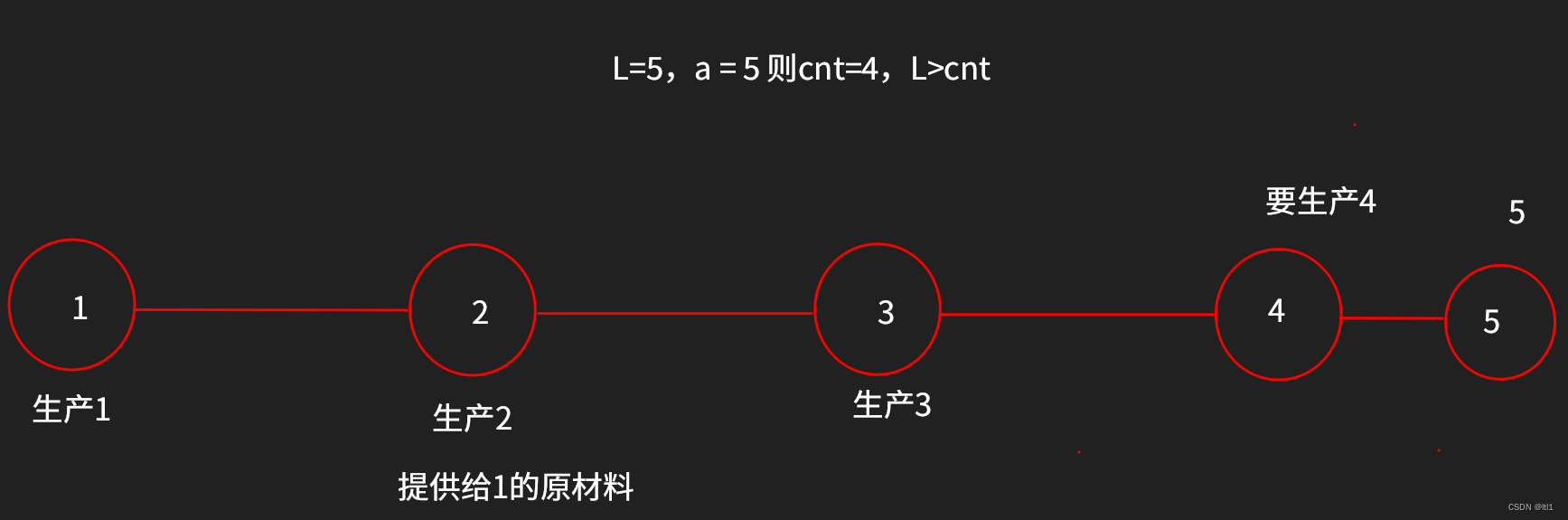
1不用提供任何原材料
但是but,当L>cnt 且从x走到1时L是偶数。
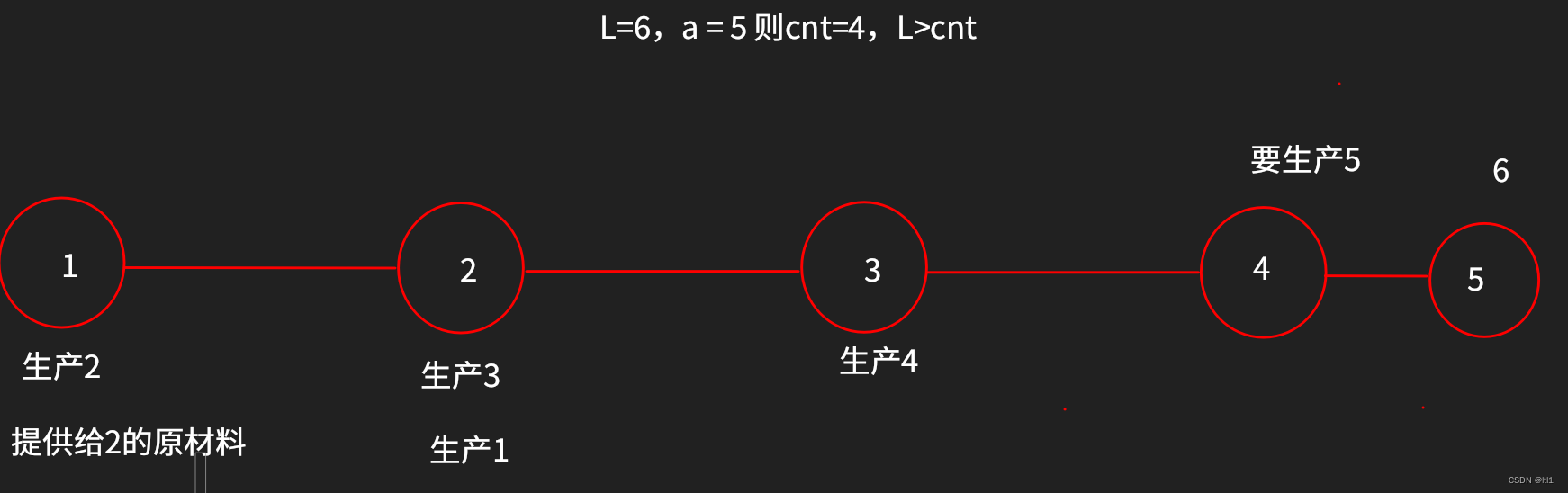
这时,1要提供原材料了。
得出结论:
当L = cnt,1要提供原材料。
当L < cnt,1不用提供任何原材料。
当L > cnt,且从x走到1时L-cnt是奇数,1不用提供任何原材料。
当L > cnt,且从x走到1时L是偶数,1要提供原材料。
但是我们怎么才能判断出x走到1时L是偶数还是奇数呢?
int even[100010];// even[x]表示:从1走到x,长度最短为偶数的路径的长度(even是偶数的意思)
int odd[100010];// odd[x]表示:从1走到x,长度最短为奇数的路径的长度(odd是奇数的意思)注:是最短路径。
奇数-奇数=偶数。
奇数-偶数=奇数
偶数-奇数=奇数
偶数-偶数=偶数。
cnt被替代了
这样我们就发现了:
L是奇数,且l>=odd[x](odd[x]肯定是奇数长度路径)那么就输出"Yes"(等于也输出Yes)
L是奇数,且l<odd[x](odd[x]肯定是奇数长度路径)那么就输出"No"
L是偶数,且l>=even[x](even[x]肯定是偶数长度路径)那么就输出"Yes"(等于也输出Yes)
L是偶数,且l<even[x](even[x]肯定是偶数长度路径)那么就输出"No"
不明白为啥就看重新看一下三个部分。
初始化:
都初始化成0x3f(是一个较大数就可以了)
代码code:
#include<bits/stdc++.h>
using namespace std;
int n,m,q;
int even[100010];// even[x]表示:从1走到x,长度最短为偶数的路径的长度(even是偶数的意思)
int odd[100010];// odd[x]表示:从1走到x,长度最短为奇数的路径的长度(odd是奇数的意思)
vector<vector<int>> v(100010);
//int vis[100010][10010];
void init()
{queue<pair<int,int>> q;q.push({1,0});while(!q.empty()){int node=q.front().first,step=q.front().second;q.pop();for(auto it:v[node]){if(step%2 == 1&&even[it] == 0x3f3f3f3f){even[it] = step+1;
// vis[it][step+1] = 1;q.push({it,step+1});}if(step%2 == 0&&odd[it] == 0x3f3f3f3f)//有没有走过{odd[it] = step+1;
// vis[it][step+1] = 1;q.push({it,step+1});}/*有些童鞋会说,这里odd是奇数,可是为啥是放在step%2 == 0,里面不应该是放even吗。回答:step还要+1,因为已经走了这一步,要加一,偶数加1就是奇数,所以是odd放在里面。18行~23行同理*/}}
}
int main()
{cin>>n>>m>>q;for(int i=1;i<=m;i++){int u,v1;cin>>u>>v1;v[u].push_back(v1);v[v1].push_back(u);}memset(odd,0x3f,sizeof(odd));memset(even,0x3f,sizeof(even));init();while(q--){int l,x;cin>>x>>l;if(l%2 == 1){if(l>=odd[x]){cout<<"Yes\n";}else{cout<<"No\n";}}else{if(l>=even[x]){cout<<"Yes\n";}else{cout<<"No\n";}}}return 0;
}相关文章:

加工零件的题解
目录 原题描述: 题目描述 输入格式 输出格式 样例 #1 样例输入 #1 样例输出 #1 样例 #2 样例输入 #2 样例输出 #2 提示 题目大意: 主要思路: 但是我们怎么才能判断出x走到1时L是偶数还是奇数呢? 初始化:…...
走进shell
Linux系统启动时,会自动创建多个虚拟控制台。虚拟控制台是运行在Linux系统内存中的终端会话。 打开Linux控制台Terminal使用tty命令查看当前使用的虚拟控制台。 注:tty 表示电传打字机(teletypewriter) $ tty /dev/pts/0表示当前使用的是/dev/pts/0 虚拟…...
【Python】使用tkinter设计开发Windows桌面程序记事本(2)
上一篇:【Python】使用tkinter设计开发Windows桌面程序记事本(1)-CSDN博客 下一篇: 作者发炎 此代码模块是继承上一篇文章的代码模块的基础上开始设计开发的。 如果不知道怎么新建"记事本项目"文件夹,请参…...
Flutter DateTime 常用处理
今天介绍一下 DateTime 的一些常用功能,对其进行一个整理。 最近在开发过程中好多时候都会使用到时间方面的方法,心想还是统一处理一下,封装一个管理类,这个类可以满足我们开发过程中常用的时间方法。 今天正好整理了一下&#…...

【uniapp】APP打包上架应用商-注意事项
初雪云-uniapp启动图自定义生成(支持一键生成storyboard) HBuilderX需要的自定义storyboard文件格式为 " zip压缩包 " 一、“Android” — 设置targetSdkVersion 小米、OPPO、vivo、华为等主流应用商店,将于2023年12月采用 targetS…...

【算法题】43. 字符串相乘
题目 给定两个以字符串形式表示的非负整数 num1 和 num2,返回 num1 和 num2 的乘积,它们的乘积也表示为字符串形式。 注意:不能使用任何内置的 BigInteger 库或直接将输入转换为整数。 示例 1: 输入: num1 "2", num2 "3…...
CH341 SPI方式烧录BK7231U
CH341是一个USB总线的转接芯片,通过USB总线提供异步串口、打印口、并口以及常用的2线和4线等同步串行接口。 BK7231U Wi-Fi SOC芯片,内嵌处理器。1. 符合802.11b/g/n 1x1协议 2. 17dBm 输出功率3. 支持20/40 MHz带宽和STBC 4. 支持Wi-Fi STA、AP、…...

sd-webui-EasyPhoto win 安装笔记
目录 安装教程: 插件介绍 ControlNet 1.1 Tile: launch.py问题 依赖库 webui安装问题...

gradient_checkpointing
点评:本质是减少内存消耗的一种方式,以时间或者计算换内存 gradient_checkpointing(梯度检查点)是一种用于减少深度学习模型中内存消耗的技术。在训练深度神经网络时,反向传播算法需要在前向传播和反向传播之间存储中间计算结果,以便计算梯度并更新模型参数。这些中间结…...

回溯算法part05 算法
回溯算法part05 算法 今日任务 491.递增子序列46.全排列47.全排列 II 1.LeetCode 491.递增子序列 https://leetcode.cn/problems/non-decreasing-subsequences/description/ class Solution {List<List<Integer>> resultnew ArrayList<>();List<Inte…...

阿里云系统盘测评ESSD、SSD和高效云盘IOPS、吞吐量性能参数表
阿里云服务器系统盘或数据盘支持多种云盘类型,如高效云盘、ESSD Entry云盘、SSD云盘、ESSD云盘、ESSD PL-X云盘及ESSD AutoPL云盘等,阿里云百科aliyunbaike.com详细介绍不同云盘说明及单盘容量、最大/最小IOPS、最大/最小吞吐量、单路随机写平均时延等性…...
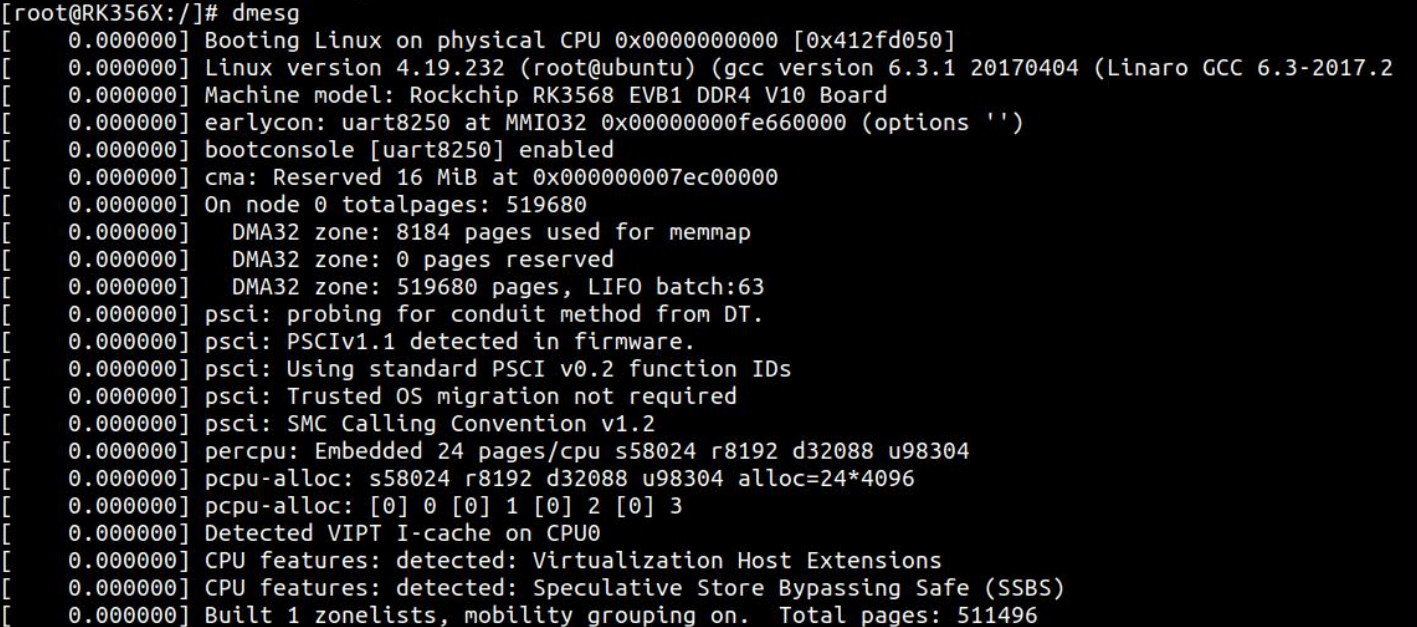
RK3568平台开发系列讲解(Linux系统篇)Linux 内核打印
🚀返回总目录 文章目录 一、方法一:dmseg 命令二、方法二:查看 kmsg 文件三、方法三:调整内核打印等级一、方法一:dmseg 命令 在终端使用 dmseg 命令可以获取内核打印信息,该命令的具体使用方法如下所示: 首先在串口终端使用 “dmseg”命令,可以看见相应的内核打印信息…...

迁移学习的最新进展和挑战
随着深度学习和人工智能技术的飞速发展,迁移学习作为一种有效的机器学习方法,已经在各个领域取得了显著的成果。迁移学习是指将一个领域(源领域)的知识应用到另一个领域(目标领域),以提高目标领…...

Python基础(二十二、自定义模块和包)
文章目录 一、自定义模块1.如何自定义模块并导入?2.__main__变量的功能3.注意事项 二、自定义包1.什么是Python的包?2.__init __.py文件的作用?3.__all__变量的作用?4.示例 三、自定义模块和自定义包的好处 一、自定义模块 1.如何自定义模块并导入? 在Python代码文件中正…...

C#-数组
数组 (array) 是一种包含若干变量的数据结构,这些变量都可以通过计算索引进行访问。数组中包含的变量(又称数组的元素)具有相同的类型,该类型称为数组的元素类型。 数组类型为引用类型,因此数组变量的声明只是为数组实…...

机器学习周刊第二期:300个机器学习应用案例集
大家好 前文:机器学习项目精选 第一期 继续分享我最近看过并觉得非常硬核的资源,包括Python、机器学习、深度学习、大模型等等。 1、Python编程挑战 地址:https://github.com/Asabeneh/30-Days-Of-Python 30天Python编程挑战是一个逐步学…...

【华为OD机试真题2023CD卷 JAVAJS】中文分词模拟器
华为OD2023(C&D卷)机试题库全覆盖,刷题指南点这里 中文分词模拟器 知识点图字符串 时间限制:5s 空间限制:256MB 限定语言:不限 题目描述: 给定一个连续不包含空格字符串,该字符串仅包含英文小写字母及英文文标点符号(逗号、分号、句号),同时给定词库,对该字符串进…...
检测)
基于YOLOv8-pose的画笔关键点(bic_markers)检测
💡💡💡本文解决什么问题:教会你如何用自己的数据集训练Yolov8-pose关键点检测 Yolov8-Pose关键点检测专栏介绍:https://blog.csdn.net/m0_63774211/category_12398833.html ✨✨✨手把手教你从数据标记到生成适合Yolov8-pose的yolo数据集;...

【实用技巧】Windows 电脑向iPhone或iPad传输视频方法1:无线传输
一、内容简介 本文介绍如何使用 Windows 电脑向 iPhone 或 iPad 传输视频,以 iPhone 为例,iPad的操作方法类似,本文不作赘述。 二、所需原材料 Windows 电脑(桌面或其它文件夹中存有要导入的视频)、iPhone 14。 待…...

爬虫实战 - 微博评论数据可视化
简介: 我们都知道在数据比较少的情况下,我们是可以很轻易的获取到数据中的信息。但是当数据比较庞大的时候呢,我们就很难看出来了。尤其是面对现如今数以万计的数据,就更了。 不过好在我们可以通过计算机来帮我们进行分析&#…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...

【HarmonyOS 5】鸿蒙中Stage模型与FA模型详解
一、前言 在HarmonyOS 5的应用开发模型中,featureAbility是旧版FA模型(Feature Ability)的用法,Stage模型已采用全新的应用架构,推荐使用组件化的上下文获取方式,而非依赖featureAbility。 FA大概是API7之…...

Canal环境搭建并实现和ES数据同步
作者:田超凡 日期:2025年6月7日 Canal安装,启动端口11111、8082: 安装canal-deployer服务端: https://github.com/alibaba/canal/releases/1.1.7/canal.deployer-1.1.7.tar.gz cd /opt/homebrew/etc mkdir canal…...

CppCon 2015 学习:Reactive Stream Processing in Industrial IoT using DDS and Rx
“Reactive Stream Processing in Industrial IoT using DDS and Rx” 是指在工业物联网(IIoT)场景中,结合 DDS(Data Distribution Service) 和 Rx(Reactive Extensions) 技术,实现 …...

Java多线程实现之Runnable接口深度解析
Java多线程实现之Runnable接口深度解析 一、Runnable接口概述1.1 接口定义1.2 与Thread类的关系1.3 使用Runnable接口的优势 二、Runnable接口的基本实现方式2.1 传统方式实现Runnable接口2.2 使用匿名内部类实现Runnable接口2.3 使用Lambda表达式实现Runnable接口 三、Runnabl…...
