剑指 Offer II 012. 左右两边子数组的和相等
题目链接
剑指 Offer II 012. 左右两边子数组的和相等 easy
题目描述
给你一个整数数组 nums,请计算数组的 中心下标 。
数组 中心下标 是数组的一个下标,其左侧所有元素相加的和等于右侧所有元素相加的和。
如果中心下标位于数组最左端,那么左侧数之和视为 0,因为在下标的左侧不存在元素。这一点对于中心下标位于数组最右端同样适用。
如果数组有多个中心下标,应该返回 最靠近左边 的那一个。如果数组不存在中心下标,返回 -1。
示例 1:
输入:nums = [1,7,3,6,5,6]
输出:3
解释:
中心下标是 3 。
左侧数之和 sum = nums[0] + nums[1] + nums[2] = 1 + 7 + 3 = 11 ,
右侧数之和 sum = nums[4] + nums[5] = 5 + 6 = 11 ,二者相等。
示例 2:
输入:nums = [1, 2, 3]
输出:-1
解释:
数组中不存在满足此条件的中心下标。
示例 3:
输入:nums = [2, 1, -1]
输出:0
解释:
中心下标是 0 。
左侧数之和 sum = 0 ,(下标 0 左侧不存在元素),
右侧数之和 sum = nums[1] + nums[2] = 1 + -1 = 0 。
提示:
- 1<=nums.length<=1041 <= nums.length <= 10^41<=nums.length<=104
- −1000<=nums[i]<=1000-1000 <= nums[i] <= 1000−1000<=nums[i]<=1000
分析:
对于原数组 nums[0 , n-1]区间,我们用前缀和数组 s[0 , n]来表示其前缀和,即:
- s[0]=0s[0] = 0s[0]=0
- s[1]=nums[0]s[1] = nums[0]s[1]=nums[0]
- s[2]=nums[0]+nums[1]s[2] = nums[0] + nums[1]s[2]=nums[0]+nums[1]
- s[3]=nums[0]+nums[1]+nums[2]s[3] = nums[0] + nums[1] + nums[2]s[3]=nums[0]+nums[1]+nums[2]
- …
那么对于 下标i,我们就能快速的得出它两边的和 leftsum = s[i-1],rightsum = s[n] - s[i]。我们只需要判断这两部分是否相等即可。
时间复杂度: O(n)O(n)O(n)
C++代码:
class Solution {
public:int pivotIndex(vector<int>& nums) {int n = nums.size();vector<int> s(n+1);for(int i = 1;i <= n;i++) s[i] = s[i-1] + nums[i-1];for(int i = 1;i <= n;i++){if(s[i-1] == s[n] - s[i]) return i - 1;}return -1;}
};
Java代码:
class Solution {public int pivotIndex(int[] nums) {int n = nums.length;int[] s = new int[n+1];for(int i = 1;i <= n;i++) s[i] = s[i-1] + nums[i-1];for(int i = 1;i <= n;i++){if(s[i-1] == s[n] - s[i]) return i - 1;}return -1;}
}相关文章:

剑指 Offer II 012. 左右两边子数组的和相等
题目链接 剑指 Offer II 012. 左右两边子数组的和相等 easy 题目描述 给你一个整数数组 nums,请计算数组的 中心下标 。 数组 中心下标 是数组的一个下标,其左侧所有元素相加的和等于右侧所有元素相加的和。 如果中心下标位于数组最左端,那…...

Java货物摆放
题目描述 小蓝有一个超大的仓库,可以摆放很多货物。 现在,小蓝有 � n 箱货物要摆放在仓库,每箱货物都是规则的正方体。小蓝规定了长、宽、高三个互相垂直的方向,每箱货物的边都必须严格平行于长、宽、高。 小蓝希望所…...

计算机求解满足三角形各边数字之和相等的数字填充
圆圈处不重复的填入1至9,使得每条边的四个数字相加的总和相等。 求解思路: 数组中存放1到9的数字,每次随机交换两个数字,构建出新的数字组合,计算这个数字组合是否符合要求。 #include <stdio.h> #include <…...

python魔术方法
魔术方法 魔术方法就是一个类中的方法,和普通方法唯一的不同是普通方法需要调用,而魔术方法是在特定时刻自动触发。这些魔术方法的名字特定,不能更改,但是入口参数的名字可以自己命名。 基本魔术方法 new(cls[,…]) _new_ 是在…...

从0开始学python -48
Python CGI编程-3 CGI中使用Cookie 在 http 协议一个很大的缺点就是不对用户身份的进行判断,这样给编程人员带来很大的不便, 而 cookie 功能的出现弥补了这个不足。 cookie 就是在客户访问脚本的同时,通过客户的浏览器,在客户硬…...

当面试官问我前端可以做的性能优化有哪些
面试过程中面试官问到前端性能优化有哪些,当我咔咔一顿输出之后面试官追问:前端可以做的性能优化有哪些呢? 前端优化大概可以有以下几个方向: 网络优化页面渲染优化JS优化图片优化webpack打包优化React优化Vue优化 网络优化 D…...

一文读懂Java/O流的使用方法和技巧
1.前言 Java 中的 I/O 流是实现输入和输出的一种机制,可以用来读写文件、网络、内存等各种资源。Java 提供了各种类型的流,包括字节流和字符流,以及面向文本和二进制数据的流。在本文中,我们将深入探讨 Java I/O 流的各个方面&am…...

AI for Science系列(二):国内首个基于AI框架的CFD工具组件!赛桨v1.0 Beta API介绍以及典型案例分享!
AI for Science被广泛认为是下一代科研范式,可以有效处理多维度、多模态、多场景下的模拟和真实数据,解决复杂推演计算问题,加速新科学问题发现[1] 。百度飞桨科学计算工具组件赛桨PaddleScience是国内首个公开且可应用于CFD(Comp…...
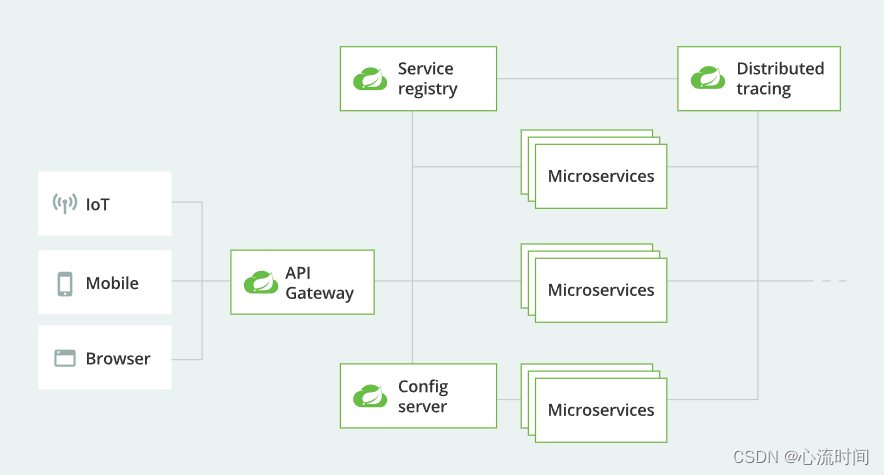
SpringCloud简单介绍
文章目录1. 开源组件2. CAP原则1. 开源组件 功能springcloud netflixspringcloud alibabaspringcloud官方其他服务注册与发现eurekanacosconsulzookeeper负载均衡ribbondubbo服务调用openFeigndubbo服务容错hystrixsentinel服务网关zuulgateway服务配置的同一管理cofig-server…...
《uniapp基础知识》学习笔记Day38-(Period2)全局文件一些常用的配置
如果进行开发的话,首先要配置路由页面 page.json 页面路由 pages.json 文件用来对 uni-app 进行全局配置,决定页面文件的路径、窗口样式、原生的导航栏、底部的原生tabbar 等。 {"pages": [{"path": "pages/component/index…...

APICloud 弹动与滚轴冲突的解决模拟
当打开页面的bounces开关来实现下拉刷新和上翻加载是,如果页面中有scroll-view,那么手指上下滑动时弹动会触发,而滚轴无法正常实现,只有按住不动再拖动滚轴才会触发。开始想通过获取手指点击屏幕的坐标点设置触发条件来解决两者的…...

Spring Cloud(微服务)学习篇(四)
Spring Cloud(微服务)学习篇(四) 1.nacos实现服务之间传参数 1.1 在dto包(shop-sms-api项目)中创建SmsDTO类 package com.zlz.shop.sms.api.dto;import lombok.Data;Data public class SmsDTO {private String tel; }1.2 复制SmsDTO类到shop-sms-server项目的dto包下面 1.3 …...

【Java Pro】001-Java基础:面向对象
【Java Pro】001-Java基础:面向对象 文章目录【Java Pro】001-Java基础:面向对象一、面向对象1、什么是对象现实生活中的对象与程序中的对象2、什么是面向对象面向过程面向对象3、面向过程与面向对象的比较思想方面设计方式方面实现方式方面4、面向过程与…...

ElasticSearch从0到1——基础知识
1.ES是什么? 是一个开源的高扩展的分布式全文检索引擎,它可以近乎实时的存储、检索数据;本身扩展性很好,可以扩展到上百台服务器,处理PB级别的数据使用Java开发并使用Lucene作为其核心来实现所有索引和搜索的功能&…...

【面试系列】equals和==的区别
问题:两个对象值相同(x.equals(y) true),但是可能存在hashCode不同吗? 的定义 比较的是两个对象的内存地址,相等则意味着内存地址一样。 对象的equals方法 Object#equals public boolean equals(Object obj) {return (this obj);}Stri…...

存在重复元素模块-三道题
文章目录存在重复元素217. 存在重复元素219. 存在重复元素 II220. 存在重复元素 III (SortedList二分)小结存在重复元素 217. 存在重复元素 题目链接:217. 存在重复元素 题目大意:给你一个整数数组 nums 。如果任一值在数组中出…...

3种方法删除7-Zip压缩包的密码
7-Zip压缩软件是一款完全免费且开源的软件,不仅能压缩和解压7-Zip压缩包,还能给压缩包设置打开密码。 有些小伙伴可能会遇到这样的问题,7-Zip压缩包设置密码后,过了一段时间不需要密码保护了,或者一不小心忘记了密码&…...

Codeforces Round 855 (Div. 3)(A~F)
A. Is It a Cat?定义满足条件的字符串为:其中仅可能含有meow四种字母的大小写,而且相同种类的字母必须挨在一起,四种字母的顺序必须按照meow排列。给出一个字母串,求是否满足条件。思路:感觉是个很麻烦的模拟。首先把…...
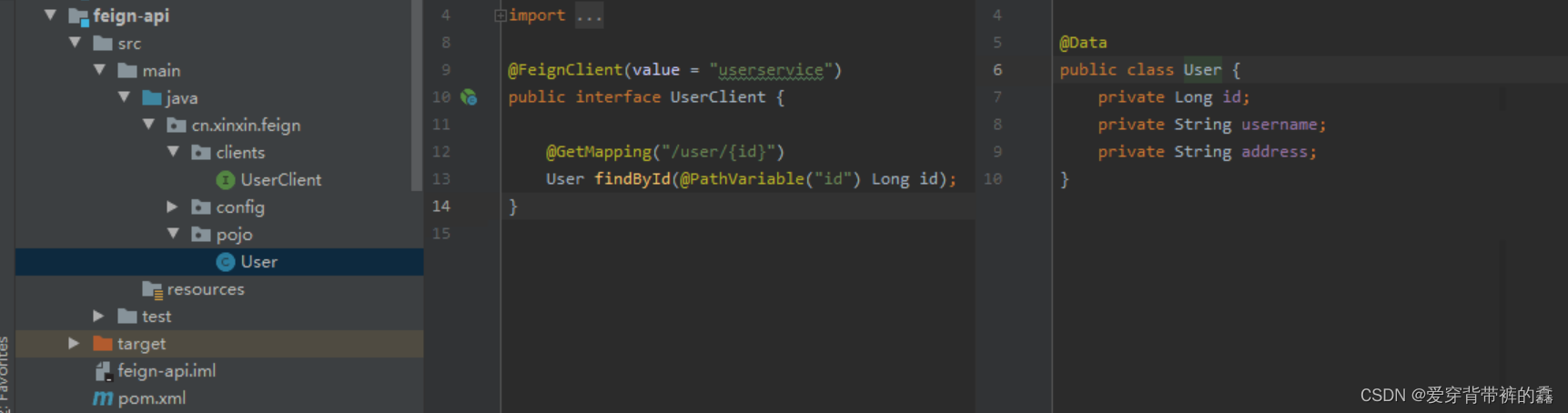
【SpringCloud】SpringCloud详解之Feign实战
目录前言SpringCloud Feign远程服务调用一.需求二.两个服务的yml配置和访问路径三.使用RestTemplate远程调用(order服务内编写)四.使用Feign远程调用(order服务内配置)五.自定义Feign配置(order服务内配置)六.Feign配置日志(oder服务内配置)七.Feign调优(order服务内配置)八.抽…...

tuts4you上lena‘s40个crackme(1)
本来是不打算写文章了,因为懒,想以后通过录屏的形式保存一下自己学的路程。但奈何开学后一直没找到机会,在宿舍也不愿意大吼大叫的讲东西,只好再写写文章了 最近学了一些汇编语言和逆向工程,所以就想通过这40给题目来看…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...

热门Chrome扩展程序存在明文传输风险,用户隐私安全受威胁
赛门铁克威胁猎手团队最新报告披露,数款拥有数百万活跃用户的Chrome扩展程序正在通过未加密的HTTP连接静默泄露用户敏感数据,严重威胁用户隐私安全。 知名扩展程序存在明文传输风险 尽管宣称提供安全浏览、数据分析或便捷界面等功能,但SEMR…...

字符串哈希+KMP
P10468 兔子与兔子 #include<bits/stdc.h> using namespace std; typedef unsigned long long ull; const int N 1000010; ull a[N], pw[N]; int n; ull gethash(int l, int r){return a[r] - a[l - 1] * pw[r - l 1]; } signed main(){ios::sync_with_stdio(false), …...
