K8S--- kubectl auth
该命令可以校验用户或者serviceaccount是否有对应的权限
[root@yyzc-zjjcs01 ~]# /opt/kubernetes/bin/kubectl --kubeconfig /opt/kubernetes/conf/default-admin.kubeconfig auth --help
Inspect authorization
Available Commands:
can-i Check whether an action is allowed
reconcile Reconciles rules for RBAC Role, RoleBinding, ClusterRole, and ClusterRoleBinding objects
Usage:
kubectl auth [flags] [options]
Use “kubectl --help” for more information about a given command.
Use “kubectl options” for a list of global command-line options (applies to all commands).
[root@yyzc-zjjcs01 ~]# /opt/kubernetes/bin/kubectl --kubeconfig /opt/kubernetes/conf/default-admin.kubeconfig auth can-i --help
Check whether an action is allowed.
VERB is a logical Kubernetes API verb like ‘get’, ‘list’, ‘watch’, ‘delete’, etc. TYPE is a Kubernetes resource.
Shortcuts and groups will be resolved. NONRESOURCEURL is a partial URL
相关文章:

K8S--- kubectl auth
该命令可以校验用户或者serviceaccount是否有对应的权限 [root@yyzc-zjjcs01 ~]# /opt/kubernetes/bin/kubectl --kubeconfig /opt/kubernetes/conf/default-admin.kubeconfig auth --help Inspect authorization Available Commands: can-i Check whether an action is allowe…...

HarmonyOS 开发基础(九)forEach
HarmonyOS 开发基础(九)forEach 一、基础使用 Entry Component struct Index {// 创建一个变量,用来存储图片网络网址imageUrl: string https://gw.alicdn.com/imgextra/i2/2201227850912/O1CN01B7gVvP1Ibk6HMiDRz_!!2201227850912.jpg_Q75.…...
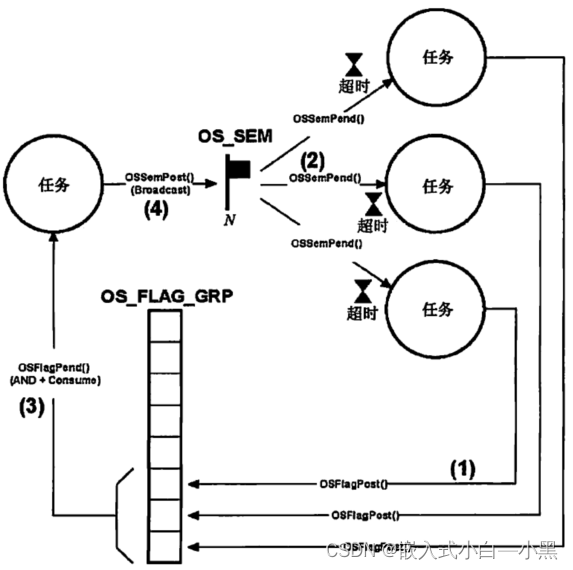
【小黑嵌入式系统第十四课】μC/OS-III程序设计基础(三)——信号量(任务同步资源同步)、事件标记组(与或多个任务)
上一课: 【小黑嵌入式系统第十三课】PSoC 5LP第二个实验——中断控制实验 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站:人工智能 文章目录 1 信号量1.1 简介1.2…...

PMP报考流程?
项目管理相关证书,PMP是一个不错的选择,尤其是小白朋友。 PMP 是项目管理的一个入门证书,理论知识很全面,涵盖了项目管理的全流程,可作为日常工具参考书、完全小白的可以先考一个PMP学好理论,再考一个PRIN…...

【EI会议征稿通知】2024年机器学习与智能计算国际学术会议(MLIC 2024)
2024年机器学习与智能计算国际学术会议(MLIC 2024) 2024 International Conference on Machine learning and intelligent computing 智能计算与机器学习被广泛应用于大数据分析、人工智能、智能制造、智能交通、智能电网、智慧城市、智慧医疗、金融科…...
)
第八篇 提升网页性能:深入解析HTTP请求优化策略(三)
文章目录 1. 缓存策略设计1.1 HTTP缓存机制1.1.1 强缓存(Cache-Control/Expires)1.1.2 协商缓存(ETag/Last-Modified) 1.2 缓存位置1.2.1 浏览器缓存1.2.2 代理服务器缓存 1.3 缓存策略选择1.3.1私有缓存1.3.2 公共资源缓存 1.4 V…...
高版本ant-design动态引用icon
需求 最近在更新自己的博客系统,从 vue2 升到 vue3,同步的也把 ant-design 从 1.7.8 跨越多个大版本升级到了 4.0.8,发现菜单上的 icon 报错了。 查询官方文档发现自从 2.0 版本以后的 icon 就不再支持通过 <a-icon /> 组件动态 type…...

【SQL】delete 与 truncate 命令的区别
区别 truncatedelete属于 DDL(数据定义语言) 范畴属于 DML(数据操作语言) 范畴删除表数据,不能删除视图数据删除表数据,删除视图数据只可以梭哈删除通过 where 进行选择性删除不涉及事务处理删除表中数据涉及事务处理效率高、但无法撤销效率低ÿ…...
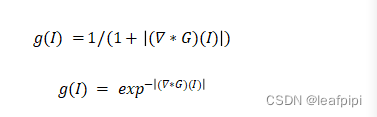
【ITK库学习】使用itk库进行图像分割(四):水平集分割
目录 1、水平集2、itkFastMarchingImageFilter 快速步进分割3、itkShapeDetectionLevelSetImageFilter 快速步进分割 1、水平集 水平集是跟踪轮廓和表面运动的一种数字化方法。基于图像的亮度均值、梯度、边缘特征的微分计算,进行水平集分割。在itk中,所…...
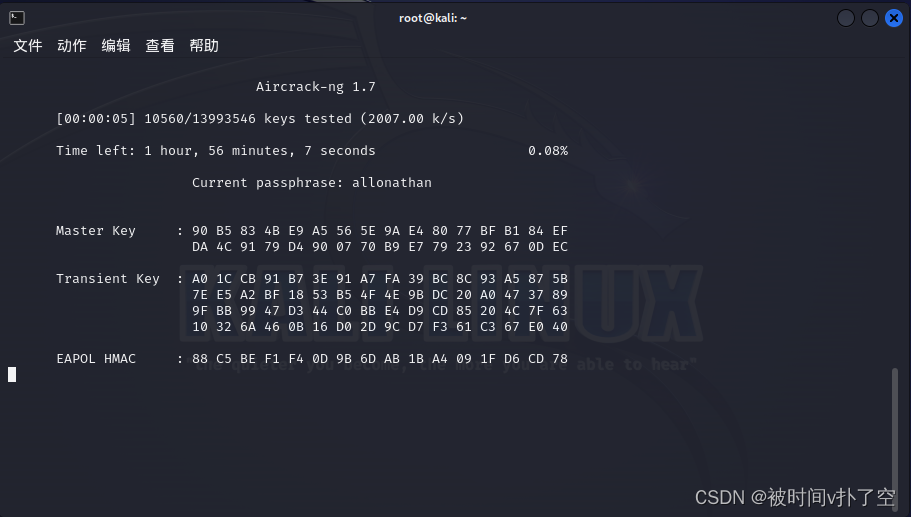
Kali Linux——aircrack-ng无线教程
目录 一、准备 二、案例 1、连接usb无线网卡 2、查看网卡信息 3、开启网卡监听 4、扫描wifi信号 5、抓取握手包 6、强制断开连接 7、破解握手包 三、预防 一、准备 1、usb无线网卡(笔记本也是需要用到) 2、密码字典(Kali 系统自带…...

15.vdo管理
vdo管理 文章目录 vdo管理一、VDO基本概念二、常用操作三、验证VDO卷 一、VDO基本概念 VDO(Virtual Data Optimize虚拟数据优化) 通过压缩或删除存储设备上的数据来优化存储空间。VDO层放置在现有块存储设备例如RAID设备或本地磁盘的顶部。这些块设备也…...
安全漏洞周报(2024.01.01-2023.01.08)
漏洞速览 ■ 用友CRM系统存在逻辑漏洞 漏洞详情 1. 用友CRM系统存在逻辑漏洞 漏洞介绍: 某友CRM系统是一款综合性的客户关系管理软件,旨在帮助企业建立和维护与客户之间的良好关系。它提供了全面的功能,包括销售管理、市场营销、客户服…...
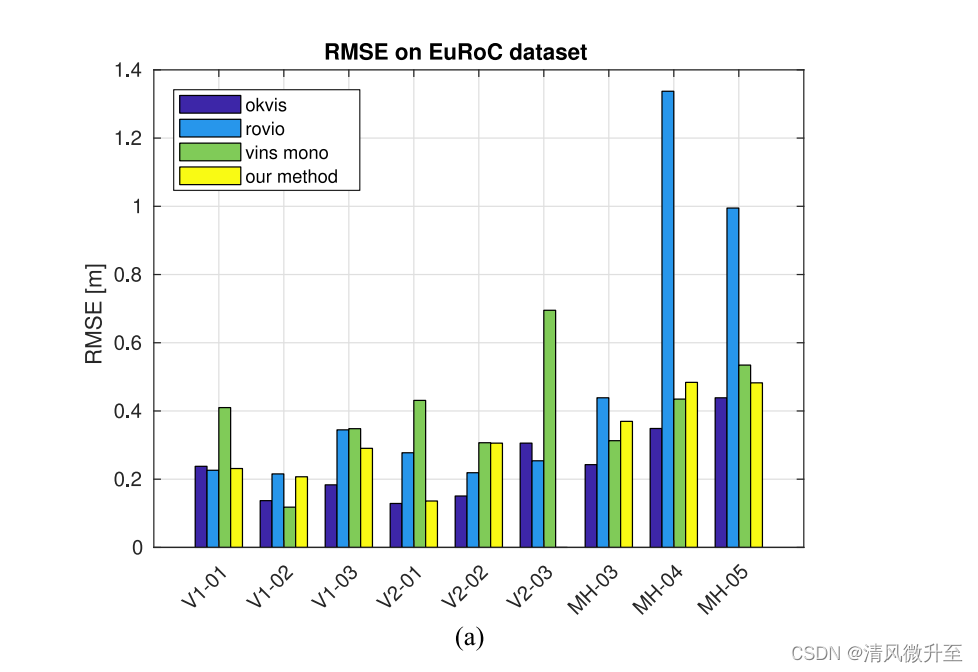
msckf-vio 跑Euroc数据集,并用evo进行评估
所需材料: Euroc数据集主页:https://projects.asl.ethz.ch/datasets/doku.php?idkmavvisualinertialdatasetsevo评估工具代码:https://github.com/MichaelGrupp/evo向msckf-vio中添加保存位姿的代码,可参考https://blog.csdn.ne…...
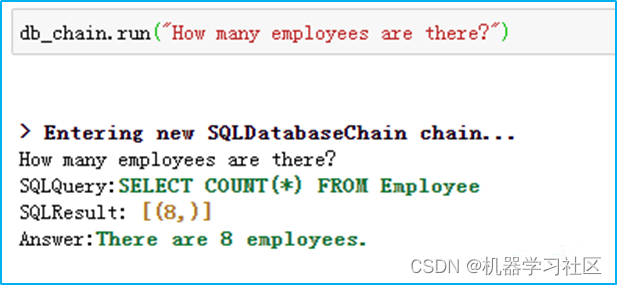
大模型LLM在 Text2SQL 上的应用实践
一、前言 目前,大模型的一个热门应用方向Text2SQL,它可以帮助用户快速生成想要查询的SQL语句,再结合可视化技术可以降低使用数据的门槛,更便捷的支持决策。本文将从以下四个方面介绍LLM在Text2SQL应用上的基础实践。 Text2SQL概…...
)
数据库:园林题库软件(《城市绿地设计规范》答题卷一 )
《城市绿地设计规范》答题卷一 填空题 1、城市绿地设计应贯彻人与自然和谐共存、可持续发展、经济合理等基本原则,创造良好生态和景观效果,促进人的身心健康。 2、城市绿地 urban green space 以植物为主要存在形态,用于改善城市生态&am…...

MySQL之视图外连接、内连接和子查询的使用
目录 一. 视图 1.1 含义 1.2 视图的基本语法 1.3 视图的实操 二. 外连接、内连接和子查询的使用 2.1 SQL脚本 2.2 使用外连接、内连接和子查询进行解答 三. 思维导图 一. 视图 1.1 含义 视图(view)是一种虚拟存在的表,是一个逻辑表&#x…...
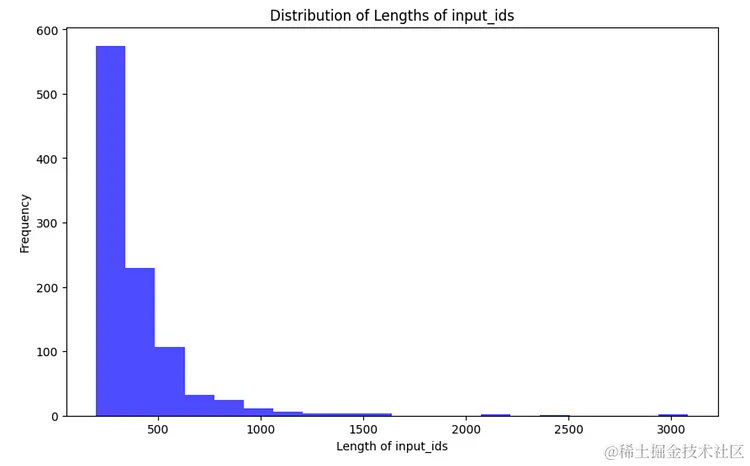
MoE模型性能还能更上一层楼?一次QLoRA微调实践
Fine-Tuning Mixtral 8x7B with QLoRA:Enhancing Model Performance 🚀 编者按:最近,混合专家(Mixture of Experts,MoE)这种模型设计策略展现出了卓越的语言理解能力,如何在此基础上进一步提升 MoE 模型的性能成为业界…...

Java线程学习笔记
1、判断线程存活 1. 当线程run()或者call()方法执行结束,线程进入终止状态 2. 当线程内发生异常,并且异常没有被捕获,线程进入终止状态 3. 线程调用stop()方法后,线程进入终止状态(不推荐使用) 当主线程结束时,其他线程…...
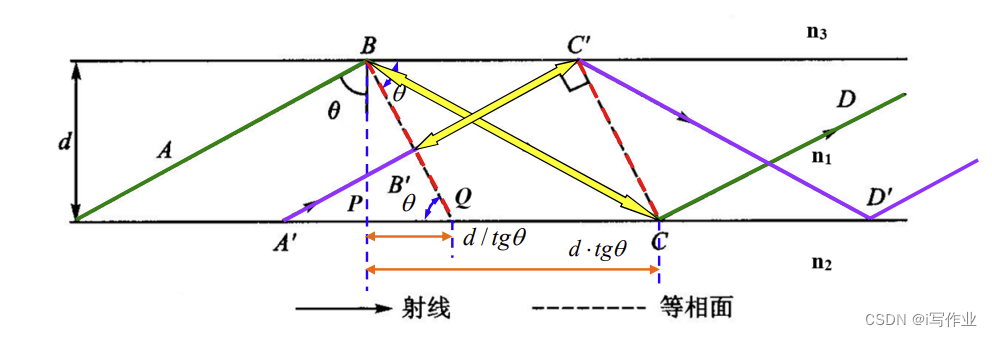
平面光波导_三层均匀平面光波导_射线分析法
平面光波导_三层均匀平面光波导_射线分析法 三层均匀平面光波导: 折射率沿 x x x 方向有变化,沿 y y y、 z z z 方向没有变化三层:芯区( n 1 n_1 n1) > > > 衬底( n 2 n_2 n2) ≥ \geq ≥ 包层( n 3 n_3 n3)包层通常为空…...

IPV6学习记录
IPV6的意义 从广义上来看IPV6协议包含的内容很多: IPV6地址的生成与分配 IPV6的报头的功能内容 IPV4网络兼容IPV6的方案 ICMPv6的功能(融合了arp和IGMP功能) IPV6的路由方式 ipv6的诞生除了由于ipv4的地址枯竭外,很大程度上也是因为ipv4多年的发展产生了很多…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...
