CEC2014:鱼鹰优化算法(Osprey optimization algorithm,OOA)求解CEC2014(提供MATLAB代码
一、鱼鹰优化算法简介
鱼鹰优化算法(Osprey optimization algorithm,OOA)由Mohammad Dehghani 和 Pavel Trojovský于2023年提出,其模拟鱼鹰的捕食行为。

鱼鹰是鹰形目、鹗科、鹗属的仅有的一种中型猛禽。雌雄相似。体长51-64厘米,体重1000-1750克。头部白色,头顶具有黑褐色的纵纹,枕部的羽毛稍微呈披针形延长,形成一个短的羽冠。头的侧面有一条宽阔的黑带,从前额的基部经过眼睛到后颈部,并与后颈的黑色融为一体。上体为暗褐色,略微具有紫色的光泽。下体为白色,胸部的暗色纵纹和飞羽,以及尾羽上相间排列的横斑均极为醒目。虹膜淡黄色或橙黄色,眼周裸露皮肤铅黄绿色,嘴黑色,蜡膜铅蓝色,脚和趾黄色,爪黑色。
鱼鹰栖息于湖泊、河流、海岸或开阔地,尤其喜欢在山地森林中的河谷或有树木的水域地带活动。常见在江河、湖沼及海滨一带飞翔,一见水中有饵,就直下水面,用脚掠之而去。趾具锐爪,趾底遍生细刺,外趾复能由前向后反转,这些都很适于捕鱼。在天气晴朗之日,盘旋于水面上空,定点后俯冲而下,再将捕获的鱼带至岩石、电杆、树上等地方享用。巢常营于海岸或岛屿的岩礁上。主要以鱼为食,有时也捕食蛙、蜥蜴、小型鸟类等其他小型陆栖动物。除了南极和北极,亚洲、北美洲等各大洲均有分布。
1.1鱼鹰优化算法原理
鱼鹰优化算法包含两个阶段:第一阶段为鱼鹰识别鱼的位置并捕鱼(全局勘探), 第二阶段为将鱼带到合适的位置( 局部开采),其详细设计如下:
1.1.1 种群初始化
采用下式随机初始化鱼鹰种群:
X=[X1⋮Xi⋮XN]N×m=[x1,1⋯x1,j⋯x1,m⋮⋱⋮⋱⋮xi,1⋯xi,j⋯xi,m⋮⋱⋮⋱⋮xN,1⋯xN,j⋯xN,m]N×m,xi,j=lbj+ri,j⋅(ubj−lbj),i=1,2,…,N,j=1,2,…,m,\begin{array}{c} X=\left[\begin{array}{c} X_{1} \\ \vdots \\ X_{i} \\ \vdots \\ X_{N} \end{array}\right]_{N \times m}=\left[\begin{array}{ccccc} x_{1,1} & \cdots & x_{1, j} & \cdots & x_{1, m} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ x_{i, 1} & \cdots & x_{i, j} & \cdots & x_{i, m} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ x_{N, 1} & \cdots & x_{N, j} & \cdots & x_{N, m} \end{array}\right]_{N \times m}, \\ x_{i, j}=l b_{j}+r_{i, j} \cdot\left(u b_{j}-l b_{j}\right), i=1,2, \ldots, N, j=1,2, \ldots, m, \end{array}X=X1⋮Xi⋮XNN×m=x1,1⋮xi,1⋮xN,1⋯⋱⋯⋱⋯x1,j⋮xi,j⋮xN,j⋯⋱⋯⋱⋯x1,m⋮xi,m⋮xN,mN×m,xi,j=lbj+ri,j⋅(ubj−lbj),i=1,2,…,N,j=1,2,…,m,
其中,N为鱼鹰的数量,m为问题的维度,初始化位置后依据优化问题计算适应度值:
F=[F1⋮Fi⋮FN]N×1=[F(X1)⋮F(Xi)⋮F(XN)]N×1F=\left[\begin{array}{c} F_{1} \\ \vdots \\ F_{i} \\ \vdots \\ F_{N} \end{array}\right]_{N \times 1}=\left[\begin{array}{c} F\left(X_{1}\right) \\ \vdots \\ F\left(X_{i}\right) \\ \vdots \\ F\left(X_{N}\right) \end{array}\right]_{N \times 1}F=F1⋮Fi⋮FNN×1=F(X1)⋮F(Xi)⋮F(XN)N×1
1.1.2 全局勘探(第一阶段:位置识别和捕鱼)
鱼鹰是强大的猎人,由于其强大的视力,能够探测到水下鱼类的位置。在确定鱼的位置后,他们攻击它并通过潜入水下捕猎鱼。OOA中种群更新的第一阶段是基于对鱼鹰这种自然行为的模拟而建模的。对鱼鹰攻击鱼类进行建模会导致鱼鹰在搜索空间中的位置发生显著变化,这增加了OOA在识别最优区域和逃离局部最优方面的探索能力。在OOA设计中,对于每只鱼鹰,搜索空间中具有较好目标函数值的其他鱼鹰的位置被视为水下鱼类。每只鱼鹰的位置使用下式指定。
FPi={Xk∣k∈{1,2,…,N}∧Fk<Fi}∪{Xbest }\boldsymbol{F P _ { i }}=\left\{X_{k} \mid \boldsymbol{k} \in\{1,2, \ldots, N\} \wedge \boldsymbol{F}_{k}<\boldsymbol{F}_{i}\right\} \cup\left\{\boldsymbol{X}_{\text {best }}\right\}FPi={Xk∣k∈{1,2,…,N}∧Fk<Fi}∪{Xbest }
其中,FPiF P _ { i }FPi为第i只鱼鹰的位置集合,Xbest {X}_{\text {best }}Xbest 为最佳鱼鹰的位置。
鱼鹰随机检测其中一条鱼的位置并攻击它。基于鱼鹰向鱼的运动模拟,使用下式计算相应鱼鹰的新位置。这个新位置,如果它的目标函数的值更好,则替换鱼鹰的先前位置。
xi,jP1=xi,j+ri,j⋅(SFi,j−Ii,j⋅xi,j),xi,jP1={xi,jP1,lbj≤xi,jP1≤ubj;lbj,xi,jP1<lbj;ubj,xi,jP1>ubj.Xi={XiP1,FiP1<Fi;Xi,else ,\begin{array}{l} x_{i, j}^{P 1}=x_{i, j}+r_{i, j} \cdot\left(S F_{i, j}-I_{i, j} \cdot x_{i, j}\right), \\ x_{i, j}^{P 1}=\left\{\begin{array}{ll} x_{i, j}^{P 1}, & l b_{j} \leq x_{i, j}^{P 1} \leq u b_{j} ; \\ l b_{j}, & x_{i, j}^{P 1}<l b_{j} ; \\ u b_{j}, & x_{i, j}^{P 1}>u b_{j} . \end{array}\right. \\ X_{i}=\left\{\begin{array}{l} X_{i}^{P 1}, F_{i}^{P 1}<F_{i} ; \\ X_{i}, \text { else }, \end{array}\right. \\ \end{array}xi,jP1=xi,j+ri,j⋅(SFi,j−Ii,j⋅xi,j),xi,jP1=⎩⎨⎧xi,jP1,lbj,ubj,lbj≤xi,jP1≤ubj;xi,jP1<lbj;xi,jP1>ubj.Xi={XiP1,FiP1<Fi;Xi, else ,
其中,xi,jP1x_{i, j}^{P 1}xi,jP1为第i只鱼鹰在第一阶段时,其第j维的新位置,Fi,jP1F_{i, j}^{P 1}Fi,jP1是其对应的适应度值。SFi,jS F_{i, j}SFi,j为[0,1]之间的随机数,Ii,jI_{i, j}Ii,j为集合{1,2}中的随机数。
1.1.3 局部开采(第二阶段:将鱼带到合适的位置)
捕食鱼后,鱼鹰将其带到合适(对他来说安全)的位置,并在那里吃。OOA中更新种群的第二阶段是基于鱼鹰这种自然行为的模拟建模的。将鱼带到合适位置的建模导致鱼鹰在搜索空间中的位置发生微小变化,从而导致 OOA 在本地搜索中的开发能力增加,并在发现的解决方案附近收敛到更好的解决方案。在OOA的设计中,为了模拟鱼鹰的这种自然行为,首先,针对种群的每个成员,使用下式计算一个新的随机位置作为“适合吃鱼的位置”。然后,如果目标函数的值在这个新位置得到改善,则替换相应鱼鹰的先前位置。
xi,jP2=xi,j+lbj+r⋅(ubj−lbj)t,i=1,2,…,N,j=1,2,…,m,t=1,2,…,T,xi,jP2={xi,jP2,lbj≤xi,jP2≤ubj;lbj,xi,jP2<lbjubj,xi,jP2>ubj,Xi={XiP2,FiP2<Fi;Xi,else ,\begin{array}{c} x_{i, j}^{P 2}=x_{i, j}+\frac{l b_{j}+r \cdot\left(u b_{j}-l b_{j}\right)}{t}, i=1,2, \ldots, N, j=1,2, \ldots, m, t=1,2, \ldots, T, \\ x_{i, j}^{P 2}=\left\{\begin{array}{l} x_{i, j}^{P 2}, l b_{j} \leq x_{i, j}^{P 2} \leq u b_{j} ; \\ l b_{j}, x_{i, j}^{P 2}<l b_{j} \\ u b_{j}, x_{i, j}^{P 2}>u b_{j}, \end{array}\right. \\ X_{i}=\left\{\begin{array}{l} X_{i}^{P 2}, F_{i}^{P 2}<F_{i} ; \\ X_{i}, \text { else }, \end{array}\right. \end{array}xi,jP2=xi,j+tlbj+r⋅(ubj−lbj),i=1,2,…,N,j=1,2,…,m,t=1,2,…,T,xi,jP2=⎩⎨⎧xi,jP2,lbj≤xi,jP2≤ubj;lbj,xi,jP2<lbjubj,xi,jP2>ubj,Xi={XiP2,FiP2<Fi;Xi, else ,
其中,xi,jP2x_{i, j}^{P 2}xi,jP2为第i只鱼鹰在第二阶段时,其第j维的新位置,Fi,jP2F_{i, j}^{P 2}Fi,jP2是其对应的适应度值。rrr为[0,1]之间的随机数,ttt和TTT分别为当前迭代次数和最大迭代次数。
1.2算法描述

1.3算法流程

1.4参考文献
Dehghani Mohammad, Trojovský Pavel.Osprey optimization algorithm: A new bio-inspired metaheuristic algorithm for solving engineering optimization problems[J].Frontiers in Mechanical Engineering,2023,8.
二、CEC2014
CEC2014测试集共有30个单目标测试函数,每个测试函数可选择维度分别为10D、30D、50D、100D。
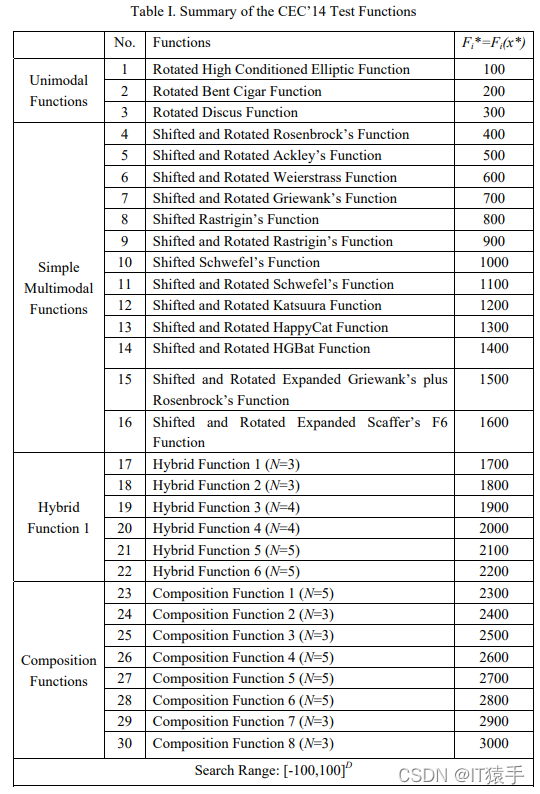
三、求解结果
完整代码添加博客下方博主微信:djpcNLP123
将鱼鹰优化算法OOA法用于求解CEC2014,测试函数维度为30(可根据自己需求更改),种群大小为100,最大迭代次数为50,部分实验结果如下:
close all
clear
clc
SearchAgents_no=100; % 种群大小
Function_name=1; %测试函数1-30
Max_iteration=50; % 最大迭代次数
lb=-100;%变量下界
ub=100;%变量上界
dim=30;%维度 10/30/50/100
[fMin,bestX,curve]=OOA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);
%Draw objective space
semilogy(curve,'Color','g','linewidth',2.5)
legend('OOA')
title(['cec2014-F' num2str(Function_name)])
xlabel('Iteration');
ylabel('Best score obtained so far');
axis tight
grid on
display(['The best solution obtained is : ', num2str(bestX)]);
display(['The best optimal value of the objective funciton is : ', num2str(fMin)]);部分结果如下:
F2

F8

F16

F22

四、参考代码
完整代码添加博客下方博主微信:djpcNLP123
相关文章:

CEC2014:鱼鹰优化算法(Osprey optimization algorithm,OOA)求解CEC2014(提供MATLAB代码
一、鱼鹰优化算法简介 鱼鹰优化算法(Osprey optimization algorithm,OOA)由Mohammad Dehghani 和 Pavel Trojovsk于2023年提出,其模拟鱼鹰的捕食行为。 鱼鹰是鹰形目、鹗科、鹗属的仅有的一种中型猛禽。雌雄相似。体长51-64厘米…...
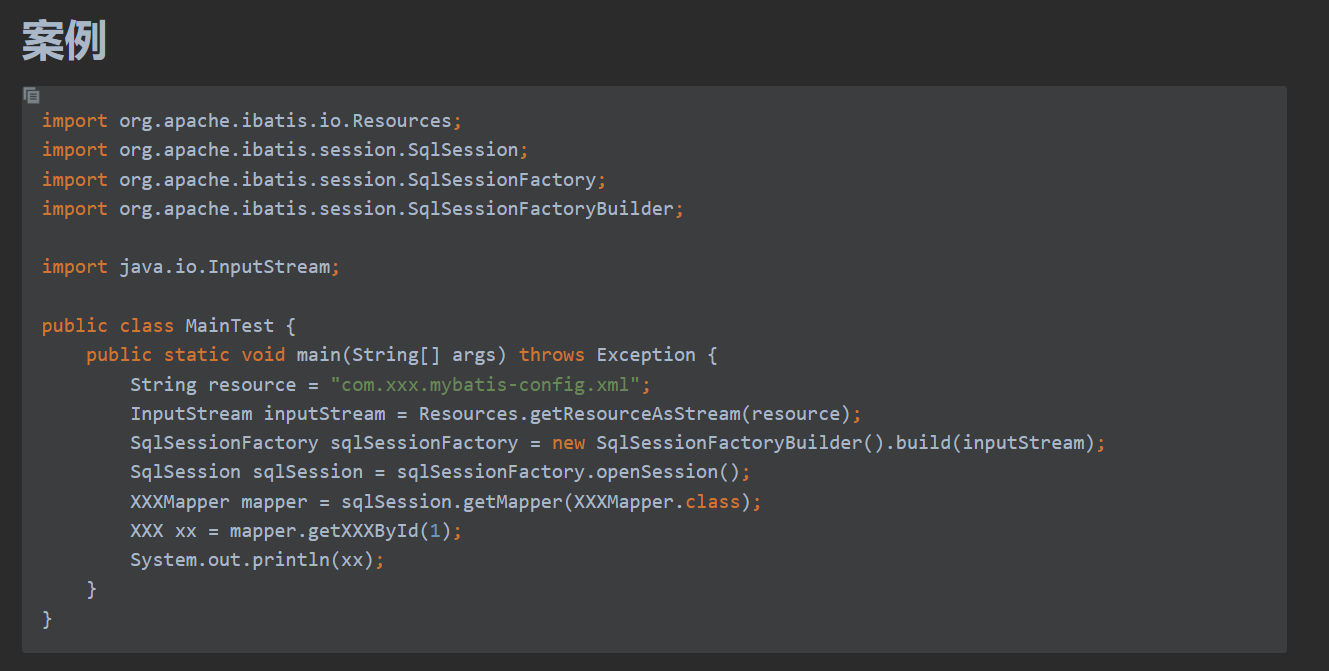
MyBatis底层原理【源码运行时序图】
MyBatis初始化流程🛷 以下代码为例🎉 🎇可对应源码阅读 MyBatis初始化流程✨ #mermaid-svg-yoG1e8Dnp3UIAOUW {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-yoG1e8Dnp3UIAOU…...

k8s 系列之 CoreDNS 解读
k8s 系列之 CoreDNS CoreDNS工作原理 kuberntes 中的 pod 基于 service 域名解析后,再负载均衡分发到 service 后端的各个 pod 服务中,如果没有 DNS 解析,则无法查到各个服务对应的 service 服务 在 Kubernetes 中,服务发现有几…...

从测试鸡蛋硬度到跳表的设计
我回忆起六七年前的一道题鸡蛋掉落问题,有幸在leetCode上找到题目了 原题是2枚鸡蛋 leetCode有拓展,k枚鸡蛋 具体的思路是这样的。 以2枚鸡蛋验证100层为例 不能直接二分查找,因为你在50层测试时,如果直接鸡蛋碎了,那…...
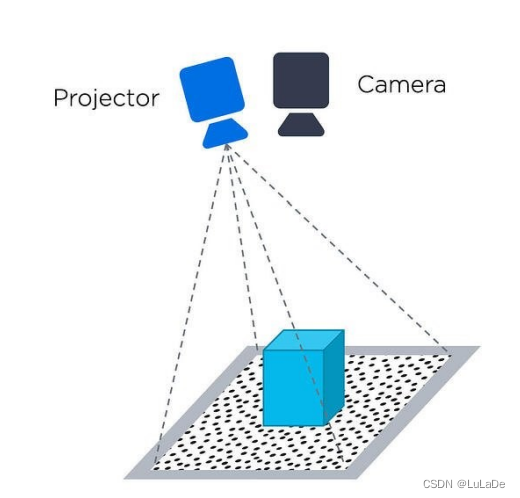
3D立体视觉成像原理介绍【一 】
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录前言什么是基线?基线是如何影响3D图像质量激光三角测量飞行时间结构光相机时间编码结构光前言 本文将介绍3D立体视觉的成像原理,包括【激光三…...

CEC2021:鱼鹰优化算法(Osprey optimization algorithm,OOA)求解CEC2021(提供MATLAB代码
一、鱼鹰优化算法简介 鱼鹰优化算法(Osprey optimization algorithm,OOA)由Mohammad Dehghani 和 Pavel Trojovsk于2023年提出,其模拟鱼鹰的捕食行为。 鱼鹰是鹰形目、鹗科、鹗属的仅有的一种中型猛禽。雌雄相似。体长51-64厘米…...

0301_对应的南京比特物联网
0301_对应的南京比特物联网目录概述需求:设计思路实现思路分析1.流程拓展实现性能参数测试:参考资料和推荐阅读Survive by day and develop by night. talk for import biz , show your perfect code,full busy,skip hardness,make a better …...

钡铼技术BL302 ARM工控机QT图形化界面开发的实践
QT是一种跨平台的应用程序框架,用于开发图形用户界面(GUI)、网络应用程序和嵌入式应用程序。QT提供了丰富的GUI组件和工具,使开发人员能够轻松地创建专业级别的应用程序。QT使用C编写,支持多种操作系统,包括Windows、Linux、macOS…...
)
Python try except异常处理详解(入门必读)
Python 中,用try except语句块捕获并处理异常,其基本语法结构如下所示: try:可能产生异常的代码块 except [ (Error1, Error2, ... ) [as e] ]:处理异常的代码块1 except [ (Error3, Error4, ... ) [as e] ]:处理异常的代码块2 except [Exc…...

信息系统基本知识(三)软件工程
1.4 软件工程 定义:将系统的、规范的、可度量的工程化方法应用于软件开发、运行和维护的全过程即上述方法的研究 软件工程由方法、工具和过程三个部分组成 1.4.1 需求分析 软件需求是指用户对新系统在功能、行为、性能、设计约束等方面的期望。 需求层次 业务…...

Linux下软件部署安装管理----rpmbuild打包rpm包部署安装
来源:微信公众号「编程学习基地」 文章目录1.安装rpmbuild2.rpm包制作打包rpm包3.rpm包安装4.rpm包卸载1.安装rpmbuild yum install rpmbuild yum install rpmdevtools创建rpm包管理路径,生成rpm相关目录 RPM打包的时候需要编译源码,还需要…...
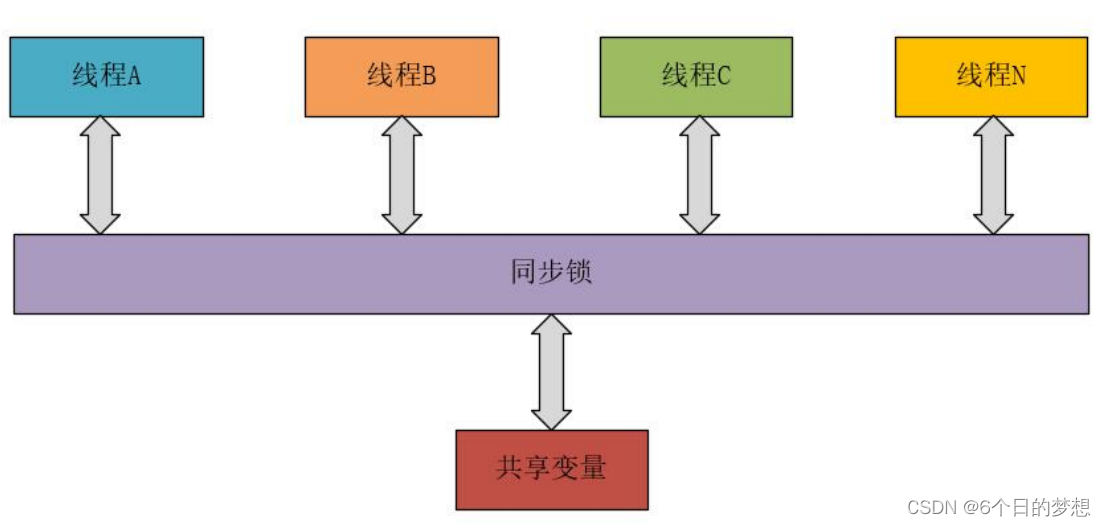
ThreadLocal学会了这些,你也能和面试官扯皮了!
前言 我们都知道,在多线程环境下访问同一个共享变量,可能会出现线程安全的问题,为了保证线程安全,我们往往会在访问这个共享 变量的时候加锁,以达到同步的效果,如下图所示。 对共享变量加锁虽然能够保证线程的安全,但是却增加了开发人员对锁的使用技能,如果锁使用不当…...

【存储】存储特性
存储特性精简配置技术(SmartThin)SmartThin主要功能容量虚拟化存储空间写时分配:Capacity-on-Write读写重定向:Direct-on-Time应用场景及配置流程存储分层技术(SmartTier)存储分层工作原理关键技术容量初始…...
Qt使用OpenGL进行多线程离屏渲染
基于Qt Widgets的Qt程序,控件的刷新默认状况下都是在UI线程中依次进行的,换言之,各个控件的QWidget::paintEvent方法会在UI线程中串行地被调用。若是某个控件的paintEvent很是耗时(等待数据时间CPU处理时间GPU渲染时间)…...
Vue基础入门讲义(三)-指令
文章目录1.什么是指令?2.插值表达式2.1.花括号2.2.插值闪烁2.3.v-text和v-html3.v-model4.v-on4.1.基本用法4.2.事件修饰5.v-for5.1.遍历数组5.2.数组角标5.3.遍历对象6.key7.v-if和v-show7.1.基本使用7.2.与v-for结合7.3.v-else7.4.v-show8.v-bind8.1. 属性上使用v…...
)
pod资源限制,探针(健康检查)
pod资源限制,探针(健康检查)一、资源限制当定义 Pod 时可以选择性地为每个容器设定所需要的资源数量。 最常见的可设定资源是 CPU 和内存大小,以及其他类型的资源当为 Pod 中的容器指定了 request 资源时,调度器就使用…...

Python | 蓝桥杯进阶第一卷——字符串
欢迎交流学习~~ 专栏: 蓝桥杯Python组刷题日寄 蓝桥杯进阶系列: 🏆 Python | 蓝桥杯进阶第一卷——字符串 🔎 Python | 蓝桥杯进阶第二卷——递归(待续) 💝 Python | 蓝桥杯进阶第三卷——动态…...

2023-03-03 mysql列存储-cpu占用100%-追踪思路
摘要: 最近在处理mysql列存储时, 发现在执行explain时, cpu占用达到了100%. 本文分析定位该问题的思路过程 现象: mysqld进程占用100%使用kill processlist终止会话, 无响应查看show processings; 发现一直在运行mysql> show processlist; +----+-----------------+-----…...
JVM—类加载子系统
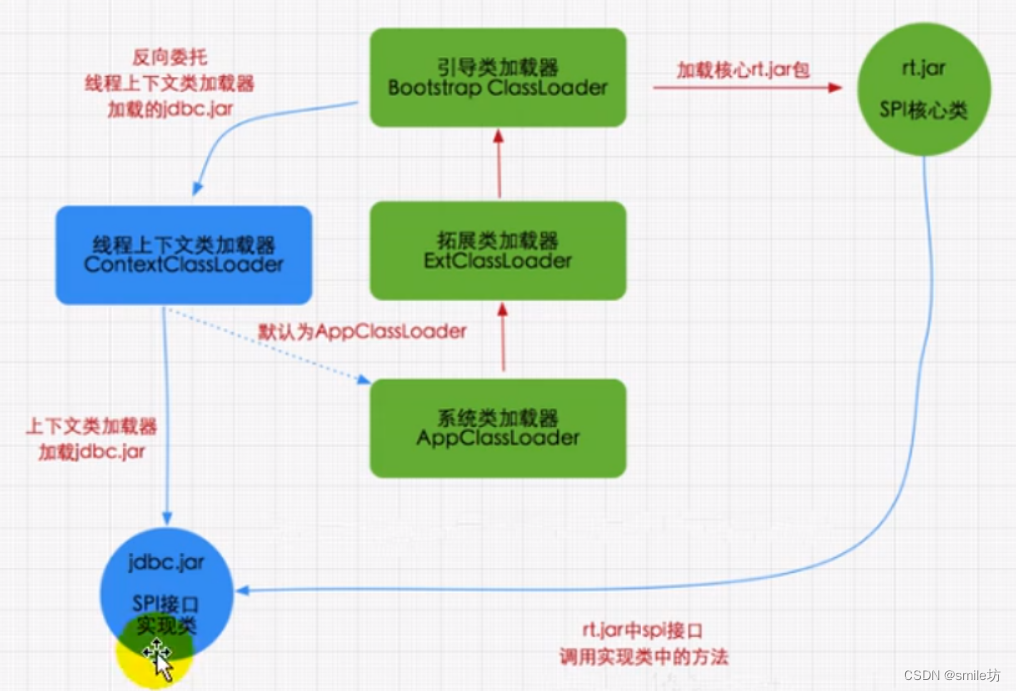
JVM细节版架构图 本文针对Class Loader SubSystem这一块展开讲解类加载子系统的工作流程 类加载子系统作用 1.类加载子系统负责从文件系统或者网络中加载class文件,class文件在文件开头有特定的文件标识即16进制CA FE BA BE; 2.加载后的Class类信息…...

在codeIgniter3中session.php中的数组追加值
如果key是字符串时,输出什么值?会直接把atime()的时间戳添加到key是字符串时,输出什么值?会直接把atime()的时间戳添加到key是字符串时,输出什么值?会直接把atime()的时间戳添加到arr[‘vars’]数组里面&am…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

《Offer来了:Java面试核心知识点精讲》大纲
文章目录 一、《Offer来了:Java面试核心知识点精讲》的典型大纲框架Java基础并发编程JVM原理数据库与缓存分布式架构系统设计二、《Offer来了:Java面试核心知识点精讲(原理篇)》技术文章大纲核心主题:Java基础原理与面试高频考点Java虚拟机(JVM)原理Java并发编程原理Jav…...

深入理解 React 样式方案
React 的样式方案较多,在应用开发初期,开发者需要根据项目业务具体情况选择对应样式方案。React 样式方案主要有: 1. 内联样式 2. module css 3. css in js 4. tailwind css 这些方案中,均有各自的优势和缺点。 1. 方案优劣势 1. 内联样式: 简单直观,适合动态样式和…...

【Qt】控件 QWidget
控件 QWidget 一. 控件概述二. QWidget 的核心属性可用状态:enabled几何:geometrywindows frame 窗口框架的影响 窗口标题:windowTitle窗口图标:windowIconqrc 机制 窗口不透明度:windowOpacity光标:cursor…...
