逆矩阵计算
目录
一、逆矩阵的定义
核心:AB = BA = E
1)定义
2)注意
3)逆矩阵存在的条件|A| != 0
二、核心公式:
三、求逆矩阵(核心考点)
1、伴随矩阵法
2、初等变换法(重点掌握!!)
3、如何理解?
4、什么是初等矩阵?
5、三个基本的初等变换
一、逆矩阵的定义
核心:AB = BA = E
1)定义
A、B为同阶矩阵,如果存在AB = BA = E,即称B为A的逆矩阵,同理,A也是B的逆矩阵。
记作
2)注意
1)不是所有的矩阵都存在逆矩阵
2)只有方阵才存在逆矩阵
3)如果逆矩阵存在,逆矩阵唯一
3)逆矩阵存在的条件|A| != 0
二、核心公式:
三、求逆矩阵(核心考点)
1、伴随矩阵法
这个方法很操蛋,但凡正常理智的人都不会这样去算,因为这是根据公式来计算的,需要计算出|A|和伴随
,计算量可想而知,因此事实上伴随阵就是属于所谓鸡肋,食之无味,弃之可惜。
2、初等变换法(重点掌握!!)
例题:求A的逆矩阵?
1)写出(A,E)

2)利用初等变换,行列均可,将A化成单位阵;同时,右边的单位阵E也进行与A相同的初等变换。通俗来说,就是A怎么变,E也怎么变。举个例子,A中的第1行和第3行交换,E也第1行和第3行交换。最后,当A化为单位阵,E就是。

3、如何理解?
其实非常简单,对于两个矩阵(A,E),
将带进去后:(A
,E
),
你会发现:
A = E
E =
这个括号内的东西,就是我们要求的逆矩阵。
为什么可以这样呢?
因为我们做的一系列的变换,
事实上,本质上,就是对A和E都乘以一个,对不对?
而,要理解这个计算的关键点在于:一个可逆矩阵可以写成一系列初等矩阵的乘积
所以,事实上,我们是将化成了一系列的初等矩阵。
4、什么是初等矩阵?
对单位阵进行一次初等变换所得到的矩阵叫做初等矩阵。
5、三个基本的初等变换
1、某两行(列)交换位置
2、某一行(列)乘某一个数
3、某一行(列)乘以某一个数加到另一行(列)
注意:A左乘一个初等矩阵,相当于对A做相应的初等行变换
A右乘一个初等矩阵,相当于对A做相应的初等列变换
相关文章:
逆矩阵计算
目录 一、逆矩阵的定义 核心:AB BA E 1)定义 2)注意 3)逆矩阵存在的条件|A| ! 0 二、核心公式: 三、求逆矩阵(核心考点) 1、伴随矩阵法 2、初等变换法(重点掌握ÿ…...

《豫鄂烽火燎原大小焕岭》:一部穿越时空的历史史诗
《豫鄂烽火燎原大小焕岭》:一部穿越时空的历史史诗 一部赓续红色血脉的生动教材 一部讴歌时代英雄和人民精神宝典 当历史的烽烟渐渐远去,留下的是一页页泛黄的记忆和无数英雄的壮丽诗篇。李传铭的力作《豫鄂烽火燎原大小焕岭》正是这样一部深情的回望&am…...

浅研究下 DHCP 和 chrony
服务程序: 1.如果有默认配置,请先备份,再进行修改 2.修改完配置文件,请重启服务或重新加载配置文件,否则不生效 有些软件,安装包的名字和系统里服务程序的名字不一样(安装包名字:…...
【算法】动态中位数(对顶堆)
题目 依次读入一个整数序列,每当已经读入的整数个数为奇数时,输出已读入的整数构成的序列的中位数。 输入格式 第一行输入一个整数 P,代表后面数据集的个数,接下来若干行输入各个数据集。 每个数据集的第一行首先输入一个代表…...

mysql服务多实例运行
1、官网下载mysql安装包 https://downloads.mysql.com/archives/community/ 2、解压安装包 tar -zxvf mysql-8.1.0-linux-glibc2.28-aarch64.tar.xz -C /usr/localmv /usr/local/mysql-8.1.0-linux-glibc2.28-aarch64 /usr/local/mysql 3、创建mysql用户组 groupadd…...

「HDLBits题解」Module fadd
本专栏的目的是分享可以通过HDLBits仿真的Verilog代码 以提供参考 各位可同时参考我的代码和官方题解代码 或许会有所收益 题目链接:Module fadd - HDLBits module top_module (input [31:0] a,input [31:0] b,output [31:0] sum );//wire [15:0] t1, t2 ; wire co…...
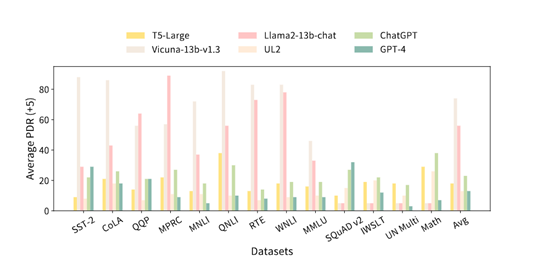
微软等开源评估ChatGPT、Phi、Llma等,统一测试平台
微软亚洲研究院、中国科学院自动化研究所、中国科学技术大学和卡内基梅隆大学联合开源了,用于评估、分析大语言模型的统一测试平台——PromptBench。 Prompt Bench支持目前主流的开源、闭源大语言模型,例如,ChatGPT、GPT-4、Phi、Llma1/2、G…...
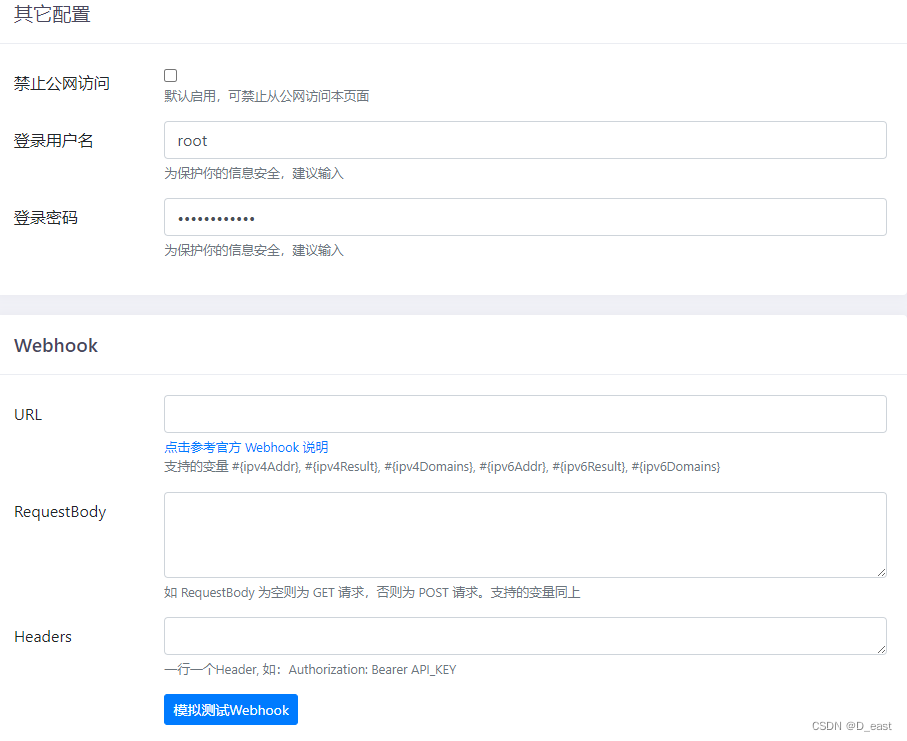
DDNS-GO配置使用教程
环境:openwrt 下载地址:Releases jeessy2/ddns-go GitHub 下载 ssh至openwrt根目录,根据你的处理器选择要下载的版本,我是路由器,选择的是 ddns-go_5.7.1_linux_arm64.tar.gz wget github链接 安装 tar -zxvf…...

flex弹性盒子常用的布局属性详解
想必大家在开发中经常会用到flex布局。而且还会经常用到 justify-content 属性实现分栏等等 接下来给大家分别讲一下 justify-content 的属性值。 以下是我敲的效果图大家可以清晰看出区别 space-between 属性值可以就是说两端对齐 space-evenly 属性值是每个盒子之间的…...
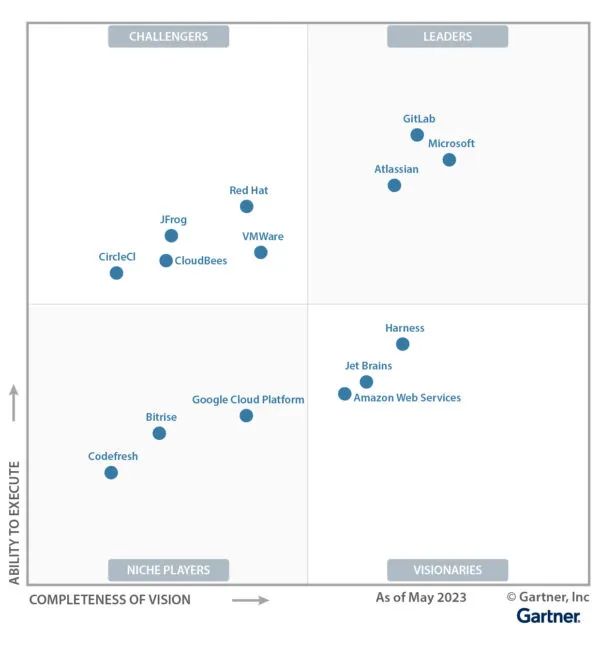
2023年Gartner® DevOps平台魔力象限发布,Atlassian被评为“领导者”
Atlassian在2023年Gartner魔力象限的DevOps平台评选中,被评为领导者。 Gartner根据执行能力和愿景的完整性,对全球14家DevOps平台提供商进行了评估,并发布2023年Gartner魔力象限。其中,Atlassian被评为领导者。 Atlassian提供了一…...
kylin集群使用nginx反向代理
前文已经提到,我安装了kylin集群。 kylin3集群问题和思考(单机转集群)-CSDN博客文章浏览阅读151次,点赞3次,收藏6次。由于是同一个集群的,元数据没有变化,所以,直接将原本的kylin使用…...
小红书搜索团队提出全新框架:验证负样本对大模型蒸馏的价值
大语言模型(LLMs)在各种推理任务上表现优异,但其黑盒属性和庞大参数量阻碍了它在实践中的广泛应用。特别是在处理复杂的数学问题时,LLMs 有时会产生错误的推理链。传统研究方法仅从正样本中迁移知识,而忽略了那些带有错…...

汽车销售领域相关专业术语
引言 本文是笔者在从事汽车销售领域信息化建设过程,积累的一些专业术语注解,供诸位参考交流。 专业术语清单 4S店 汽车销售服务4S店;是由经销商投资建设,按照汽车生产厂家规定的标准建造,是一种集整车销售(Sale)、零配件(Sparepart)、售后服务(Service)、信息…...

代币合约 ERC20 Token接口
代币合约 在以太坊上发布代币就要遵守以太坊的规则,那么以太坊有什么规则呢?以太坊的精髓就是利用代码规定如何运作,由于在以太坊上发布智能合约是不能修改和删除的,所以智能合约一旦发布,就意味着永久有效,不可篡改…...

判断回文字符串—C语言
题目要求 输入一个字符串,判断该字符串是否为回文。回文就是字符串中心对称,从左向右读和从右向左读的内容是一样的。 输入格式: 输入在一行中给出一个不超过80个字符长度的、以回车结束的非空字符串。 输出格式: 输出在第1行中…...
如何在Docker本地搭建流程图绘制神器draw.io并实现公网远程访问
推荐 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站 前言 提到流程图,大家第一时间可能会想到Visio,不可否认,VIsio确实是功能强大,但是软…...

Web前端篇——el-timeline+el-scrollbar时间轴数据刷新后自动显示滚动条
背景:使用el-timelineel-scrollbar显示时间轴,当时间轴数据刷新时,el-scrollbar滚动条会自动隐藏。 当给el-scrollbar设置了永久显示滚动条(如下代码),以为可以一劳永逸,发现问题仍然存在。 .…...

Flutter 监听前台和后台切换的状态
一 前后台的切换状态监听 混入 WidgetsBindingObserver 这个类,这里提供提供了程序状态的一些监听 二 添加监听和销毁监听 overridevoid initState() {super.initState();//2.页面初始化的时候,添加一个状态的监听者WidgetsBinding.instance.addObserver…...
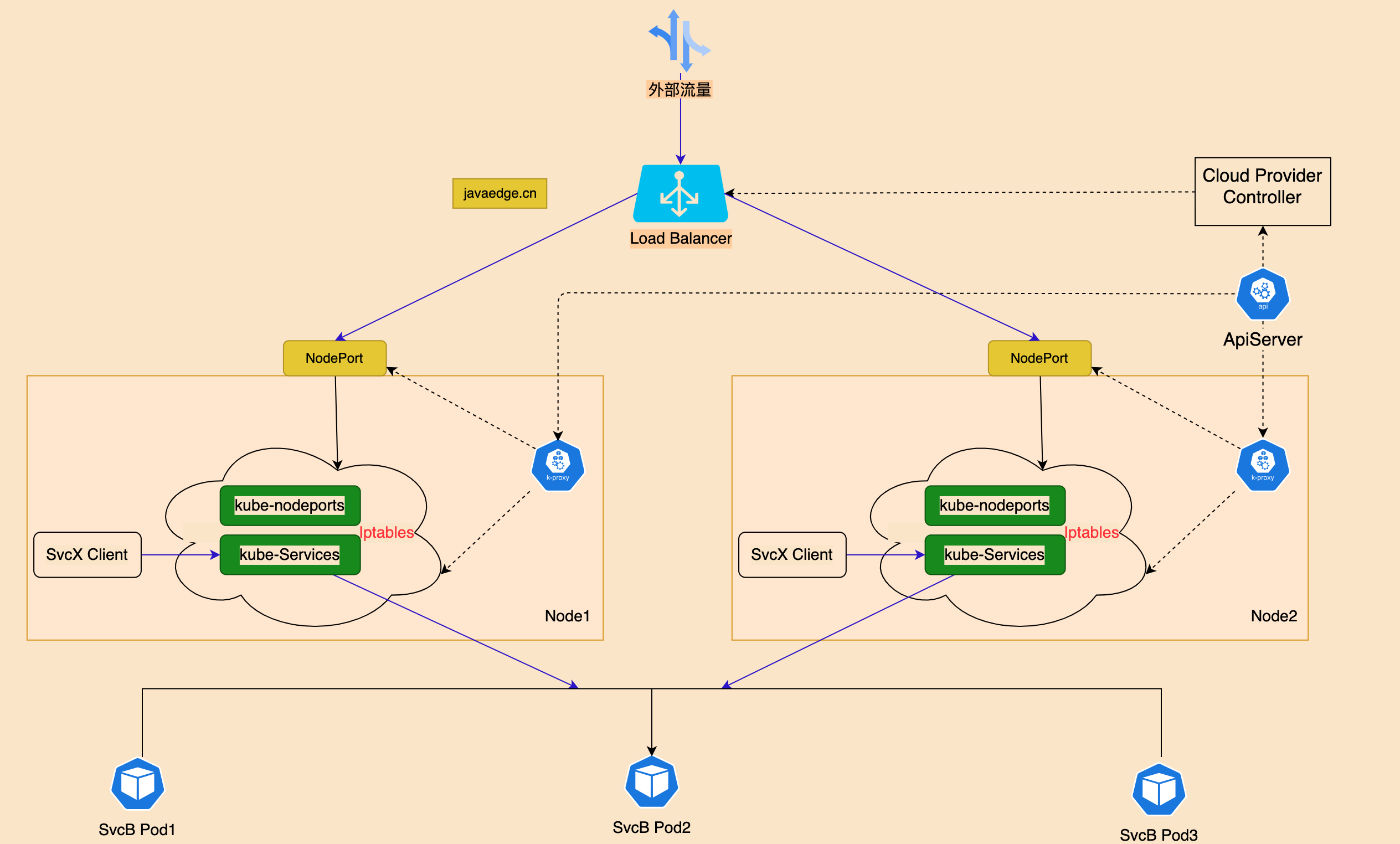
图解Kubernetes的服务(Service)
pod 准备: 不要直接使用和管理Pods: 当使用ReplicaSet水平扩展scale时,Pods可能被terminated当使用Deployment时,去更新Docker Image Version,旧Pods会被terminated,然后创建新Pods 0 啥是服务…...

facebook广告素材制作要注意哪些
在制作Facebook广告素材时,需要注意以下几点: 目标受众:了解目标受众的喜好、需求和兴趣,以便制作能够吸引他们的广告素材。广告格式:选择适合广告内容的格式,如图片、视频、幻灯片等。同时,要…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...
