【光波电子学】基于MATLAB的多模光纤模场分布的仿真分析
基于MATLAB的多模光纤模场分布的仿真分析
一、引言
(1)多模光纤的概念
多模光纤(MMF)是一种具有较大纤芯直径的光纤结构,其核心直径通常在10-50微米范围内。与单模光纤(SMF)相比,多模光纤可以容纳多个光信号模式传播,因此在许多应用中具有广泛的用途。
多模光纤的工作原理基于多个光模式在纤芯中的传播。每个光模式可以看作是一个光束,具有自己的传播方向和相位。在传输过程中,这些模式会互相干涉,导致在光纤尾部出现光场分布的变化。多模光纤主要由纤芯、包层和护层组成。纤芯用于传输光信号,而包层则用于限制光信号的传播范围,并减小光信号的损耗。
多模光纤的优点是可以传输大量的光信号,适用于需要高通量和高带宽的应用。此外,由于纤芯直径较大,制造成本相对较低。多模光纤也可以与其他光学器件(如光学耦合器和分束器)结合使用,进一步扩展其应用领域。然而,多模光纤的缺点是存在多个模式的干涉和色散问题。这会导致信号失真和传输速率的降低,在一些对信号质量要求较高的应用中可能限制了其使用。
(2)实现多模光纤的方法及优缺点
实现多模光纤的方法主要包括两种:径向抽运和溅射法。
径向抽运是一种常用的方法,通过使用高能激光束沿纤芯径向照射的方式,来改变纤芯的折射率分布。从而形成多个模式的分布。这种方法简单易行,可以在现有光纤基础上进行改造,只需通过特定的激光参数进行调节即可得到所需的多模光纤结构。但是,这种方法存在光强不均匀的问题,可能导致光信号的耦合效率下降。
溅射法是另一种常用的方法,它通过将带有特殊结构的材料溅射在纤芯表面来实现多模光纤的制造。这种方法可以灵活调节纤芯的形状和尺寸,从而得到更好的纤芯折射率分布。这种方法的优点是制备过程较为简单,可以获得较为均匀的多模分布。然而,溅射法的缺点是制备过程较为复杂,需要使用特殊的设备和工艺,并且制备成本相对较高。
(3)仿真多模光纤模场分布方法及优缺点
多模光纤模场分布仿真的常用方法分为基于有限元法的分析方法、基于模式耦合方程的分析方法、基于光线追迹法的分析方法。首先,基于有限元法的分析方法能处理各种光纤结构,得到高精度的结果,但算法复杂,计算耗时长。其次,基于模式耦合方程的分析方法凭借其精确性和强大的理论基础,适用于各种光纤结构,但数值求解较复杂。最后,基于光线追迹法的分析方法简单且计算速度快,适用于简单光纤结构,但处理复杂光学现象能力有限。因此,在选择仿真方法时需综合考虑光纤结构、精度需求和计算资源等因素。对于精度要求较高且计算资源充足的情况,可以采用有限元法或模式耦合方程方法;而在时间和计算资源有限的情况下,可选择光线追迹法作为快速的近似方法。总之,在仿真多模光纤模场分布问题中,不同的方法各有优劣,需要根据具体情况选择合适的方法以达到较准确的结果。
本实验将采用基于模式耦合方程的分析方法。在弱导近似下,可以利用模式耦合方程来分析由 H E l + 1 , m HE_{l+1,m} HEl+1,m模和 E H l − 1 , m EH_{l-1,m} EHl−1,m模组合的模式,进而得到线性偏振模式 L P l m LP_{lm} LPlm。模式耦合方程方法适用于光纤中光模式的耦合和传输过程,能够较准确地描述复杂的光场分布情况,因此适合用于分析这种模式的组合。
二、理论基础
2.1 多模光纤模式
在多模光纤中,光可以以多种不同的模式传播,每种模式对应着不同的空间分布和频率。多模光纤中的模式可以通过横向电场分布和纵向电场分布来描述。对于多模光纤,一般将其横截面划分成许多模式场,每个模式都对应着一个特定的传输方式和特征模场分布。设直径为d的多模光纤,其模式可以用以下数学公式表示:
V = 2 π n a λ n 1 2 − n 2 2 V = \frac{{2 \pi n a}}{\lambda} \sqrt{n_1^2 - n_2^2} V=λ2πnan12−n22
其中,V是光的归一化频率参数,n是光纤的折射率,a是光纤的半径,λ是光的波长,n1和n2分别是光纤的内层和外层折射率。
2.2 模场分布的描述
光纤中的模式分布是指光场在空间中的分布特性,在多模光纤中,模式分布描述了光场的横向和纵向分布特性,可以通过横向和纵向电场分布函数来表示模式的光场分布。
横向电场分布描述了光纤中横向方向上的电场强度分布特性,一般可用Hermite-Gaussian函数或Laguerre-Gaussian函数数学公式来表示。Hermite-Gaussian 函数是描述横向模式的一类基函数,而 Laguerre-Gaussian 函数则广泛用于描述更复杂的模式,例如旋转和角动量。这些函数是解波动方程后得到的特定形式的解,可以描述不同类型的模式在横向方向上的分布特性。
纵向电场分布描述了光场沿光纤轴向的分布特性,可用传输矩阵法等数学方法求解得到。光场的纵向分布特性对于光纤的传输和耦合等性能具有重要影响,因此对其进行准确的描述和仿真分析至关重要。
光场分布的描述可以帮助理解光在多模光纤中的传输特性,包括光的衍射、色散、耦合损耗等现象。通过数学模型和仿真分析,可以得到光场在光纤中的传输特性。
(1)Hermite-Gaussian 函数
Hermite-Gaussian 函数描述的是横向电场分布,它可以用于多模光纤中的光波的横向模式。Hermite-Gaussian 函数可以表示为:
H m n ( x , y ) = 1 σ x σ y H m ( 2 x σ x ) H n ( 2 y σ y ) e − x 2 σ x 2 e − y 2 σ y 2 H_{mn}(x, y) = \frac{1}{\sigma_x \sigma_y} H_m(\frac{\sqrt{2}x}{\sigma_x}) H_n(\frac{\sqrt{2}y}{\sigma_y}) e^{-\frac{x^2}{\sigma_x^2}} e^{-\frac{y^2}{\sigma_y^2}} Hmn(x,y)=σxσy1Hm(σx2x)Hn(σy2y)e−σx2x2e−σy2y2
其中, H m H_m Hm 和 H n H_n Hn是 Hermite 多项式, σ x \sigma_x σx 和 σ y \sigma_y σy是横向方向的标准偏差。 H m n ( x , y ) H_{mn}(x, y) Hmn(x,y) 描述了光波在横向空间的电场分布,其中的 m 和n 是与模式密切相关的整数指数。
(2)Laguerre-Gaussian 函数
Laguerre-Gaussian 函数描述的是光波的纵向电场分布,它包含了更丰富和复杂的模式信息。Laguerre-Gaussian 函数可以表示为:
L G p , l ( r , θ , z ) = A ( 2 π r w ( z ) ) ∣ l ∣ L p ∣ l ∣ ( 2 r 2 w 2 ( z ) ) e − r 2 w 2 ( z ) e − i k z e i l θ LG_{p,l}(r, \theta, z) = A \left( \sqrt{\frac{2}{\pi}} \frac{r}{w(z)} \right)^{|l|} L_p^{|l|}\left( \frac{2r^2}{w^2(z)} \right) e^{-\frac{r^2}{w^2(z)}} e^{-ikz} e^{il\theta} LGp,l(r,θ,z)=A(π2w(z)r)∣l∣Lp∣l∣(w2(z)2r2)e−w2(z)r2e−ikzeilθ
其中,A是归一化系数, w(z) 是 Gauss 横向束腰半径, L p ∣ l ∣ L_p^{|l|} Lp∣l∣是以 L p L_p Lp表示的关联 Laguerre 多项式,r 和 θ \theta θ分别是极坐标下的径向距离和角度,z是传输距离,k是波矢,而 l 和p是与光波的角动量和径向指数相关的整数。
Laguerre-Gaussian 函数能够描述光波在光纤中的传播行为、角动量以及形成复杂模式的能力。这种函数是为了解决高斯光束的纵向传输而引入的,可在光纤的输出端获得与其横向电场分布相关的模式信息。
三、MATLAB仿真模型设计
% 参数设置
a = 25e-6; % 光纤核径 (25微米)
lambda = 1550e-9; % 光波长 (1550 nm)
n_core = 1.45; % 核心折射率
n_cladding = 1.44; % 包层折射率
V = 2.405; % V参数, 通常由 a, lambda 和 n_core, n_cladding确定
delta = (n_core^2 - n_cladding^2)/(2*n_core^2); % 相对折射率差% 选定模式对应的 l 和 m
l = 1;
m = 1;% Hermite-Gaussian函数参数
M = 1; % Hermite-Gaussian x方向模式数
N = 1; % Hermite-Gaussian y方向模式数% 网格设置
r_max = 5*a; % 设置画图半径为光纤核半径的5倍
points = 200; % 分辨率
[x, y] = meshgrid(linspace(-r_max, r_max, points), linspace(-r_max, r_max, points));
r = sqrt(x.^2 + y.^2);
phi = atan2(y,x);% HE和EH模式的振幅系数
A_he = V * sqrt(2/(pi * factorial(l) * 2^l)) * (sqrt(2) * r/a).^l ....* exp(-r.^2/a^2) .* cos(l * phi);
A_eh = V * sqrt(2/(pi * factorial(l) * 2^(l-2))) * (sqrt(2) * r/a).^(l-2) ....* exp(-r.^2/a^2) .* cos((l-2) * phi);% LP模式的横向电场分布 (HE, EH模式的线性组合)
E_transverse = A_he + A_eh;% 采用传输矩阵法求解纵向电场分布
k0 = 2 * pi / lambda; % 自由空间波数
gamma = sqrt(n_core^2*k0^2 - (l*pi/(2*a))^2 - (m*pi/(2*a))^2); % 衰减常数
z = linspace(0, 10e-3, 500); % z方向网格
E_longitudinal = exp(-1i*gamma*z); % 纵向电场分布% 横向电场分布的可视化
figure(1);
imagesc(linspace(-r_max, r_max, points)*1e6, linspace(-r_max, r_max, points)*1e6, abs(E_transverse).^2);
axis square;
xlabel('x (μm)');
ylabel('y (μm)');
title('横向电场分布 |E_{trans}|^2 of LP_{1,1}');
colorbar;% 纵向电场分布的可视化
figure(2);
plot(z*1e3, abs(E_longitudinal).^2);
xlabel('Propagation distance z (mm)');
ylabel('|E_{long}|^2');
title('纵向电场分布 |E_{long}|^2 of LP_{1,1} ');





四、仿真结果分析
4.1 不同模式的光场分布
在仿真中可以观察到不同模式的光场分布。其中,代码中通过修改变量l,可以选择不同的模式数,对应于不同的径向模式。然后,通过使用Hermite-Gaussian函数和选择的模式数,计算对应的横向电场分布。最后,通过传输矩阵法求解纵向电场分布。对于给定的光纤参数,通过修改l参数,可以选择不同的模式。结果中的图像展示了横向和纵向电场的分布情况。横向电场分布显示在上方的图像,图像的坐标轴表示在光纤横向平面内的位置。纵向电场分布显示在下方的图像,图像的横坐标表示传播距离,纵坐标表示电场的强度。通过观察这些图像,可以清晰地看到不同模式之间的差异。对于较低的模式数,光场分布呈现出类似高斯光束的形状,即光束在光纤径向上的分布类似高斯分布。而对于较高的模式数,光场分布呈现出更多的波峰和波谷,形成一种更复杂的结构。
4.2 参数对模场分布的影响
光场分布受到光纤参数的影响。在给定的代码中,可以通过修改光纤的核径、光波长、核心折射率和包层折射率来改变光纤的参数。在这些参数的不同取值下,仿真可以得出不同的光场分布情况。例如,核径的变化会导致光场分布的形状和尺寸的变化。较大的核径会导致光场分布的尺寸扩大,而较小的核径则会使其更加集中。此外,光波长的变化也会对光场分布产生影响。较短的光波长会导致光场分布的精细结构变得更加明显,而较长的光波长则会使其变得模糊一些。光纤的核心折射率和包层折射率对模场分布也有重要影响。它们之间的差异决定了相对折射率差的值。较大的相对折射率差会导致光场在光纤中的传播受到更明显的限制,形成更复杂的光场分布。通过对这些参数的改变,可以进一步理解光场在光纤中的传播行为,并优化光纤设计以满足不同应用需求。
相关文章:

【光波电子学】基于MATLAB的多模光纤模场分布的仿真分析
基于MATLAB的多模光纤模场分布的仿真分析 一、引言 (1)多模光纤的概念 多模光纤(MMF)是一种具有较大纤芯直径的光纤结构,其核心直径通常在10-50微米范围内。与单模光纤(SMF)相比,…...

0104 AJAX介绍
Ajax 的全称是 Asynchronous Javascript And XML (异步 JavaScript 和 XML )。 通俗的理解:在网页中利用 XMLHttpRequest 对象和服务器进行数据交互的方式,就是 Ajax Ajax 能让我们轻松实现网页与服务器之间的数据交互。 浏览器…...
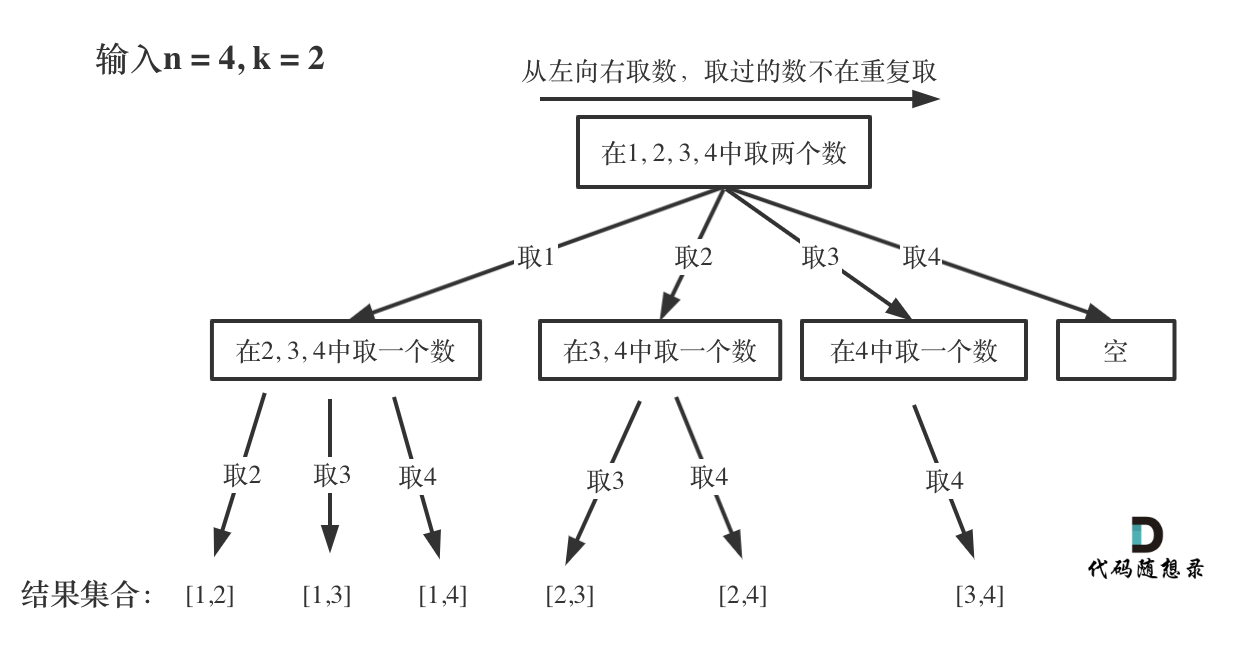
代码随想录算法训练营第24天 | 理论基础 77. 组合
目录 理论基础 什么是回溯法 回溯法的效率 回溯法解决的问题 如何理解回溯法 回溯法模板 77. 组合 💡解题思路 💻实现代码 理论基础 什么是回溯法 回溯法也可以叫做回溯搜索法,它是一种搜索的方式。 回溯法的效率 虽然回溯法很难ÿ…...

【深度学习环境搭建】Windows搭建Anaconda3、已经Pytorch的GPU版本
目录 搭建Anaconda3搭建GPU版本的Pytorch你的pip也要换源,推荐阿里源打开conda的PowerShell验证 搭建Anaconda3 无脑下载安装包安装(自行百度) 注意点: 1、用户目录下的.condarc需要配置(自定义环境的地址(…...

基于WebFlux的Websocket的实现,高级实现自定义功能拓展
基于WebFlux的Websocket 一、导入XML依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-webflux</artifactId> </dependency><!-- 或者引入jackson --> <dependency><group…...

使用 LLVM clang C/C++ 编译器编译 OpenSSL 3.X库
1、下载 OpenSSL 3.X 库的源代码放到待编译目录 2、解压并接入 OpenSSL 3.X 库源码的根目录 3、复制 ./Configure 一个取名为 ./Configure-clang 4、修改 ./Configure-clang 找到配置段: CC CXX CPP LD 把它们改成 CC > "/usr/bin/clang-…...

【信息安全】hydra爆破工具的使用方法
hydra简介 hydra又名九头蛇,与burp常规的爆破模块不同,hydra爆破的范围更加广泛,可以爆破远程桌面连接,数据库这类的密码。他在kali系统中自带。 参数说明 -l 指定用户名 -L 指定用户名字典文件 -p 指定密码 -P 指…...

uniapp中uview组件库丰富的CountTo 数字滚动使用方法
目录 #平台差异说明 #基本使用 #设置滚动相关参数 #是否显示小数位 #千分位分隔符 #滚动执行的时机 #API #Props #Methods #Event 该组件一般用于需要滚动数字到某一个值的场景,目标要求是一个递增的值。 注意 如果给组件的父元素设置text-align: cente…...

inflate流程分析
一.inflate的三参数重载方法else里面逻辑 我们先看到setContentView里面的inflate的调用链: public View inflate(LayoutRes int resource, Nullable ViewGroup root) {return inflate(resource, root, root ! null);}public View inflate(LayoutRes int resource…...

数据挖掘实战-基于机器学习的电商文本分类模型
🤵♂️ 个人主页:艾派森的个人主页 ✍🏻作者简介:Python学习者 🐋 希望大家多多支持,我们一起进步!😄 如果文章对你有帮助的话, 欢迎评论 💬点赞Ǵ…...
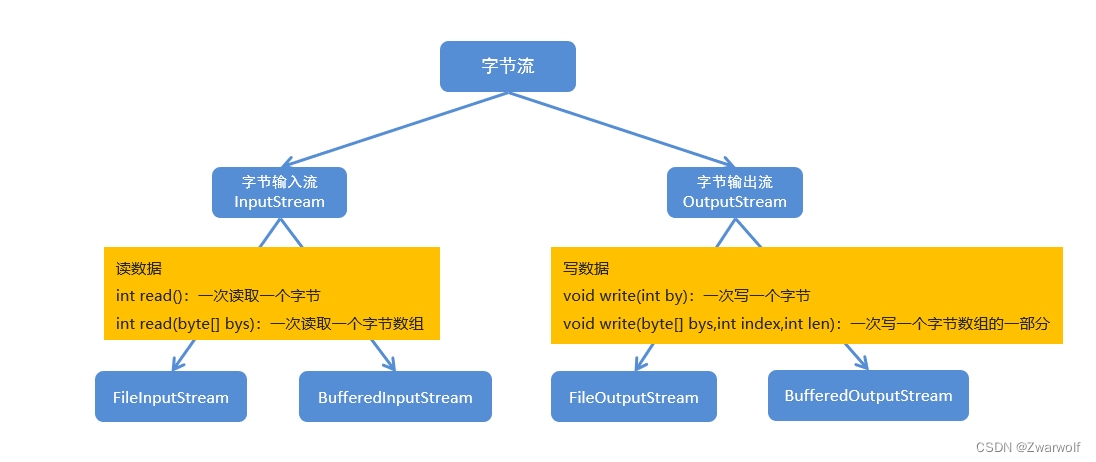
第8章-第4节-Java中字节流的缓冲流
1、缓冲流:属于高级IO流,并不能直接读写数据,需要依赖于基础流。缓冲流的目的是为了提高文件的读写效率?那么是如何提高文件的读写效率的呢? 在内存中设置一个缓冲区,缓冲区的默认大小是8192字节ÿ…...

NULL是什么?
NULL是一个编程术语,通常用于表示一个空值或无效值。在很多编程语言中,NULL用于表示一个变量或指针不引用任何有效的对象或内存位置。 NULL可以看作是一个特殊的值,表示缺少有效的数据或引用。当一个变量被赋予NULL值时,它表示该变…...

FreeRTOS 基础知识
这个基础知识也是非常重要的,那我们要学好 FreeRTOS,这些都是必不可少的。 那么就来看一下本节有哪些内容: 首先呢就是介绍一下什么是任务调度器。接着呢就是任务它拥有哪一些状态了。那这里的内容不多,但是呢都是非常重要的。 …...
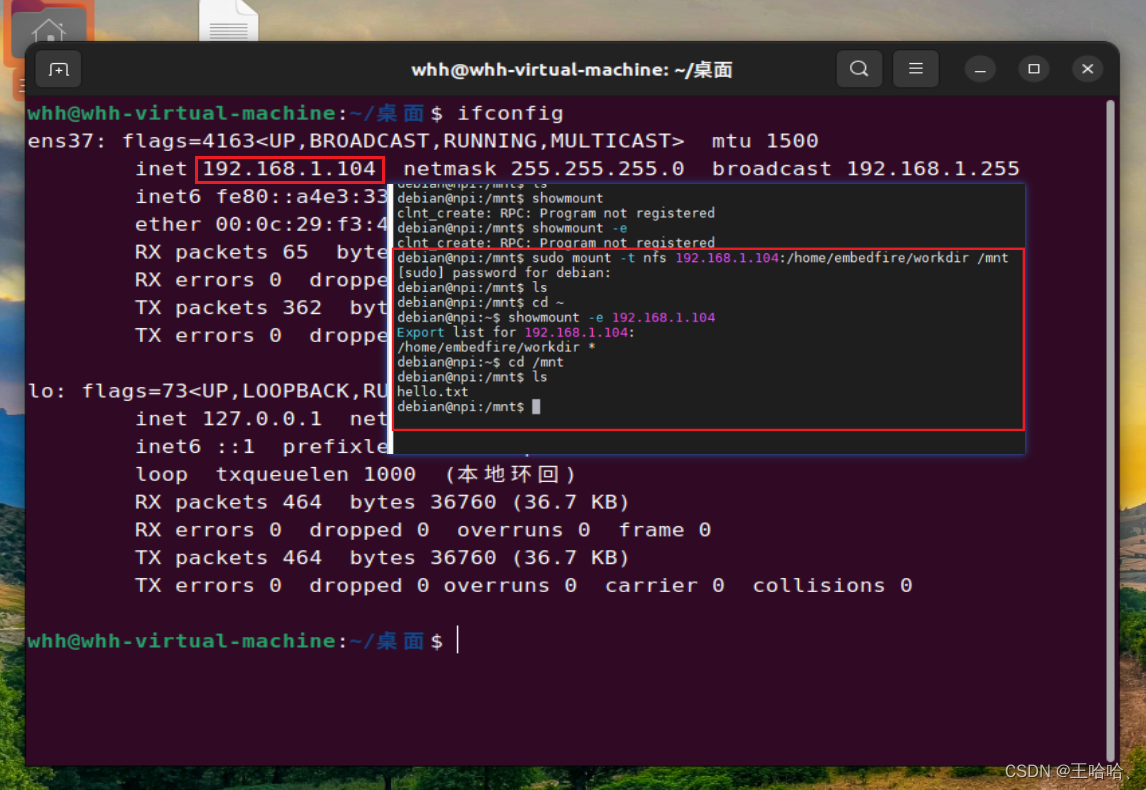
【野火i.MX6NULL开发板】挂载 NFS 网络文件系统
0、前言 参考资料: (误人子弟)《野火 Linux 基础与应用开发实战指南基于 i.MX6ULL 系列》PDF 第22章 参考视频:(成功) https://www.bilibili.com/video/BV1JK4y1t7io?p26&vd_sourcefb8dcae0aee3f1aab…...
方法或展开语法(...)来合并对象,Object.freeze()方法来冻结对象,防止对象被修改)
在JavaScript中,Object.assign()方法或展开语法(...)来合并对象,Object.freeze()方法来冻结对象,防止对象被修改
文章目录 一、Object.freeze()方法来冻结对象,防止对象被修改1、基本使用2、冻结数组2.1、浅冻结2.1、深冻结 3、应用场景4、Vue中使用Object.freeze 二、Object.assign()方法或展开语法(...)来合并对象1、Object.assign()1.1、语法1.2、参数…...
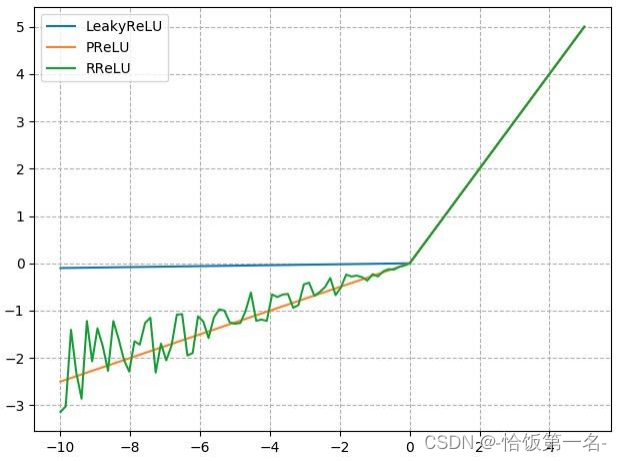
池化、线性、激活函数层
一、池化层 池化运算是深度学习中常用的一种操作,它可以对输入的特征图进行降采样,从而减少特征图的尺寸和参数数量。 池化运算的主要目的是通过“收集”和“总结”输入特征图的信息来提取出主要特征,并且减少对细节的敏感性。在池化运算中…...
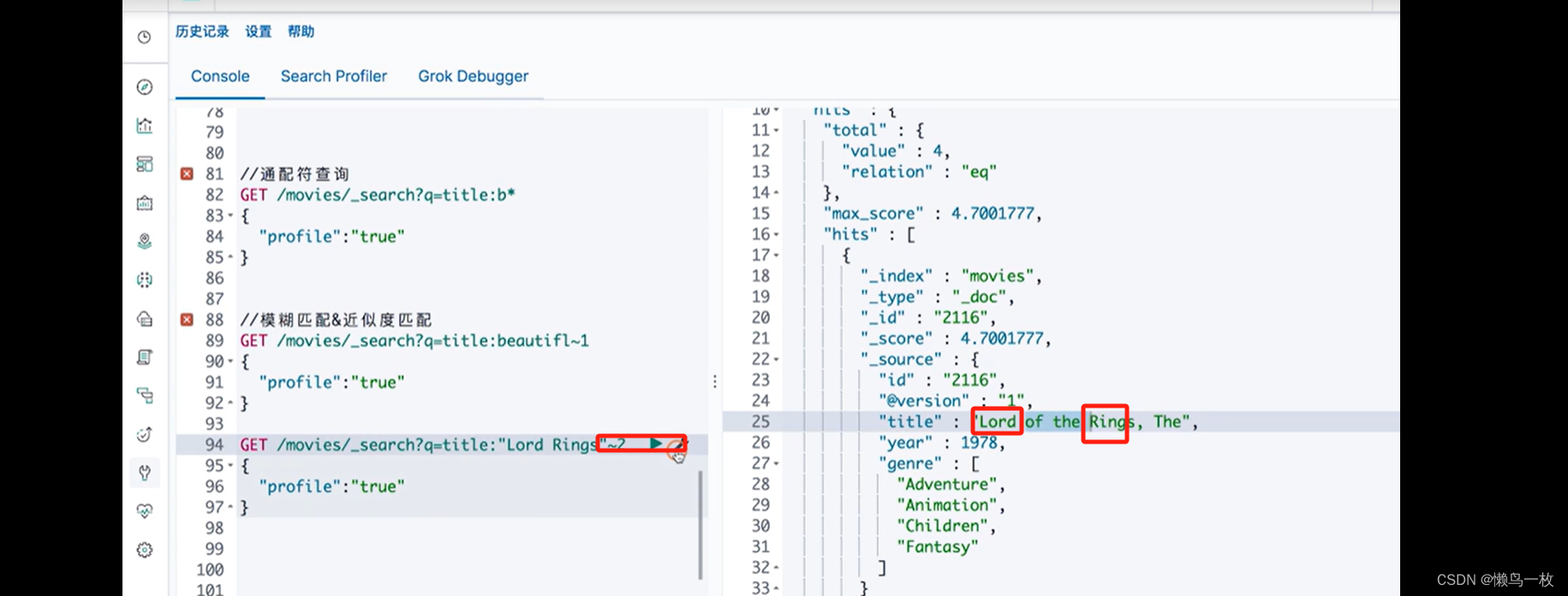
ES-极客学习第二部分ES 入门
基本概念 索引、文档、节点、分片和API json 文档 文档的元数据 需要通过Kibana导入Sample Data的电商数据。具体参考“2.2节-Kibana的安装与界面快速浏览” 索引 kibana 管理ES索引 在系统中找到kibana配置文件(我这里是etc/kibana/kibana.yml) vim /…...

Nodejs软件安装
Nodejs软件安装 一、简介 Node.js 是一个基于 Chrome V8 引擎的 JavaScript 运行环境。 官网:http://nodejs.cn/api/ 我们关注于 node.js 的 npm 功能,NPM 是随同 NodeJS 一起安装的包管理工具,JavaScript-NPM,Java-Maven&…...
Photoshop 2024 (PS2024) v25 直装版 支持win/mac版
Photoshop 2024 提供了多种创意工具,如画笔、铅笔、涂鸦和渐变等,用户可以通过这些工具来创建独特和令人印象深刻的设计效果。增强的云同步:通过 Adobe Creative Cloud,用户可以方便地将他们的工作从一个设备无缝同步到另一个设备…...

ChatGPT绘画生成软件MidTool:智能艺术的新纪元
在人工智能的黄金时代,创新技术不断涌现,改变着我们的生活和工作方式。其中,ChatGPT绘画生成软件MidTool无疑是这一变革浪潮中的佼佼者。它不仅是一个软件,更是一位艺术家,一位智能助手,它的出现预示着智能…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

【FTP】ftp文件传输会丢包吗?批量几百个文件传输,有一些文件没有传输完整,如何解决?
FTP(File Transfer Protocol)本身是一个基于 TCP 的协议,理论上不会丢包。但 FTP 文件传输过程中仍可能出现文件不完整、丢失或损坏的情况,主要原因包括: ✅ 一、FTP传输可能“丢包”或文件不完整的原因 原因描述网络…...
